- Головна
- Готові шкільні презентації
- Презентація на тему «Функції і їх графіки»
Презентація на тему «Функції і їх графіки»
400
Слайд #1
Функції і їх графіки
Слайд #2
Екстремуми функції. Найбільше і найменше значення функції
зміст
Загальні властивості функції
Поняття зворотного функції
Неперервність
елементарні функції
Поняття функції
зміст
Загальні властивості функції
Поняття зворотного функції
Неперервність
елементарні функції
Поняття функції

Слайд #3
Поняття функції
Нехай D і E - непорожні числові множини, а x і y - відповідно їх елементи . Якщо кожному x,D ( x належить безлічі D ) ставиться , відповідно з деяким законом , тільки одне значення y,E , то говорять , що між змінними x і y існує функціональна залежність, і x називають незалежною змінною (або аргументом ) , а y - залежною змінною (або функцією ) .
Символічна запис функції: y = f ( x ) ( x,D , y,E ) . Безліч D називають областю визначення функції і позначають D ( f ) , а безліч E називають областю зміни функції - E ( f ) . Кажуть ще , що функція f відображає безліч D на безлічі E.
Нехай D і E - непорожні числові множини, а x і y - відповідно їх елементи . Якщо кожному x,D ( x належить безлічі D ) ставиться , відповідно з деяким законом , тільки одне значення y,E , то говорять , що між змінними x і y існує функціональна залежність, і x називають незалежною змінною (або аргументом ) , а y - залежною змінною (або функцією ) .
Символічна запис функції: y = f ( x ) ( x,D , y,E ) . Безліч D називають областю визначення функції і позначають D ( f ) , а безліч E називають областю зміни функції - E ( f ) . Кажуть ще , що функція f відображає безліч D на безлічі E.

Слайд #4
Загальні властивості функції
Парність і непарність
Періодичність
Нулі функції
Проміжки знакосталості
Парність і непарність
Періодичність
Нулі функції
Проміжки знакосталості

Слайд #5
Парність і непарність
Визначення: Функція y = f (x) називається парною, якщо для будь-якого значення x, взятого з області визначення функції, значення-x також належить області визначення і виконується рівність f (-x) = f (x).
Приклади парних функцій:
y = x2; y = x2 + 5; y =-3x2 + 1; y = ½ x ½; y = 3.
(y = x2; y (1) = 12 = 1; y (-1) = (-1) 2 = 1; y (1) = y (-1)).
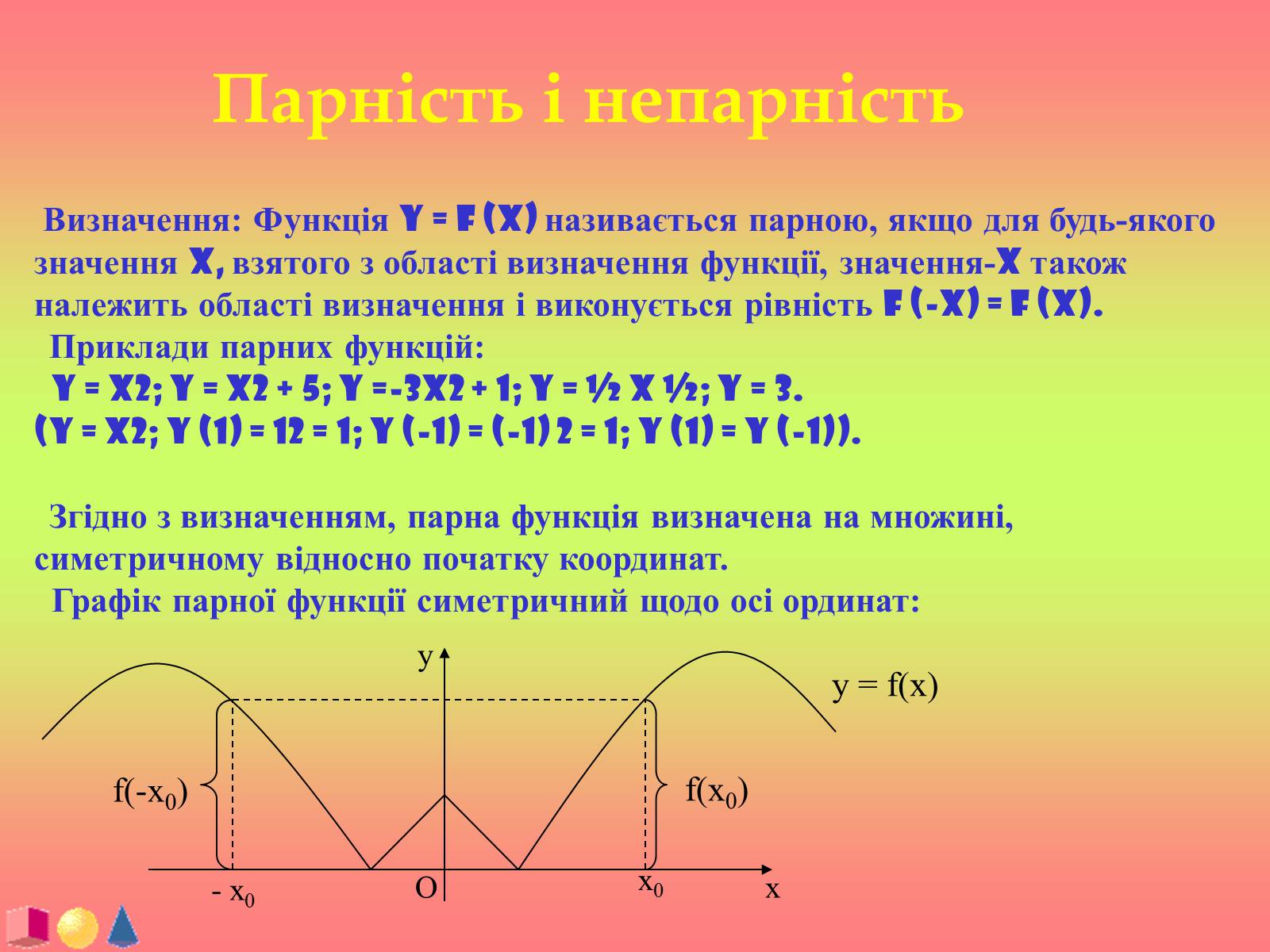
Згідно з визначенням, парна функція визначена на множині, симетричному відносно початку координат.
Графік парної функції симетричний щодо осі ординат:
y
x
O
x0
- x0
f(x0)
f(-x0)
y = f(x)
Визначення: Функція y = f (x) називається парною, якщо для будь-якого значення x, взятого з області визначення функції, значення-x також належить області визначення і виконується рівність f (-x) = f (x).
Приклади парних функцій:
y = x2; y = x2 + 5; y =-3x2 + 1; y = ½ x ½; y = 3.
(y = x2; y (1) = 12 = 1; y (-1) = (-1) 2 = 1; y (1) = y (-1)).
Згідно з визначенням, парна функція визначена на множині, симетричному відносно початку координат.
Графік парної функції симетричний щодо осі ординат:
y
x
O
x0
- x0
f(x0)
f(-x0)
y = f(x)
Слайд #6
Визначення: Функція y = f (x) називається непарною, якщо для будь-якого значення x, взятого з області визначення функції, значення-x також належить області визначення і виконується рівність f (-x) =-f (x).
Приклади непарних функцій:
y = x3; y = x3 + x.
(y = x3; y (1) = 13 = 1; y (-1) = (-1) 3 = -1; y (-1) =-y (1)).
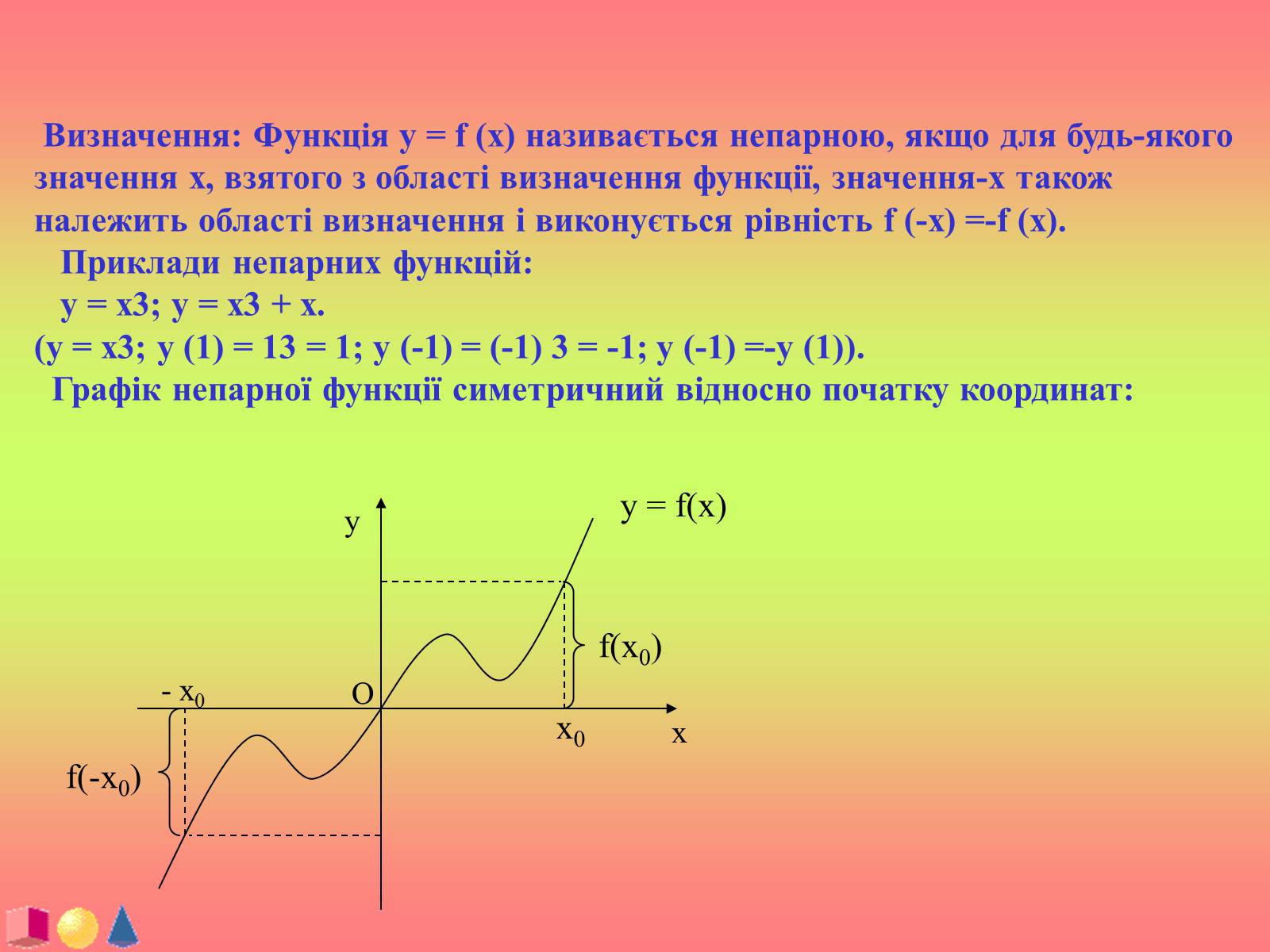
Графік непарної функції симетричний відносно початку координат:
y
x
x0
- x0
f(x0)
f(-x0)
O
y = f(x)
Приклади непарних функцій:
y = x3; y = x3 + x.
(y = x3; y (1) = 13 = 1; y (-1) = (-1) 3 = -1; y (-1) =-y (1)).
Графік непарної функції симетричний відносно початку координат:
y
x
x0
- x0
f(x0)
f(-x0)
O
y = f(x)
Слайд #7
При побудові графіків парній і непарній функції досить побудувати тільки праву гілку графіка для позитивних значень аргументу. Ліва галузь добудовується симетрично відносно початку координат для непарної функції і відносно осі ординат для парної функції.
Твір двох парних або двох непарних функцій являє собою парну функцію, а твір парній і непарній функцій - непарну функцію.
Звичайно, більшість функцій не є ні парними, ні непарними.
приклад:
y = x3 + x2
y(-1) = (-1)3 + (-1)2 = -1 + 1 = 0
y(1) = (1)3 + (1)2 = 1 + 1 = 2
Твір двох парних або двох непарних функцій являє собою парну функцію, а твір парній і непарній функцій - непарну функцію.
Звичайно, більшість функцій не є ні парними, ні непарними.
приклад:
y = x3 + x2
y(-1) = (-1)3 + (-1)2 = -1 + 1 = 0
y(1) = (1)3 + (1)2 = 1 + 1 = 2

Слайд #8
Нулі функції
Визначення: Нулем функції називається таке дійсне значення x, при якому значення функції дорівнює нулю.
x
y
O
x1
x3
x2
y = f(x)
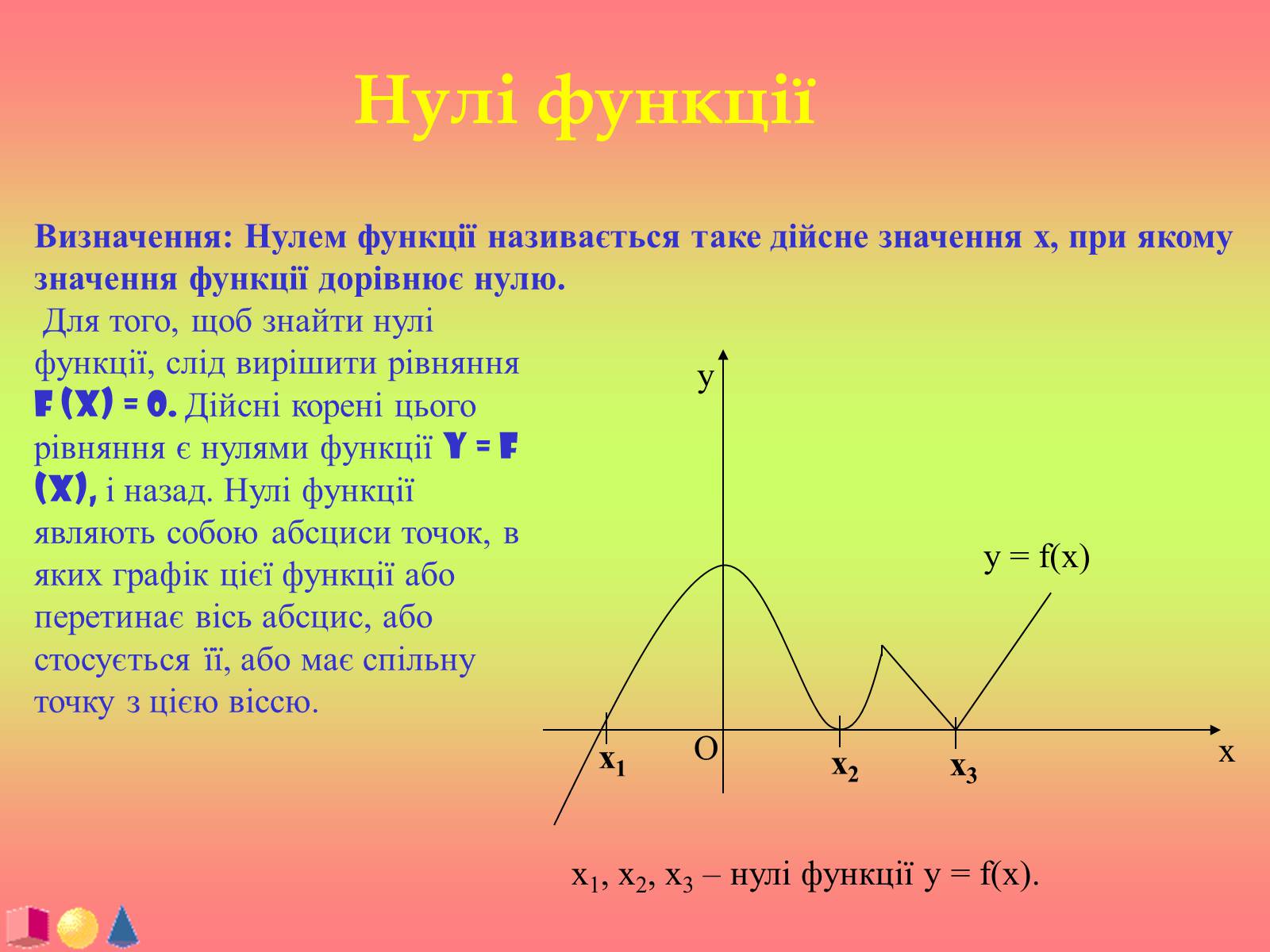
Для того, щоб знайти нулі функції, слід вирішити рівняння f (x) = 0. Дійсні корені цього рівняння є нулями функції y = f (x), і назад. Нулі функції являють собою абсциси точок, в яких графік цієї функції або перетинає вісь абсцис, або стосується її, або має спільну точку з цією віссю.
х1, х2, х3 – нулі функції у = f(x).
Визначення: Нулем функції називається таке дійсне значення x, при якому значення функції дорівнює нулю.
x
y
O
x1
x3
x2
y = f(x)
Для того, щоб знайти нулі функції, слід вирішити рівняння f (x) = 0. Дійсні корені цього рівняння є нулями функції y = f (x), і назад. Нулі функції являють собою абсциси точок, в яких графік цієї функції або перетинає вісь абсцис, або стосується її, або має спільну точку з цією віссю.
х1, х2, х3 – нулі функції у = f(x).
Слайд #9
Екстремуми функції. Найбільше і найменше значення функції
Точка x0 називається точкою максимуму (точкою мінімуму) для функції f (x), якщо значення в цій точці більше (менше), ніж значення функції в найближчих сусідніх точках.
для позначення максимуму і мінімуму існує загальний термін «екстремум» (від латинського «крайній»).
Точка x0 називається точкою максимуму (точкою мінімуму) для функції f (x), якщо значення в цій точці більше (менше), ніж значення функції в найближчих сусідніх точках.
для позначення максимуму і мінімуму існує загальний термін «екстремум» (від латинського «крайній»).

Слайд #10
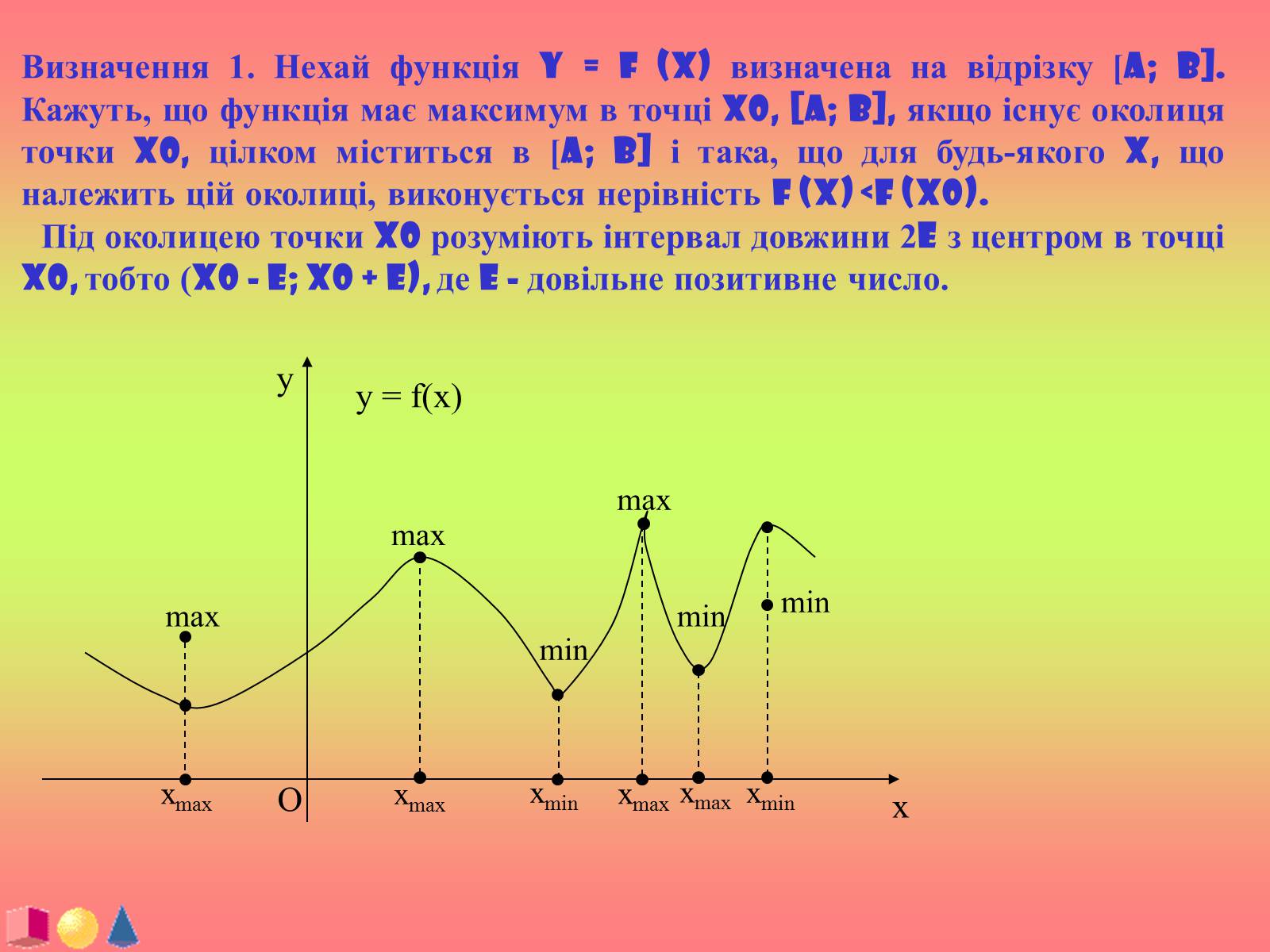
Визначення 1. Нехай функція y = f (x) визначена на відрізку [a; b]. Кажуть, що функція має максимум в точці x0, [a; b], якщо існує околиця точки x0, цілком міститься в [a; b] і така, що для будь-якого x, що належить цій околиці, виконується нерівність f (x) Під околицею точки x0 розуміють інтервал довжини 2e з центром в точці x0, тобто (x0 - e; x0 + e), де e - довільне позитивне число.
y
x
O
y = f(x)
max
max
max
min
min
min
xmax
xmax
xmax
xmax
xmin
xmin
y
x
O
y = f(x)
max
max
max
min
min
min
xmax
xmax
xmax
xmax
xmin
xmin
Слайд #11
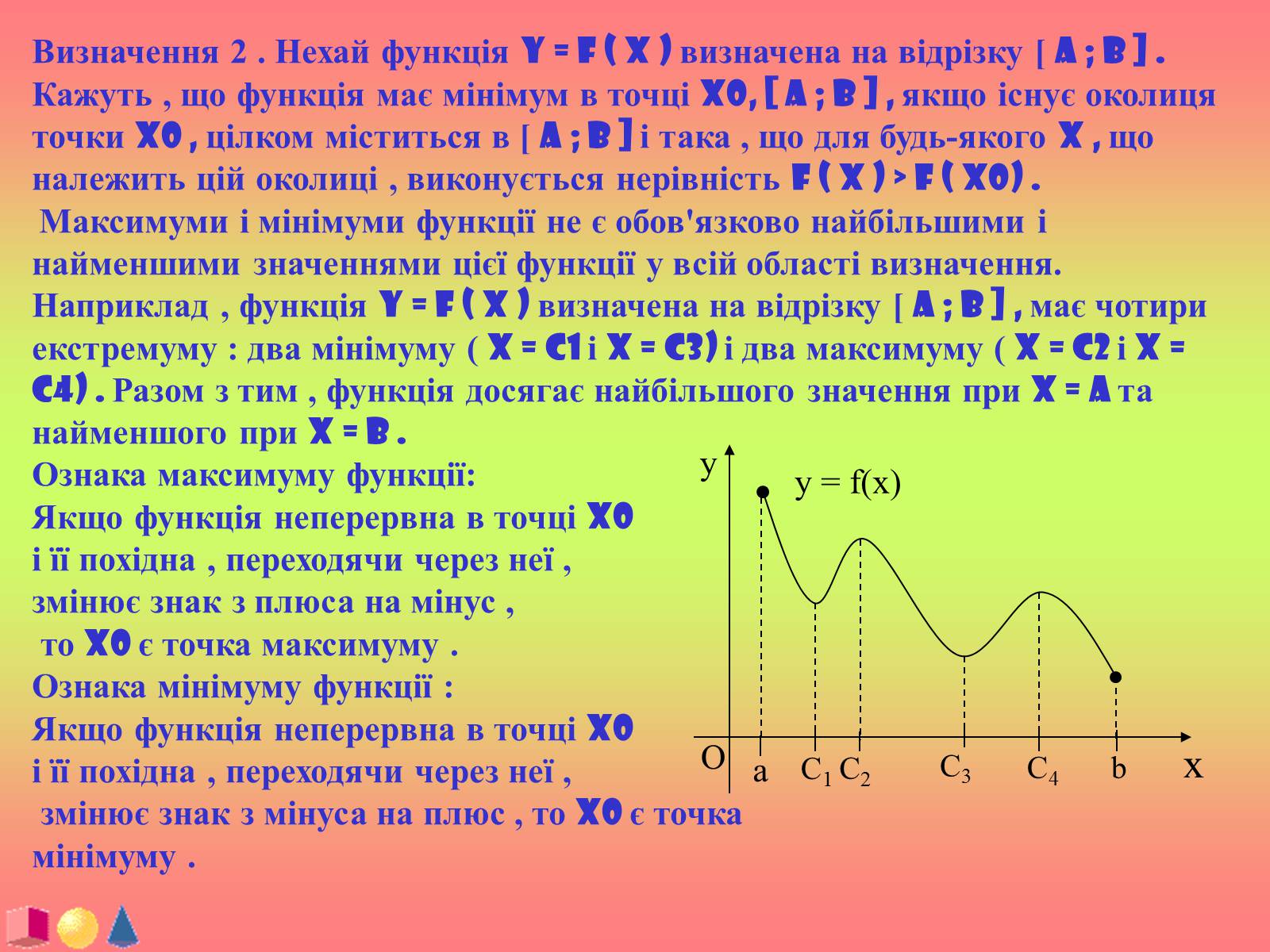
Визначення 2 . Нехай функція y = f ( x ) визначена на відрізку [ a ; b ] . Кажуть , що функція має мінімум в точці x0, [ a ; b ] , якщо існує околиця точки x0 , цілком міститься в [ a ; b ] і така , що для будь-якого x , що належить цій околиці , виконується нерівність f ( x ) > f ( x0) .
Максимуми і мінімуми функції не є обов'язково найбільшими і найменшими значеннями цієї функції у всій області визначення. Наприклад , функція y = f ( x ) визначена на відрізку [ a ; b ] , має чотири екстремуму : два мінімуму ( x = C1 і x = C3) і два максимуму ( x = C2 і x = C4) . Разом з тим , функція досягає найбільшого значення при x = a та найменшого при x = b .
Ознака максимуму функції:
Якщо функція неперервна в точці x0
і її похідна , переходячи через неї ,
змінює знак з плюса на мінус ,
то x0 є точка максимуму .
Ознака мінімуму функції :
Якщо функція неперервна в точці x0
і її похідна , переходячи через неї ,
змінює знак з мінуса на плюс , то x0 є точка
мінімуму .
O
y
x
a
b
C1
C2
C3
C4
y = f(x)
Максимуми і мінімуми функції не є обов'язково найбільшими і найменшими значеннями цієї функції у всій області визначення. Наприклад , функція y = f ( x ) визначена на відрізку [ a ; b ] , має чотири екстремуму : два мінімуму ( x = C1 і x = C3) і два максимуму ( x = C2 і x = C4) . Разом з тим , функція досягає найбільшого значення при x = a та найменшого при x = b .
Ознака максимуму функції:
Якщо функція неперервна в точці x0
і її похідна , переходячи через неї ,
змінює знак з плюса на мінус ,
то x0 є точка максимуму .
Ознака мінімуму функції :
Якщо функція неперервна в точці x0
і її похідна , переходячи через неї ,
змінює знак з мінуса на плюс , то x0 є точка
мінімуму .
O
y
x
a
b
C1
C2
C3
C4
y = f(x)
Слайд #12
Неперервність
Функція y = f ( x ) називається безперервної на проміжку , якщо вона визначена на цьому проміжку і неперервна в кожній точці проміжку .
Геометрична безперервність функції на проміжку означає , що графік цієї функції на даному проміжку зображений суцільною лінією без стрибків і розривів . При цьому малій зміні аргументу відповідає мале зміна функції .
Якщо при x = a функція y = f ( x ) існує в околиці цієї точки , але в самій точці x = a не виконується умова безперервності , кажуть , що точка x = a є точка розриву функції . У самій точці x = a функція може існувати , а може і не існувати.
О
у
х
y = f(x)
а
b
О
х
у
y = f(x)
а
О
х
у
y = f(x)
а
Функція y = f ( x ) називається безперервної на проміжку , якщо вона визначена на цьому проміжку і неперервна в кожній точці проміжку .
Геометрична безперервність функції на проміжку означає , що графік цієї функції на даному проміжку зображений суцільною лінією без стрибків і розривів . При цьому малій зміні аргументу відповідає мале зміна функції .
Якщо при x = a функція y = f ( x ) існує в околиці цієї точки , але в самій точці x = a не виконується умова безперервності , кажуть , що точка x = a є точка розриву функції . У самій точці x = a функція може існувати , а може і не існувати.
О
у
х
y = f(x)
а
b
О
х
у
y = f(x)
а
О
х
у
y = f(x)
а

Слайд #13
елементарні функції
лінійна
квадратична
степенева
лінійна
квадратична
степенева

Слайд #14
Лінійна функція
Визначення: Функція виду y = kx + b, де k і b деякі числа, називається лінійною функцією.
1. Якщо k = 0, тоді y = b.
Ця функція визначена на множині R і для кожного X приймає одне і те ж значення, рівне b.
Графіком є пряма, паралельна осі Оx і віддалена від неї на ½ b ½ одиниць вгору, якщо b> 0, і вниз, якщо b <0; якщо b = 0, то пряма співпадає з віссю Ox.
y
x
O
b
b
y = b; b > 0
y = b; b < 0
Визначення: Функція виду y = kx + b, де k і b деякі числа, називається лінійною функцією.
1. Якщо k = 0, тоді y = b.
Ця функція визначена на множині R і для кожного X приймає одне і те ж значення, рівне b.
Графіком є пряма, паралельна осі Оx і віддалена від неї на ½ b ½ одиниць вгору, якщо b> 0, і вниз, якщо b <0; якщо b = 0, то пряма співпадає з віссю Ox.
y
x
O
b
b
y = b; b > 0
y = b; b < 0

Слайд #15
2. Якщо b = 0, то y = kx.
Лінійна функція виду y = kx називається прямою пропорційністю. Вона визначена на безлічі R. Функція є монотонно зростаючою, якщо k> 0, і монотонно спадною, якщо k <0. Графіком функції є пряма, що проходить через початок координат. При k> 0 точки графіка належать I і III координатних чвертях. При k <0 точки графіка належать II і IV координатних чвертях.
O
y
x
y = kx
k > 0
O
y
x
y = kx
k < 0
Лінійна функція виду y = kx називається прямою пропорційністю. Вона визначена на безлічі R. Функція є монотонно зростаючою, якщо k> 0, і монотонно спадною, якщо k <0. Графіком функції є пряма, що проходить через початок координат. При k> 0 точки графіка належать I і III координатних чвертях. При k <0 точки графіка належать II і IV координатних чвертях.
O
y
x
y = kx
k > 0
O
y
x
y = kx
k < 0

Слайд #16
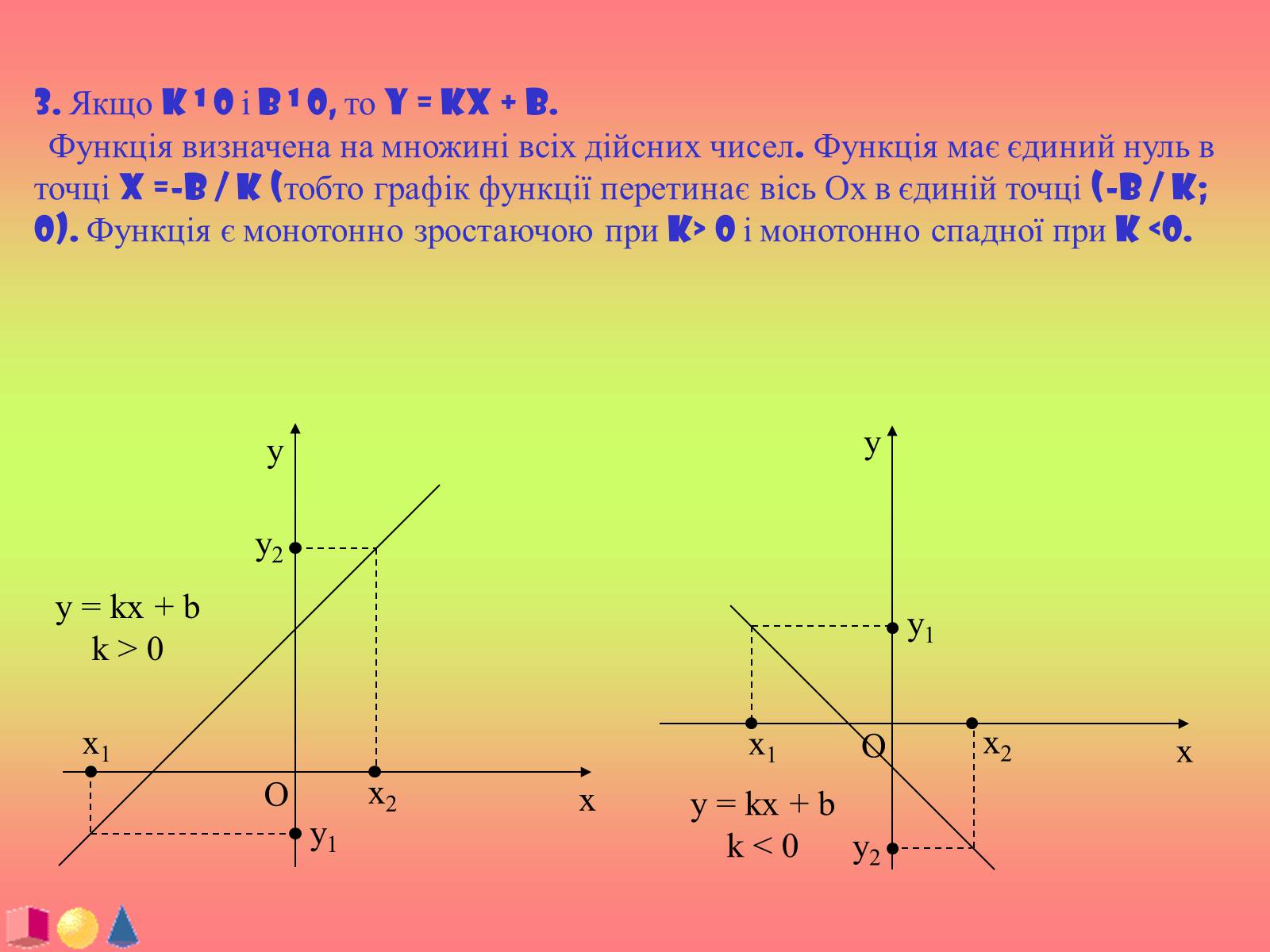
3. Якщо k ¹ 0 і b ¹ 0, то y = kx + b.
Функція визначена на множині всіх дійсних чисел. Функція має єдиний нуль в точці x =-b / k (тобто графік функції перетинає вісь Ох в єдиній точці (-b / k; 0). Функція є монотонно зростаючою при k> 0 і монотонно спадної при k <0.
O
y
x
x1
x2
y1
y2
y = kx + b
k > 0
O
y
x
x1
x2
y1
y2
y = kx + b
k < 0
Функція визначена на множині всіх дійсних чисел. Функція має єдиний нуль в точці x =-b / k (тобто графік функції перетинає вісь Ох в єдиній точці (-b / k; 0). Функція є монотонно зростаючою при k> 0 і монотонно спадної при k <0.
O
y
x
x1
x2
y1
y2
y = kx + b
k > 0
O
y
x
x1
x2
y1
y2
y = kx + b
k < 0
Слайд #17
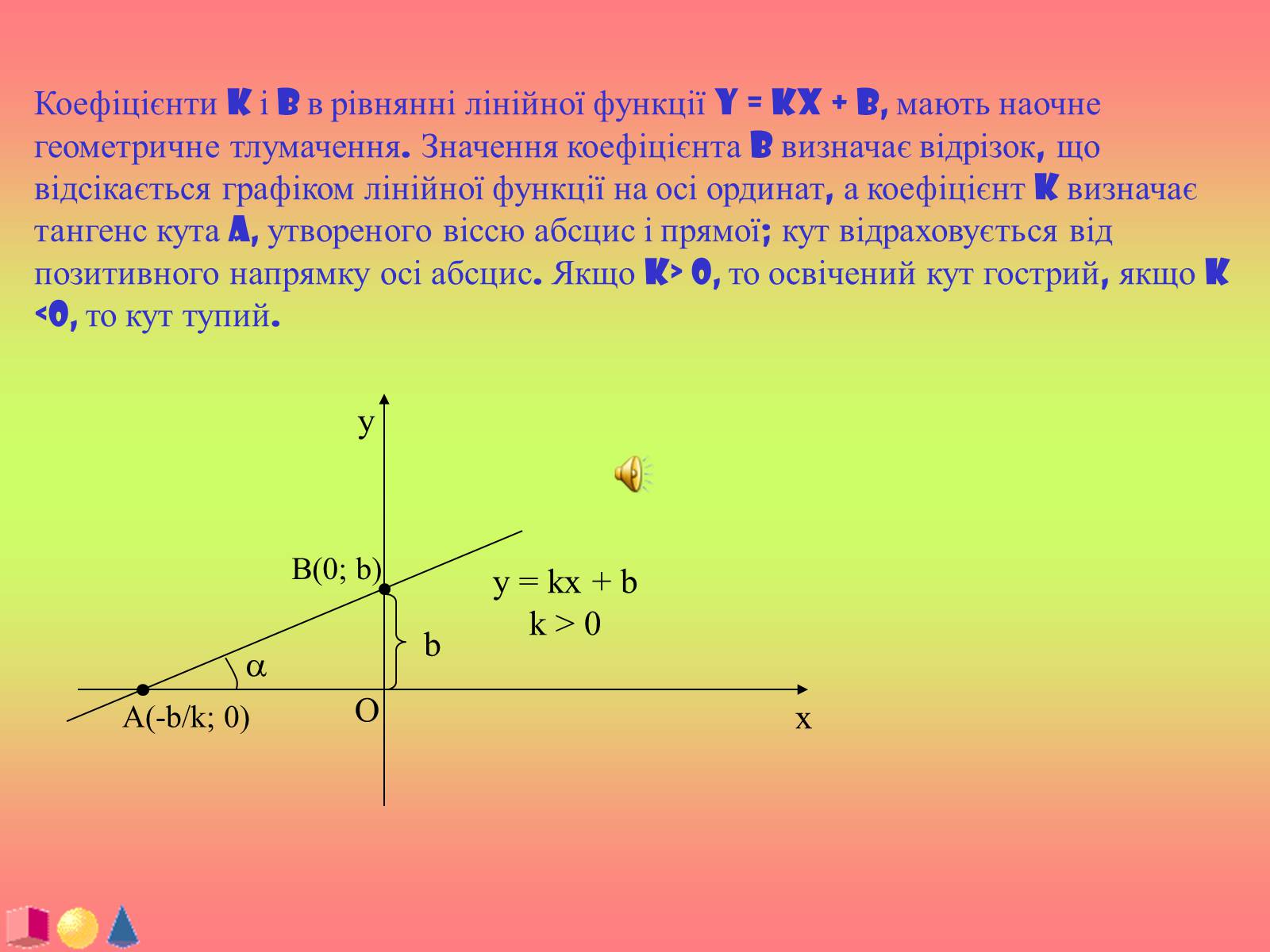
Коефіцієнти k і b в рівнянні лінійної функції y = kx + b, мають наочне геометричне тлумачення. Значення коефіцієнта b визначає відрізок, що відсікається графіком лінійної функції на осі ординат, а коефіцієнт k визначає тангенс кута a, утвореного віссю абсцис і прямої; кут відраховується від позитивного напрямку осі абсцис. Якщо k> 0, то освічений кут гострий, якщо k <0, то кут тупий.
a
О
y
x
b
B(0; b)
y = kx + b
k > 0
A(-b/k; 0)
a
О
y
x
b
B(0; b)
y = kx + b
k > 0
A(-b/k; 0)
Слайд #18
Квадратична функція
Визначення: Функція виду y = ax2 + bx + c, де a, b, c - деякі числа, a ¹ 0, називається квадратичною.
1. Функція виду y = x2 - найпростіша квадратична функція. Це парна функція, у якої D = (- ∞; + ∞), а E = [0; + ∞). При x> 0 вона зростаюча, а при x <0 - спадна. Її графік називається параболою. Графік проходить через початок координат, симетричний щодо осі ординат, гілки параболи спрямовані вгору.
y
x
O
1
-1
1
y = x2
Визначення: Функція виду y = ax2 + bx + c, де a, b, c - деякі числа, a ¹ 0, називається квадратичною.
1. Функція виду y = x2 - найпростіша квадратична функція. Це парна функція, у якої D = (- ∞; + ∞), а E = [0; + ∞). При x> 0 вона зростаюча, а при x <0 - спадна. Її графік називається параболою. Графік проходить через початок координат, симетричний щодо осі ординат, гілки параболи спрямовані вгору.
y
x
O
1
-1
1
y = x2

Слайд #19
2. Квадратична функція виду y = ax2 також парна, необмежена, визначена для всіх дійсних x. Її графік також парабола, що проходить через початок координат і симетрична щодо осі ординат. Але при a> 0 гілки її спрямовані вгору і E = [0; + ∞), а при a <0 гілки спрямовані вниз і E = (- ∞; 0). Чим менше абсолютна величина a, тим далі відходять гілки параболи від осі ординат, тим «ширше» вона. Чим більше абсолютна величина a, тим щільніше гілки параболи притиснуті до осі ординат, тим «вже» вона.
y
x
O
1
-1
1
y = аx2
a > 0; ½a½ > 1
y
x
O
1
-1
-1
y = ax2
a < 0; ½a½ < 1
y
x
O
1
-1
1
y = аx2
a > 0; ½a½ > 1
y
x
O
1
-1
-1
y = ax2
a < 0; ½a½ < 1

Слайд #20
3 . Квадратична функція загального вигляду y = ax2 + bx + c також парна , необмежена , визначена для всіх дійсних x . Її графік - парабола , симетрична відносно прямої x = x0 (x0 - абсциса вершини параболи ) , паралельної осі ординат . Якщо a > 0 , то її гілки спрямовані вгору і E = [ y0 ; + ∞ ) або вниз при a <0 і тоді E = ( - ∞ ; y0) , де y0 - ордината вершини параболи . Тільки вершина цієї параболи знаходиться не на початку координат , а в точці ( - b / 2a ; ( 4ac - b2) / 4a ) . Парабола перетинає вісь ординат у точці (0; c ) . Якщо дискримінант квадратного тричлена ax2 + bx + c негативний, тобто B2 - 4ac <0 , то графік функції y = ax2 + bx + c не перетинає вісь абсцис .
y = ax2 + bx +c
a < 0
y
O
x
-b/2a
(0; c)
y = ax2 + bx +c
a < 0
y
O
x
-b/2a
(0; c)

Слайд #21
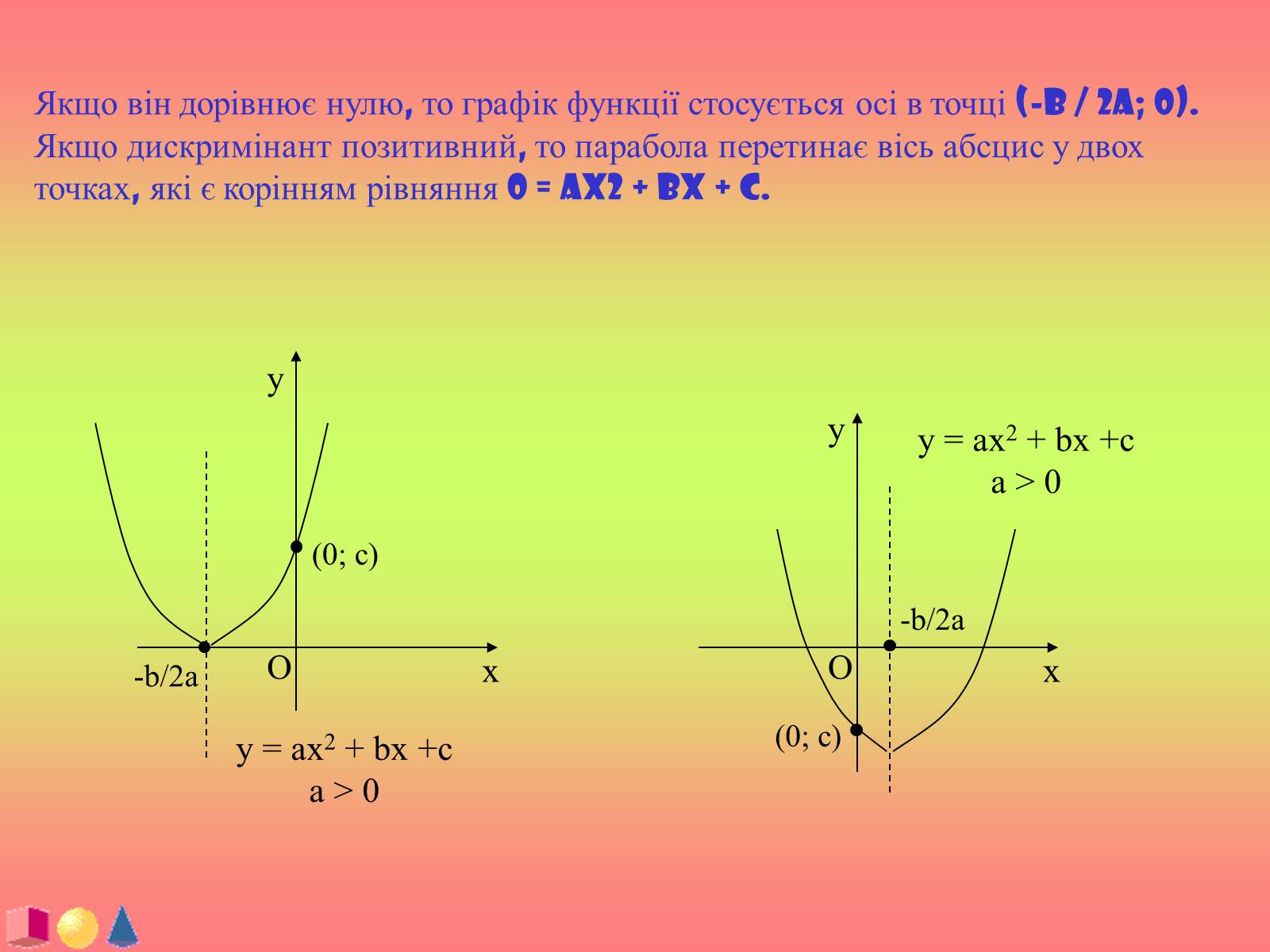
Якщо він дорівнює нулю, то графік функції стосується осі в точці (-b / 2a; 0). Якщо дискримінант позитивний, то парабола перетинає вісь абсцис у двох точках, які є корінням рівняння 0 = ax2 + bx + c.
O
y
x
-b/2a
(0; c)
y = ax2 + bx +c
a > 0
O
y
x
-b/2a
(0; c)
y = ax2 + bx +c
a > 0
O
y
x
-b/2a
(0; c)
y = ax2 + bx +c
a > 0
O
y
x
-b/2a
(0; c)
y = ax2 + bx +c
a > 0
Слайд #22
Степенева функція
Визначення: Функція , задана формулою y = xn , називається статечної .
1 . При n , рівному 1 ; 2 ; -1 , маємо відповідно функції y = x , y = x2 ; y = -1 / x , вже розглянуті раніше .
2 . Якщо n - число ціле і парне , то функція y = xn - парна ; при непарному n вона непарна . При позитивних n ця функція визначена для всіх дійсних значень аргументу x , при негативних n вона визначена для всіх x , крім x = 0.
При будь-якому n ¹ 0 статечна функція необмежена , графік кожній з них проходить через точку ( 1 ; 1).
Якщо n - число ірраціональне , то функція y = xn визначена тільки для позитивних значень аргументу x або для невід'ємних x , якщо n > 0.
Визначення: Функція , задана формулою y = xn , називається статечної .
1 . При n , рівному 1 ; 2 ; -1 , маємо відповідно функції y = x , y = x2 ; y = -1 / x , вже розглянуті раніше .
2 . Якщо n - число ціле і парне , то функція y = xn - парна ; при непарному n вона непарна . При позитивних n ця функція визначена для всіх дійсних значень аргументу x , при негативних n вона визначена для всіх x , крім x = 0.
При будь-якому n ¹ 0 статечна функція необмежена , графік кожній з них проходить через точку ( 1 ; 1).
Якщо n - число ірраціональне , то функція y = xn визначена тільки для позитивних значень аргументу x або для невід'ємних x , якщо n > 0.
