- Головна
- Готові шкільні презентації
- Презентація на тему «Двогранний кут»
Презентація на тему «Двогранний кут»
1583
Слайд #1
Двогранний кут

Слайд #2
На наступних слайдах ваш конспект, який повинен бути як класна робота; будуть завдання класної роботи, які вам потрібно переписати: деякі вже вирішені мною, а деякі вам потрібно вирішити самостійно за зразком (вони виділені маркером). Всі завдання повинні йти у тому порядку, у якому я їх вам даю (і самостійні теж).

Слайд #3
03.11.14
Класна робота
Тема: Двогранні кути. Лінійний кут двогранного кута
Мета:
Сформувати поняття двогранного та многогранного кутів,
забезпечити формування умінь і навичок учнів будувати двогранні
та тригранні кути та розв'язування задач із використанням
та логічне мислення в учнів. Виховувати самостійність та
многогранних кутів. Розвивати просторову уяву, спостережливість
наполегливість у дітей під час уроку.
Класна робота
Тема: Двогранні кути. Лінійний кут двогранного кута
Мета:
Сформувати поняття двогранного та многогранного кутів,
забезпечити формування умінь і навичок учнів будувати двогранні
та тригранні кути та розв'язування задач із використанням
та логічне мислення в учнів. Виховувати самостійність та
многогранних кутів. Розвивати просторову уяву, спостережливість
наполегливість у дітей під час уроку.

Слайд #4
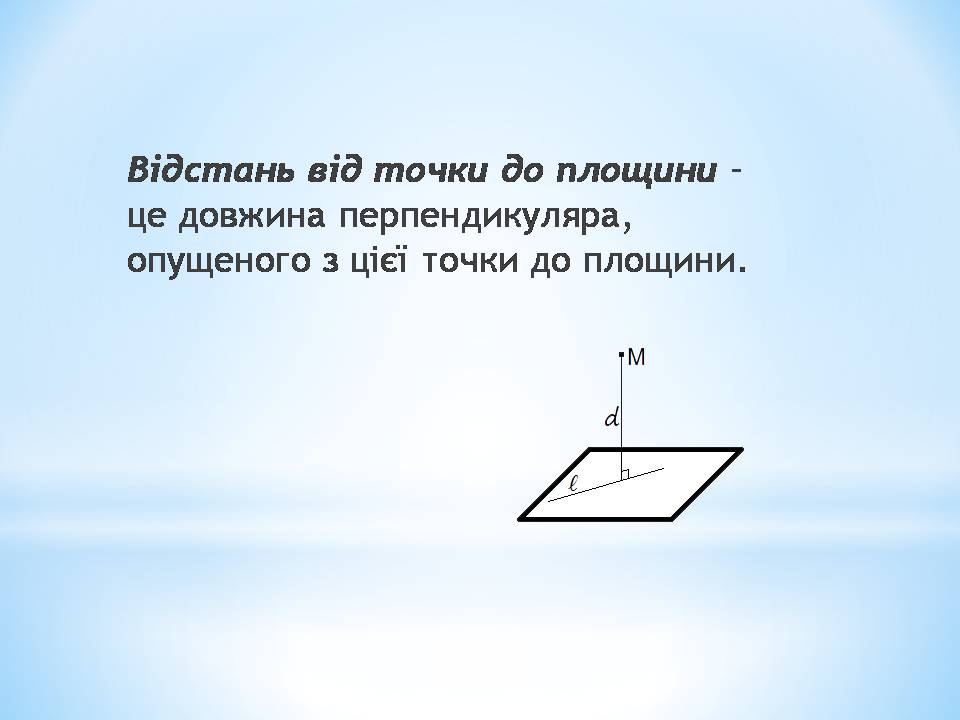
Відстань від точки до площини – це довжина перпендикуляра, опущеного з цієї точки до площини.
Слайд #5
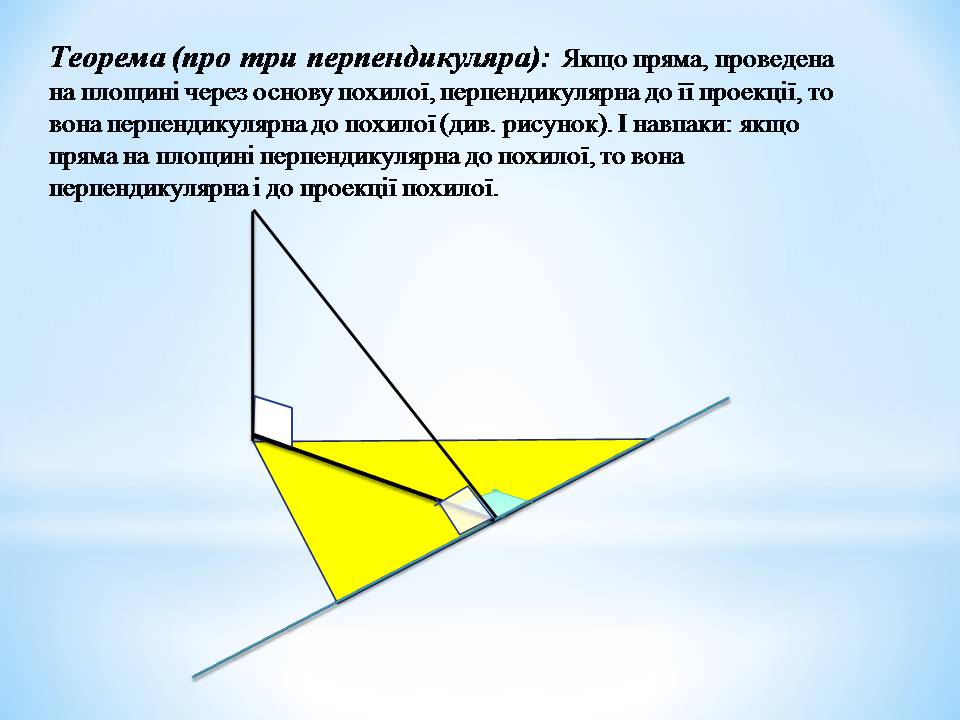
Теорема (про три перпендикуляра): Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до похилої (див. рисунок). І навпаки: якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.
Слайд #6
α
β
м
N
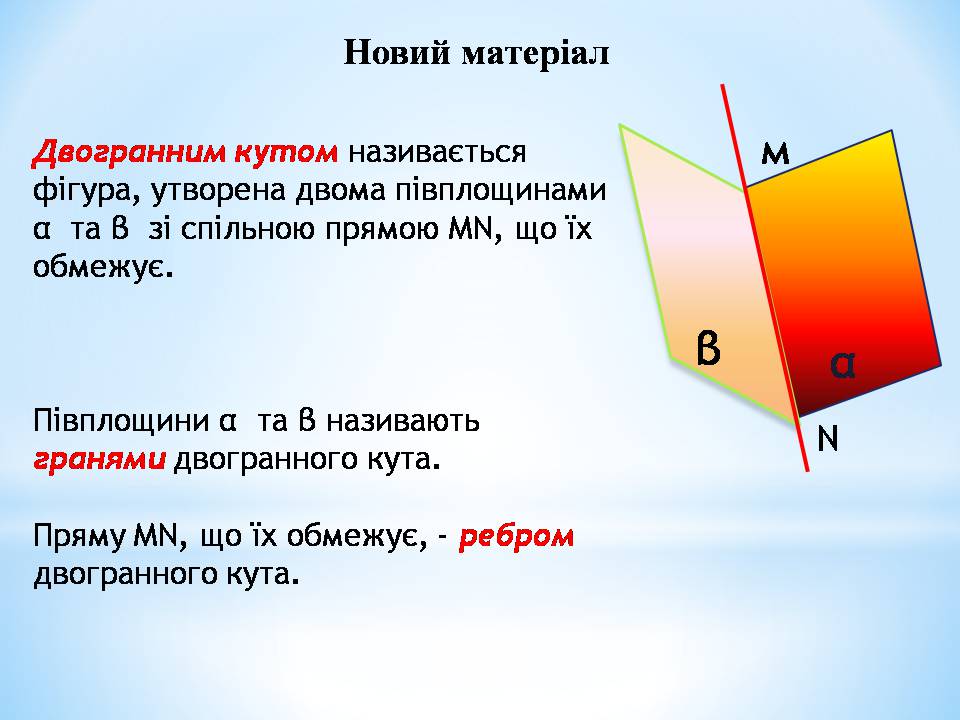
Двогранним кутом називається фігура, утворена двома півплощинами α та β зі спільною прямою МN, що їх обмежує.
Півплощини α та β називають гранями двогранного кута.
Пряму МN, що їх обмежує, - ребром двогранного кута.
Новий матеріал
β
м
N
Двогранним кутом називається фігура, утворена двома півплощинами α та β зі спільною прямою МN, що їх обмежує.
Півплощини α та β називають гранями двогранного кута.
Пряму МN, що їх обмежує, - ребром двогранного кута.
Новий матеріал
Слайд #7
α
β
м
N
Двогранним кутом називається фігура, утворена двома півплощинами α та β зі спільною прямою МN, що їх обмежує.
Півплощини α та β називають гранями двогранного кута.
Пряму МN, що їх обмежує, - ребром двогранного кута.
Новий матеріал
β
м
N
Двогранним кутом називається фігура, утворена двома півплощинами α та β зі спільною прямою МN, що їх обмежує.
Півплощини α та β називають гранями двогранного кута.
Пряму МN, що їх обмежує, - ребром двогранного кута.
Новий матеріал

Слайд #8
A
D
C
H
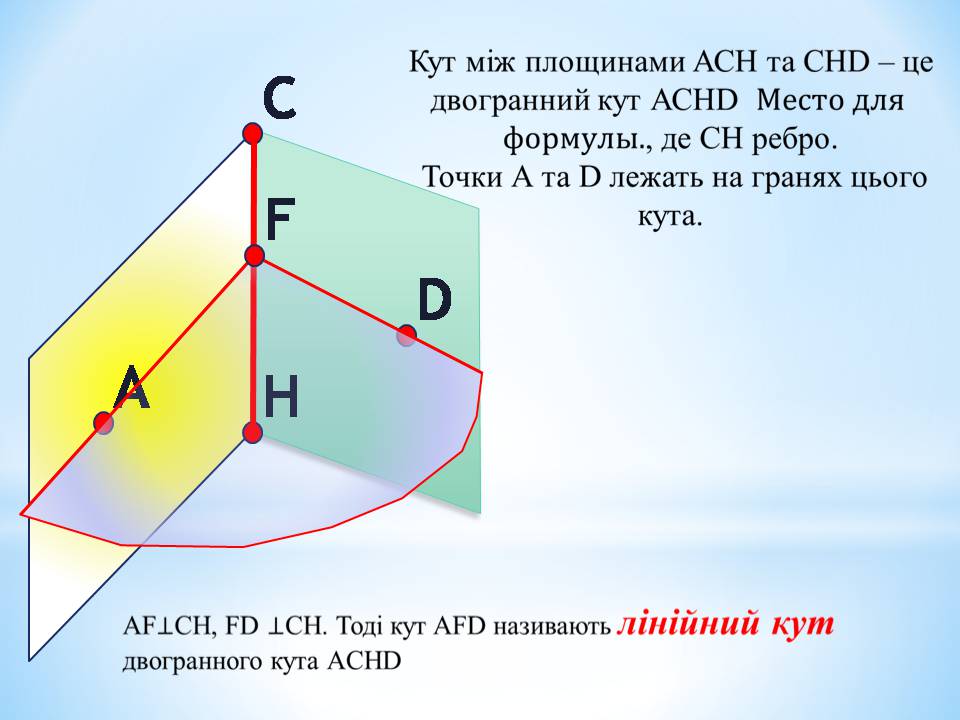
Кут міжплощинами АСН та СНD – цедвогранний кут АСНDМесто для формулы., де СН ребро.
Точки А та D лежать на гранях цього кута.
F
AFCH, FDCH. Тоді кут AFDназиваютьлінійнийкут двогранного кута АCHD
D
C
H
Кут міжплощинами АСН та СНD – цедвогранний кут АСНDМесто для формулы., де СН ребро.
Точки А та D лежать на гранях цього кута.
F
AFCH, FDCH. Тоді кут AFDназиваютьлінійнийкут двогранного кута АCHD
Слайд #9
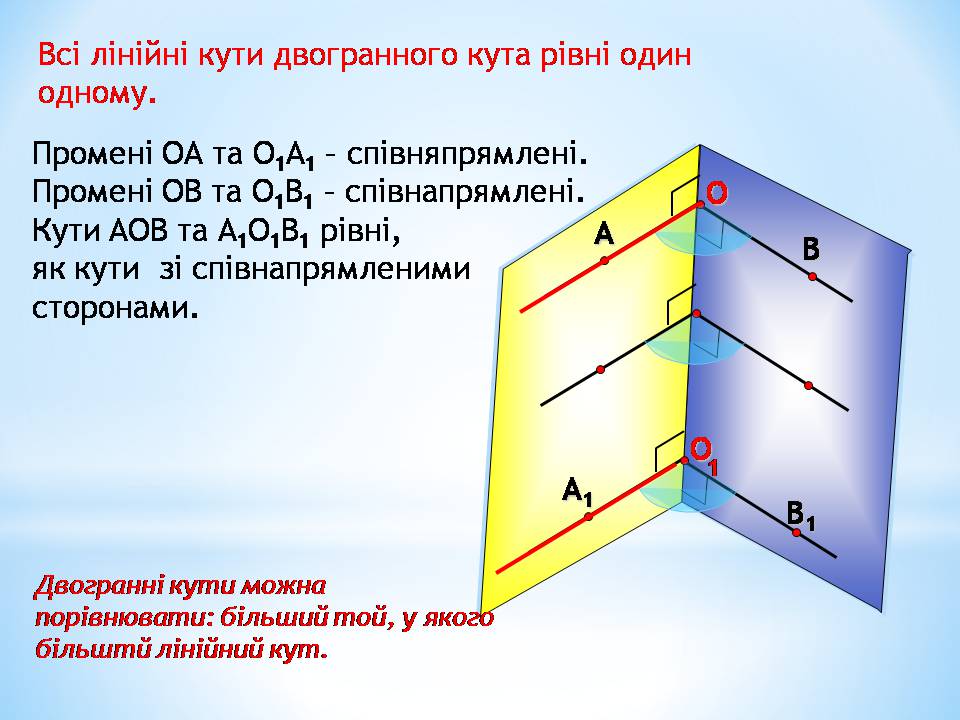
Всі лінійні кути двогранного кута рівні один одному.
А
В
O
А1
В1
O
1
Промені ОА та О1А1 – співняпрямлені.
Промені ОВ та О1В1 – співнапрямлені.
Кути АОВ та А1О1В1 рівні,
як кути зі співнапрямленими сторонами.
Двогранні кути можна порівнювати: більший той, у якого більштй лінійний кут.
А
В
O
А1
В1
O
1
Промені ОА та О1А1 – співняпрямлені.
Промені ОВ та О1В1 – співнапрямлені.
Кути АОВ та А1О1В1 рівні,
як кути зі співнапрямленими сторонами.
Двогранні кути можна порівнювати: більший той, у якого більштй лінійний кут.
Слайд #10
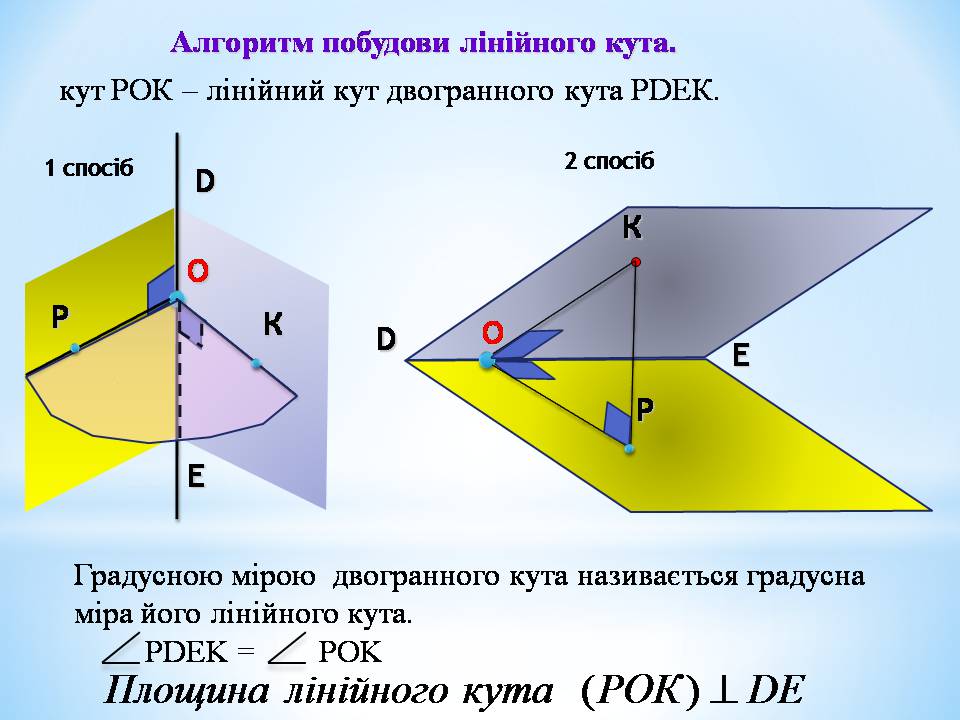
кут РОК – лінійний кут двогранного кута РDEК.
D
E
Градусною мірою двогранного кута називається градусна міра його лінійного кута.
PDEK = POK
Алгоритм побудови лінійного кута.
D
E
O
К
O
Р
К
1 спосіб
2 спосіб
Р
D
E
Градусною мірою двогранного кута називається градусна міра його лінійного кута.
PDEK = POK
Алгоритм побудови лінійного кута.
D
E
O
К
O
Р
К
1 спосіб
2 спосіб
Р
Слайд #11
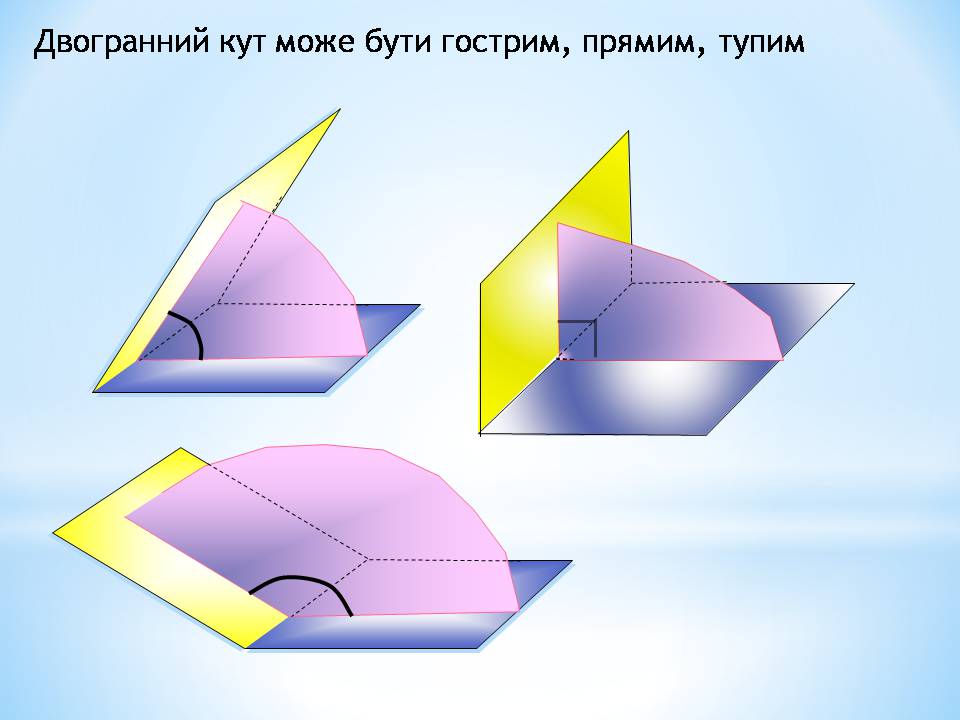
Двогранний кут може бути гострим, прямим, тупим
Слайд #12
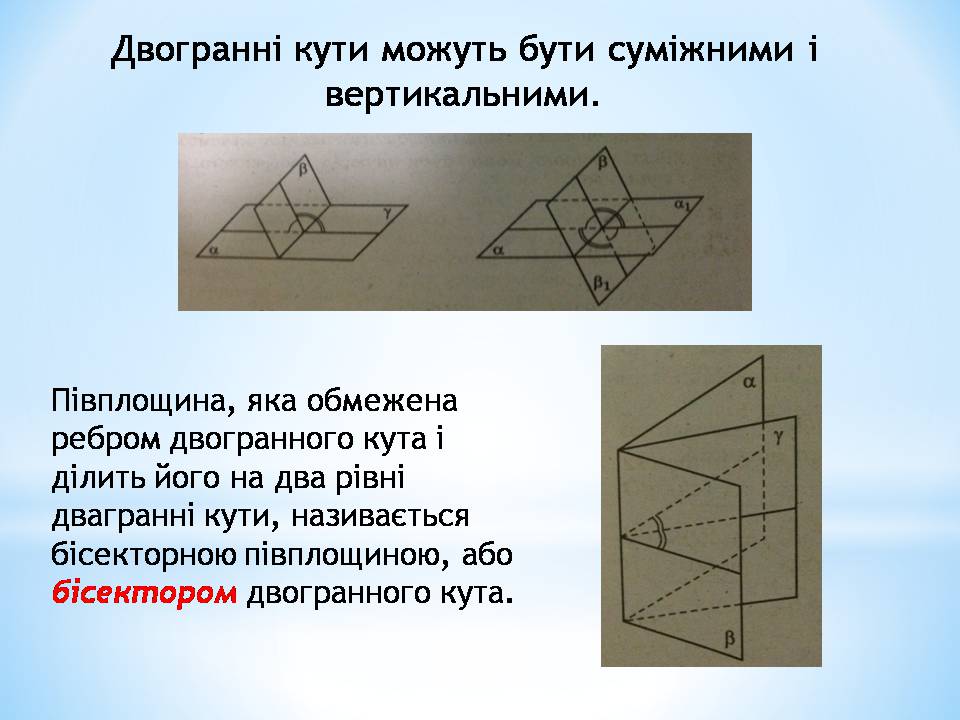
Двогранні кути можуть бути суміжними і вертикальними.
Півплощина, яка обмежена ребром двогранного кута і ділить його на два рівні двагранні кути, називається бісекторною півплощиною, або бісектором двогранного кута.
Півплощина, яка обмежена ребром двогранного кута і ділить його на два рівні двагранні кути, називається бісекторною півплощиною, або бісектором двогранного кута.
Слайд #13
Двогранні кути можуть бути суміжними і вертикальними.
Півплощина, яка обмежена ребром двогранного кута і ділить його на два рівні двагранні кути, називається бісекторною півплощиною, або бісектором двогранного кута.
Півплощина, яка обмежена ребром двогранного кута і ділить його на два рівні двагранні кути, називається бісекторною півплощиною, або бісектором двогранного кута.

Слайд #14
Двогранні кути можуть бути суміжними і вертикальними.
Півплощина, яка обмежена ребром двогранного кута і ділить його на два рівні двагранні кути, називається бісекторною півплощиною, або бісектором двогранного кута.
Півплощина, яка обмежена ребром двогранного кута і ділить його на два рівні двагранні кути, називається бісекторною півплощиною, або бісектором двогранного кута.
Слайд #15
Двогранні кути можуть бути суміжними і вертикальними.
Півплощина, яка обмежена ребром двогранного кута і ділить його на два рівні двагранні кути, називається бісекторною півплощиною, або бісектором двогранного кута.
Півплощина, яка обмежена ребром двогранного кута і ділить його на два рівні двагранні кути, називається бісекторною півплощиною, або бісектором двогранного кута.

Слайд #16
Двогранні кути можуть бути суміжними і вертикальними.
Півплощина, яка обмежена ребром двогранного кута і ділить його на два рівні двагранні кути, називається бісекторною півплощиною, або бісектором двогранного кута.
Півплощина, яка обмежена ребром двогранного кута і ділить його на два рівні двагранні кути, називається бісекторною півплощиною, або бісектором двогранного кута.

Слайд #17
Д.з. вивчити конспект, прочитати параграф15, розібрати вправи на с. 107-108, виконати вправи 521, 526, 532 (б).
Зробити конспект параграфа 17, відповівши на питання на с.120. розібрати вправи на с. 121-122, виконати вправи 591, 592, 593.
Зробити конспект параграфа 17, відповівши на питання на с.120. розібрати вправи на с. 121-122, виконати вправи 591, 592, 593.
