Презентація на тему «Трикутники»
242
Слайд #1
(Типи трикутників, лінії пов'язані з трикутником,основні факти,обчислення площі трикутника)
Трикутники
Трикутники
Слайд #2
Визначення:
Трикутник— це три точки, що не лежать на одній прямій, і три відрізки, що їх сполучають.
Трикутник— це три точки, що не лежать на одній прямій, і три відрізки, що їх сполучають.
Слайд #3
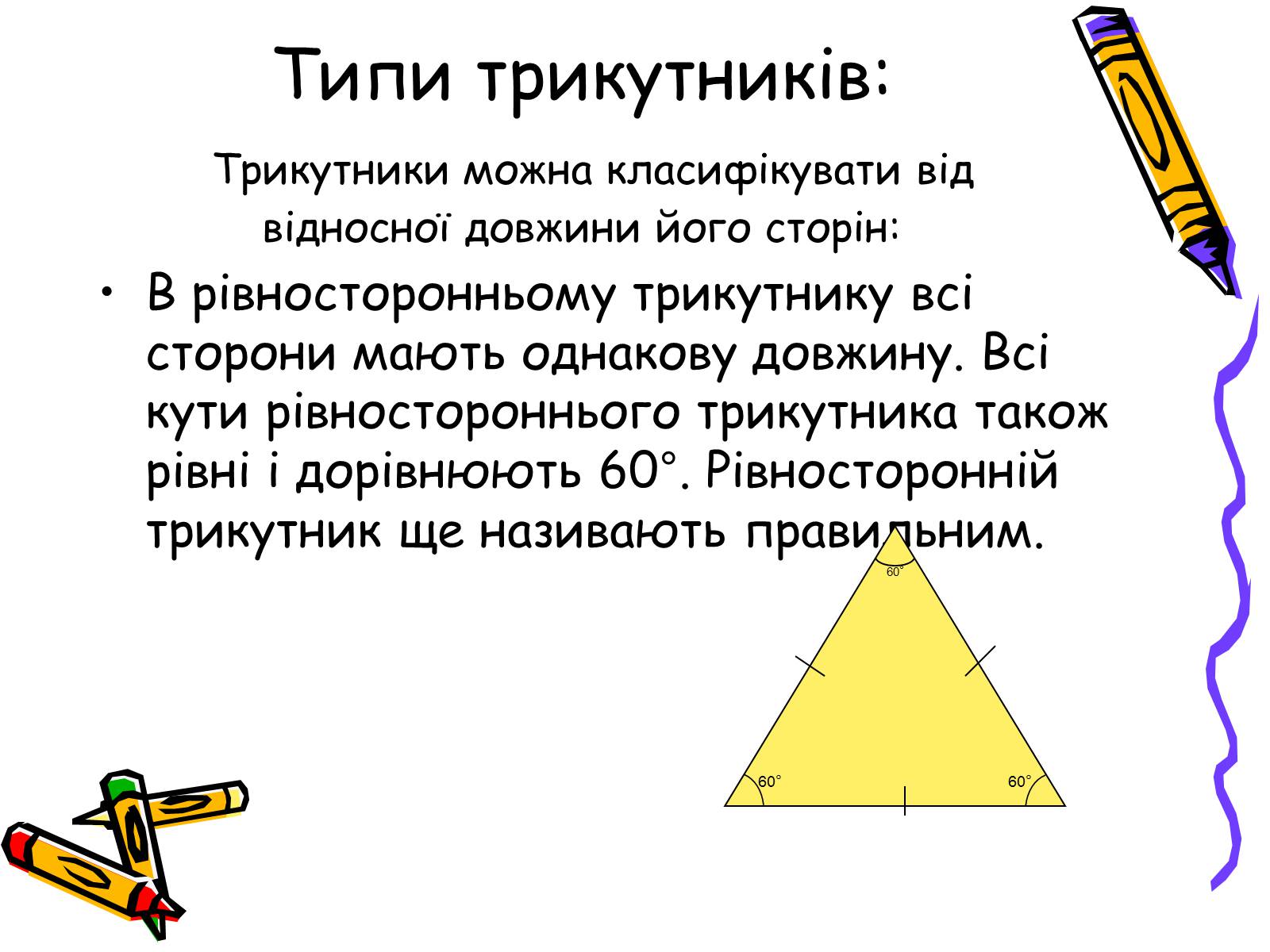
В рівносторонньому трикутнику всі сторони мають однакову довжину. Всі кути рівностороннього трикутника також рівні і дорівнюють 60°. Рівносторонній трикутник ще називають правильним.
Типи трикутників: Трикутники можна класифікувати від відносної довжини його сторін:
60°
60°
60°
Типи трикутників: Трикутники можна класифікувати від відносної довжини його сторін:
60°
60°
60°
Слайд #4
В рівнобедреному трикутнику дві сторони мають однакову довжину, третя сторона при цьому називається основою трикутника. Рівнобедрений трикутник також має однакові кути, які знаходяться при його основі.
Слайд #5
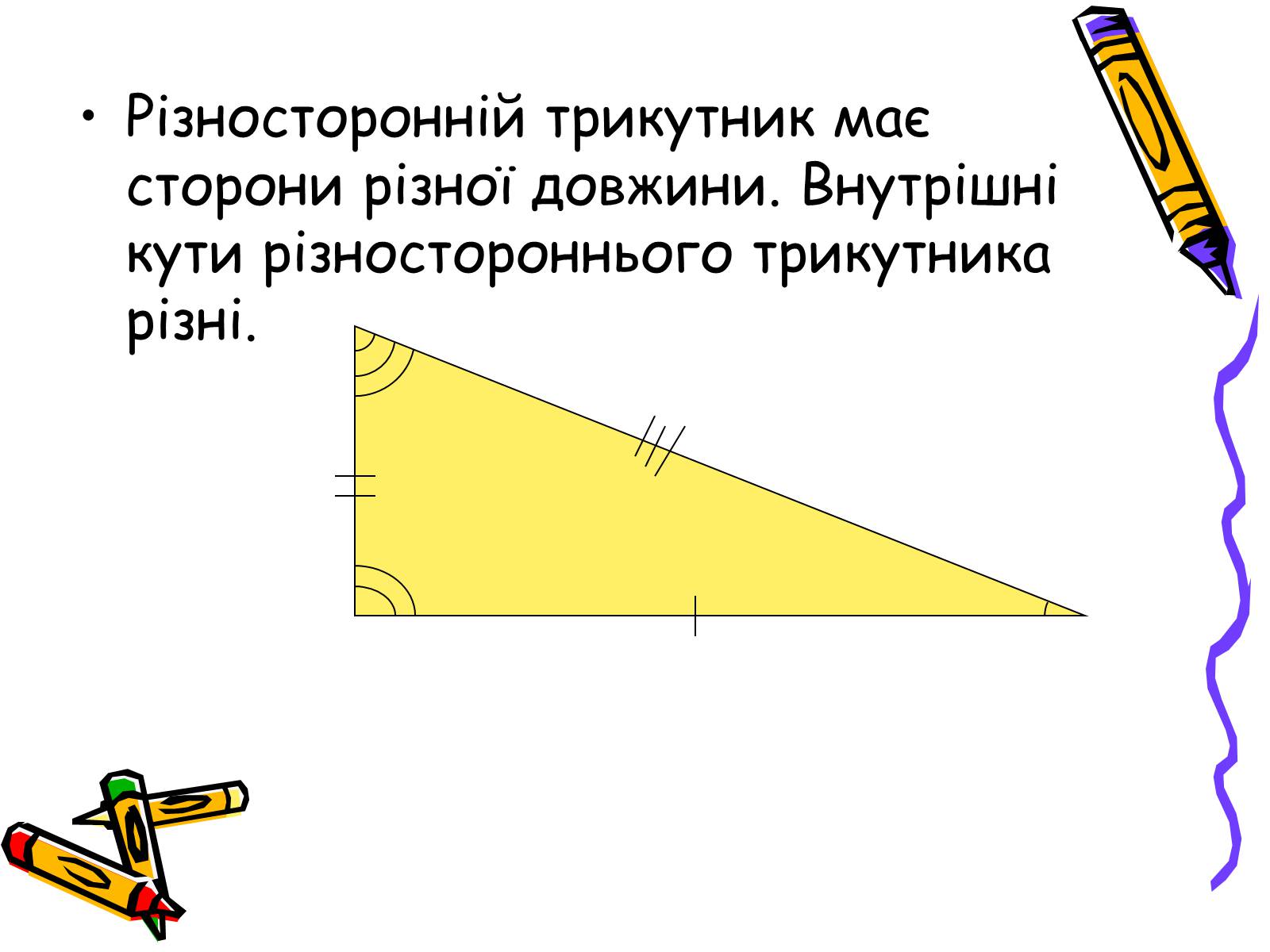
Різносторонній трикутник має сторони різної довжини. Внутрішні кути різностороннього трикутника різні.
Слайд #6
Також трикутники можна класифікувати відповідно до їх внутрішніх кутів:
Прямокутний трикутник має один внутрішній кут рівний 90° (прямий кут). Сторона, протилежна до прямого кута, називається гіпотенуза. Інші дві сторони називаються катетами прямокутного трикутника.
90°
Прямокутний трикутник має один внутрішній кут рівний 90° (прямий кут). Сторона, протилежна до прямого кута, називається гіпотенуза. Інші дві сторони називаються катетами прямокутного трикутника.
90°
Слайд #7
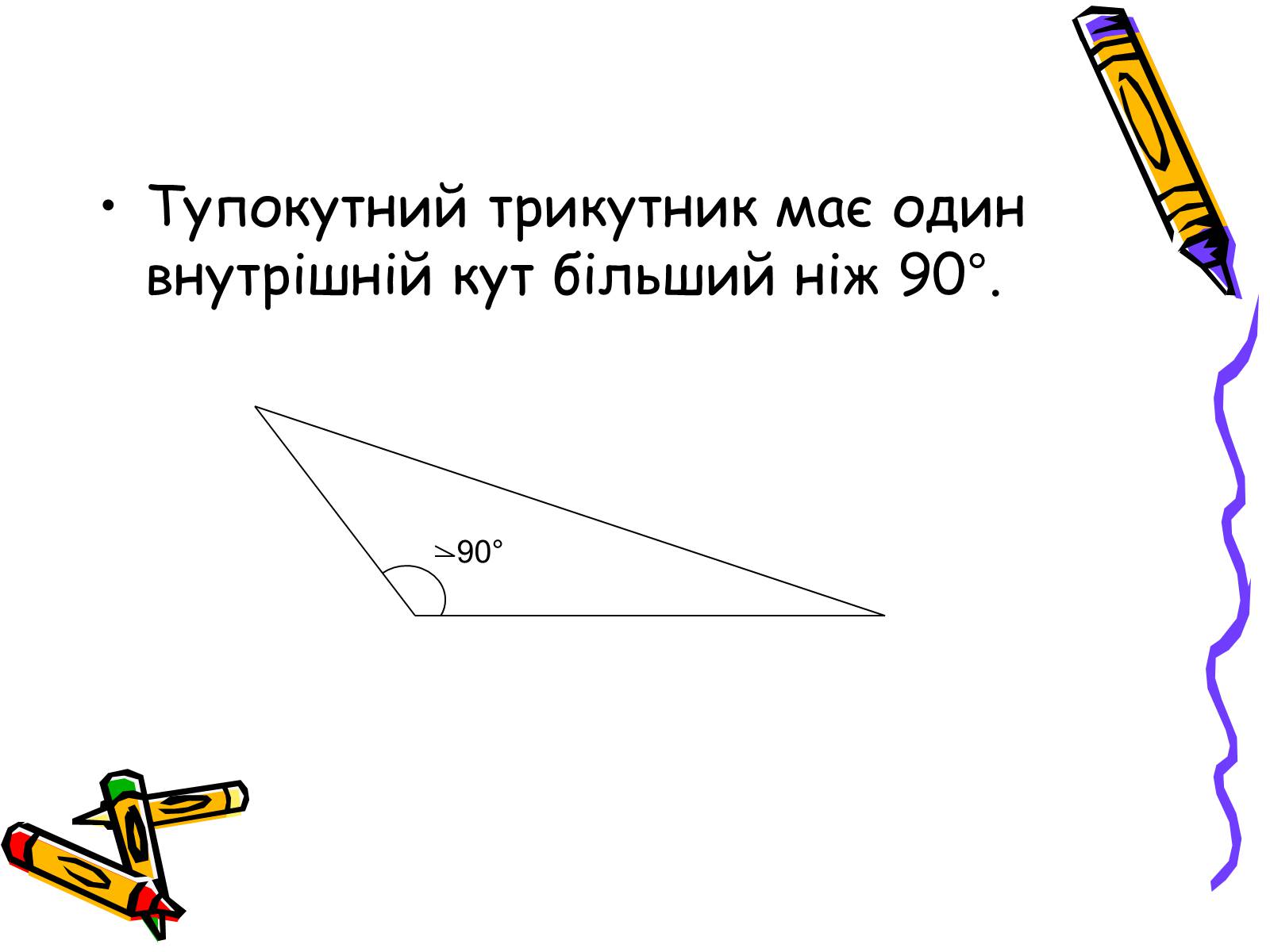
Тупокутний трикутник має один внутрішній кут більший ніж 90°.
90°
90°
Слайд #8
В гострокутному трикутнику всі кути менші за 90°. Рівносторонній трикутник є гострокутним, але не всі гострокутні трикутники рівносторонні.
90
90
90
90
90
90
Слайд #9
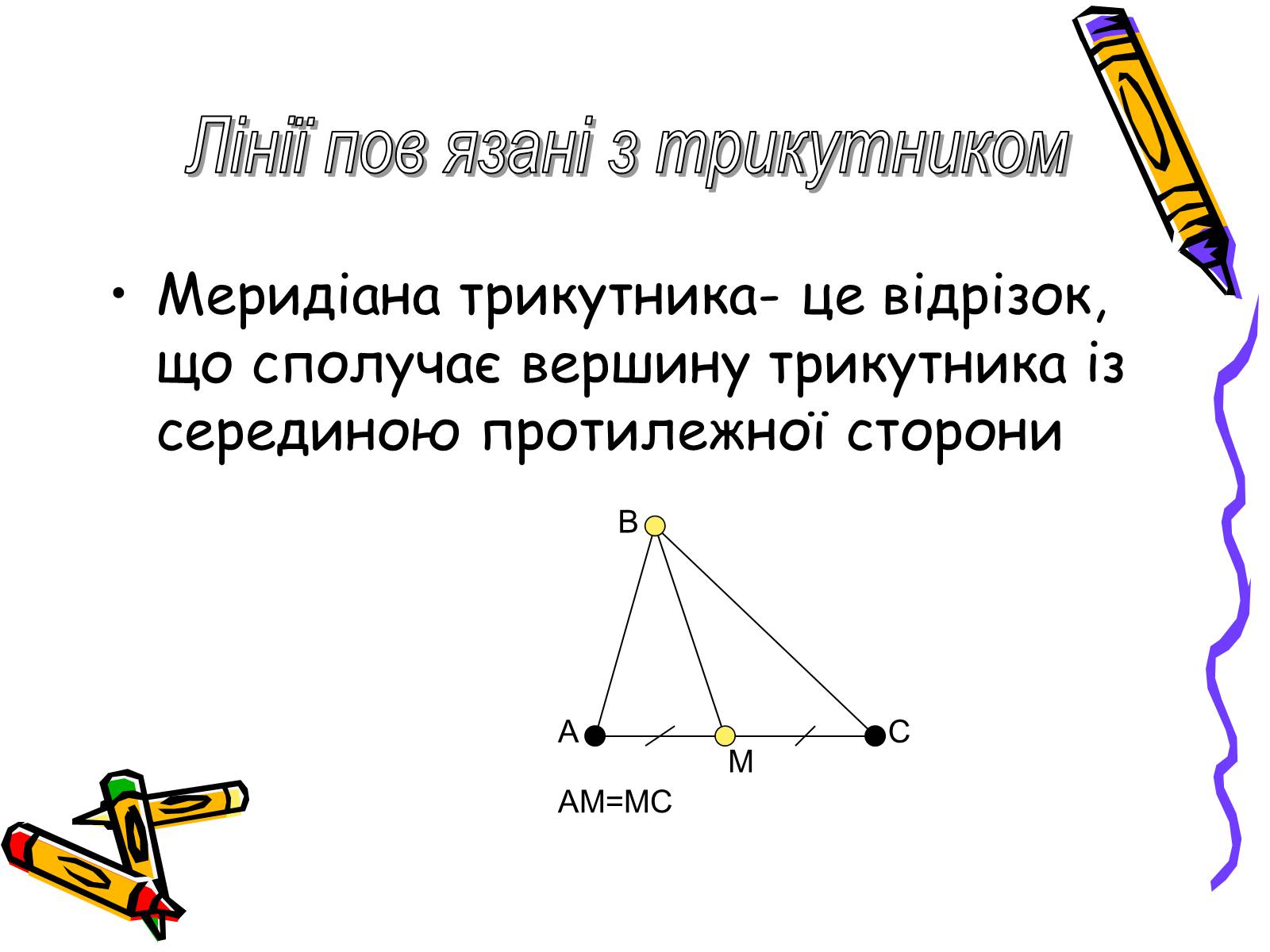
Меридіана трикутника- це відрізок, що сполучає вершину трикутника із серединою протилежної сторони
А
В
М
С
AM=MC
Лінії пов язані з трикутником
А
В
М
С
AM=MC
Лінії пов язані з трикутником
Слайд #10
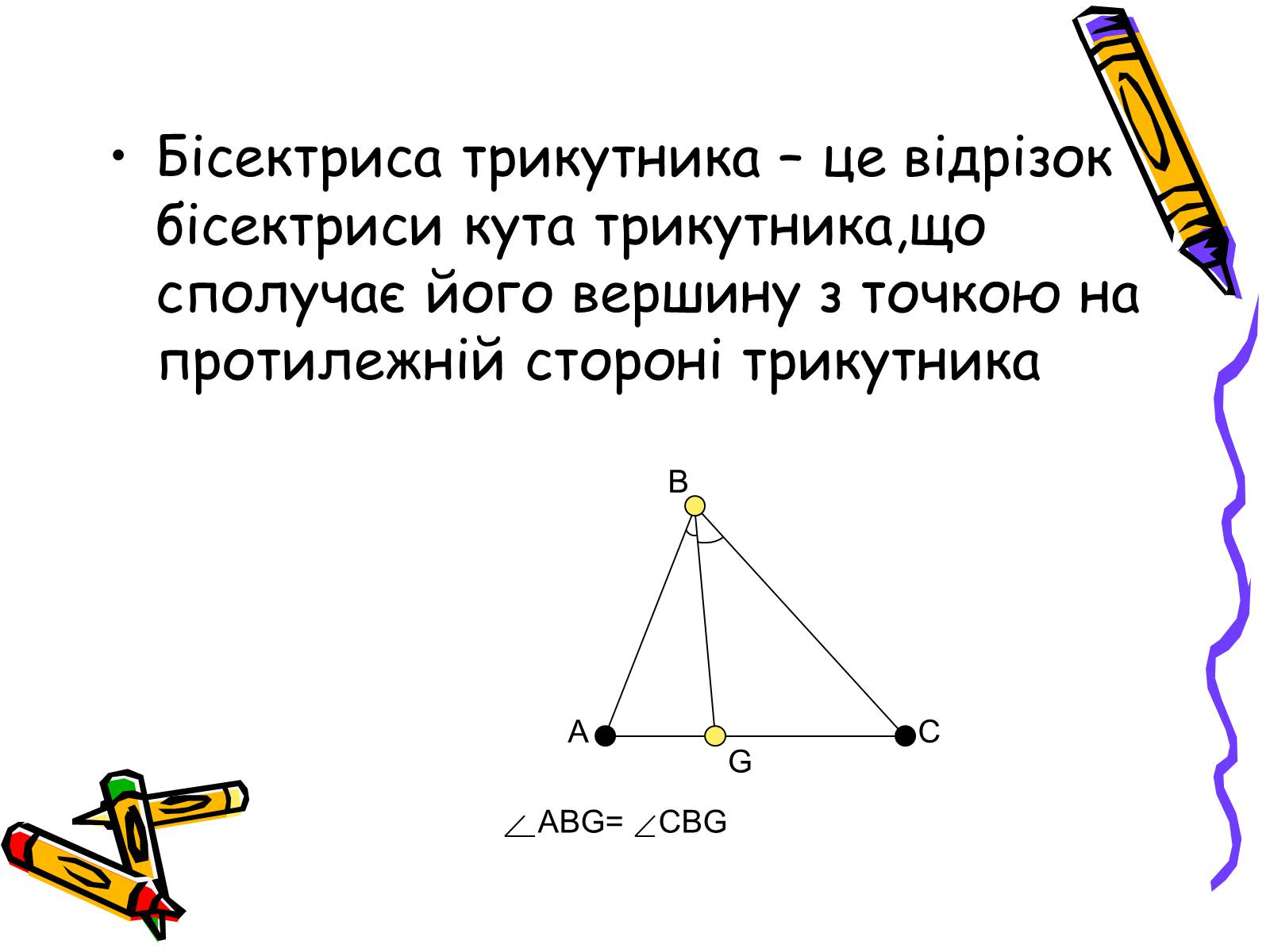
Бісектриса трикутника – це відрізок бісектриси кута трикутника,що сполучає його вершину з точкою на протилежній стороні трикутника
А
В
С
G
ABG= CBG
А
В
С
G
ABG= CBG
Слайд #11
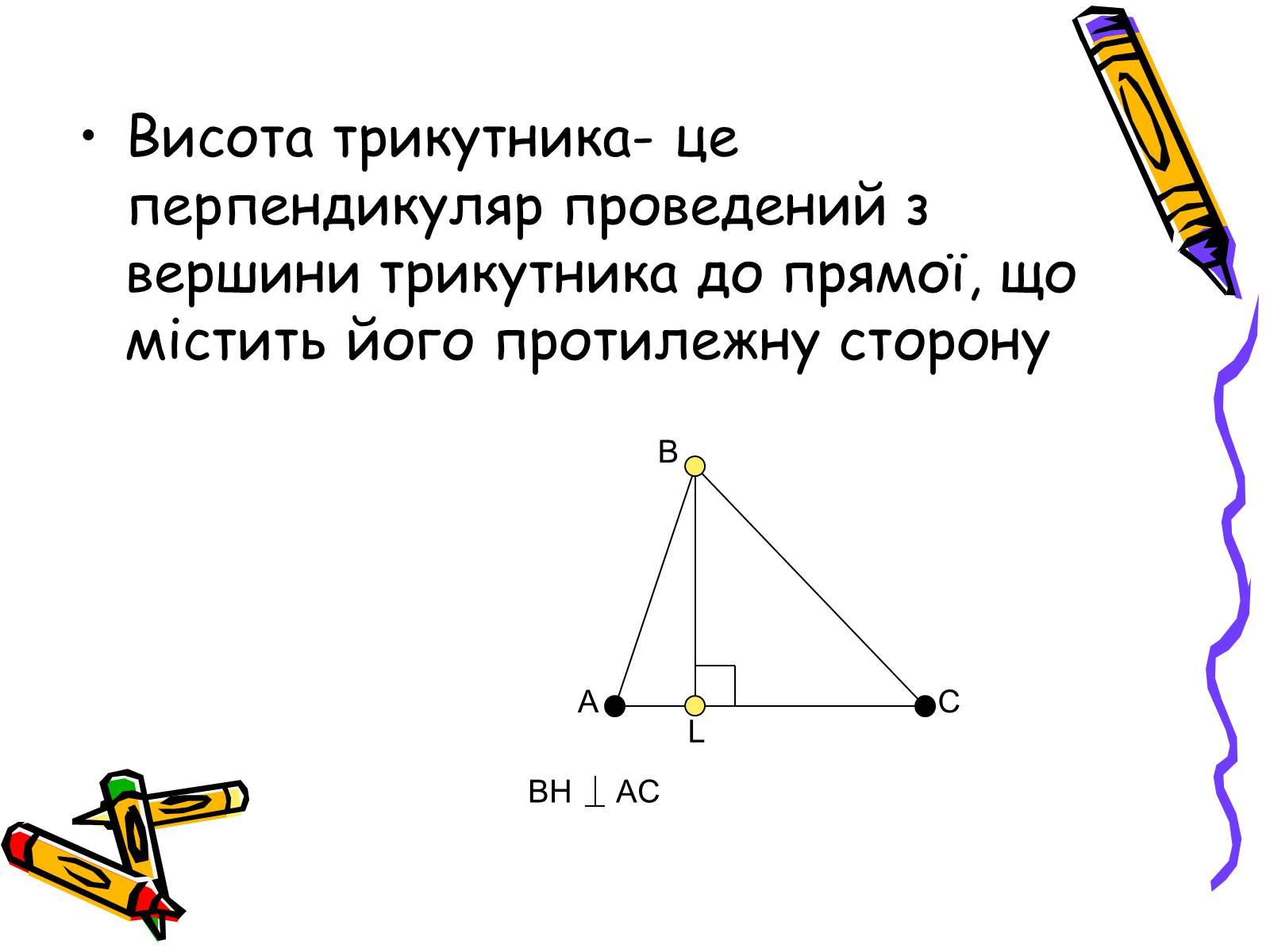
Висота трикутника- це перпендикуляр проведений з вершини трикутника до прямої, що містить його протилежну сторону
А
В
С
L
BH AC
А
В
С
L
BH AC
Слайд #12
Основні Факти
Слайд #13
Вершини трикутника зазвичай позначають великими латинськими літерами A, B, C, кути при відповідних вершинах грецькими літерами α, β, γ, а довжини протилежних сторін — маленькими латинськими літерами a, b, c.
Факт №1
Факт №1
Слайд #14
Сума внутрішніх кутів трикутника — 180 градусів. Сума зовнішніх кутів трикутника 360 градусів.
Факт №2
Факт №2
Слайд #15
Сума довжин двох будь-яких сторін трикутника завжди перевищує довжину третьої сторони. Це є нерівність трикутника або аксіома трикутника
Факт №3
Факт №3
Слайд #16
Обчислення площі трикутника
Слайд #17
Обчислення площі трикутника є простою задачею, яка часто вирішується в багатьох галузях. Найвідоміша і найпростіша формула:
S =
1
2
bh
Де S — площа, b — довжина основи трикутника а h — висота трикутника, відносна до основи. Хоча ця формула й проста, вона може бути використана тільки, якщо можна легко знайти висоту.
S =
1
2
bh
Де S — площа, b — довжина основи трикутника а h — висота трикутника, відносна до основи. Хоча ця формула й проста, вона може бути використана тільки, якщо можна легко знайти висоту.
Слайд #18
Кінець
Дякую,за перегляд*
Дякую,за перегляд*
