- Головна
- Готові шкільні презентації
- Презентація на тему «Взаємне розташування прямих у просторі. Паралельні та мимобіжні прямі»
Презентація на тему «Взаємне розташування прямих у просторі. Паралельні та мимобіжні прямі»
259
Слайд #1
Взаємне розташування прямих у просторі.Паралельні та мимобіжні прямі.
Підготувала: Івєніна Юлія
Підготувала: Івєніна Юлія

Слайд #2
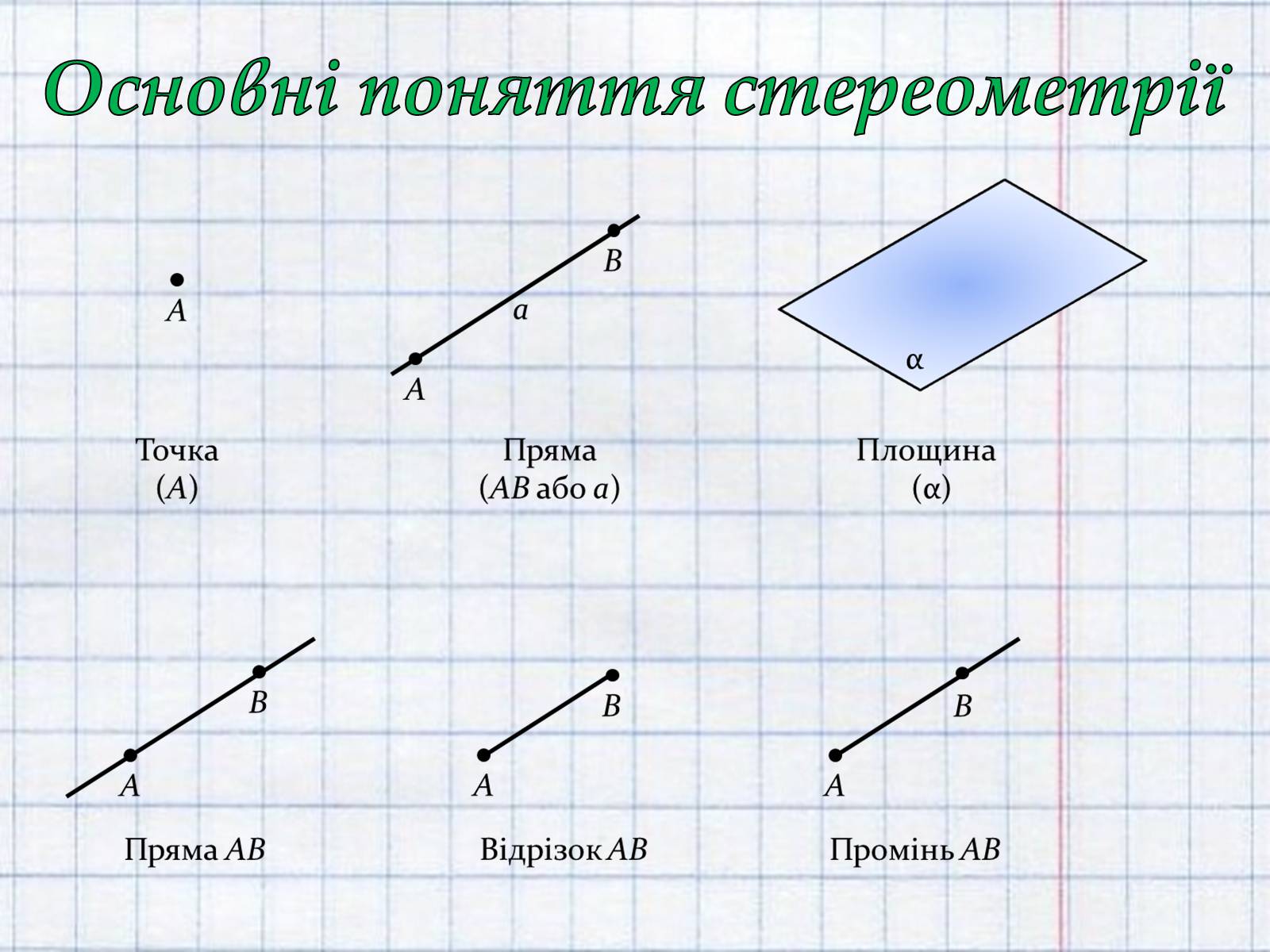
Основні поняття стереометрії
Слайд #3
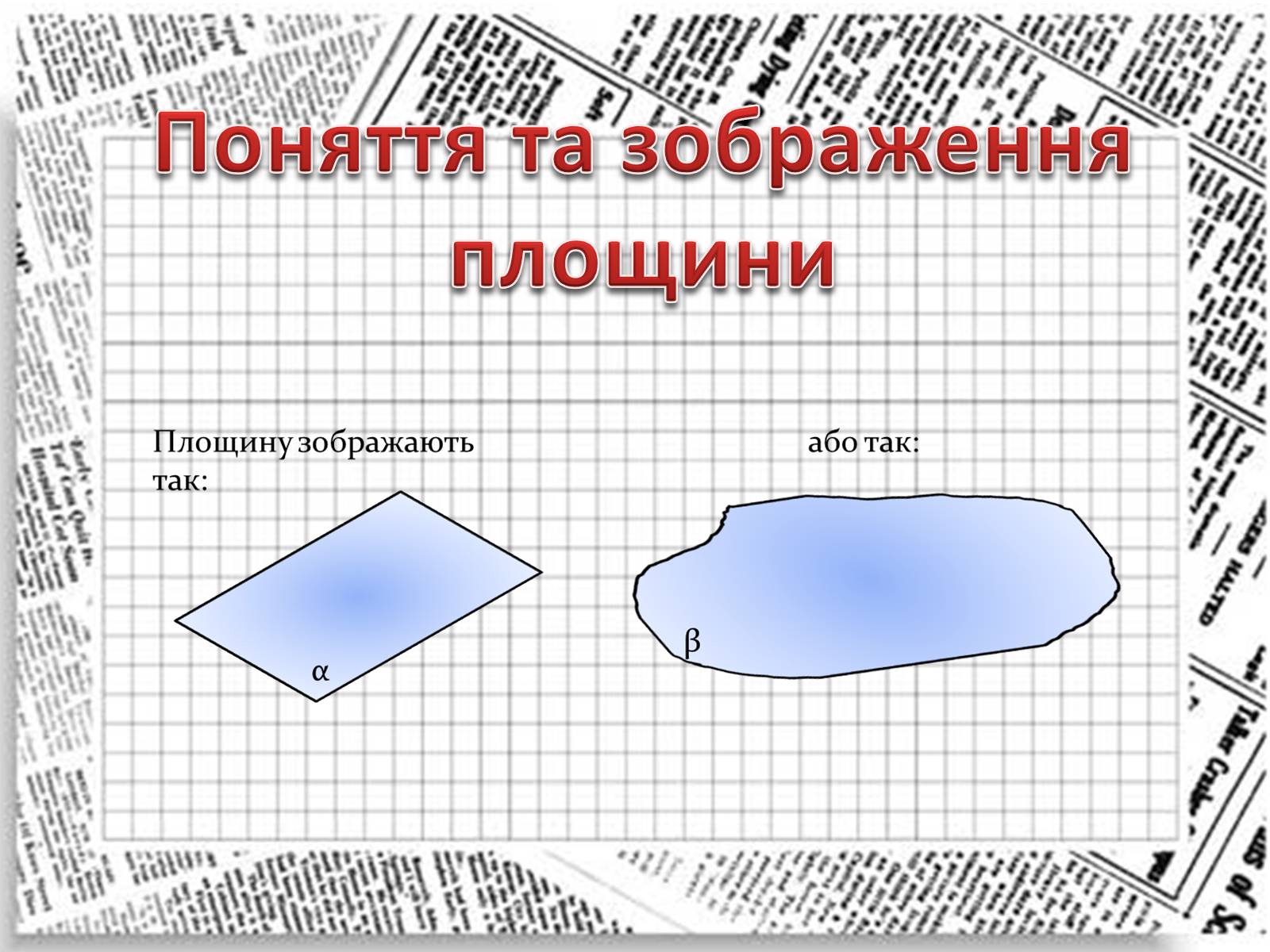
Поняття та зображення
площини
площини
Слайд #4
Зверніть увагу!!!
Площина, так само як і пряма, є нескінченною:
A
Площина, так само як і пряма, є нескінченною:
A

Слайд #5
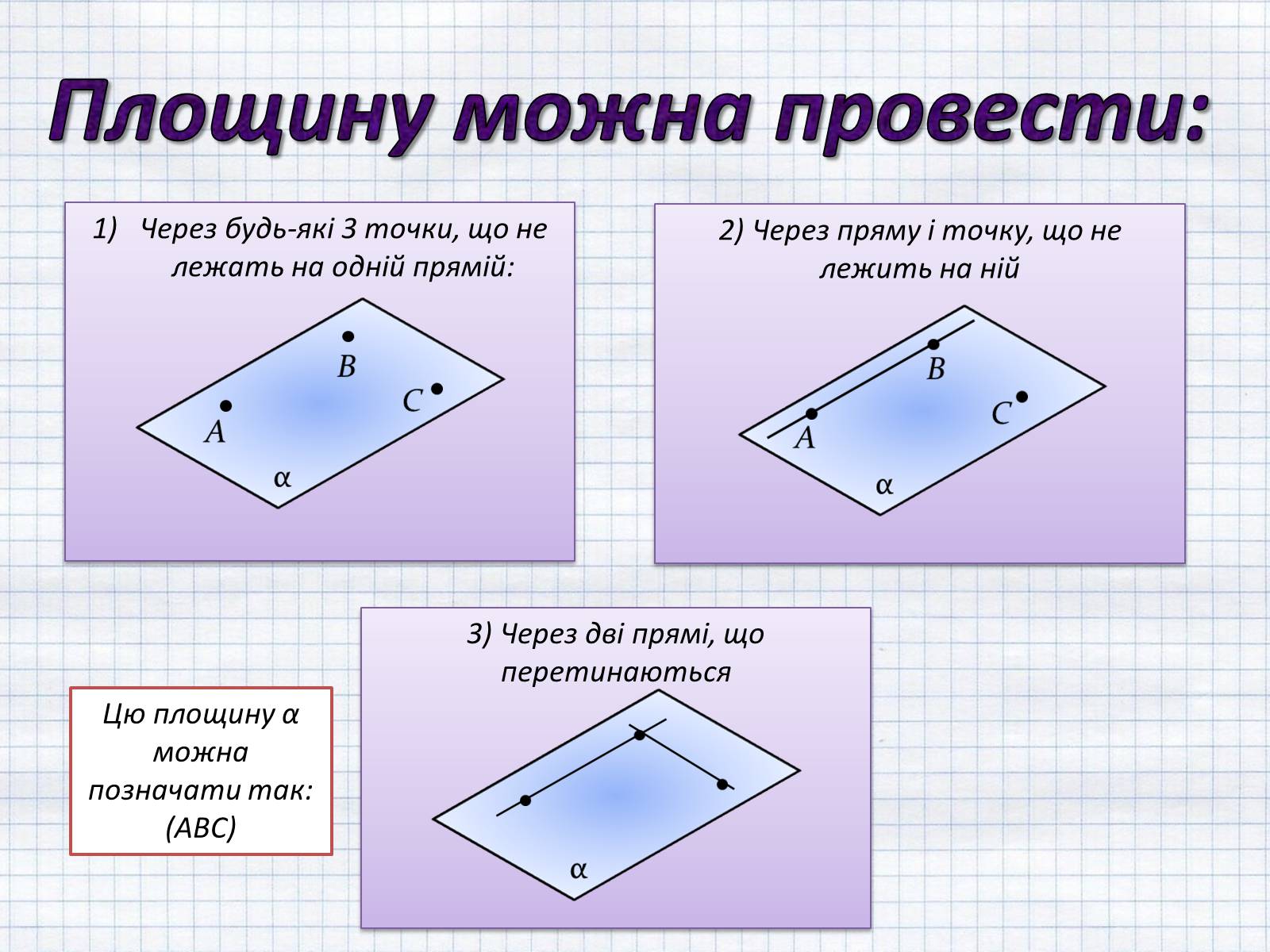
Площину можна провести:
Через будь-які 3 точки, що не лежать на одній прямій:
2) Через пряму і точку, що не лежить на ній
3) Через дві прямі, що перетинаються
Цю площину α можна позначати так: (АВС)
Через будь-які 3 точки, що не лежать на одній прямій:
2) Через пряму і точку, що не лежить на ній
3) Через дві прямі, що перетинаються
Цю площину α можна позначати так: (АВС)
Слайд #6
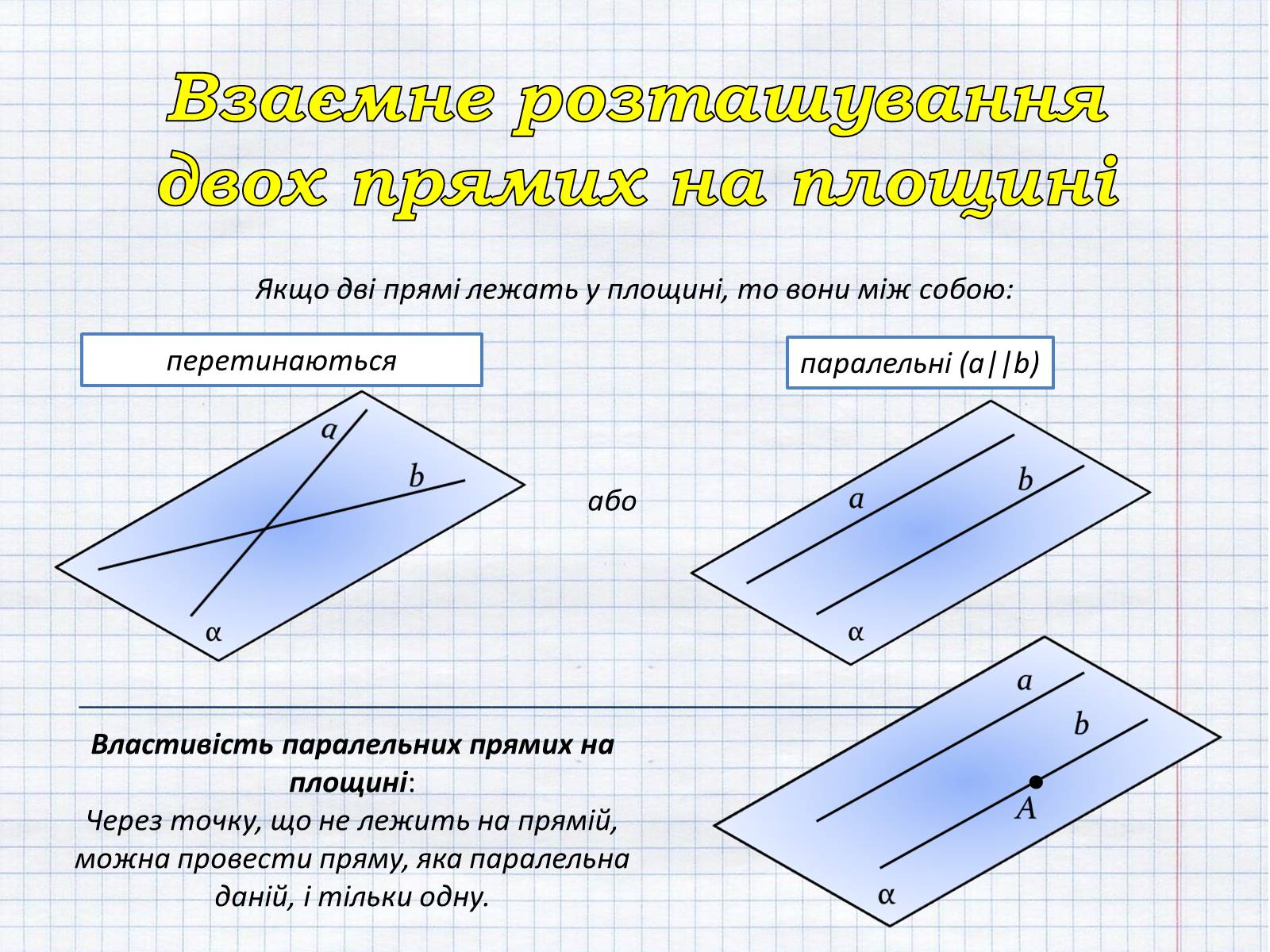
Взаємне розташування двох прямих на площині
Якщо дві прямі лежать у площині, то вони між собою:
перетинаються
або
паралельні (a||b)
___________________________________________________________________
Властивість паралельних прямих на площині:
Через точку, що не лежить на прямій, можна провести пряму, яка паралельна даній, і тільки одну.
●
Якщо дві прямі лежать у площині, то вони між собою:
перетинаються
або
паралельні (a||b)
___________________________________________________________________
Властивість паралельних прямих на площині:
Через точку, що не лежить на прямій, можна провести пряму, яка паралельна даній, і тільки одну.
●
Слайд #7
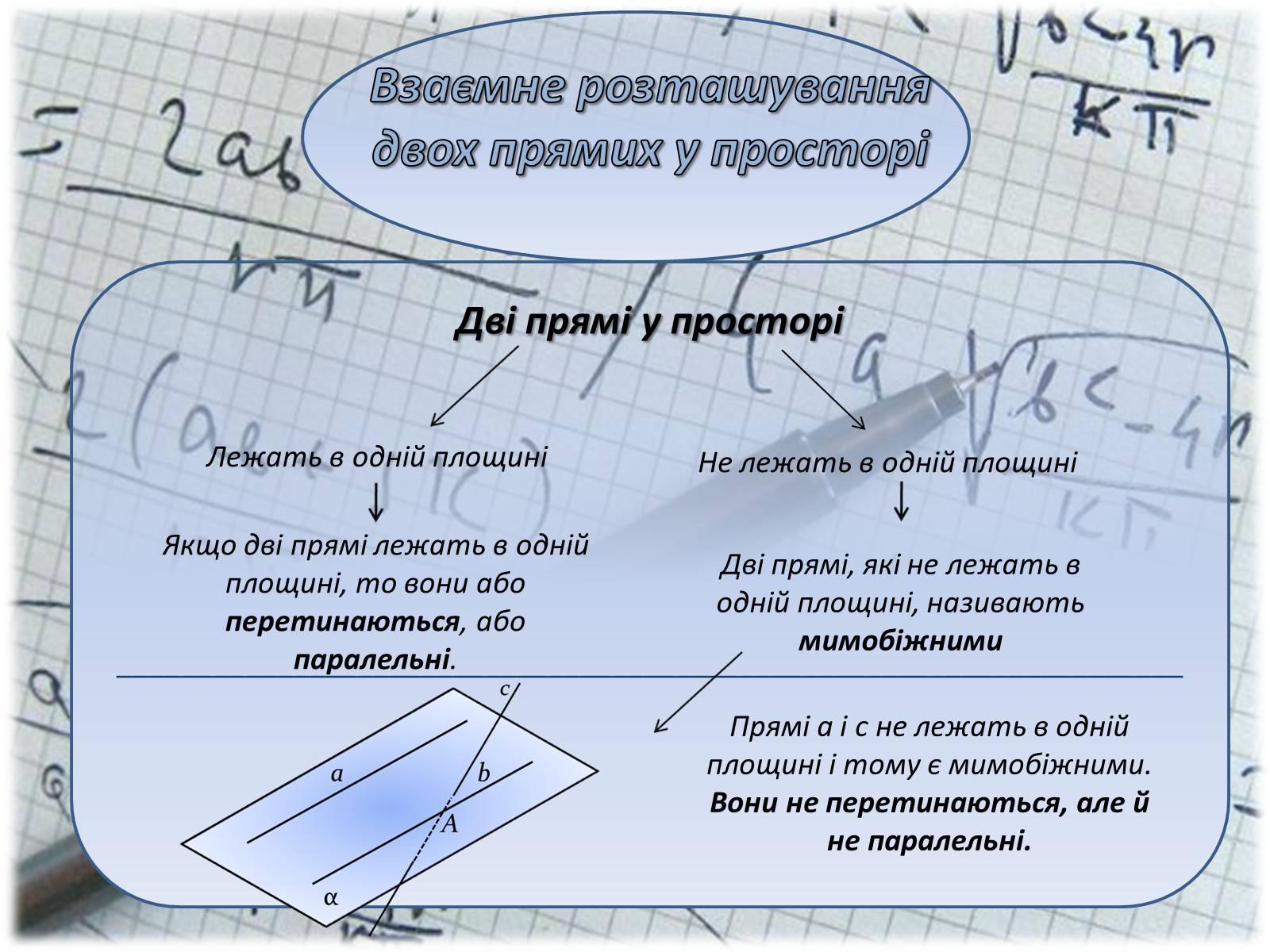
Взаємне розташування двох прямих у просторі
Дві прямі у просторі
Лежать в одній площині
Не лежать в одній площині
Якщо дві прямі лежать в одній площині, то вони або перетинаються, або паралельні.
Дві прямі, які не лежать в одній площині, називають мимобіжними
Прямі a і c не лежать в одній площині і тому є мимобіжними.
Вони не перетинаються, але й не паралельні.
Дві прямі у просторі
Лежать в одній площині
Не лежать в одній площині
Якщо дві прямі лежать в одній площині, то вони або перетинаються, або паралельні.
Дві прямі, які не лежать в одній площині, називають мимобіжними
Прямі a і c не лежать в одній площині і тому є мимобіжними.
Вони не перетинаються, але й не паралельні.
Слайд #8
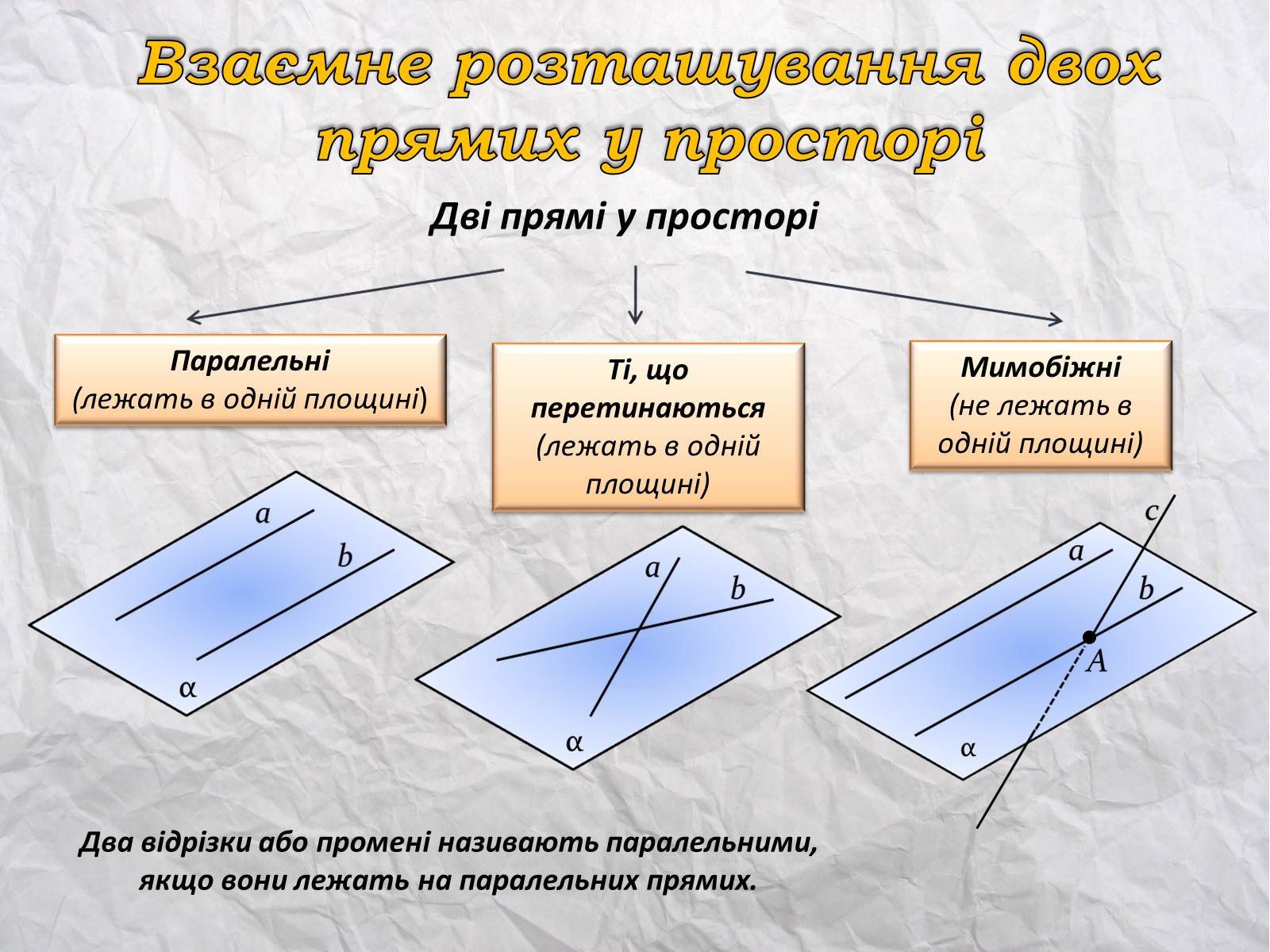
Взаємне розташування двох прямих у просторі
Дві прямі у просторі
Паралельні
(лежать в одній площині)
Ті, що перетинаються(лежать в одній площині)
Мимобіжні(не лежать в одній площині)
●
Два відрізки або промені називають паралельними, якщо вони лежать на паралельних прямих.
Дві прямі у просторі
Паралельні
(лежать в одній площині)
Ті, що перетинаються(лежать в одній площині)
Мимобіжні(не лежать в одній площині)
●
Два відрізки або промені називають паралельними, якщо вони лежать на паралельних прямих.
Слайд #9
Теореми про паралельні прямі
Через будь-яку точку простору, яка не лежить на даній прямій, можна провести пряму, паралельну даній, і тільки одну.
!
Дано:
пряма а, точка А є а.
Довести:
1) через а можна провести b||a;
2) ця пряма b буде єдиною.Доведення:
1) Через пряму а і точку А можна провести єдину площину(теорема 1).2) У цій площині можна провести пряму, паралельну даній, і тільки одну (проводимо пряму b).Отже, у просторі можна провести одну пряму, паралельну даній.
Дві прямі, паралельні третій, паралельні.
Властивість паралельних прямих на площині (аксіома з 7 класу):
Через точку, що не лежить на прямій, можна провести пряму, яка паралельна даній, і тільки одну.
Через будь-яку точку простору, яка не лежить на даній прямій, можна провести пряму, паралельну даній, і тільки одну.
!
Дано:
пряма а, точка А є а.
Довести:
1) через а можна провести b||a;
2) ця пряма b буде єдиною.Доведення:
1) Через пряму а і точку А можна провести єдину площину(теорема 1).2) У цій площині можна провести пряму, паралельну даній, і тільки одну (проводимо пряму b).Отже, у просторі можна провести одну пряму, паралельну даній.
Дві прямі, паралельні третій, паралельні.
Властивість паралельних прямих на площині (аксіома з 7 класу):
Через точку, що не лежить на прямій, можна провести пряму, яка паралельна даній, і тільки одну.

Слайд #10
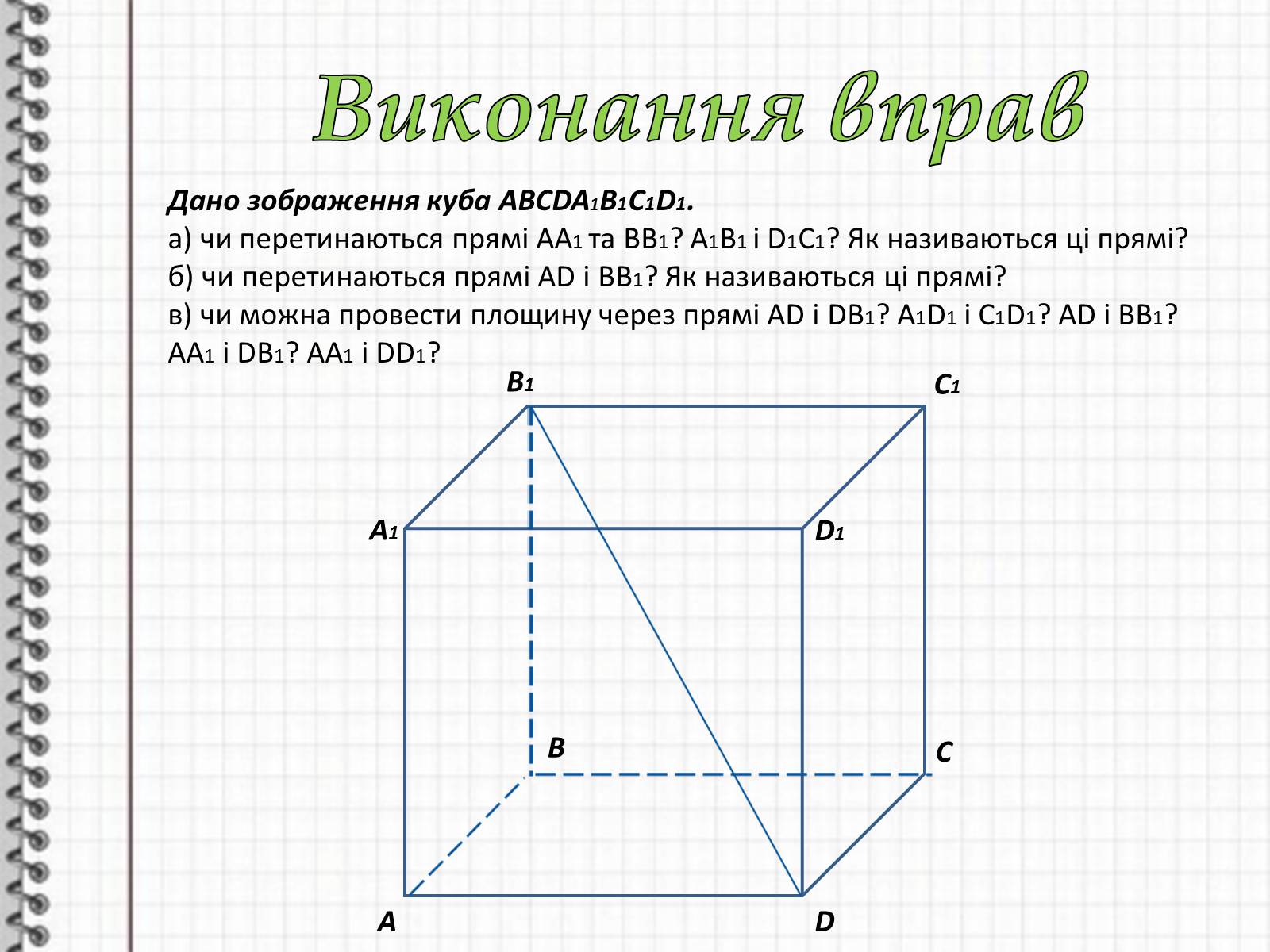
Виконання вправ
Дано зображення куба ABCDA1B1C1D1.
а) чи перетинаються прямі АА1 та ВВ1? А1В1 і D1C1? Як називаються ці прямі?
б) чи перетинаються прямі AD і BB1? Як називаються ці прямі?
в) чи можна провести площину через прямі AD і DB1? A1D1 i C1D1? AD i BB1? AA1 i DB1? AA1 i DD1?
А
D
В
С
А1
В1
С1
D1
Дано зображення куба ABCDA1B1C1D1.
а) чи перетинаються прямі АА1 та ВВ1? А1В1 і D1C1? Як називаються ці прямі?
б) чи перетинаються прямі AD і BB1? Як називаються ці прямі?
в) чи можна провести площину через прямі AD і DB1? A1D1 i C1D1? AD i BB1? AA1 i DB1? AA1 i DD1?
А
D
В
С
А1
В1
С1
D1
Слайд #11
Виконання вправ
Задача
Прямі AB і CD паралельні. Чи можуть бути мимобіжними прямі AC і BD? А чи можуть вони перетинатись?
Розв'язання
Якщо AB||CD, то прямі AB і CD лежать в одній площині, значить, і точки A, B, C, D лежать в одній площині. Отже, прямі AC і BD також лежать в одній площині, а значить, можуть перетинатися, але не можуть бути мимобіжними.
Задача
Прямі AB і CD паралельні. Чи можуть бути мимобіжними прямі AC і BD? А чи можуть вони перетинатись?
Розв'язання
Якщо AB||CD, то прямі AB і CD лежать в одній площині, значить, і точки A, B, C, D лежать в одній площині. Отже, прямі AC і BD також лежать в одній площині, а значить, можуть перетинатися, але не можуть бути мимобіжними.

Слайд #12
Виконання вправ
Задача
Прямі AB і CD мимобіжні. Чи можуть бути паралельними прямі AC і BD? А чи можуть вони перетинатись?
Розв'язання
Якщо б могло бути, що AC||BD або AC перетинала BD,то точки A, B, C, D лежали б в одній площині,а цього бути не може, тому що суперечить умові задачі.
Отже, прямі AC і BD не можуть бути ні паралельними, ні перетинатись.
Задача
Прямі AB і CD мимобіжні. Чи можуть бути паралельними прямі AC і BD? А чи можуть вони перетинатись?
Розв'язання
Якщо б могло бути, що AC||BD або AC перетинала BD,то точки A, B, C, D лежали б в одній площині,а цього бути не може, тому що суперечить умові задачі.
Отже, прямі AC і BD не можуть бути ні паралельними, ні перетинатись.

Слайд #13
Дякую за увагу!
