- Головна
- Готові шкільні презентації
- Презентація на тему «Формули скороченого множення» (варіант 4)
Презентація на тему «Формули скороченого множення» (варіант 4)
2308
Слайд #1
Формули скороченого множення
Підготувала
Каменська Світлана Іванівна
ЗОШ № 20 м. Дзержинськ
Донецька область
Підготувала
Каменська Світлана Іванівна
ЗОШ № 20 м. Дзержинськ
Донецька область

Слайд #2
Тема: Формули скороченого множення
Мета вивчення теми:
вивчити формули скороченого множення: квадрат двочлена, різниця квадратів,
сума і різниця кубів, куб суми і різниці двох виразів;
домогтися свідомого розуміння учнями змісту формул скороченого множення;
виробити вміння записувати, читати та застосовувати формули для розв'язування
вправ;
формувати вміння та навички застосовування цих формул для спрощення виразів,
розв'язування рівнянь, доведення тотожностей, доведення подільності;
формувати вміння ти навички виконувати розкладання многочленів на множники
за формулами скороченого множення та із застосуванням декількох способів.
Знати:
формули скороченого множення: квадрат двочлена, різниця квадратів, сума і
різниця кубів, куб суми і різниці двох виразів.
Вміти:
застосовувати формули скороченого множення для спрощення виразів,
розв'язування рівнянь, доведення тотожностей, доведення подільності;
розкладати многочлени на множники за формулами скороченого множення та із
застосуванням декількох способів.
Мета вивчення теми:
вивчити формули скороченого множення: квадрат двочлена, різниця квадратів,
сума і різниця кубів, куб суми і різниці двох виразів;
домогтися свідомого розуміння учнями змісту формул скороченого множення;
виробити вміння записувати, читати та застосовувати формули для розв'язування
вправ;
формувати вміння та навички застосовування цих формул для спрощення виразів,
розв'язування рівнянь, доведення тотожностей, доведення подільності;
формувати вміння ти навички виконувати розкладання многочленів на множники
за формулами скороченого множення та із застосуванням декількох способів.
Знати:
формули скороченого множення: квадрат двочлена, різниця квадратів, сума і
різниця кубів, куб суми і різниці двох виразів.
Вміти:
застосовувати формули скороченого множення для спрощення виразів,
розв'язування рівнянь, доведення тотожностей, доведення подільності;
розкладати многочлени на множники за формулами скороченого множення та із
застосуванням декількох способів.

Слайд #3
Урок 1
У математиків
існує своя мова –
це формули.
С.В. Ковалевська.
У математиків
існує своя мова –
це формули.
С.В. Ковалевська.

Слайд #4
Множення різниці двох виразів на їх суму
( a – b )( a + b ) = a² – b²
Добуток різниці двох виразів та їх суми дорівнює різниці квадратів цих виразів.
Приклади: a) (k – n)(k + n) = k² – n²;
b) (2х – 3у)(2х + 3у)=4x² – 9y².
( a – b )( a + b ) = a² – b²
Добуток різниці двох виразів та їх суми дорівнює різниці квадратів цих виразів.
Приклади: a) (k – n)(k + n) = k² – n²;
b) (2х – 3у)(2х + 3у)=4x² – 9y².

Слайд #5
Усні завдання
Вписати пропущені вирази, щоб отримати правильну рівність:
(4a + 1)(4a – 1) = 16a² – ◊;
(2a – c)(2a + c) = ◊ – c²;
(◊ + x)(◊ – x) = 4d² – ◊;
(a – c²)(a + c²) = ◊ – c4;
2(4x – 1)(4x + 1) = 2(16x² – ◊) = 32x² – ◊;
(a – 2b)(a + 2b) + 4b² = ◊ – 4b² + ◊ = a².
Вписати пропущені вирази, щоб отримати правильну рівність:
(4a + 1)(4a – 1) = 16a² – ◊;
(2a – c)(2a + c) = ◊ – c²;
(◊ + x)(◊ – x) = 4d² – ◊;
(a – c²)(a + c²) = ◊ – c4;
2(4x – 1)(4x + 1) = 2(16x² – ◊) = 32x² – ◊;
(a – 2b)(a + 2b) + 4b² = ◊ – 4b² + ◊ = a².

Слайд #6
Розкладання на множники різниці квадратів двох виразів
a² – b² = ( a – b )( a + b )
Різниця квадратів двох виразів дорівнює добутку різниці цих виразів та їх суми.
Приклади: 1) 25x² – 9y² = (5х – 3у)(5х + 3у);
2) (х – 2)² - 36=(х – 2 – 6)(х – 2 + 6)=
= (х – 8)(х +4).
Урок 2
a² – b² = ( a – b )( a + b )
Різниця квадратів двох виразів дорівнює добутку різниці цих виразів та їх суми.
Приклади: 1) 25x² – 9y² = (5х – 3у)(5х + 3у);
2) (х – 2)² - 36=(х – 2 – 6)(х – 2 + 6)=
= (х – 8)(х +4).
Урок 2

Слайд #7
Усні завдання
Вписати пропущені вирази, щоб отримати правильну рівність:
x² – m² = (x – m)(x + □);
a² – 9 = (a – 3)(□ + 3);
b² – g4 = (□ – g²)(b + □);
1 -16z² = (1 – □)(1 + 4z);
0,04 – x10 = (0,2 – x5)(□ + x 5);
– c4 + 9a2 = 9a2 – □ = (3a – □)(3a + c2).
Вписати пропущені вирази, щоб отримати правильну рівність:
x² – m² = (x – m)(x + □);
a² – 9 = (a – 3)(□ + 3);
b² – g4 = (□ – g²)(b + □);
1 -16z² = (1 – □)(1 + 4z);
0,04 – x10 = (0,2 – x5)(□ + x 5);
– c4 + 9a2 = 9a2 – □ = (3a – □)(3a + c2).

Слайд #8
Квадрат суми двох виразів
( a + b )² = a² + 2ab + b²
Квадрат суми двох виразів дорівнює квадрату першого виразу плюс подвоєний добуток цих виразів плюс квадрат другого виразу.
Приклади: a) (3 + a)² = 9 + 6a + a²;
b) (5x + 3y)² = 25x² + 30xy + 9y².
Урок 3 – 4
( a + b )² = a² + 2ab + b²
Квадрат суми двох виразів дорівнює квадрату першого виразу плюс подвоєний добуток цих виразів плюс квадрат другого виразу.
Приклади: a) (3 + a)² = 9 + 6a + a²;
b) (5x + 3y)² = 25x² + 30xy + 9y².
Урок 3 – 4

Слайд #9
Квадрат різниці двох виразів
( a – b )² = a² – 2ab + b²
Квадрат різниці двох виразів дорівнює квадрату першого виразу мінус подвоєний добуток цих виразів плюс квадрат другого виразу.
Приклади: a) (3 – a)² = 9 – 6a + a²;
b) (5x – 3y)² = 25x² – 30xy + 9y².
( a – b )² = a² – 2ab + b²
Квадрат різниці двох виразів дорівнює квадрату першого виразу мінус подвоєний добуток цих виразів плюс квадрат другого виразу.
Приклади: a) (3 – a)² = 9 – 6a + a²;
b) (5x – 3y)² = 25x² – 30xy + 9y².

Слайд #10
Завдання для самоконтролю
Вибрати, в якому із стовбців (А, Б, В) записано правильну
відповідь до завдань 1 – 4.
№ з/п
Завдання
Відповіді
А
Б
В
1.
(c + 11)²
c² + 11c + 121
c² - 22c + 121
c² + 22c + 121
2.
(7y + 6)²
49y² + 42y + 36
49y² + 84y + 36
49y² - 84y + 36
3.
(9 – 8y)²
81 – 144y +64y²
81 – 72y +64y²
81 + 144y +64y²
4.
(2x – 3y)²
4x² – 12xy +9y²
4x² + 12xy +9y²
4x² – 6xy +9y²
Вибрати, в якому із стовбців (А, Б, В) записано правильну
відповідь до завдань 1 – 4.
№ з/п
Завдання
Відповіді
А
Б
В
1.
(c + 11)²
c² + 11c + 121
c² - 22c + 121
c² + 22c + 121
2.
(7y + 6)²
49y² + 42y + 36
49y² + 84y + 36
49y² - 84y + 36
3.
(9 – 8y)²
81 – 144y +64y²
81 – 72y +64y²
81 + 144y +64y²
4.
(2x – 3y)²
4x² – 12xy +9y²
4x² + 12xy +9y²
4x² – 6xy +9y²

Слайд #11
Завдання “ Знайди пару ”
Потрібно у правій колонці знайти відповідь до
приклада у лівій колонці.
Приклади Відповіді
А) (0,2a - p³)²; 1. a4 – 16a²p5 + 64p10;
Б) (a² - 8p5)²; 2. 0,25 + 2a² + 2a4;
В) (-a – p²)²; 3. 0,04a² - 0,2ap² + 0,25p4;
Г) (-0,5 – 2a²)²; 4. a² + 2ap² + p4;
Д) (-0,2a + 0,5p²)²; 5. 0,04a² - 0,4ap3 + p6 .
Потрібно у правій колонці знайти відповідь до
приклада у лівій колонці.
Приклади Відповіді
А) (0,2a - p³)²; 1. a4 – 16a²p5 + 64p10;
Б) (a² - 8p5)²; 2. 0,25 + 2a² + 2a4;
В) (-a – p²)²; 3. 0,04a² - 0,2ap² + 0,25p4;
Г) (-0,5 – 2a²)²; 4. a² + 2ap² + p4;
Д) (-0,2a + 0,5p²)²; 5. 0,04a² - 0,4ap3 + p6 .

Слайд #12
Математичний диктант
Запишіть у вигляді многочлена:
квадрат суми двох виразів 2n і 3m;
квадрат різниці двох виразів t і 2s;
добуток суми двох виразів 2m і 3n на їхню різницю;
різницю квадратів виразів 3m і 4n;
різницю квадратів виразів х + у і х – у;
суму квадратів виразів х + у і х – у.
Запишіть у вигляді многочлена:
квадрат суми двох виразів 2n і 3m;
квадрат різниці двох виразів t і 2s;
добуток суми двох виразів 2m і 3n на їхню різницю;
різницю квадратів виразів 3m і 4n;
різницю квадратів виразів х + у і х – у;
суму квадратів виразів х + у і х – у.

Слайд #13
Відповіді:
4n² + 12 nm + 9m²;
t² – 4ts + 4s²;
4m² – 9n²;
9m² – 16n²;
(x+y)²–(x–y)²=(x+y–x+y)(x+y+x–y) = =4xy;
(x+y)²+(x–y)²=x²+2xy+y²+x²–2xy+y² =
=2x²+2y².
4n² + 12 nm + 9m²;
t² – 4ts + 4s²;
4m² – 9n²;
9m² – 16n²;
(x+y)²–(x–y)²=(x+y–x+y)(x+y+x–y) = =4xy;
(x+y)²+(x–y)²=x²+2xy+y²+x²–2xy+y² =
=2x²+2y².

Слайд #14
Куб суми двох виразів
( a + b )³ = a³ + 3a²b + 3ab² + b³
Куб суми двох виразів дорівнює кубу першого виразу плюс потроєний добуток квадрата першого виразу і другого плюс потроєний добуток першого виразу і квадрата другого плюс куб другого виразу.
Приклади: 1) (2 + a)³ = 8 + 12a + 6a² + a³;
2) (x² + 3y)³ = x6 +9x4y +27x²y² +27y3.
Урок 5
( a + b )³ = a³ + 3a²b + 3ab² + b³
Куб суми двох виразів дорівнює кубу першого виразу плюс потроєний добуток квадрата першого виразу і другого плюс потроєний добуток першого виразу і квадрата другого плюс куб другого виразу.
Приклади: 1) (2 + a)³ = 8 + 12a + 6a² + a³;
2) (x² + 3y)³ = x6 +9x4y +27x²y² +27y3.
Урок 5

Слайд #15
Куб різниці двох виразів
( a - b )³ = a³ - 3a²b + 3ab² - b³
Куб різниці двох виразів дорівнює кубу першого виразу мінус потроєний добуток квадрата першого виразу і другого плюс потроєний добуток першого виразу і квадрата другого мінус куб другого виразу.
Приклади: 1) (2 - a)³ = 8 - 12a + 6a² - a³;
2) (x² - 3y)³ = x6 - 9x4y + 27x²y² - 27y3.
( a - b )³ = a³ - 3a²b + 3ab² - b³
Куб різниці двох виразів дорівнює кубу першого виразу мінус потроєний добуток квадрата першого виразу і другого плюс потроєний добуток першого виразу і квадрата другого мінус куб другого виразу.
Приклади: 1) (2 - a)³ = 8 - 12a + 6a² - a³;
2) (x² - 3y)³ = x6 - 9x4y + 27x²y² - 27y3.

Слайд #16
Самостійна робота
1.Піднесіть до куба двочлен:
(a + 2x)³; (3y + b)³;
(4n – 3m)³; (2a – 5x)³;
(-c – 3k)³; (-2n – m)³.
2.Виконайте дії та спростіть:
І в. (y – 3)³ + (3y – 1)(3y + 1);
ІІ в. (x + 2)³ – (2x – 3)(2x + 3).
1.Піднесіть до куба двочлен:
(a + 2x)³; (3y + b)³;
(4n – 3m)³; (2a – 5x)³;
(-c – 3k)³; (-2n – m)³.
2.Виконайте дії та спростіть:
І в. (y – 3)³ + (3y – 1)(3y + 1);
ІІ в. (x + 2)³ – (2x – 3)(2x + 3).

Слайд #17
Розкладання многочленів на множники з використанням формул квадрата суми і квадрата різниці
a² + 2ab + b² = ( a + b )² ;
a² – 2ab + b² = ( a – b )² .
Приклади: 1) 9a² – 24ab + 16b² = (3a – 4b)²;
2) 0,25m² + 2mn + 4n² = (0,5m + 2n)².
Урок 6 – 7
a² + 2ab + b² = ( a + b )² ;
a² – 2ab + b² = ( a – b )² .
Приклади: 1) 9a² – 24ab + 16b² = (3a – 4b)²;
2) 0,25m² + 2mn + 4n² = (0,5m + 2n)².
Урок 6 – 7

Слайд #18
Гра “ Відгадай назву ”
На території Венесуели існує дивовижне плато, на якому ростуть рослини, яких немає в жодному іншому місці земної кулі.
Ні один з дослідників не знав про це плато аж до 1937 року. Влітку його року один венесуельський пілот на своєму літаку випадково потрапив на територію плато і побачив височенний водоспад, висота якого становить 1054 м, тобто в 22 рази більша висоти відомої Ніагари. Іменем пілота пізніше було названо цей водоспад.
Прізвище цього венесуельського пілота зашифровано в наступних завданнях. Правильно розв'язавши завдання, в виділених клітинках Ви зможете прочитати зашифроване слово.
На території Венесуели існує дивовижне плато, на якому ростуть рослини, яких немає в жодному іншому місці земної кулі.
Ні один з дослідників не знав про це плато аж до 1937 року. Влітку його року один венесуельський пілот на своєму літаку випадково потрапив на територію плато і побачив височенний водоспад, висота якого становить 1054 м, тобто в 22 рази більша висоти відомої Ніагари. Іменем пілота пізніше було названо цей водоспад.
Прізвище цього венесуельського пілота зашифровано в наступних завданнях. Правильно розв'язавши завдання, в виділених клітинках Ви зможете прочитати зашифроване слово.

Слайд #19
Ауян Тепуї (“Гора диявола”) – так звуть це плато місцеві індіанці. В цьому районі грози й блискавки протягом літа майже безперервні. Водоспад тут теж має свої особливості. Звичайно водоспади народжуються річками, цей же сам народжує річку.
Завдання. Розкладіть многочлен на множники:
1. p² + 2pq + q² ;
2. 4a² - 4a + 1;
3. 4b² + 12b + 9;
4. 25m² – 20mn + 4n² ;
5. 0,36c² – 0,6cx + 0,25x²;
6. 0,01a² + 4ab² + 400b4.
Зашифроване слово
(p - q)²
О
(2b – 3)²
Д
(2а – 1)²
Н
(0,1a + 40b²)²
С
(p + q)²
А
(0,6c² – 0,5x)²
Р
(0,01a + 20b)²
Б
(2b + 3)²
X
(2а + 1)²
К
(0,6c – 0,5x)²
Л
(5m – 4n)²
У
(0,1a + 20b²)²
Ь
(5m – 2n)²
Е
(0,1a - 20b²)²
П
Завдання. Розкладіть многочлен на множники:
1. p² + 2pq + q² ;
2. 4a² - 4a + 1;
3. 4b² + 12b + 9;
4. 25m² – 20mn + 4n² ;
5. 0,36c² – 0,6cx + 0,25x²;
6. 0,01a² + 4ab² + 400b4.
Зашифроване слово
(p - q)²
О
(2b – 3)²
Д
(2а – 1)²
Н
(0,1a + 40b²)²
С
(p + q)²
А
(0,6c² – 0,5x)²
Р
(0,01a + 20b)²
Б
(2b + 3)²
X
(2а + 1)²
К
(0,6c – 0,5x)²
Л
(5m – 4n)²
У
(0,1a + 20b²)²
Ь
(5m – 2n)²
Е
(0,1a - 20b²)²
П

Слайд #20
Сума кубів двох виразів
a³ + b³ = ( a + b )(a² - ab + b²)
Сума кубів двох виразів дорівнює добутку суми цих виразів і неповного квадрата їх різниці.
Приклади: 1) a³ + 64 =(a + 4)(a² - 4a + 16);
2) 27m³ + 125n³ =(3m + 5n)(9m²-15mn+25n²).
Урок 8 – 9
a³ + b³ = ( a + b )(a² - ab + b²)
Сума кубів двох виразів дорівнює добутку суми цих виразів і неповного квадрата їх різниці.
Приклади: 1) a³ + 64 =(a + 4)(a² - 4a + 16);
2) 27m³ + 125n³ =(3m + 5n)(9m²-15mn+25n²).
Урок 8 – 9

Слайд #21
Різниця кубів двох виразів
a³ - b³ = ( a - b )(a² + ab + b²)
Різниця кубів двох виразів дорівнює добутку різниці цих виразів і неповного квадрата їх суми.
Приклади: 1) a³ – 64 =(a – 4)(a² + 4a + 16);
2) 27m³–125n³=(3m–5n)(9m²+15mn+
+25n²).
a³ - b³ = ( a - b )(a² + ab + b²)
Різниця кубів двох виразів дорівнює добутку різниці цих виразів і неповного квадрата їх суми.
Приклади: 1) a³ – 64 =(a – 4)(a² + 4a + 16);
2) 27m³–125n³=(3m–5n)(9m²+15mn+
+25n²).

Слайд #22
Самостійна робота
Варіант 1
Варіант 2
1) Вставте замість крапок такий вираз, щоб добуток можна було записати у вигляді суми або різниці кубів:
а) (а – 5)(…);
b) (…)(121b² - 11bm + m²);
c) (…+2p)(81q² …).
а) (7 + b)(…);
b) (…)(100a² + 10an + n²);
c) (3k – …)(… 64t²).
2) Подайте у вигляді суми або різниці кубів:
а) (0,1а+2b)(0,01a²-0,2ab+4b²);
b) (5x–7y)(25x²+35xy+49y²).
а) (3а+0,1b)(9a²-0,3ab+0,01b²);
b) (3x–11y)(9x²+33xy+121y²).
3) Спростіть вираз:
(x+5)(x²–5x+25)+5(x–5)(x+5).
x(x+8)(x–8)–(x–4)(x²+4x+ 16).
4) Розв'яжіть рівняння:
(3x+1)(9x²–3x+1)–x²(27x+1)=0.
(x–3)(x²+3x+9)–x²(x+1)+52=0.
Варіант 1
Варіант 2
1) Вставте замість крапок такий вираз, щоб добуток можна було записати у вигляді суми або різниці кубів:
а) (а – 5)(…);
b) (…)(121b² - 11bm + m²);
c) (…+2p)(81q² …).
а) (7 + b)(…);
b) (…)(100a² + 10an + n²);
c) (3k – …)(… 64t²).
2) Подайте у вигляді суми або різниці кубів:
а) (0,1а+2b)(0,01a²-0,2ab+4b²);
b) (5x–7y)(25x²+35xy+49y²).
а) (3а+0,1b)(9a²-0,3ab+0,01b²);
b) (3x–11y)(9x²+33xy+121y²).
3) Спростіть вираз:
(x+5)(x²–5x+25)+5(x–5)(x+5).
x(x+8)(x–8)–(x–4)(x²+4x+ 16).
4) Розв'яжіть рівняння:
(3x+1)(9x²–3x+1)–x²(27x+1)=0.
(x–3)(x²+3x+9)–x²(x+1)+52=0.

Слайд #23
Тест 1 “Формули скороченого множення. Множення многочленів.”
1. (5a + 3b)(5a – 3b) = …
a) 5a² - 3b²; б) 25a² + 9b²; в) 5a² + 3b²; г) 25a² - 9b².
2. (7a + 2)² = …
a) 49a² + 28a + 4; б) 49a² + 14a + 4; в) 49a² + 4; г) 7a² + 28a + 4.
3. (9a – b)² = …
a) 81a² - 9ab + b²; б) 81a² - b²; в) 81a² - 18ab + b²; г) 9a² - 18ab + b².
4. (a + 7)(a² - 7a + 49) = …
a) a³ - 343; б) a² - 49; в) a³ + 343; г) a³ + 7.
5. (c - 8)(c² + 8c + 64) = …
a) c³ - 512; б) c² - 64; в) c³ + 512; г) c³ - 8.
6. (- b² + 4)(b² + 4) = …
a) 16 - b²; б) b4 - 16; в) b² - 16; г) 16 - b4.
7. (a² + 1)(a + 1)(a - 1) = …
a) a² - 1; б) a4 - 1; в) a² - 2; г) a4 - 2.
8. (- 6a – 5b)² = …
a) -36a² - 60ab - 25b²; б) -36a² + 60ab - 25b²;
в) 36a² + 60ab + 25b²; г) 36a² + 30ab + 25b².
9. (5a - 4b)(5a + 4b) - (3a + 2b)(3a –2b) = …
a) 2a² - 2b²; б) 16a² - 12b²; в) 16a² - 20b²; г) 34a² - 20b².
10. 5,02 · 4,98 = …
a) 24,98; б) 24,96; в) 20; г) 24,9996.
1. (5a + 3b)(5a – 3b) = …
a) 5a² - 3b²; б) 25a² + 9b²; в) 5a² + 3b²; г) 25a² - 9b².
2. (7a + 2)² = …
a) 49a² + 28a + 4; б) 49a² + 14a + 4; в) 49a² + 4; г) 7a² + 28a + 4.
3. (9a – b)² = …
a) 81a² - 9ab + b²; б) 81a² - b²; в) 81a² - 18ab + b²; г) 9a² - 18ab + b².
4. (a + 7)(a² - 7a + 49) = …
a) a³ - 343; б) a² - 49; в) a³ + 343; г) a³ + 7.
5. (c - 8)(c² + 8c + 64) = …
a) c³ - 512; б) c² - 64; в) c³ + 512; г) c³ - 8.
6. (- b² + 4)(b² + 4) = …
a) 16 - b²; б) b4 - 16; в) b² - 16; г) 16 - b4.
7. (a² + 1)(a + 1)(a - 1) = …
a) a² - 1; б) a4 - 1; в) a² - 2; г) a4 - 2.
8. (- 6a – 5b)² = …
a) -36a² - 60ab - 25b²; б) -36a² + 60ab - 25b²;
в) 36a² + 60ab + 25b²; г) 36a² + 30ab + 25b².
9. (5a - 4b)(5a + 4b) - (3a + 2b)(3a –2b) = …
a) 2a² - 2b²; б) 16a² - 12b²; в) 16a² - 20b²; г) 34a² - 20b².
10. 5,02 · 4,98 = …
a) 24,98; б) 24,96; в) 20; г) 24,9996.

Слайд #24
Урок 10
Вивчення математики подібне до Нілу, що починається невеликим струмком, а закінчується великою річкою.
Ч.К. Колтон.
Вивчення математики подібне до Нілу, що починається невеликим струмком, а закінчується великою річкою.
Ч.К. Колтон.

Слайд #25
Розкладання многочленів на множники способом винесення спільного множника за дужки
ab + ac = a(b + c)
Алгоритм
Розкласти кожен член многочлена на множники так, щоб серед них був спільний множник.
Застосувати розподільний закон множення відносно алгебраїчної суми: виділений спільний множник помножити на суму множників, які залишилися, записавши її в дужках.
Приклади: 1) 4a + 12 = 4(a +3);
2) 12x³y – 18x²y² = 6x²y(2x – 3y);
3) 5b(a – c) + 7(a – c) = (a – c)(5b + 7).
ab + ac = a(b + c)
Алгоритм
Розкласти кожен член многочлена на множники так, щоб серед них був спільний множник.
Застосувати розподільний закон множення відносно алгебраїчної суми: виділений спільний множник помножити на суму множників, які залишилися, записавши її в дужках.
Приклади: 1) 4a + 12 = 4(a +3);
2) 12x³y – 18x²y² = 6x²y(2x – 3y);
3) 5b(a – c) + 7(a – c) = (a – c)(5b + 7).

Слайд #26
Розкладання многочленів на множники способом групування
ax + ay + bx + by = a(х+y) + b(x+y) =
= (x + y)(a + b)
Алгоритм
Об'єднати члени многочлена в такі групи, які мають спільний множник у вигляді многочлена.
Винести цей спільний множник за дужки.
Приклади: 1) 6m – 6n + am – an = 6(m – n) +
+ a(m – n) = (m – n)(6 + a);
2) 3a²c + 6a² – 10bc – 5bc² = 3a²(c +2) –
–5bc(2 + c) = (c +2)(3a² – 5bc).
ax + ay + bx + by = a(х+y) + b(x+y) =
= (x + y)(a + b)
Алгоритм
Об'єднати члени многочлена в такі групи, які мають спільний множник у вигляді многочлена.
Винести цей спільний множник за дужки.
Приклади: 1) 6m – 6n + am – an = 6(m – n) +
+ a(m – n) = (m – n)(6 + a);
2) 3a²c + 6a² – 10bc – 5bc² = 3a²(c +2) –
–5bc(2 + c) = (c +2)(3a² – 5bc).

Слайд #27
Застосування кількох способів для розкладання многочленів на множники
Алгоритм
1. Винести спільний множник (якщо він є) за дужки.
2. Спробувати розкласти многочлен на множники за допомогою формул скороченого множення.
3. Застосувати спосіб групування (якщо попередні способи не привели до мети).
Урок 11 - 12
Алгоритм
1. Винести спільний множник (якщо він є) за дужки.
2. Спробувати розкласти многочлен на множники за допомогою формул скороченого множення.
3. Застосувати спосіб групування (якщо попередні способи не привели до мети).
Урок 11 - 12

Слайд #28
Застосування кількох способів для розкладання многочленів на множники
Приклади:
1. 7a²b² – 7b4 = 7b²(a² – b²) =
= 7b²(a – b)(a + b);
2. 6ac – 9c – 24abc + 36bc =
= 3c(2a – 3 – 8ab +12b) =
= 3c((2a–3) – 4b(2a–3)) =
= 3c(2a–3)(1–4b);
Приклади:
1. 7a²b² – 7b4 = 7b²(a² – b²) =
= 7b²(a – b)(a + b);
2. 6ac – 9c – 24abc + 36bc =
= 3c(2a – 3 – 8ab +12b) =
= 3c((2a–3) – 4b(2a–3)) =
= 3c(2a–3)(1–4b);

Слайд #29
Застосування кількох способів для розкладання многочленів на множники
3. x² – 6x – 16 = x² – 6x + 9 – 9 –16 =
= (x – 3)² – 25 = (x–3–5)(x–3+5) =
= (x – 8)(x + 2);
4. x² – 2xy + y² – z² = (x–y)² – z² =
= (x – y – z)(x – y + z).
3. x² – 6x – 16 = x² – 6x + 9 – 9 –16 =
= (x – 3)² – 25 = (x–3–5)(x–3+5) =
= (x – 8)(x + 2);
4. x² – 2xy + y² – z² = (x–y)² – z² =
= (x – y – z)(x – y + z).

Слайд #30
Логічна вправа
Вставте пропущені вирази, розклавши многочлени на множники:
a² - 25b²
3p² + 6pq + 3q²
2a³ - 16b³
x² - xy + ax - ay
?
a + 5b
?
?
?
?
?
?
?
?
?
?
3mn + 24n – 9m – 72
m – 10m² + 25m³
Вставте пропущені вирази, розклавши многочлени на множники:
a² - 25b²
3p² + 6pq + 3q²
2a³ - 16b³
x² - xy + ax - ay
?
a + 5b
?
?
?
?
?
?
?
?
?
?
3mn + 24n – 9m – 72
m – 10m² + 25m³

Слайд #31
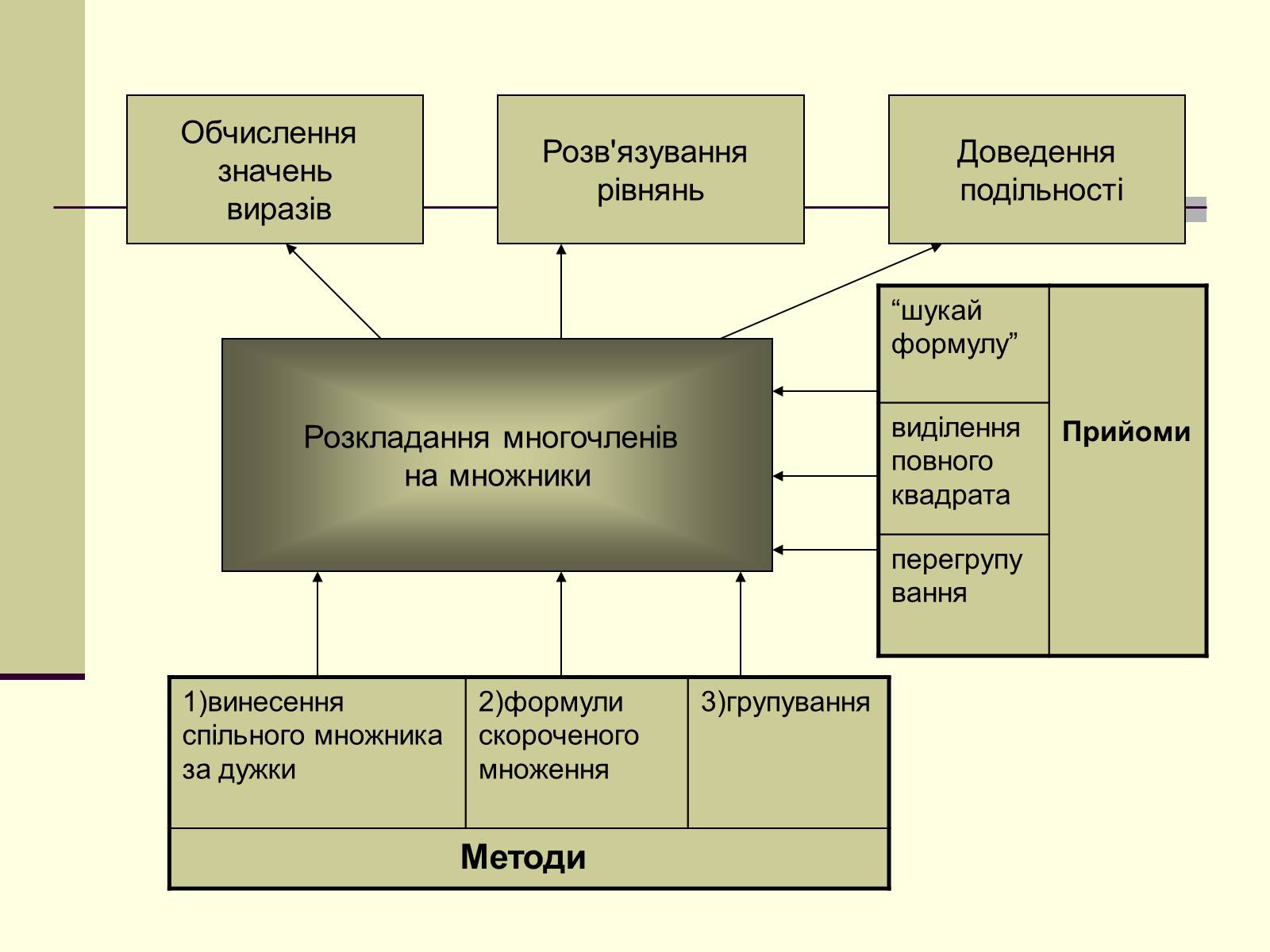
1)винесення спільного множника за дужки
2)формули скороченого множення
3)групування
Методи
Розкладання многочленів
на множники
Обчислення
значень
виразів
Розв'язування
рівнянь
Доведення
подільності
“шукай формулу”
Прийоми
виділення повного квадрата
перегрупування
2)формули скороченого множення
3)групування
Методи
Розкладання многочленів
на множники
Обчислення
значень
виразів
Розв'язування
рівнянь
Доведення
подільності
“шукай формулу”
Прийоми
виділення повного квадрата
перегрупування
Слайд #32
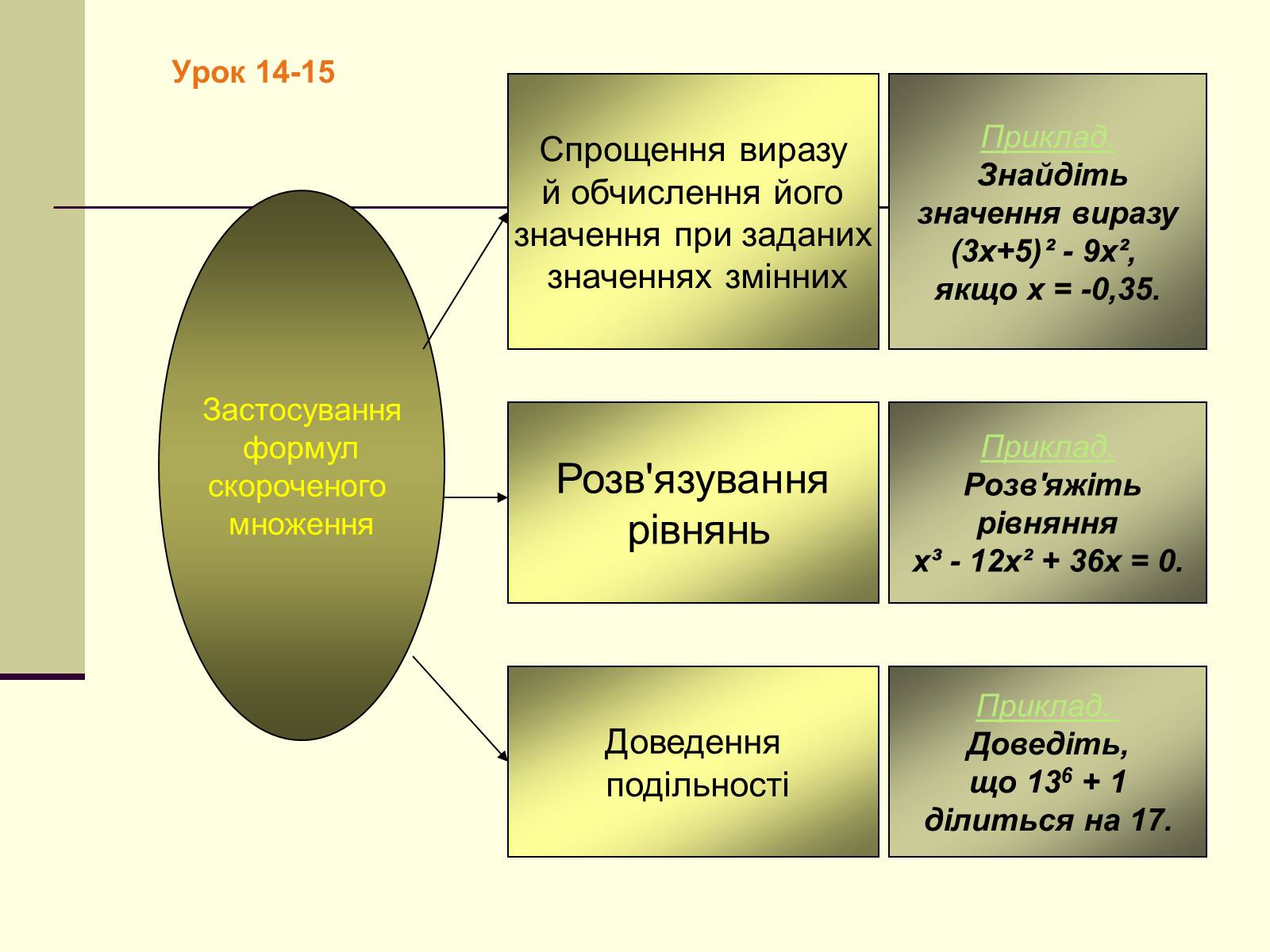
Урок 14-15
Застосування
формул
скороченого
множення
Приклад.
Розв'яжіть
рівняння
х³ - 12х² + 36х = 0.
Розв'язування
рівнянь
Спрощення виразу
й обчислення його
значення при заданих
значеннях змінних
Доведення
подільності
Приклад.
Доведіть,
що 136 + 1
ділиться на 17.
Приклад.
Знайдіть
значення виразу
(3х+5)² - 9х²,
якщо х = -0,35.
Застосування
формул
скороченого
множення
Приклад.
Розв'яжіть
рівняння
х³ - 12х² + 36х = 0.
Розв'язування
рівнянь
Спрощення виразу
й обчислення його
значення при заданих
значеннях змінних
Доведення
подільності
Приклад.
Доведіть,
що 136 + 1
ділиться на 17.
Приклад.
Знайдіть
значення виразу
(3х+5)² - 9х²,
якщо х = -0,35.
Слайд #33
Тест 2 “ Формули скороченого множення. Розкладання на множники.”
1. a² - 169 = …
a) (13 – a)(13 + a); б) (a – 13)(a + 13); в) (a – 13)(a – 13); г) a(a – 169).
2. Якщо a>0, b>0 і a² + 2ab + b² = 49, то a + b = …
a) -7; б) 2401; в) 9; г) 7.
3. a² - 18a + 81 = …
a) (a - 3)²; б) a – 9; в) (a – 9)²; г) (a – 9)(a + 9).
4. a³ + 125 = …
a) (a – 5)(a² + 5a + 25); б) (a + 5)(a² - 5a + 25);
в) (a + 5)(a² - 10a + 25); г) (a + 5)(a - 25);
5. a10 - a8 = …
a) a8(a + 1)(a – 1); б) a8(a – 1); в) a8(a +1); г) a8(a + 1)².
6. 64a30 - 80a15b 16 + 25b32 = …
a) (8a15 – 5b30) 2; б) (4a15 – 5b16) 2; в) (8a28 – 5b30) 2; г) (8a15 – 5b16) 2.
7. 6a² + 36a + 54 = …
a) 36(a + 3)²; б) 6(a – 3)(a + 3); в) 6(a – 3)²; г) 6(a + 3)².
8. - 64 + c² = …
a) (8 – c)(8 + c); б) (4 – c)(4 + c); в) (c – 8)(c + 8); г) (c – 4)(c + 4).
9. a² – 49 + a – 7 = …
a) (a – 8)(a + 7); б) (a – 7)(a + 8); в) (a – 7)(a + 6); г) (a + 7)(a + 6).
10. b² – a² – 22a – 121 = …
a) (b – a – 11)(b + a + 11); б) (b – a + 11)(b + a + 11);
в) (b + a – 11)(b + a + 11); г) (a – b – 11)(b + a + 11).
1. a² - 169 = …
a) (13 – a)(13 + a); б) (a – 13)(a + 13); в) (a – 13)(a – 13); г) a(a – 169).
2. Якщо a>0, b>0 і a² + 2ab + b² = 49, то a + b = …
a) -7; б) 2401; в) 9; г) 7.
3. a² - 18a + 81 = …
a) (a - 3)²; б) a – 9; в) (a – 9)²; г) (a – 9)(a + 9).
4. a³ + 125 = …
a) (a – 5)(a² + 5a + 25); б) (a + 5)(a² - 5a + 25);
в) (a + 5)(a² - 10a + 25); г) (a + 5)(a - 25);
5. a10 - a8 = …
a) a8(a + 1)(a – 1); б) a8(a – 1); в) a8(a +1); г) a8(a + 1)².
6. 64a30 - 80a15b 16 + 25b32 = …
a) (8a15 – 5b30) 2; б) (4a15 – 5b16) 2; в) (8a28 – 5b30) 2; г) (8a15 – 5b16) 2.
7. 6a² + 36a + 54 = …
a) 36(a + 3)²; б) 6(a – 3)(a + 3); в) 6(a – 3)²; г) 6(a + 3)².
8. - 64 + c² = …
a) (8 – c)(8 + c); б) (4 – c)(4 + c); в) (c – 8)(c + 8); г) (c – 4)(c + 4).
9. a² – 49 + a – 7 = …
a) (a – 8)(a + 7); б) (a – 7)(a + 8); в) (a – 7)(a + 6); г) (a + 7)(a + 6).
10. b² – a² – 22a – 121 = …
a) (b – a – 11)(b + a + 11); б) (b – a + 11)(b + a + 11);
в) (b + a – 11)(b + a + 11); г) (a – b – 11)(b + a + 11).

Слайд #34
Історична довідка
Формули скороченого множення стародавнім китайським і грецьким математикам були відомі за багато віків до початку нашої ери. Записували їх тоді не за допомогою букв, а словами, і доводили геометрично (тільки для додатних чисел). Користуючись малюнком, пояснювали, що для будь-яких чисел a і b площа квадрата із стороною a + b дорівнює сумі площ двох квадратів із сторонами a і b і двох прямокутників із сторонами a, b. Отже, (a + b)² = a² + 2ab + b². Подібним способом обґрунтували й інші рівності, які тепер ми називаємо формулами скороченого множення.
Формули скороченого множення стародавнім китайським і грецьким математикам були відомі за багато віків до початку нашої ери. Записували їх тоді не за допомогою букв, а словами, і доводили геометрично (тільки для додатних чисел). Користуючись малюнком, пояснювали, що для будь-яких чисел a і b площа квадрата із стороною a + b дорівнює сумі площ двох квадратів із сторонами a і b і двох прямокутників із сторонами a, b. Отже, (a + b)² = a² + 2ab + b². Подібним способом обґрунтували й інші рівності, які тепер ми називаємо формулами скороченого множення.

Слайд #35
Багато чого з математики
не залишається в пам'яті,
але коли зрозумієш її, тоді
легко при нагоді згадати
призабуте.
М.В. Остроградський.
не залишається в пам'яті,
але коли зрозумієш її, тоді
легко при нагоді згадати
призабуте.
М.В. Остроградський.
