- Головна
- Готові шкільні презентації
- Презентація на тему «Інтеграл»
Презентація на тему «Інтеграл»
2465
Слайд #1
МІНІ
ПІДРУЧНИК
Інтеграл та
його застосування
11КЛАС
Ананьєва
Поліна
ПІДРУЧНИК
Інтеграл та
його застосування
11КЛАС
Ананьєва
Поліна

Слайд #2
Зміст
Означення
Таблиця невизначених інтегралів
Диференціювання та інтегрування
Властивість первісної
Правила знаходження
первісної
Криволінійна трапеція та
її площа
Визначений інтеграл
Формула
Ньютона - Лейбніца
Тести та завдання
Означення
Таблиця невизначених інтегралів
Диференціювання та інтегрування
Властивість первісної
Правила знаходження
первісної
Криволінійна трапеція та
її площа
Визначений інтеграл
Формула
Ньютона - Лейбніца
Тести та завдання

Слайд #3
Означення
Функція F(x) називається первісною для функції f(x) на даному проміжку, якщо для будь-якого х з цього проміжку
Перейти до змісту
Функція F(x) називається первісною для функції f(x) на даному проміжку, якщо для будь-якого х з цього проміжку
Перейти до змісту

Слайд #4
Таблиця первісних (невизначених інтегралів)
Функція f(x)
Загальний вигляд первісних F(x)+С, де С - стала
Запис за допомогою невизначеного інтеграла
С
1
х+С
Перейти до змісту
Функція f(x)
Загальний вигляд первісних F(x)+С, де С - стала
Запис за допомогою невизначеного інтеграла
С
1
х+С
Перейти до змісту

Слайд #5
Операція знаходження
Похідної функції-
диференціювання
Первісної функції-
інтегрування
Диференціювання функції f(x) – операція знаходження її похідної .
Наприклад. Знайти похідну функції:
а) ; б) .
Розв'язання
а) ;
б) .
Знаходження функції f(x) за даною її похідною F(x) називається операцією інтегрування.
Операція інтегрування обернена до операції диференціювання.
Наприклад.
а) Якщо , то , оскільки .
б) Якщо , то ,
оскільки .
Перейти до змісту
Похідної функції-
диференціювання
Первісної функції-
інтегрування
Диференціювання функції f(x) – операція знаходження її похідної .
Наприклад. Знайти похідну функції:
а) ; б) .
Розв'язання
а) ;
б) .
Знаходження функції f(x) за даною її похідною F(x) називається операцією інтегрування.
Операція інтегрування обернена до операції диференціювання.
Наприклад.
а) Якщо , то , оскільки .
б) Якщо , то ,
оскільки .
Перейти до змісту

Слайд #6
Якщо F(x)
первісна для f(x)
Основна властивість первісної
Геометрична інтерпретація основної властивості первісної
Кожна із функцій y=2x2; y=2x2+2; y=2x2-2 є первісною для функції y=4x
Графіки всіх первісних даної функції можна одержати з будь якого шляхом паралельного перенесення вздовж осі оy
F(x)+c –загальний вигляд первісної для f(x)
то
F(x)+c-первісна для f(x)
C-довільна стала
1
2
-1
-2
-1
1
Перейти до змісту
первісна для f(x)
Основна властивість первісної
Геометрична інтерпретація основної властивості первісної
Кожна із функцій y=2x2; y=2x2+2; y=2x2-2 є первісною для функції y=4x
Графіки всіх первісних даної функції можна одержати з будь якого шляхом паралельного перенесення вздовж осі оy
F(x)+c –загальний вигляд первісної для f(x)
то
F(x)+c-первісна для f(x)
C-довільна стала
1
2
-1
-2
-1
1
Перейти до змісту
Слайд #7
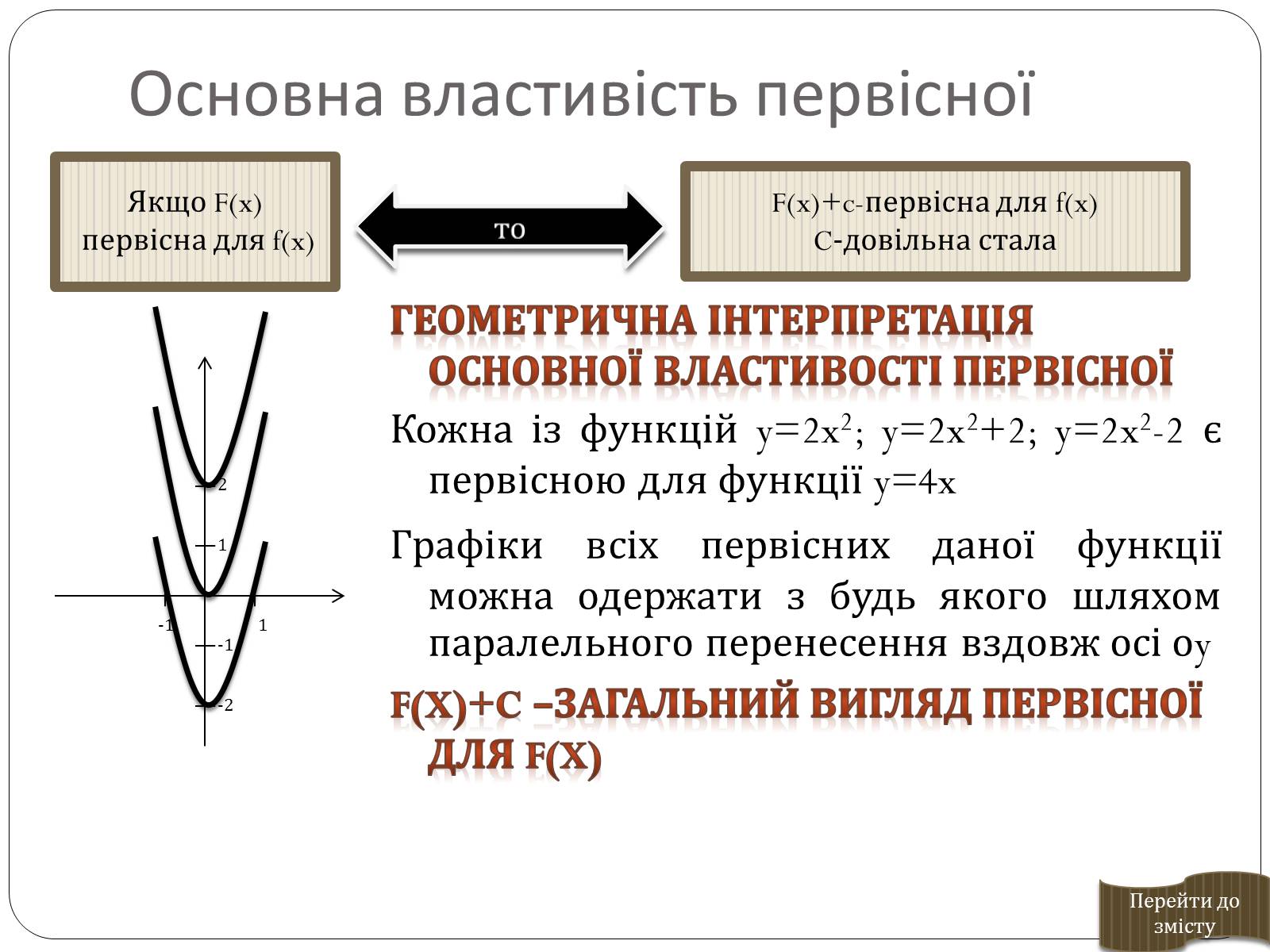
Три правила знаходження первісної
Якщо
F-первісна для f,
H-первісна для h
Якщо
F-первісна для f
Якщо
F(x) - первісна для f(x)
то
то
то
F+H-первісна для f+h
kF-первісна для k∙f;k=const.
F(kx+b)-первісна для f(kx+b);
k і b-сталі;k≠0
Перейти до змісту
Якщо
F-первісна для f,
H-первісна для h
Якщо
F-первісна для f
Якщо
F(x) - первісна для f(x)
то
то
то
F+H-первісна для f+h
kF-первісна для k∙f;k=const.
F(kx+b)-первісна для f(kx+b);
k і b-сталі;k≠0
Перейти до змісту
Слайд #8
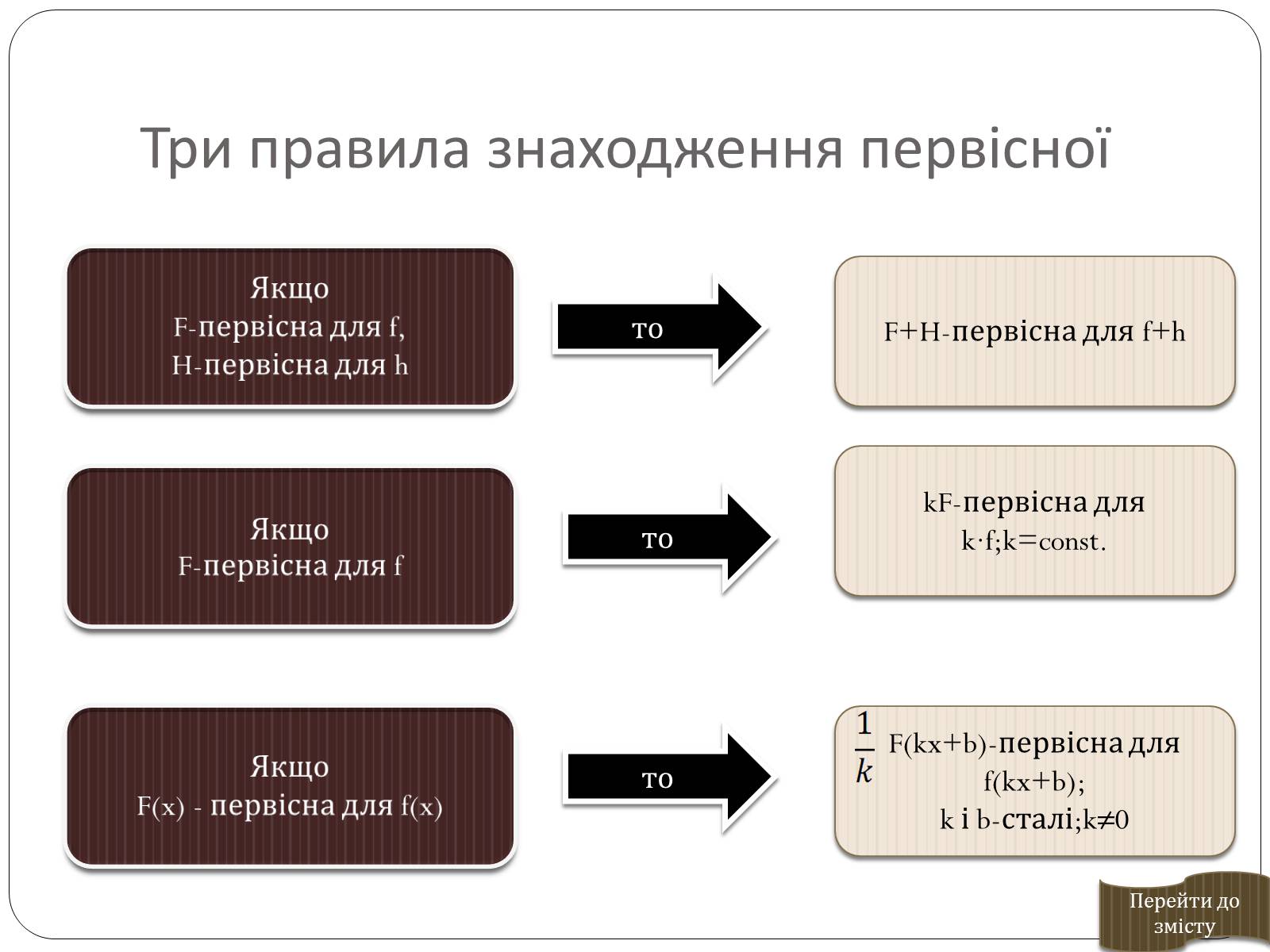
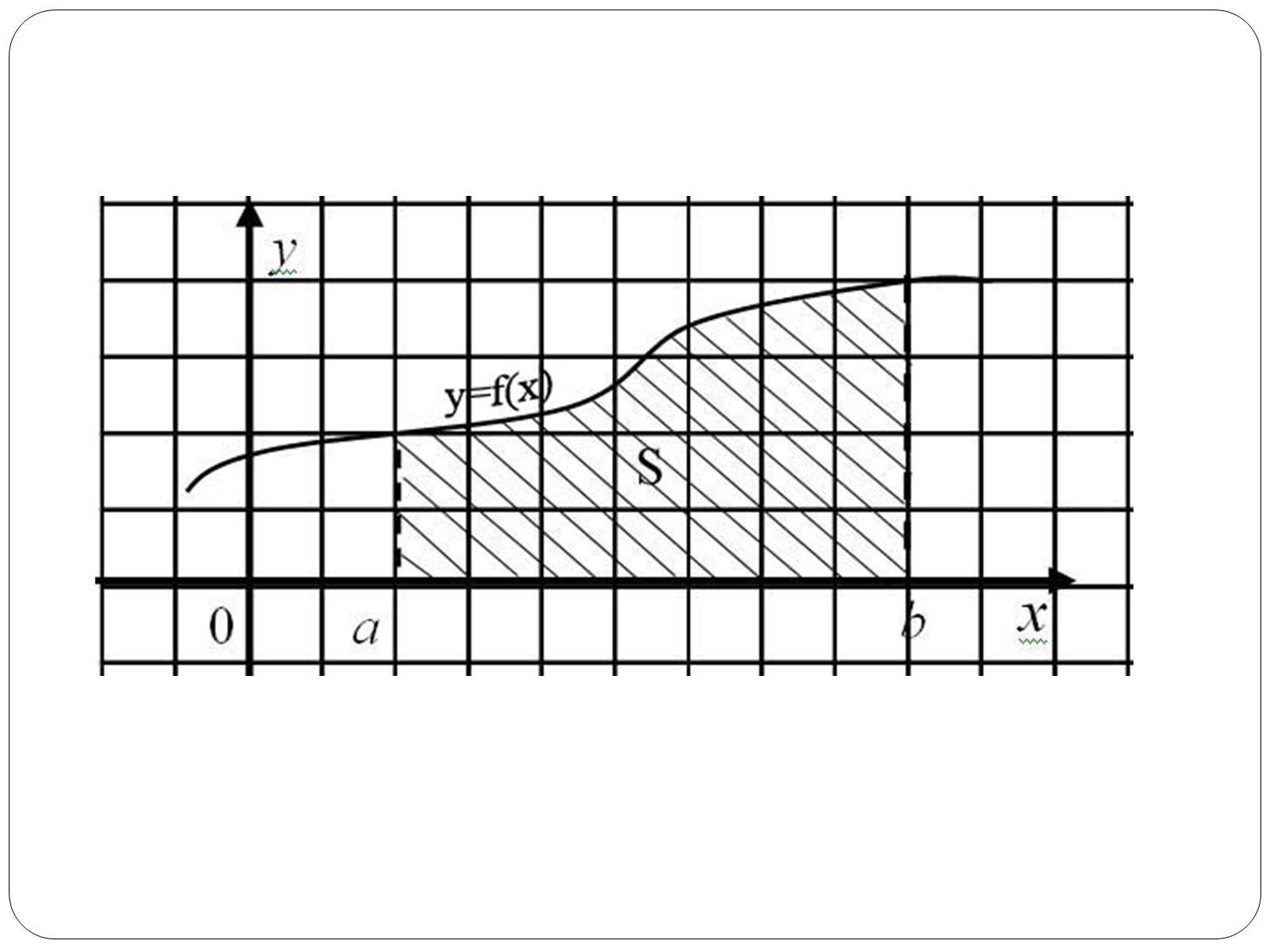
Криволінійна трапеція та її площа
Криволінійною трапецією називається фігура, обмежена графіком невід'ємної на відрізку функції, віссю Ох і прямими x=a і x=b.
Наприклад.
Теорема. Нехай - непарна і невід'ємна на відрізку функція, а S – площа відповідної криволінійної трапеції.
Якщо - первісна для на інтервалі, що містить відрізок , то .
Наприклад. Обчислити площу криволінійної трапеції, обмеженої лініями: , , x=0, .
Розв'язання
- синусоїда; - вісь Ox; x=0 – вісь Оу; - пряма, що проходить через
точку паралельно осі Оу.
Для функції первісною є a=0, b = .
Нехай S - шукана площа, тоді .
(кв. од.)
Відповідь: 2 кв. од.
Перейти до змісту
Криволінійною трапецією називається фігура, обмежена графіком невід'ємної на відрізку функції, віссю Ох і прямими x=a і x=b.
Наприклад.
Теорема. Нехай - непарна і невід'ємна на відрізку функція, а S – площа відповідної криволінійної трапеції.
Якщо - первісна для на інтервалі, що містить відрізок , то .
Наприклад. Обчислити площу криволінійної трапеції, обмеженої лініями: , , x=0, .
Розв'язання
- синусоїда; - вісь Ox; x=0 – вісь Оу; - пряма, що проходить через
точку паралельно осі Оу.
Для функції первісною є a=0, b = .
Нехай S - шукана площа, тоді .
(кв. од.)
Відповідь: 2 кв. од.
Перейти до змісту
Слайд #9
Площа криволінійної трапеції
S – площа криволінійної трапеції;
F (x) – будь-яка первісна функції f(x) на відрізку
[a; b].
Площу S криволінійної трапеції, обмеженої графіком функції y=f(x) і прямими y=0, x=a i x=b (aS = F(b) – F(a)
S – площа криволінійної трапеції;
F (x) – будь-яка первісна функції f(x) на відрізку
[a; b].
Площу S криволінійної трапеції, обмеженої графіком функції y=f(x) і прямими y=0, x=a i x=b (a

Слайд #10
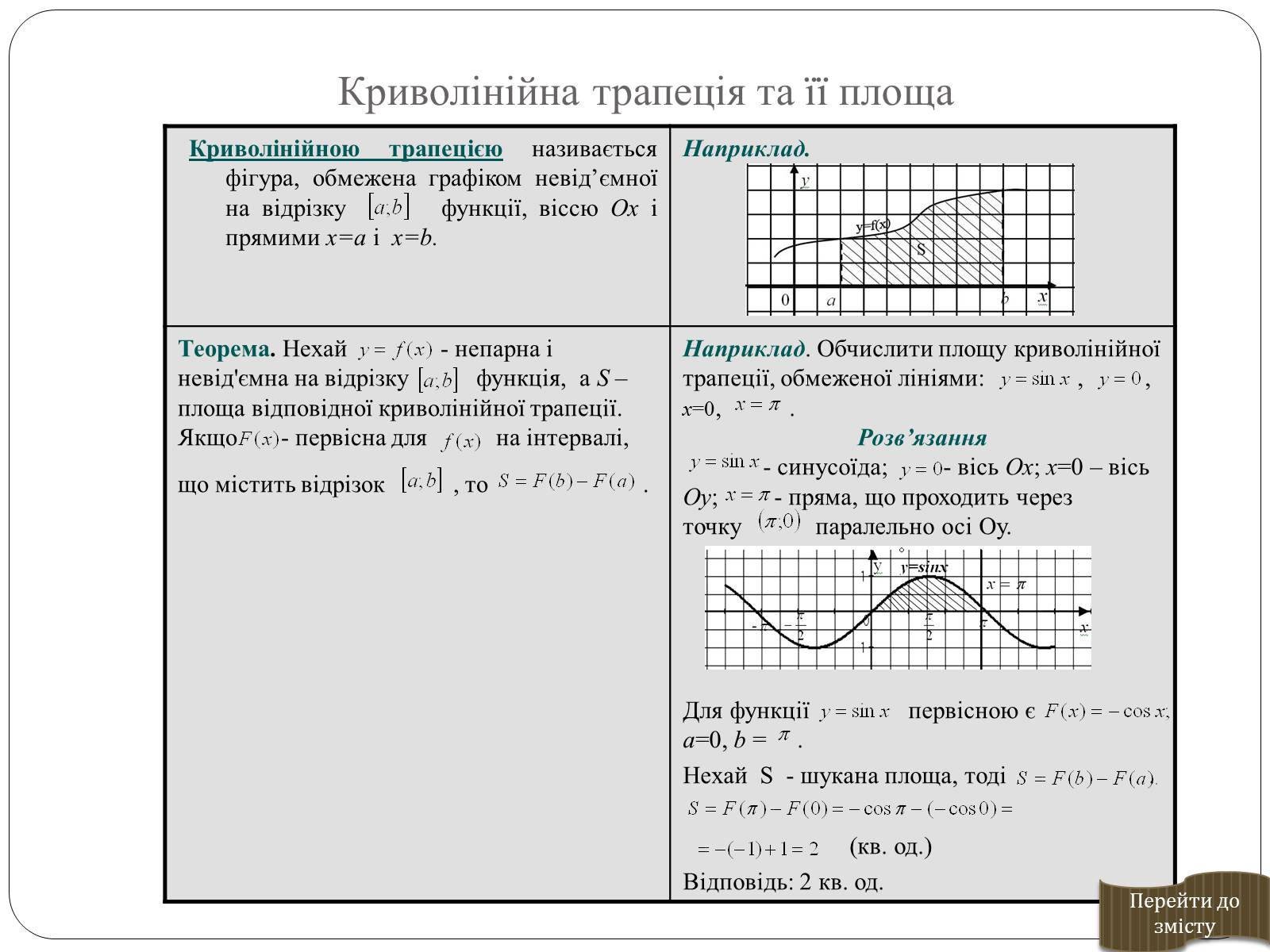
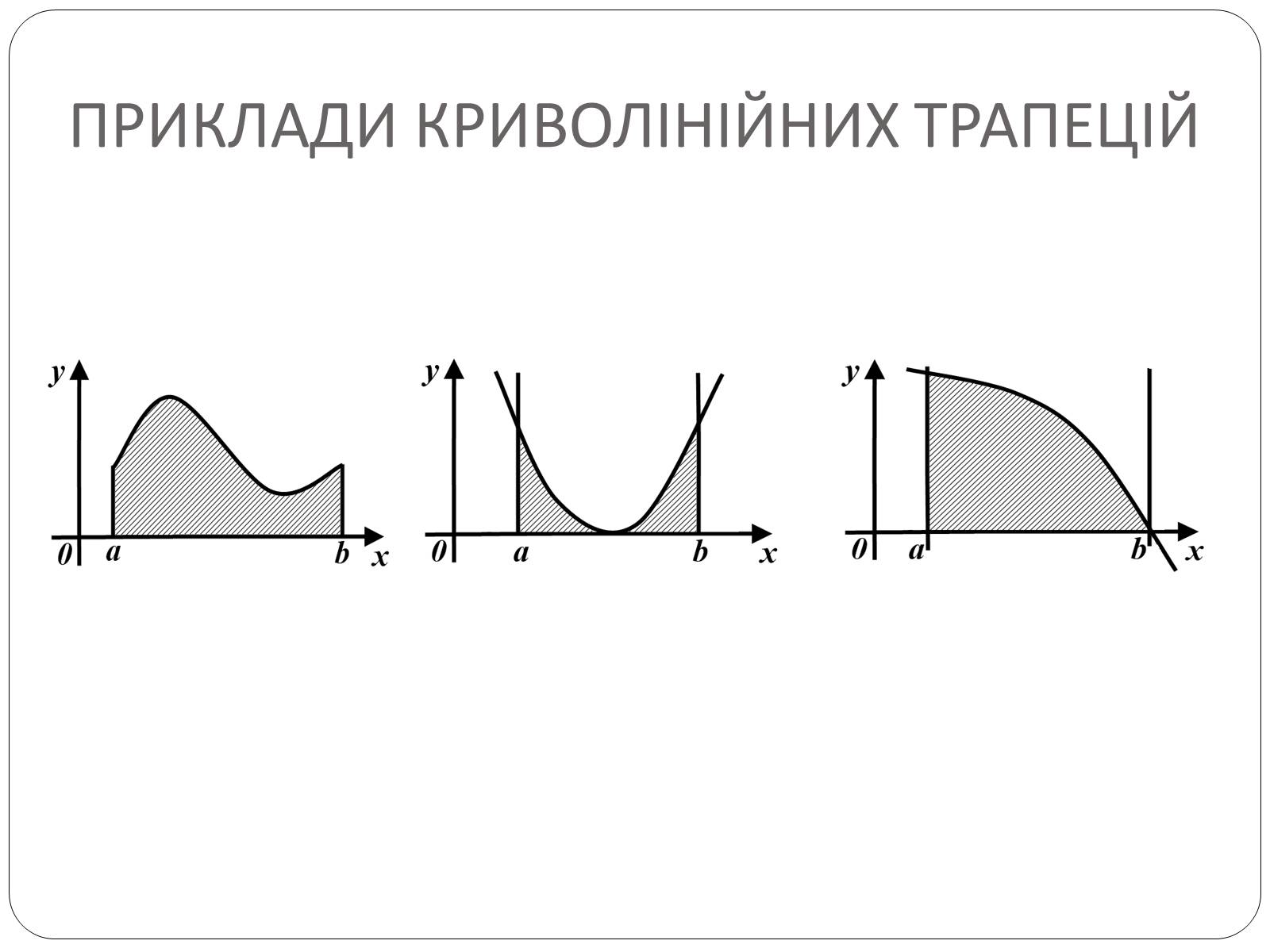
Приклади криволінійних трапецій
Слайд #11
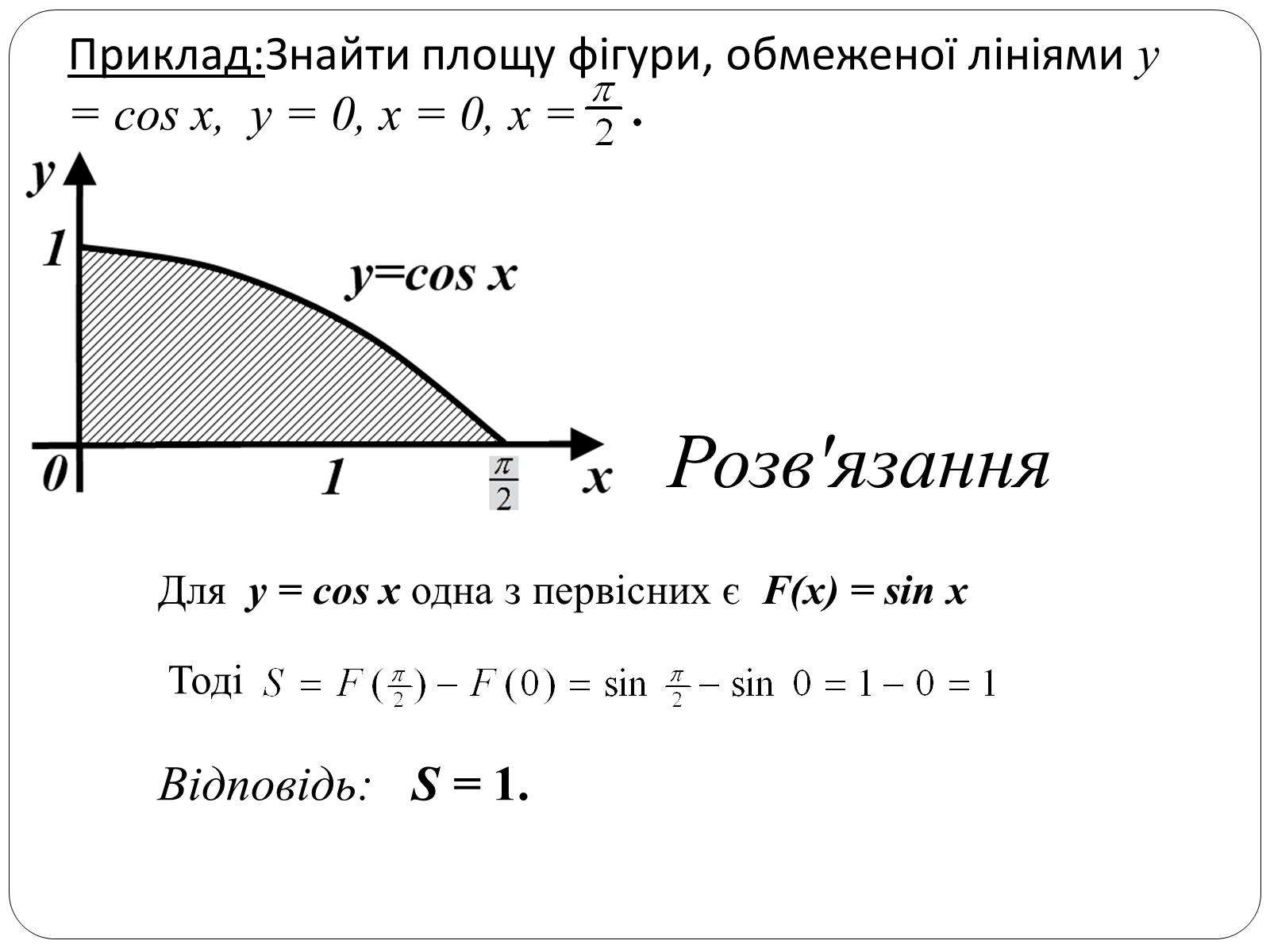
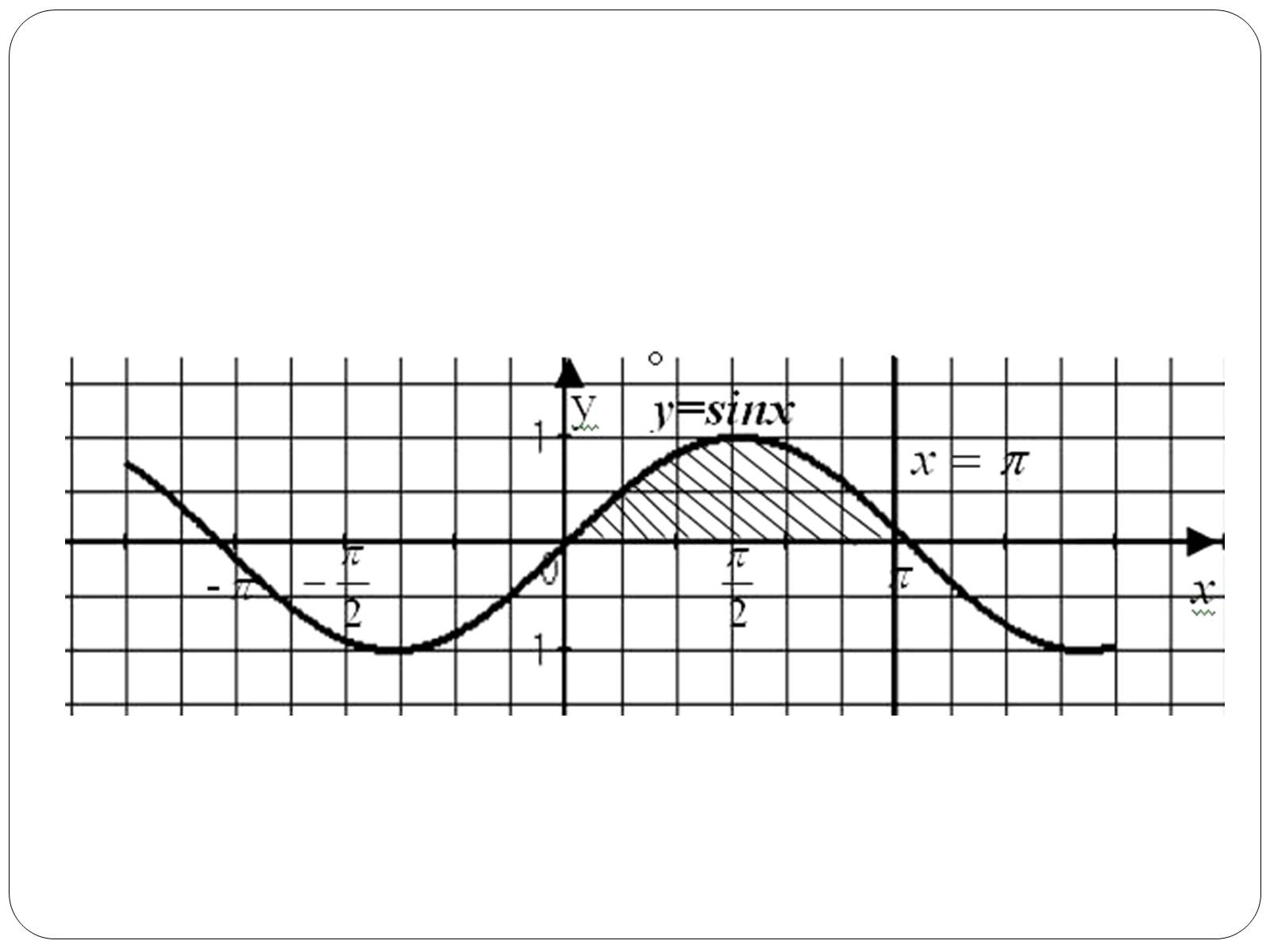
Приклад:Знайти площу фігури, обмеженої лініями y = cos x, y = 0, x = 0, x =
Розв'язання
Для y = cos x одна з первісних є F(x) = sin x
Тоді
Відповідь: S = 1.
Розв'язання
Для y = cos x одна з первісних є F(x) = sin x
Тоді
Відповідь: S = 1.
Слайд #12
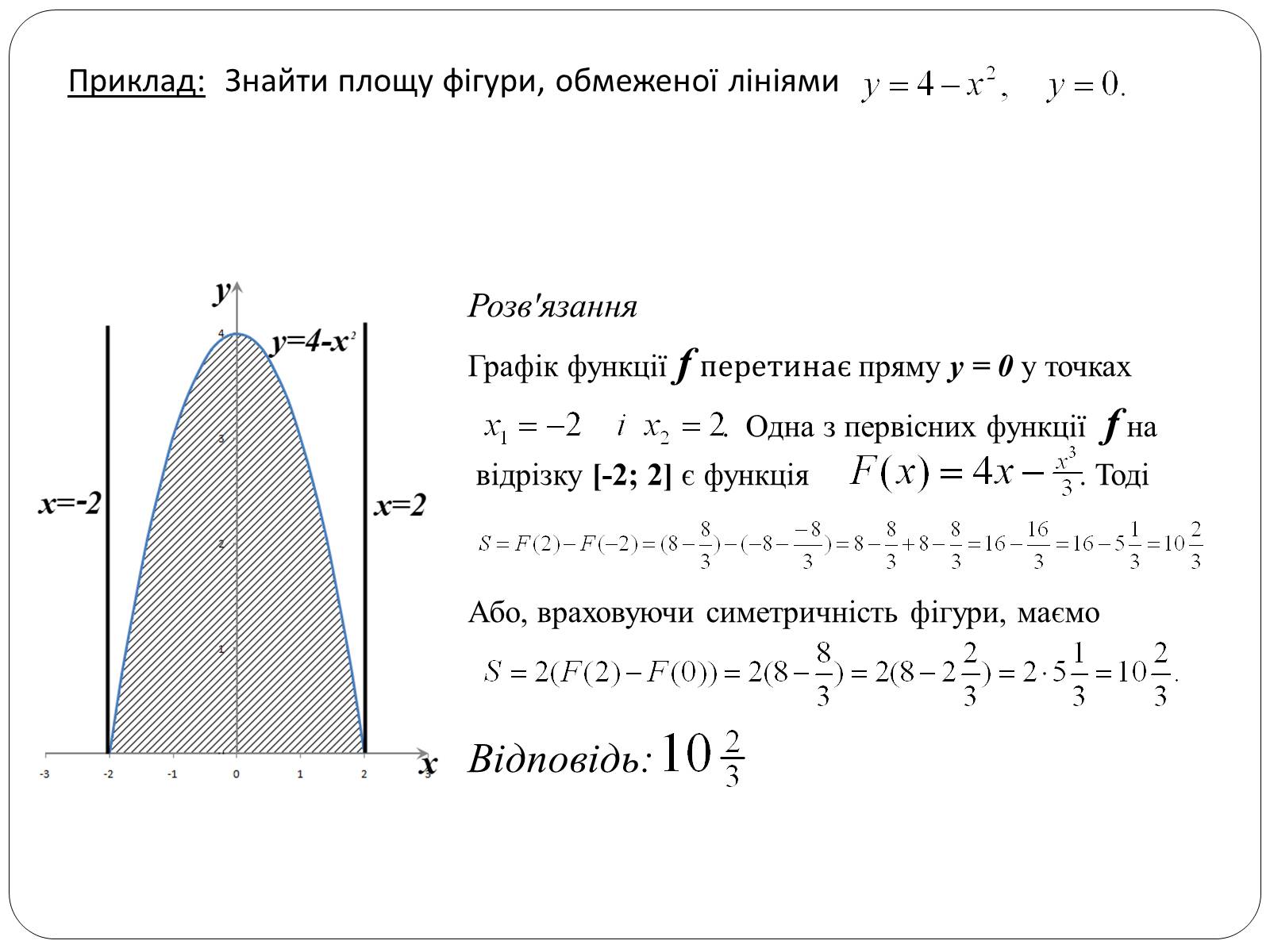
Приклад: Знайти площу фігури, обмеженої лініями
Розв'язання
Графік функції f перетинає пряму y = 0 у точках
. Одна з первісних функції f на
відрізку [-2; 2] є функція tt . Тоді
Або, враховуючи симетричність фігури, маємо
Відповідь:
Розв'язання
Графік функції f перетинає пряму y = 0 у точках
. Одна з первісних функції f на
відрізку [-2; 2] є функція tt . Тоді
Або, враховуючи симетричність фігури, маємо
Відповідь:
Слайд #13
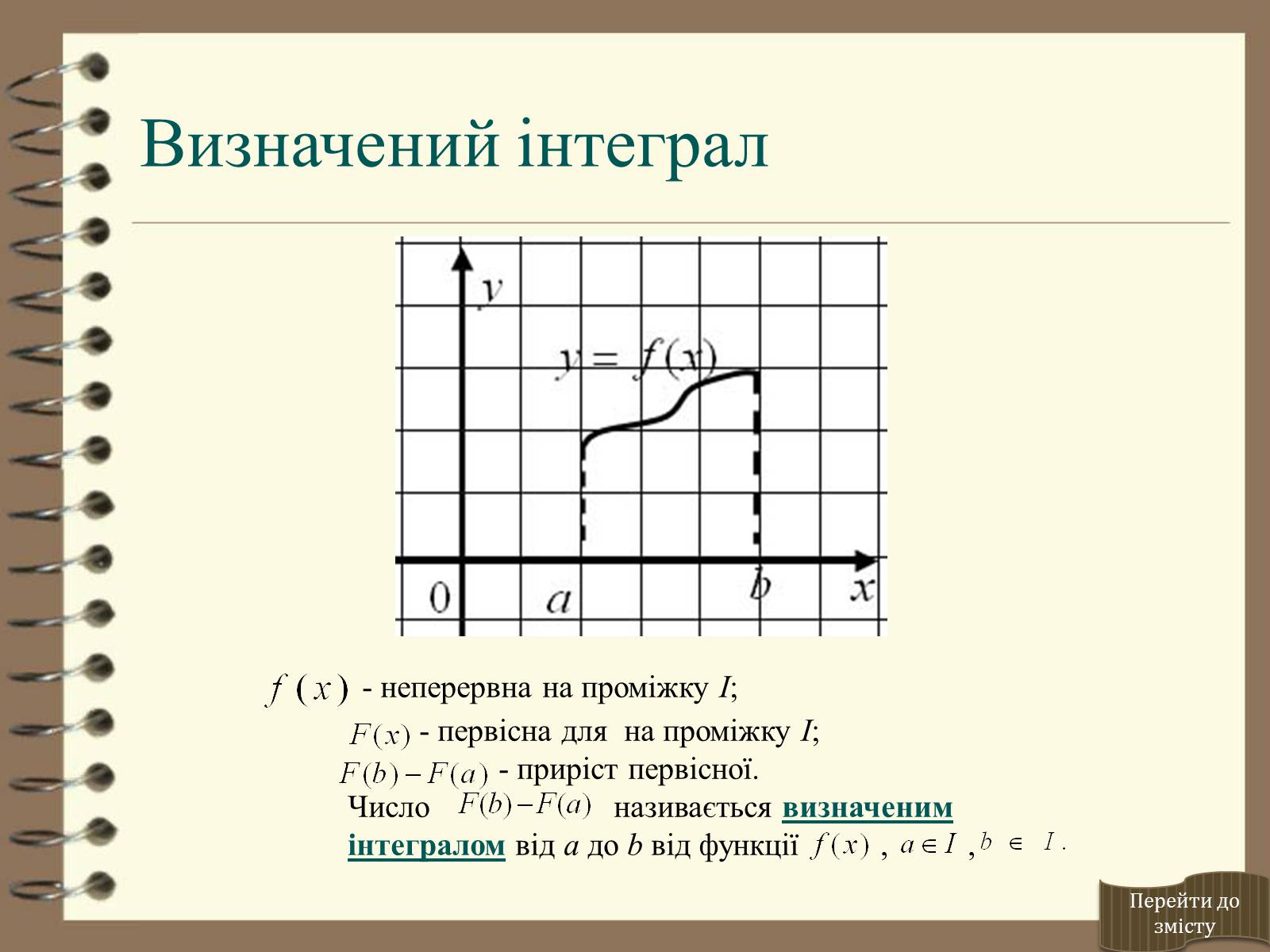
Визначений інтеграл
- неперервна на проміжку І;
- первісна для на проміжку І;
- приріст первісної.
Числоназивається визначеним інтегралом від a до b від функції , ,
Перейти до змісту
- неперервна на проміжку І;
- первісна для на проміжку І;
- приріст первісної.
Числоназивається визначеним інтегралом від a до b від функції , ,
Перейти до змісту
Слайд #14
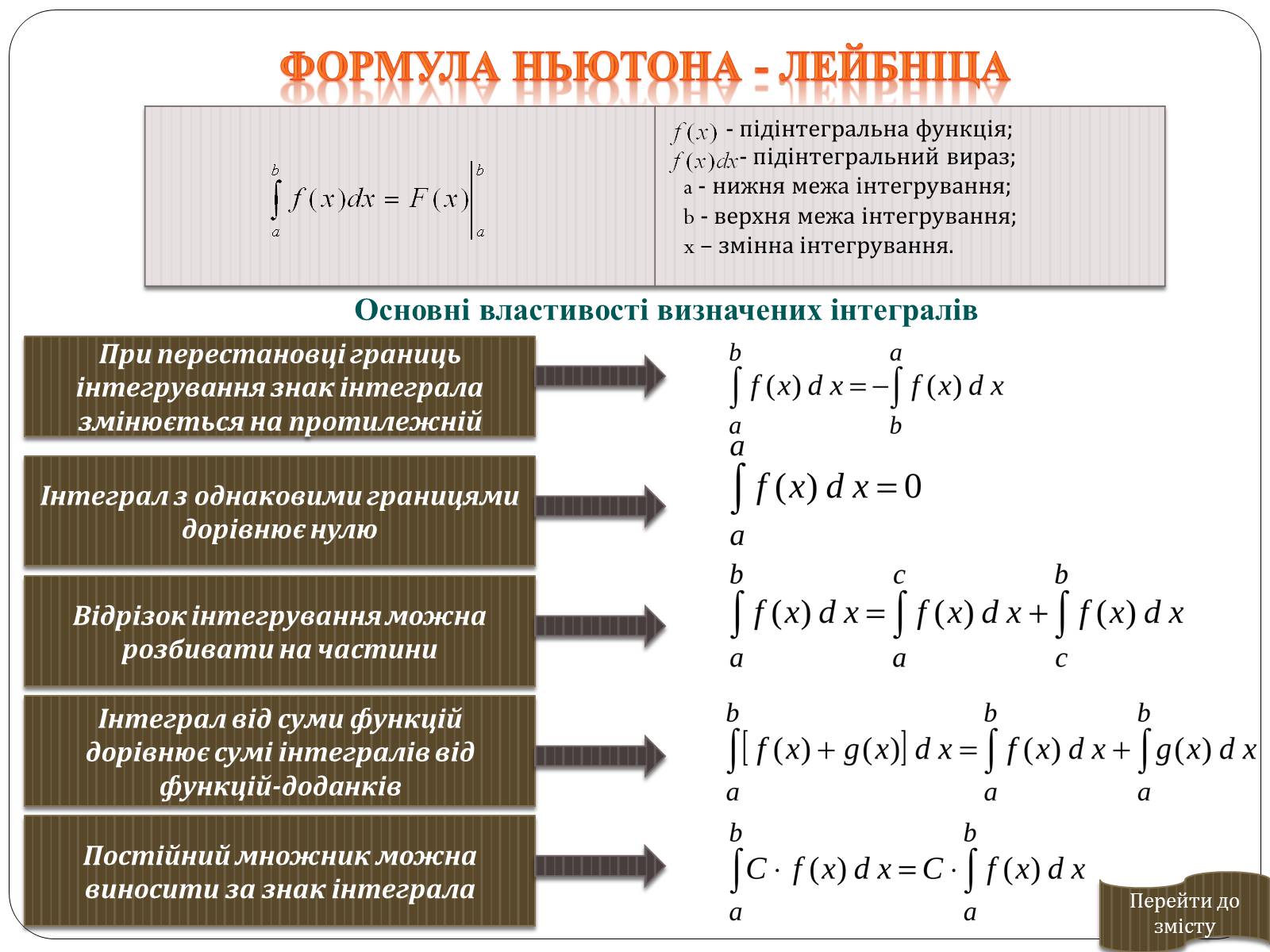
Формула Ньютона - Лейбніца
- підінтегральна функція;
- підінтегральний вираз;
a - нижня межа інтегрування;
b - верхня межа інтегрування;
x – змінна інтегрування.
Основні властивості визначених інтегралів
При перестановці границь інтегрування знак інтеграла змінюється на протилежній
Інтеграл з однаковими границями дорівнює нулю
Відрізок інтегрування можна розбивати на частини
Інтеграл від суми функцій дорівнює сумі інтегралів від функцій-доданків
Постійний множник можна виносити за знак інтеграла
Перейти до змісту
- підінтегральна функція;
- підінтегральний вираз;
a - нижня межа інтегрування;
b - верхня межа інтегрування;
x – змінна інтегрування.
Основні властивості визначених інтегралів
При перестановці границь інтегрування знак інтеграла змінюється на протилежній
Інтеграл з однаковими границями дорівнює нулю
Відрізок інтегрування можна розбивати на частини
Інтеграл від суми функцій дорівнює сумі інтегралів від функцій-доданків
Постійний множник можна виносити за знак інтеграла
Перейти до змісту
Слайд #15
1. 1.
А Б В А Б В
2. 2.
А Б В А Б В
3. 3.
А Б В А Б В
ВАРІАНТ І
ВАРІАНТ ІІ
Тестові завдання
Перейти до змісту
А Б В А Б В
2. 2.
А Б В А Б В
3. 3.
А Б В А Б В
ВАРІАНТ І
ВАРІАНТ ІІ
Тестові завдання
Перейти до змісту

Слайд #16
4. 4.
А Б В А Б В
5. 5.
А Б В А Б В
ВАРІАНТ І
ВАРІАНТ ІІ
Тестові завдання
Відповіді
Перейти до змісту
А Б В А Б В
5. 5.
А Б В А Б В
ВАРІАНТ І
ВАРІАНТ ІІ
Тестові завдання
Відповіді
Перейти до змісту

Слайд #17
Завдання
1. Знайти загальний вигляд первісної для функції:
2. Для функції знайти первісну, графік
якої проходить через точку А:
А(-1;-3);
А(1;2);
Відповіді
А
А
Б
Б
А
А
ВАРІАНТ І
ВАРІАНТ ІІ
Перейти до змісту
1. Знайти загальний вигляд первісної для функції:
2. Для функції знайти первісну, графік
якої проходить через точку А:
А(-1;-3);
А(1;2);
Відповіді
А
А
Б
Б
А
А
ВАРІАНТ І
ВАРІАНТ ІІ
Перейти до змісту

Слайд #18
3. Обчислити інтеграл:
Відповіді
А
А
Б
Б
ВАРІАНТ ІІ
ВАРІАНТ І
Перейти до змісту
Відповіді
А
А
Б
Б
ВАРІАНТ ІІ
ВАРІАНТ І
Перейти до змісту

Слайд #19
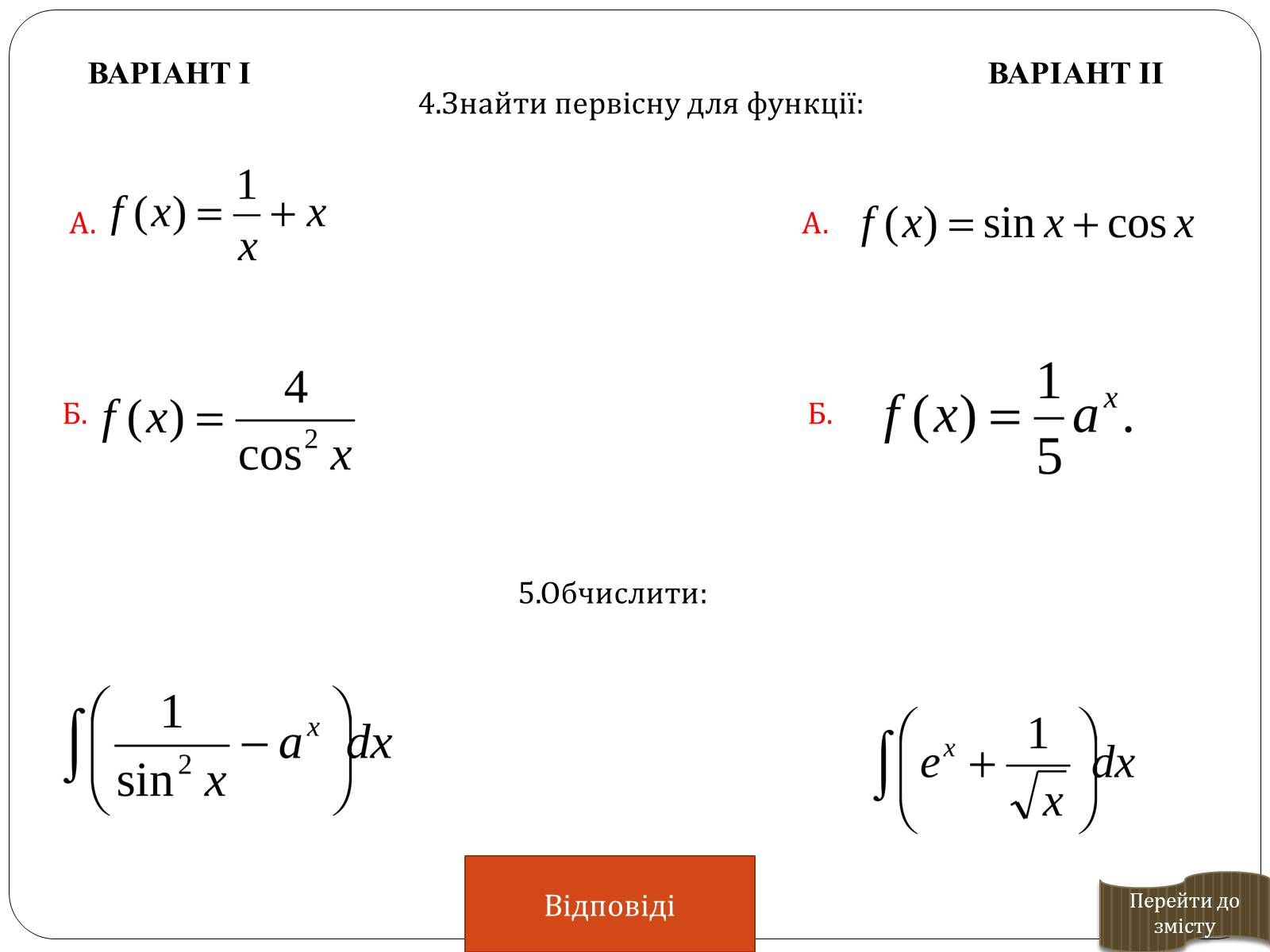
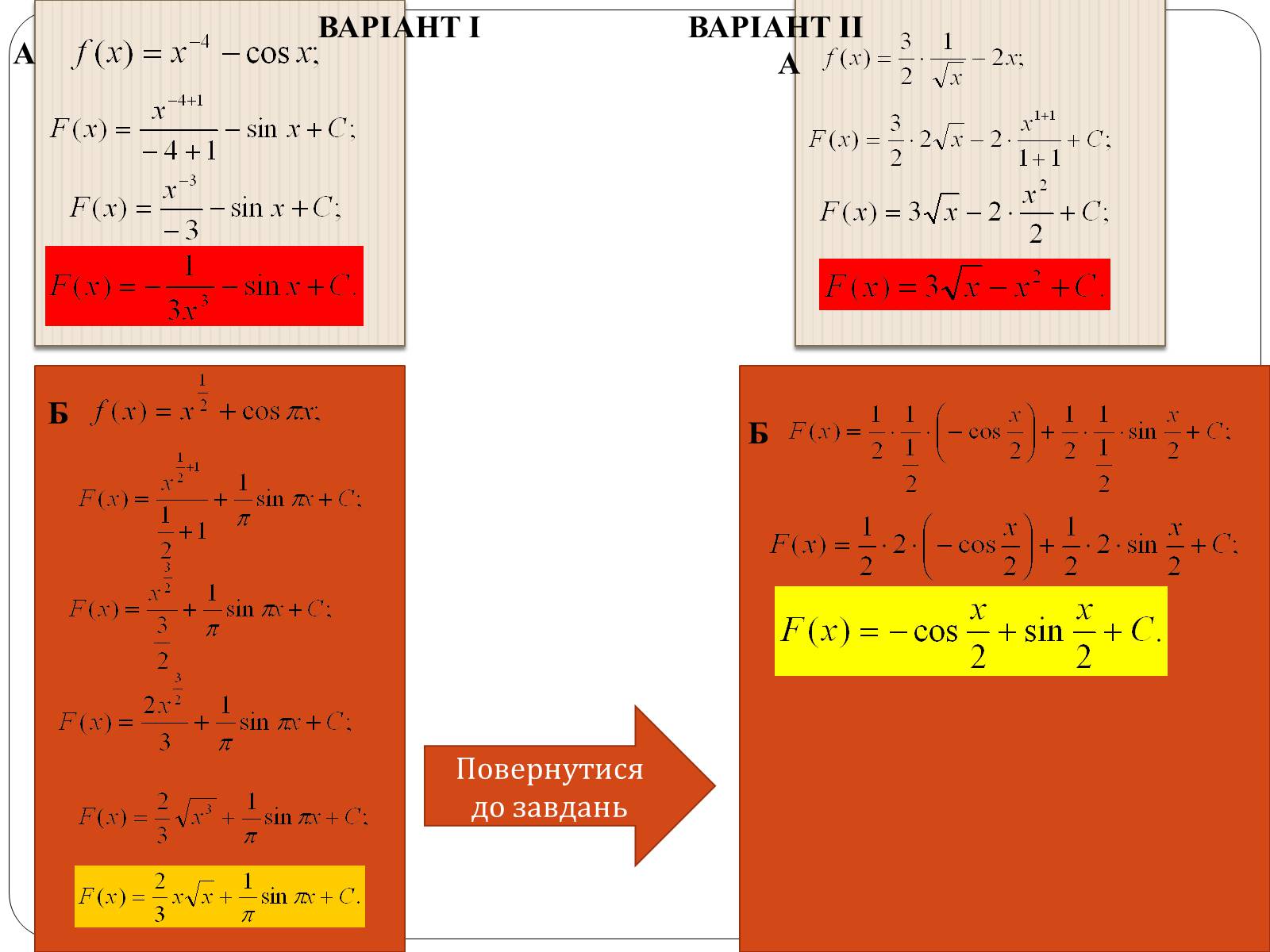
4.Знайти первісну для функції:
ВАРІАНТ ІІ
ВАРІАНТ І
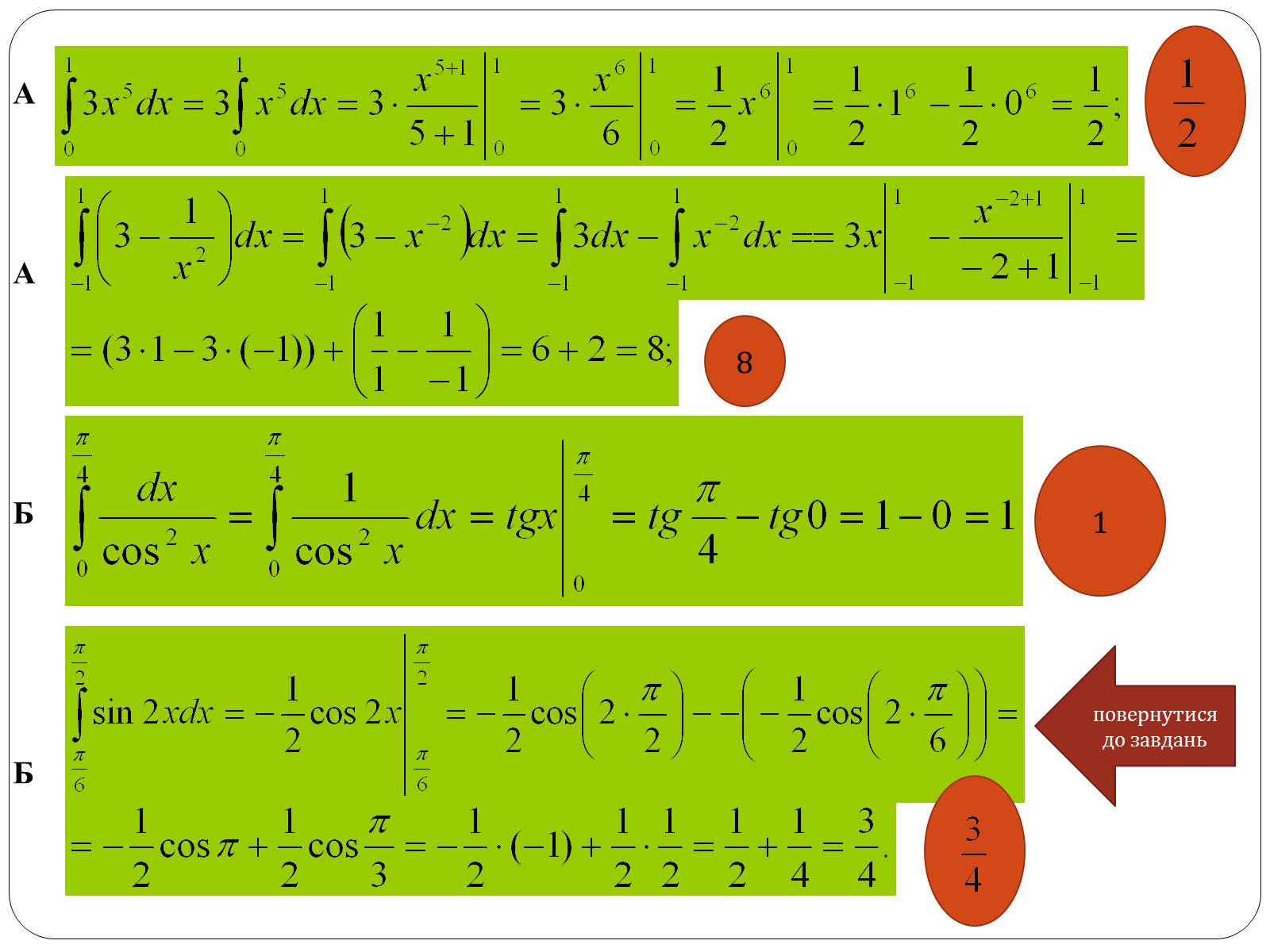
5.Обчислити:
А. А.
Б. Б.
Відповіді
Перейти до змісту
ВАРІАНТ ІІ
ВАРІАНТ І
5.Обчислити:
А. А.
Б. Б.
Відповіді
Перейти до змісту
Слайд #20
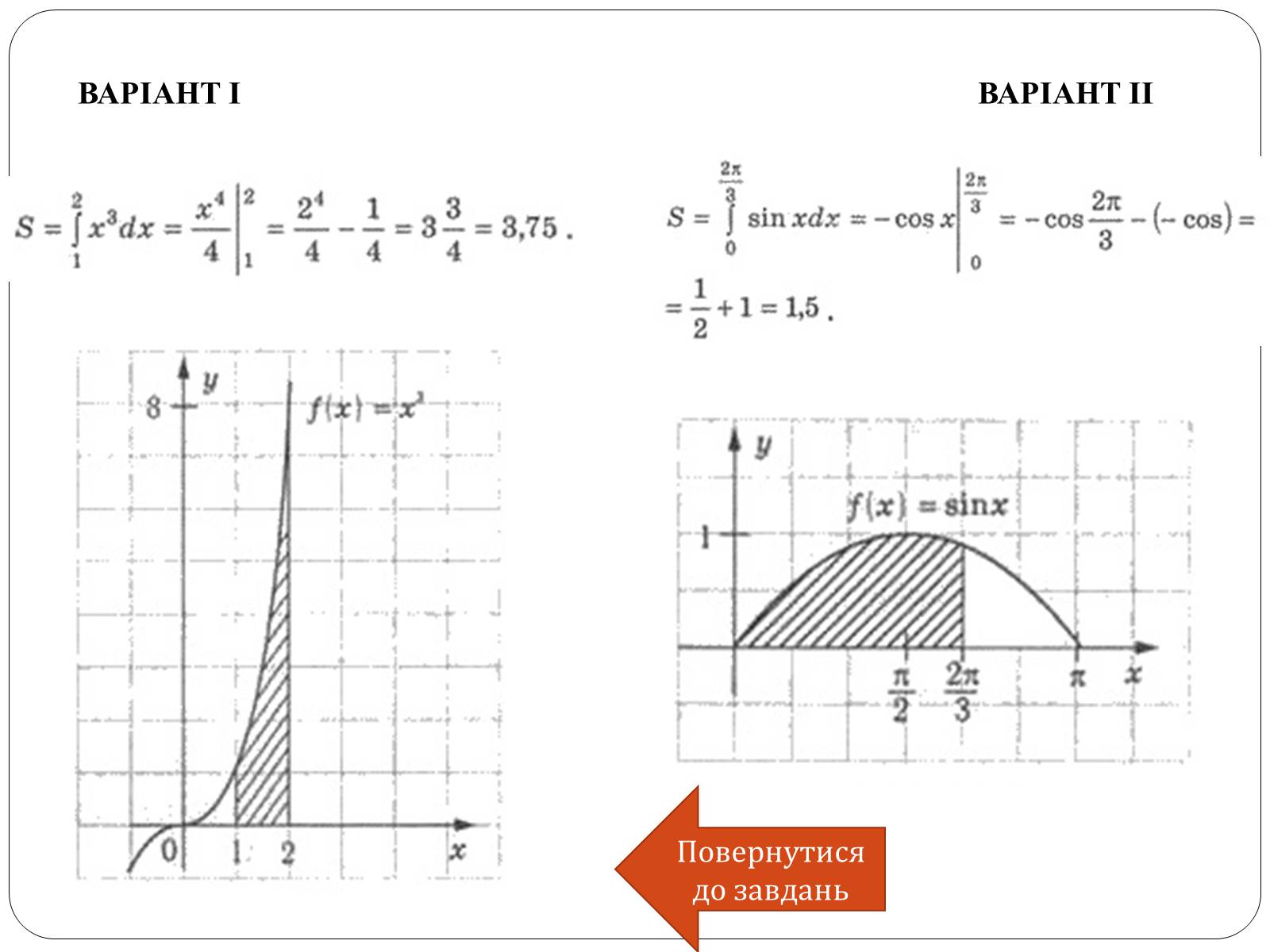
6.Обчисліть площу криволінійної трапеції, обчисленої графіком функції f(х) = х3 та прямими у = 0; х = 1; х = 2.
ВАРІАНТ ІІ
ВАРІАНТ І
6.Обчисліть площу криволінійної трапеції обмеженої графіком функції f(x) = sin х та прямими
Відповіді
Перейти до змісту
ВАРІАНТ ІІ
ВАРІАНТ І
6.Обчисліть площу криволінійної трапеції обмеженої графіком функції f(x) = sin х та прямими
Відповіді
Перейти до змісту

Слайд #21
Дякую за увагу!
Перейти до змісту
Перейти до змісту

Слайд #22
ВАРІАНТ І
ВАРІАНТ ІІ
А
А
Б
Б
Повернутися до завдань
ВАРІАНТ ІІ
А
А
Б
Б
Повернутися до завдань
Слайд #23
А(-1;3);
С=-6
А(1;2);
С=4
повернутися до завдань
ВАРІАНТ І
ВАРІАНТ ІІ
А
А
С=-6
А(1;2);
С=4
повернутися до завдань
ВАРІАНТ І
ВАРІАНТ ІІ
А
А

Слайд #24
8
1
повернутися до завдань
А
А
Б
Б
1
повернутися до завдань
А
А
Б
Б
Слайд #25
ВАРІАНТ ІІ
ВАРІАНТ І
Повернутися до завдань
ВАРІАНТ І
Повернутися до завдань
Слайд #26
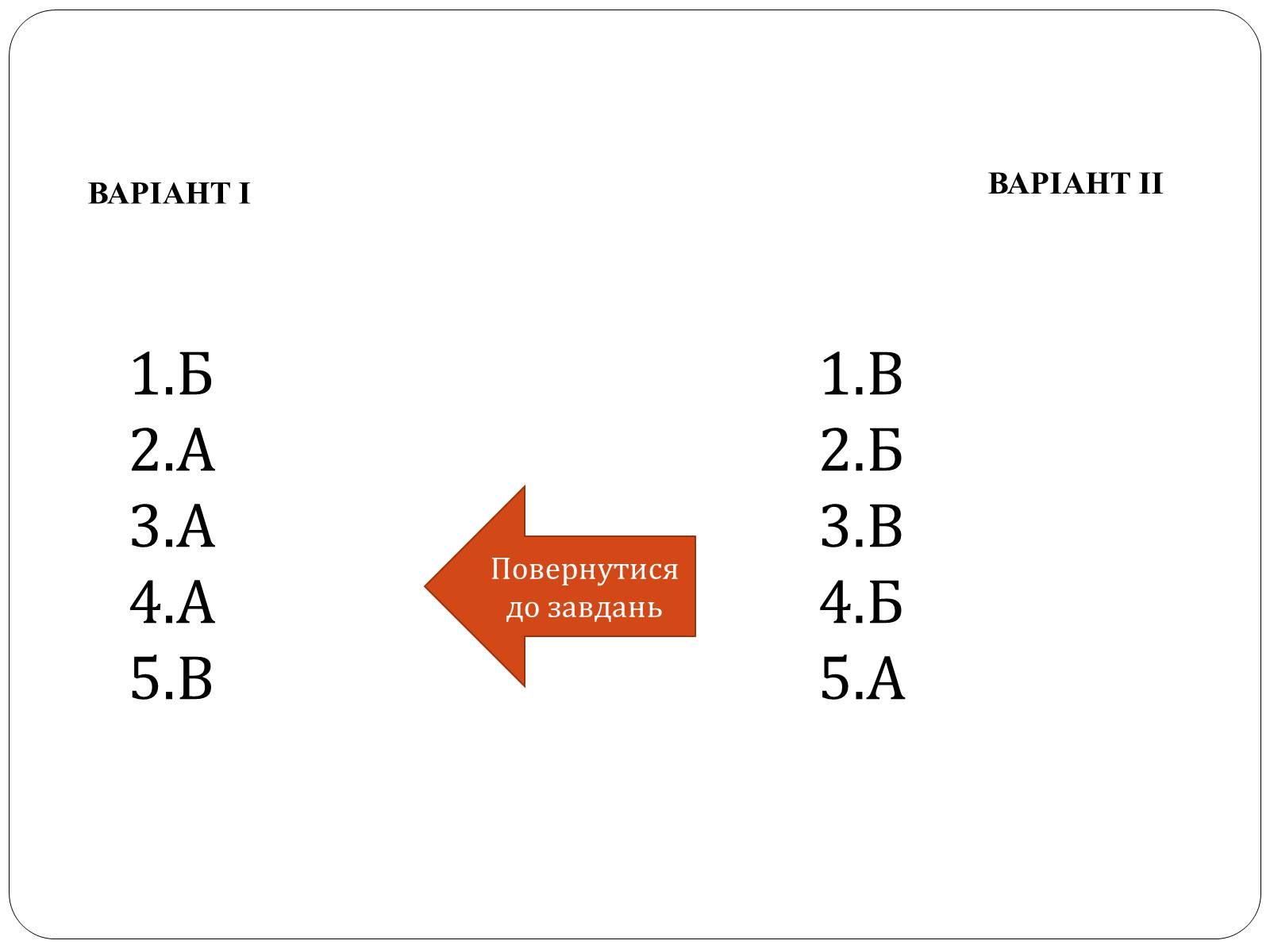
ВАРІАНТ І
ВАРІАНТ ІІ
Б
А
А
А
В
В
Б
В
Б
А
Повернутися до завдань
ВАРІАНТ ІІ
Б
А
А
А
В
В
Б
В
Б
А
Повернутися до завдань
Слайд #27
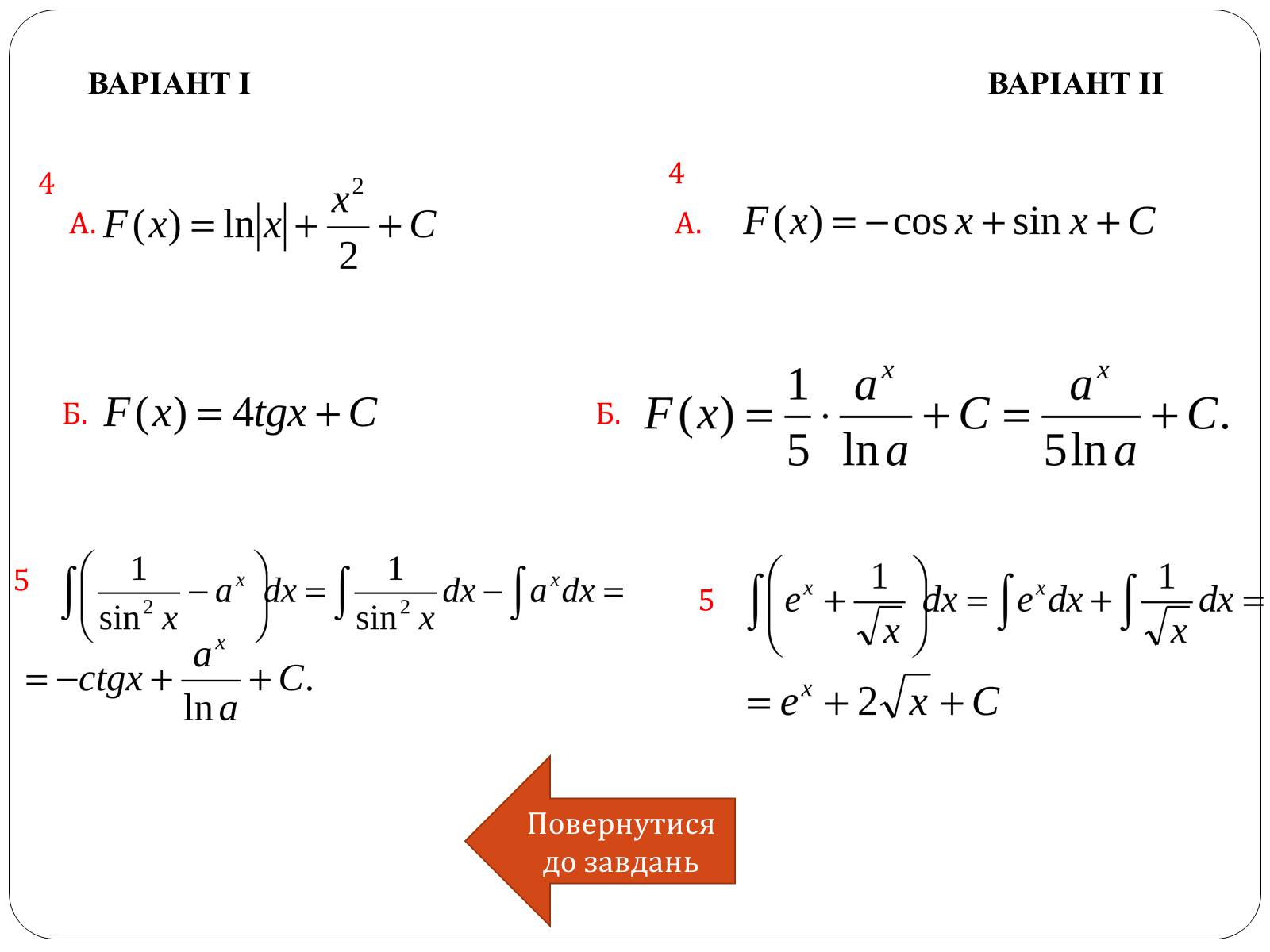
А. А.
Б. Б.
ВАРІАНТ І
ВАРІАНТ ІІ
4
4
5
5
Повернутися до завдань
Б. Б.
ВАРІАНТ І
ВАРІАНТ ІІ
4
4
5
5
Повернутися до завдань
Слайд #28
А. А.
Б. Б.
ВАРІАНТ І
ВАРІАНТ ІІ
4
4
5
5
Повернутися до завдань
Б. Б.
ВАРІАНТ І
ВАРІАНТ ІІ
4
4
5
5
Повернутися до завдань
Слайд #29
А. А.
Б. Б.
ВАРІАНТ І
ВАРІАНТ ІІ
4
4
5
5
Повернутися до завдань
Б. Б.
ВАРІАНТ І
ВАРІАНТ ІІ
4
4
5
5
Повернутися до завдань
Слайд #30
Не вірно
Повернутися до завдань
Повернутися до завдань

Слайд #31
Правильна відповідь
Поернутися до завдань
Поернутися до завдань

Слайд #32
Правильна відповідь
Повернутися до завдань
Повернутися до завдань

Слайд #33
Не вірно
Повернутися до завдань
Повернутися до завдань
