- Головна
- Готові шкільні презентації
- Презентація на тему «Вектори» (варіант 2)
Презентація на тему «Вектори» (варіант 2)
300
Слайд #1
Геометрія 9 клас
Презентація на тему :
Вектори
Презентація на тему :
Вектори

Слайд #2
Означення вектора
Означення довжини вектора
Означення нульового вектора
Означення колінеарних векторів
Означення співнапрямлених та протилежно напрямлених векторів
Рівні вектори
Задачі
Означення довжини вектора
Означення нульового вектора
Означення колінеарних векторів
Означення співнапрямлених та протилежно напрямлених векторів
Рівні вектори
Задачі

Слайд #3
Історична довідка
Інтерес до векторів виник у математиків у ХІХ ст. у зв'язку з потребами фізики й механіки. Але витоки числення з напрямленими відрізками знаходимо ще в далекій давнині, в роботах піфагорійців і геометричній теорій відношень Евдокса. У геометричному численні, що його виклав Евклід. Додавання і віднімання чисел заводилося до відповідних операцій з відрізками, а множення – до побудови прямокутника зі сторонами, довжини яких дорівнюють множникам. Подальший розвиток векторного методу пов'язаний зі становленням аналітичної геометрії і теорії геометричних перетворень. Вектор задано початковою точкою А та її образом В. Згодом відповідний розділ отримав назву «векторна алгебра».
Інтерес до векторів виник у математиків у ХІХ ст. у зв'язку з потребами фізики й механіки. Але витоки числення з напрямленими відрізками знаходимо ще в далекій давнині, в роботах піфагорійців і геометричній теорій відношень Евдокса. У геометричному численні, що його виклав Евклід. Додавання і віднімання чисел заводилося до відповідних операцій з відрізками, а множення – до побудови прямокутника зі сторонами, довжини яких дорівнюють множникам. Подальший розвиток векторного методу пов'язаний зі становленням аналітичної геометрії і теорії геометричних перетворень. Вектор задано початковою точкою А та її образом В. Згодом відповідний розділ отримав назву «векторна алгебра».

Слайд #4
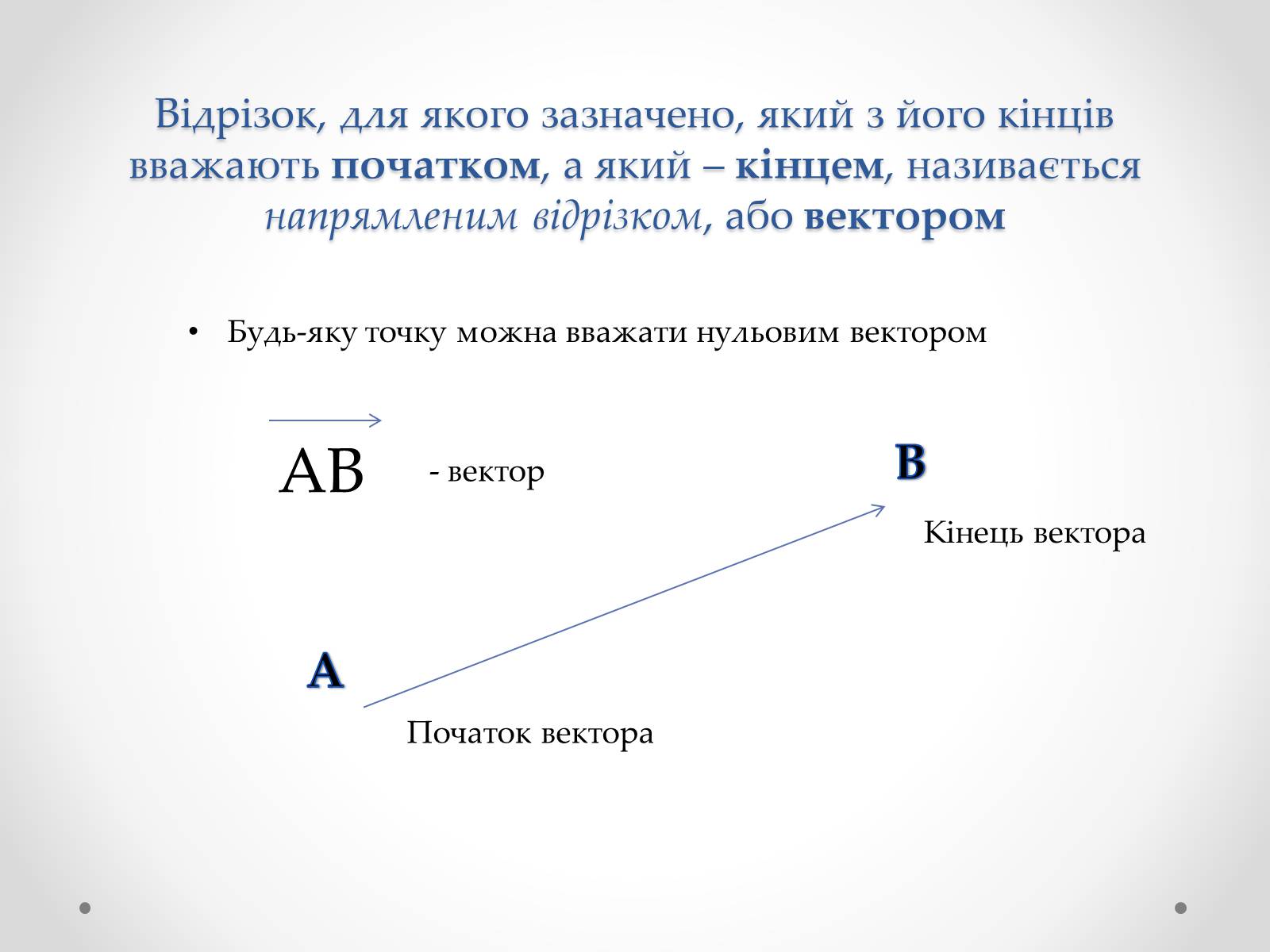
Відрізок, для якого зазначено, який з його кінців вважають початком, а який – кінцем, називається напрямленим відрізком, або вектором
А
В
Початок вектора
Кінець вектора
АВ
- вектор
Будь-яку точку можна вважати нульовим вектором
А
В
Початок вектора
Кінець вектора
АВ
- вектор
Будь-яку точку можна вважати нульовим вектором
Слайд #5
Означення довжини вектора
Модуль вектора (абсолютна величина вектора) – довжина відрізка, що зображує вектор.
Довжина вектора позначається так:
M
N
a
|MN| = |a| довжина векторa MN
Модуль вектора (абсолютна величина вектора) – довжина відрізка, що зображує вектор.
Довжина вектора позначається так:
M
N
a
|MN| = |a| довжина векторa MN

Слайд #6
Означення нульового вектора
Будь-яка точка площини є вектором. Такий вектор називається нульовим. Початок нульового вектора збігається з його кінцем. Довжина нульового вектора дорівнює нулю : = 0
К
вектор КК є нульовий вектор
|KK| = 0
Будь-яка точка площини є вектором. Такий вектор називається нульовим. Початок нульового вектора збігається з його кінцем. Довжина нульового вектора дорівнює нулю : = 0
К
вектор КК є нульовий вектор
|KK| = 0

Слайд #7
Означення колінеарних векторів
Ненульові вектори називаються колінеарними, якщо вони лежать на одній прямій, або на паралельних прямих; нульовий вектор вважають колінеарним будь-якому вектору.
А
В
F
E
C
D
Ненульові вектори називаються колінеарними, якщо вони лежать на одній прямій, або на паралельних прямих; нульовий вектор вважають колінеарним будь-якому вектору.
А
В
F
E
C
D

Слайд #8
Означення співнапрямлених векторів
Два ненульові вектори α і β називаються співнапрямленими або однаково напрямленими
α ↑↑ β ,якщо вони колінеарні і лежать в одній півплощині відносно прямої, яка сполучає їх початки.
α
β
α ↑↑ β
Два ненульові вектори α і β називаються співнапрямленими або однаково напрямленими
α ↑↑ β ,якщо вони колінеарні і лежать в одній півплощині відносно прямої, яка сполучає їх початки.
α
β
α ↑↑ β

Слайд #9
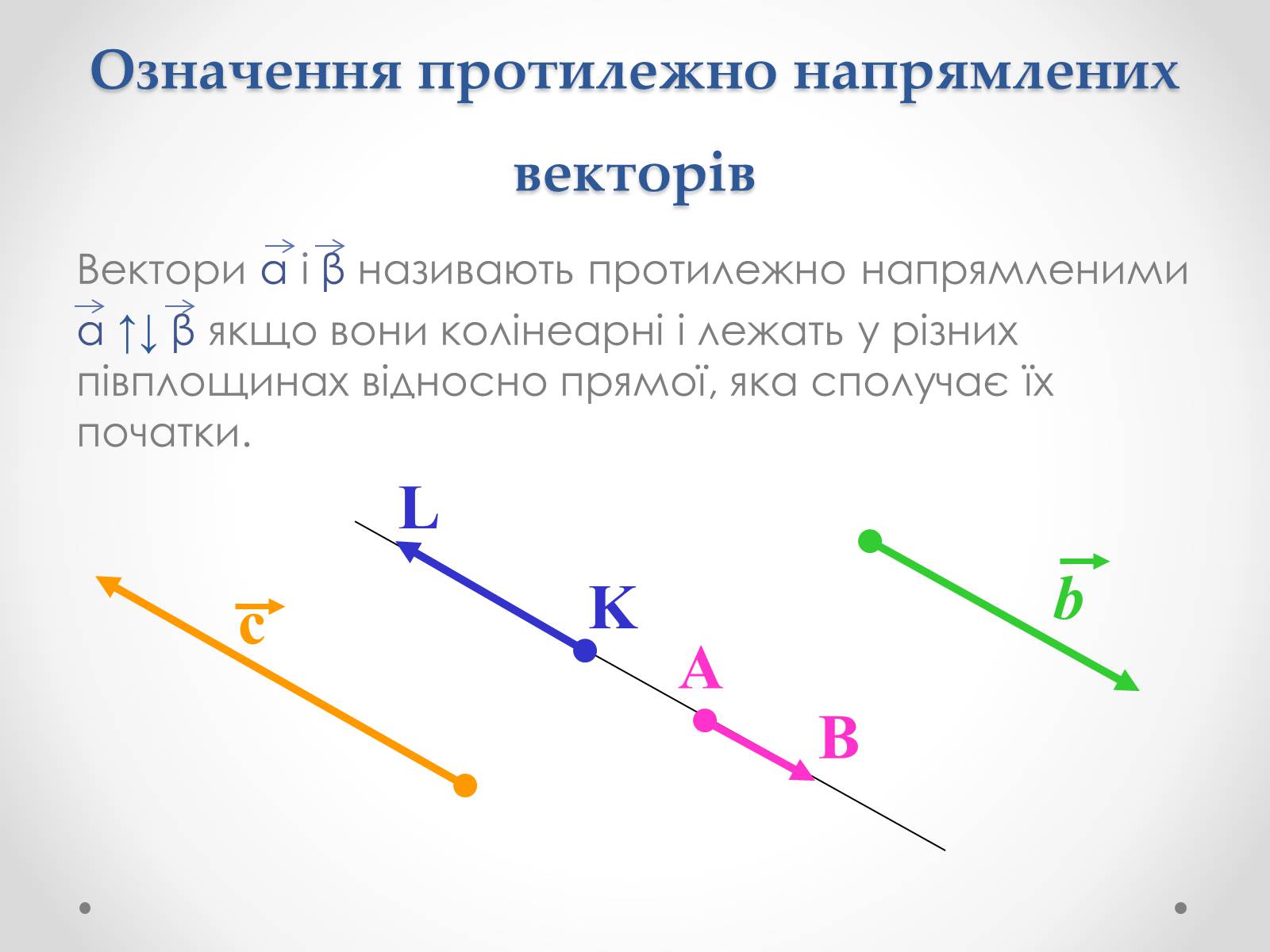
Означення протилежно напрямлених векторів
Вектори α і β називають протилежно напрямленими
α ↑↓ β якщо вони колінеарні і лежать у різних півплощинах відносно прямої, яка сполучає їх початки.
с
L
K
A
B
b
Вектори α і β називають протилежно напрямленими
α ↑↓ β якщо вони колінеарні і лежать у різних півплощинах відносно прямої, яка сполучає їх початки.
с
L
K
A
B
b
Слайд #10
Означення про рівні вектори
Вектори називаються рівними, якщо вони співнапрямлені і їх довжини рівні.
Якщо деяка точка – початок вектора,то кажуть, що цей вектор відкладено від даної точки.
Від будь-якої точки можна відкласти вектор,що дорівнює даному і до того ж тільки один.
Зауваження : Рівні вектори, відкладені від різних точок, часто позначають однією і тією ж буквою ; інколи кажуть, що це один і той же вектор, але відкладений від різних точок.
Вектори називаються рівними, якщо вони співнапрямлені і їх довжини рівні.
Якщо деяка точка – початок вектора,то кажуть, що цей вектор відкладено від даної точки.
Від будь-якої точки можна відкласти вектор,що дорівнює даному і до того ж тільки один.
Зауваження : Рівні вектори, відкладені від різних точок, часто позначають однією і тією ж буквою ; інколи кажуть, що це один і той же вектор, але відкладений від різних точок.

Слайд #11
Завдання 1
Які з векторів, зображених на рисунку :
1)рівні ; 2)співнапрямлені ; 3)протилежно напрямлені ; 4)колінеарні ; 5)мають рівні модулі ?
Які з векторів, зображених на рисунку :
1)рівні ; 2)співнапрямлені ; 3)протилежно напрямлені ; 4)колінеарні ; 5)мають рівні модулі ?

Слайд #12
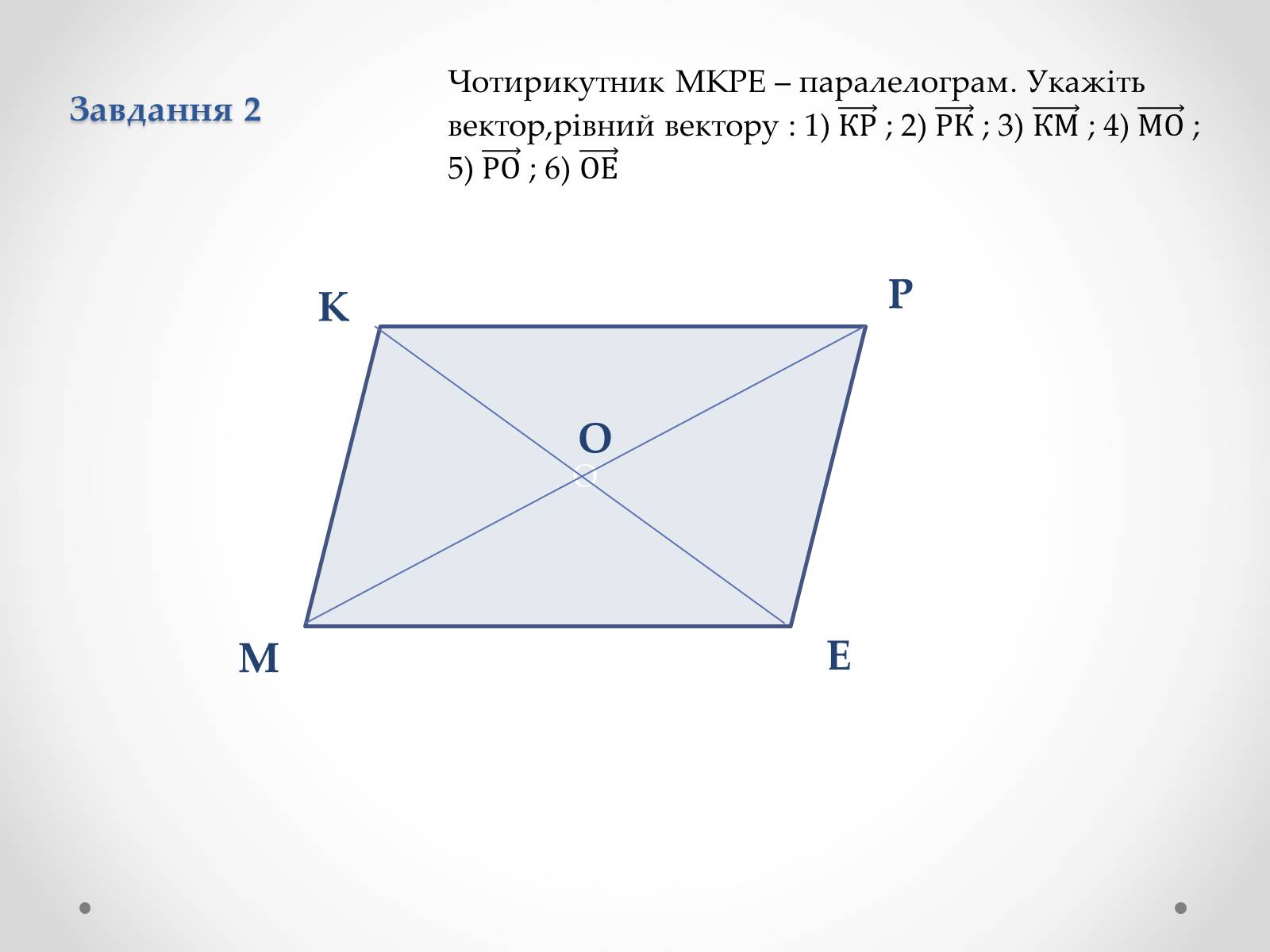
Завдання 2
Чотирикутник МКРЕ – паралелограм. Укажіть вектор,рівний вектору : 1) ; 2) ; 3) ; 4) ;
5) ; 6)
О
М
К
Р
Е
О
Чотирикутник МКРЕ – паралелограм. Укажіть вектор,рівний вектору : 1) ; 2) ; 3) ; 4) ;
5) ; 6)
О
М
К
Р
Е
О