- Головна
- Готові шкільні презентації
- Презентація на тему «Многогранники» (варіант 4)
Презентація на тему «Многогранники» (варіант 4)
294
Слайд #1
Многогранники

Слайд #2
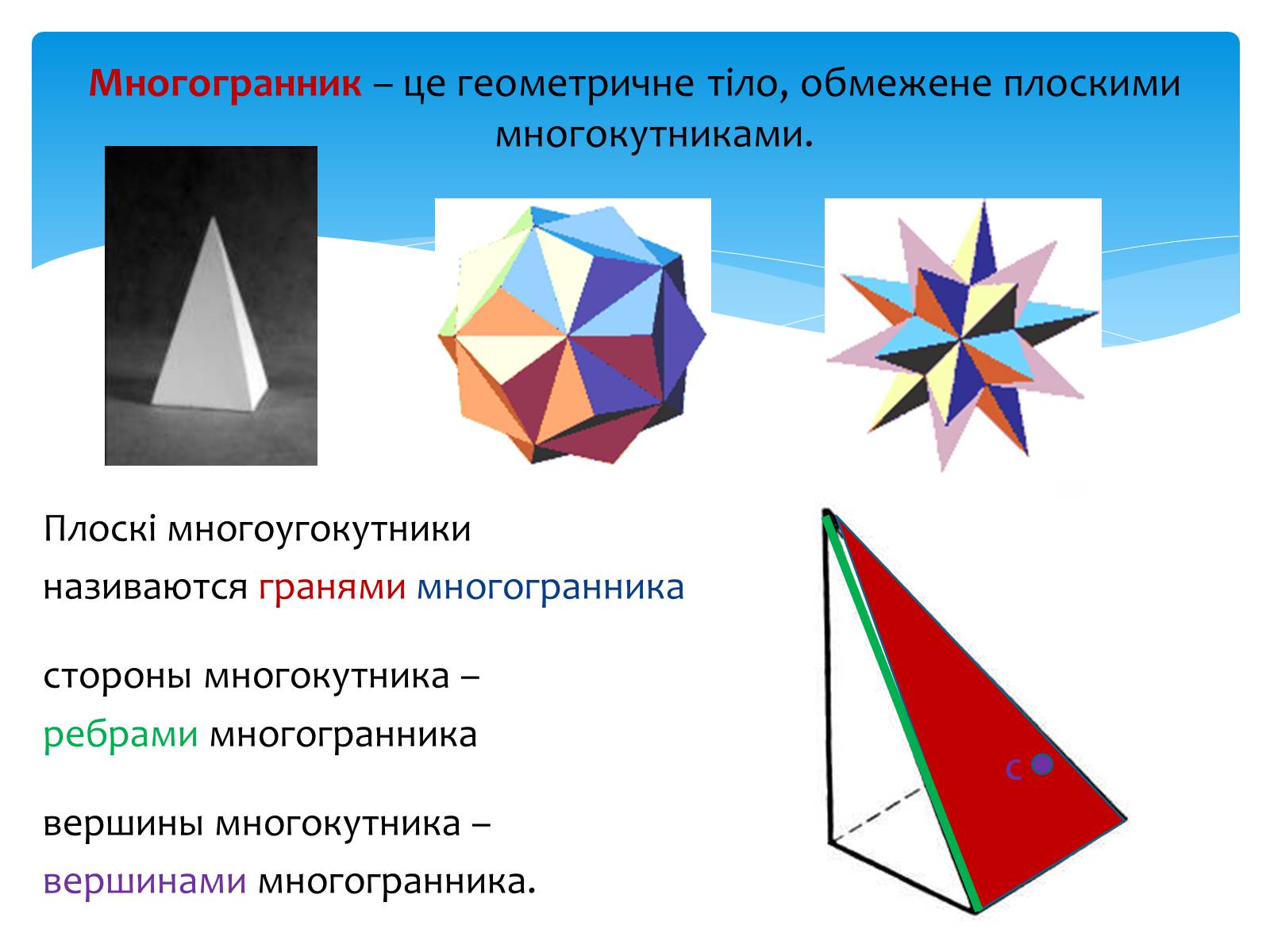
Многогранник – це геометричне тіло, обмежене плоскими многокутниками.
Плоскі многоугокутники
називаются гранями многогранника
стороны многокутника –
ребрами многогранника
вершины многокутника –
вершинами многогранника.
С
Плоскі многоугокутники
називаются гранями многогранника
стороны многокутника –
ребрами многогранника
вершины многокутника –
вершинами многогранника.
С
Слайд #3
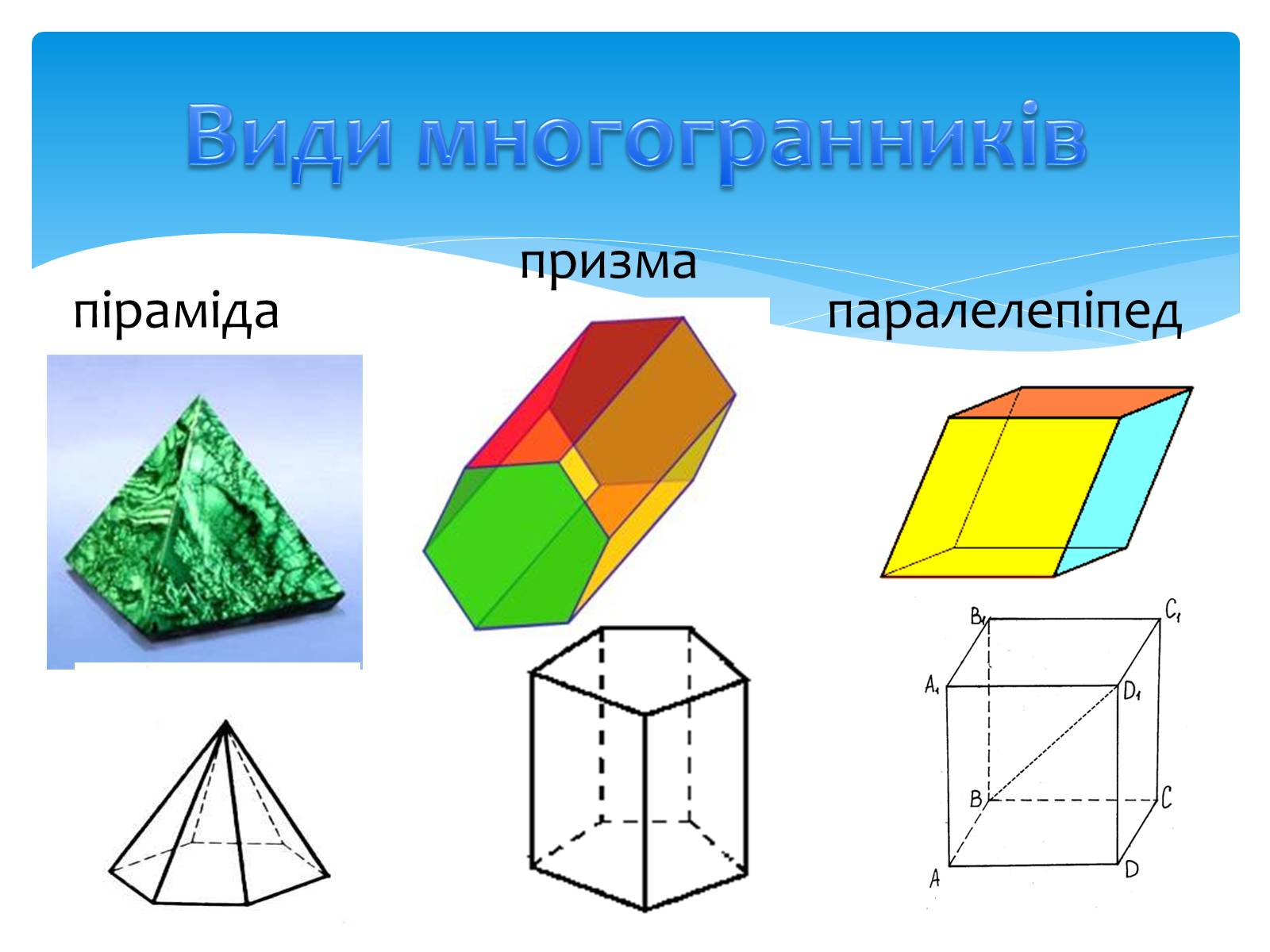
піраміда
призма
паралелепіпед
Види многогранників
призма
паралелепіпед
Види многогранників
Слайд #4
Піраміда называется правильною,
якщо в основі лежить правильный многокутник, а вершина проектується
в центр основи
Піраміда - це многогранник
Основою піраміди є многокутник
бічні грані -- трикутники
(n-кутна пірамида має n+1 граней)
якщо в основі лежить правильный многокутник, а вершина проектується
в центр основи
Піраміда - це многогранник
Основою піраміди є многокутник
бічні грані -- трикутники
(n-кутна пірамида має n+1 граней)

Слайд #5
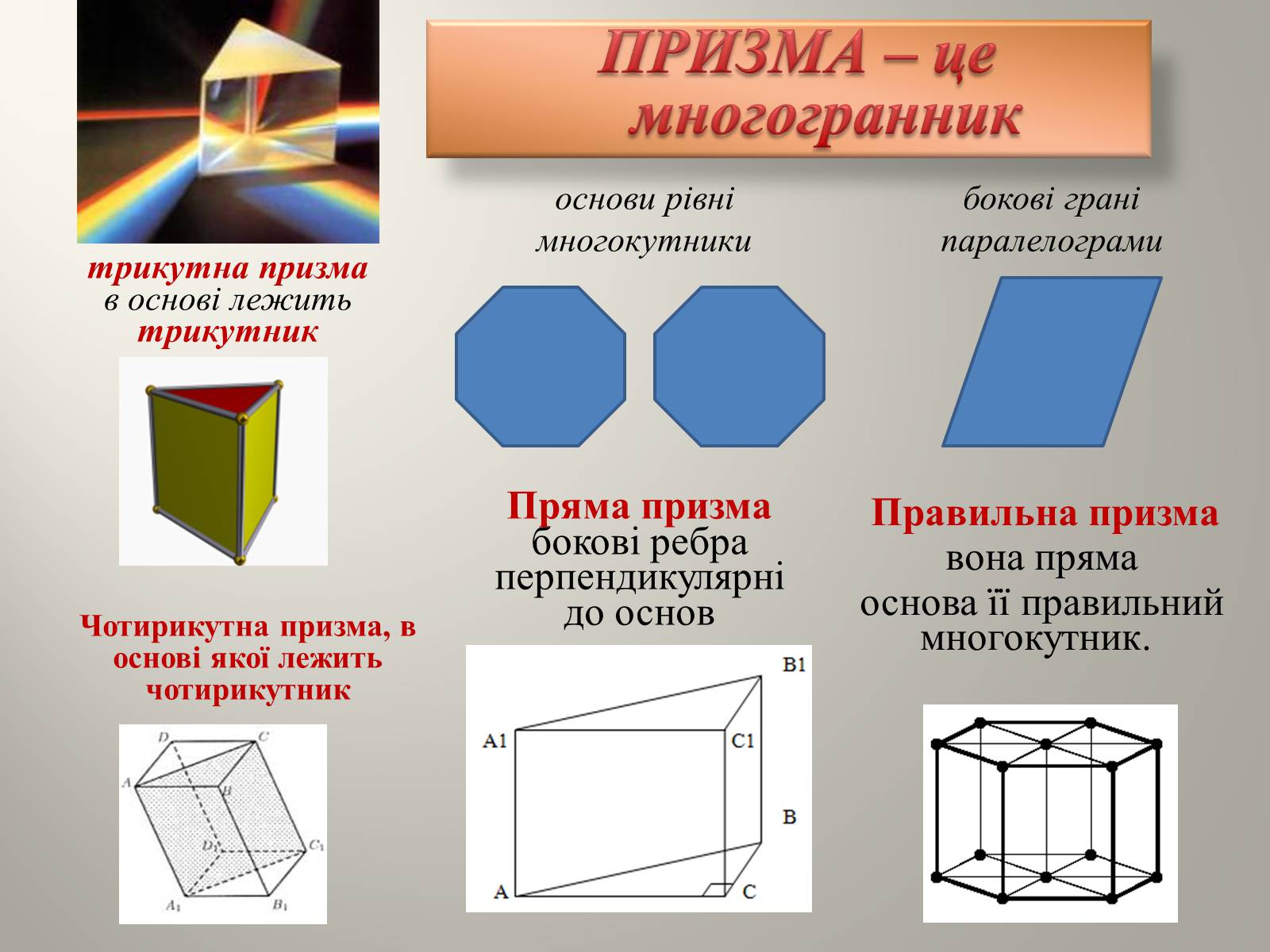
Правильна призма
вона пряма
основа її правильний многокутник.
ПРИЗМА – це многогранник
основи рівні многокутники
бокові грані паралелограми
Чотирикутна призма, в основі якої лежить чотирикутник
трикутна призма
в основі лежить трикутник
Пряма призма бокові ребра перпендикулярні до основ
вона пряма
основа її правильний многокутник.
ПРИЗМА – це многогранник
основи рівні многокутники
бокові грані паралелограми
Чотирикутна призма, в основі якої лежить чотирикутник
трикутна призма
в основі лежить трикутник
Пряма призма бокові ребра перпендикулярні до основ
Слайд #6
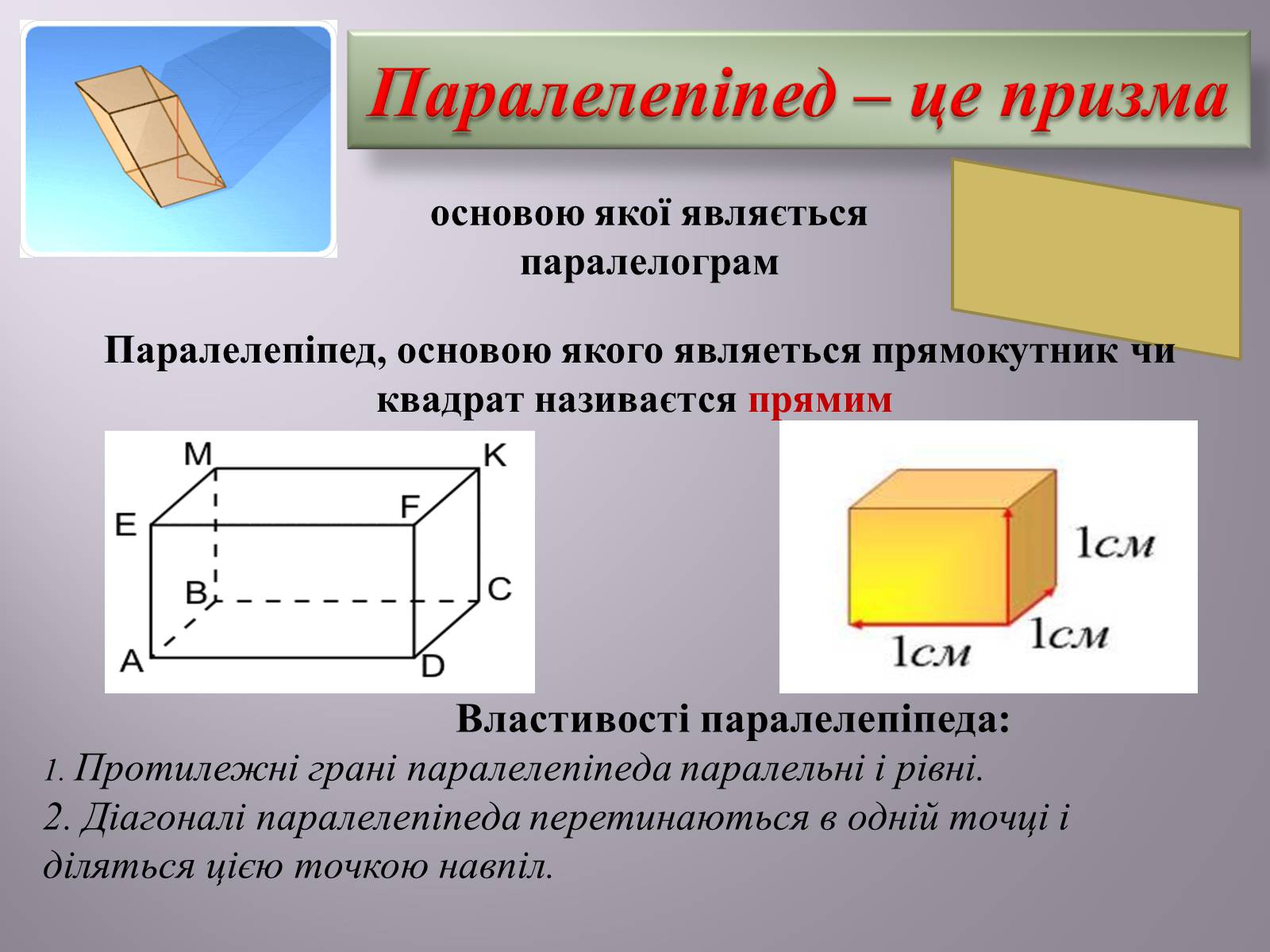
Паралелепіпед – це призма
основою якої являється паралелограм
Паралелепіпед, основою якого являеться прямокутник чи квадрат називаєтся прямим
Властивості паралелепіпеда:1. Протилежні грані паралелепіпеда паралельні і рівні.2. Діагоналі паралелепіпеда перетинаються в одній точці і діляться цією точкою навпіл.
основою якої являється паралелограм
Паралелепіпед, основою якого являеться прямокутник чи квадрат називаєтся прямим
Властивості паралелепіпеда:1. Протилежні грані паралелепіпеда паралельні і рівні.2. Діагоналі паралелепіпеда перетинаються в одній точці і діляться цією точкою навпіл.
Слайд #7
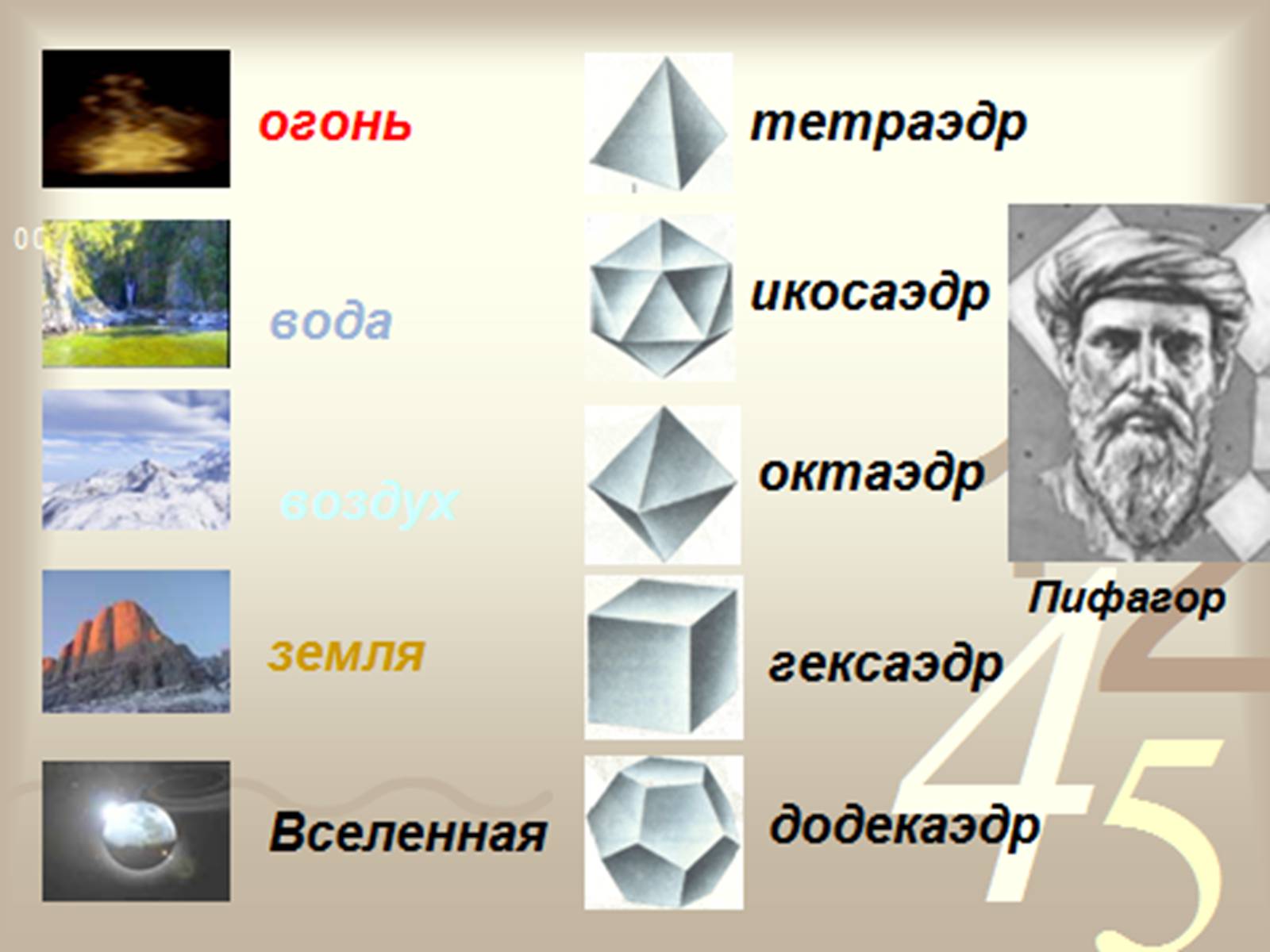
Правильні многогранники
Тетраэдр
Куб
Октаэдр
Икосаэдр
Додекаэдр
Тетраэдр
Куб
Октаэдр
Икосаэдр
Додекаэдр

Слайд #8
Тетраедр
( від ,,тетра”- чотири і грецького ,,hedra” - грань)
складається з 4-х правильних трикутників, в кожній його вершині сходяться 3 ребра.
тетраедр-вогонь
Тетраедр символізував вогонь,
т.к. його вершина напрямлена вгору.
( від ,,тетра”- чотири і грецького ,,hedra” - грань)
складається з 4-х правильних трикутників, в кожній його вершині сходяться 3 ребра.
тетраедр-вогонь
Тетраедр символізував вогонь,
т.к. його вершина напрямлена вгору.

Слайд #9
Гексаедр (куб)
гексаедр (куб) - земля
Гексаедр (куб) символізував землю,
так як «найстійкіший»
(від грецького ,,гекса” - шість и ,,hedra” - грань) має 6 квадратних граней, в кажній його вершині сходятся 3 ребра.
Гексаедр більш відомий як куб (від латинського ,,cubus”; від грецького ,,kubos”.
гексаедр (куб) - земля
Гексаедр (куб) символізував землю,
так як «найстійкіший»
(від грецького ,,гекса” - шість и ,,hedra” - грань) має 6 квадратних граней, в кажній його вершині сходятся 3 ребра.
Гексаедр більш відомий як куб (від латинського ,,cubus”; від грецького ,,kubos”.

Слайд #10
Октаедр
октаедр-повітря
(від грецького okto - вісім и hedra - грань)
має 8 граней (трикутник),
в кажній вершині сходяться 4 ребра.
Октаэдр символізував повітря,
як "найповітряніший"
октаедр-повітря
(від грецького okto - вісім и hedra - грань)
має 8 граней (трикутник),
в кажній вершині сходяться 4 ребра.
Октаэдр символізував повітря,
як "найповітряніший"

Слайд #11
Ікосаедр
ікосаедр-вода
ікосаедр символизував воду,
так як він «обтічний»
(від грецького eikosi - двадцять и hedra - грань)
має 20 граней (трикутних),
в кожній вершині сходиться 5 ребер
ікосаедр-вода
ікосаедр символизував воду,
так як він «обтічний»
(від грецького eikosi - двадцять и hedra - грань)
має 20 граней (трикутних),
в кожній вершині сходиться 5 ребер

Слайд #12
Додекаедр
додекаедр-всесвіт!
Додекаедр втілював у собі "все суще", символізував все світотворення, вважався головним.
(від грецького dodeka - дванадцять и hedra - грань) має 12 граней (п'ятикутних),
в каждой вершине сходятся 3 ребра.
додекаедр-всесвіт!
Додекаедр втілював у собі "все суще", символізував все світотворення, вважався головним.
(від грецького dodeka - дванадцять и hedra - грань) має 12 граней (п'ятикутних),
в каждой вершине сходятся 3 ребра.

Слайд #13
Додекаедр
додекаедр-всесвіт!
Додекаедр втілював у собі "все суще", символізував все світотворення, вважався головним.
(від грецького dodeka - дванадцять и hedra - грань) має 12 граней (п'ятикутних),
в каждой вершине сходятся 3 ребра.
додекаедр-всесвіт!
Додекаедр втілював у собі "все суще", символізував все світотворення, вважався головним.
(від грецького dodeka - дванадцять и hedra - грань) має 12 граней (п'ятикутних),
в каждой вершине сходятся 3 ребра.
Слайд #14
Назви
Тетраедр
Куб
Октаедр
Додекаедр
Икосаедр
Форма граней
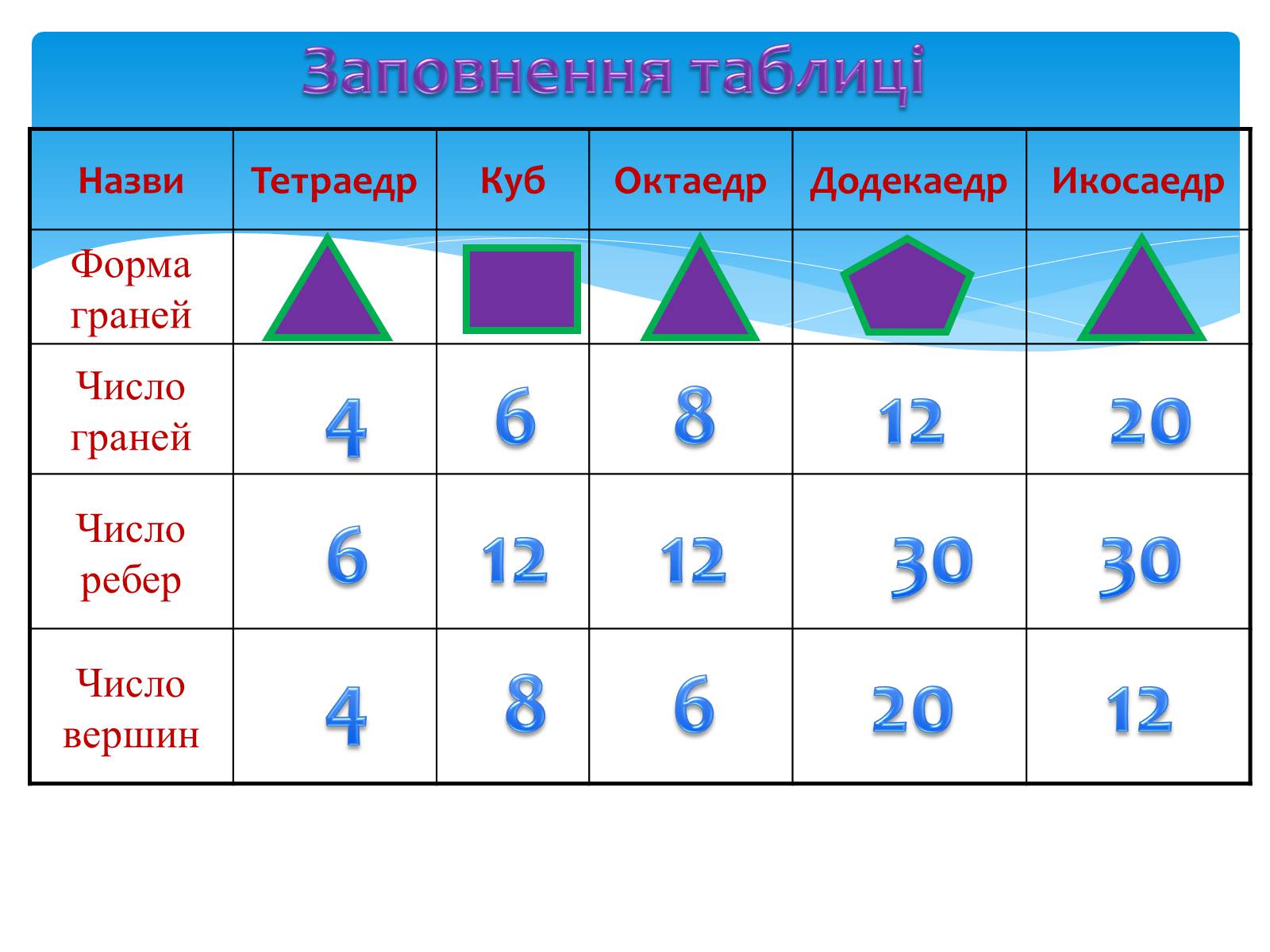
Число граней
Число ребер
Число вершин
Заповнення таблиці
4
4
6
6
6
8
8
12
12
12
12
20
20
30
30
Тетраедр
Куб
Октаедр
Додекаедр
Икосаедр
Форма граней
Число граней
Число ребер
Число вершин
Заповнення таблиці
4
4
6
6
6
8
8
12
12
12
12
20
20
30
30
Слайд #15
Теорема Ейлера:
Число вершин - число ребер + число граней =2
Швейцарський, німецкий і російский математик
автор більш ніж 800 робіт по математичному аналізу, диференційній геометрії, теорії музики та ін..
Леонард Эйлер
(1707-1783)
Число вершин, ребер та граней правильних многокутників повязане одне з одним цікавим співвідношенням.
Число вершин - число ребер + число граней =2
Швейцарський, німецкий і російский математик
автор більш ніж 800 робіт по математичному аналізу, диференційній геометрії, теорії музики та ін..
Леонард Эйлер
(1707-1783)
Число вершин, ребер та граней правильних многокутників повязане одне з одним цікавим співвідношенням.

Слайд #16
Математика - гімнастика для розуму, СТЕРЕОМЕТРіЯ - витамін для мозку.

Слайд #17
Велика піраміда в Гізі
Александрійский маяк
Нікольский собор
Галикарнаський мавзолей
Башня Сююмбике
Многогранники в архитектуре.
Мечеть
Кул-Шариф
Александрійский маяк
Нікольский собор
Галикарнаський мавзолей
Башня Сююмбике
Многогранники в архитектуре.
Мечеть
Кул-Шариф

Слайд #18
Многогранники в житті

Слайд #19
http://www.yandex.ru/
http://ru.wikipedia.org/
http://otherreferats.allbest.ru/mathematics/00050000_0.html
Библиография
http://ru.wikipedia.org/
http://otherreferats.allbest.ru/mathematics/00050000_0.html
Библиография
