Презентація на тему «Площа фігур»
263
Слайд #1
Площа фігур
Слайд #2
Площею многокутника називається величина внутрішньої області многокутника
Слайд #3
Площа чотирикутника
Чотирикутником називається фігура, яка складається з чотирьох точок і чотирьох відрізків, що послідовно їх сполучають. Дані точки називаються вершинами чотирикутника, а відрізки, що їх сполучають, - сторонами чотирикутника.
d2
d1
Чотирикутником називається фігура, яка складається з чотирьох точок і чотирьох відрізків, що послідовно їх сполучають. Дані точки називаються вершинами чотирикутника, а відрізки, що їх сполучають, - сторонами чотирикутника.
d2
d1
Слайд #4
Площа паралелограма
Паралелограм – це чотирикутник, у якого протилежні сторони паралельні, тобто лежать на паралельних прямих
ha
a
Паралелограм – це чотирикутник, у якого протилежні сторони паралельні, тобто лежать на паралельних прямих
ha
a
Слайд #5
Площа паралелограма
b
a
b
a
Слайд #6
Площа паралелограма
d1
d2
d1
d2
Слайд #7
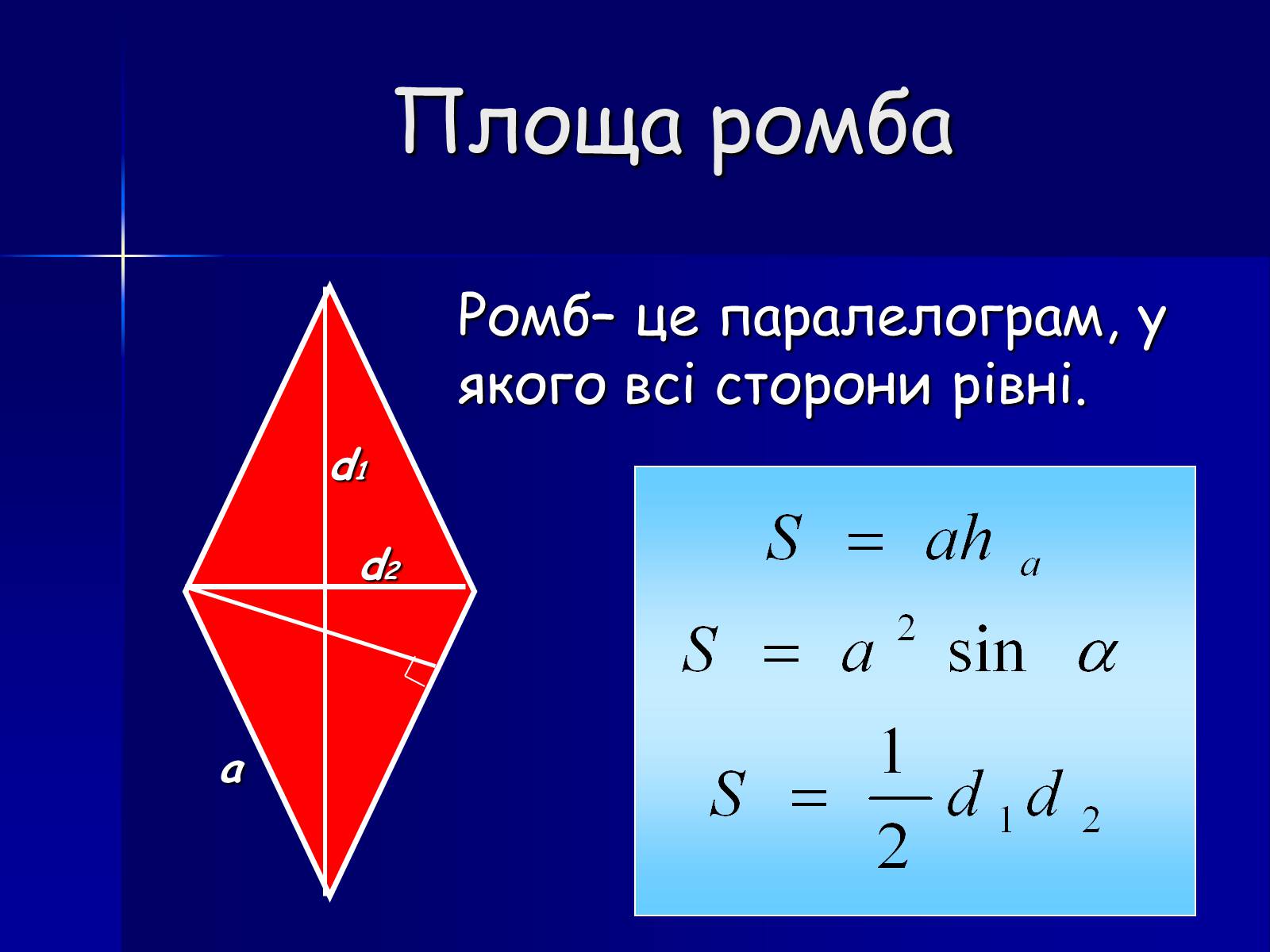
Площа ромба
Ромб– це паралелограм, у якого всі сторони рівні.
а
d1
d2
Ромб– це паралелограм, у якого всі сторони рівні.
а
d1
d2
Слайд #8
Площа прямокутника
S = ab
Прямокутник – паралелограм, у якого всі кути прямі
a
b
φ
d2
d1
S = ab
Прямокутник – паралелограм, у якого всі кути прямі
a
b
φ
d2
d1
Слайд #9
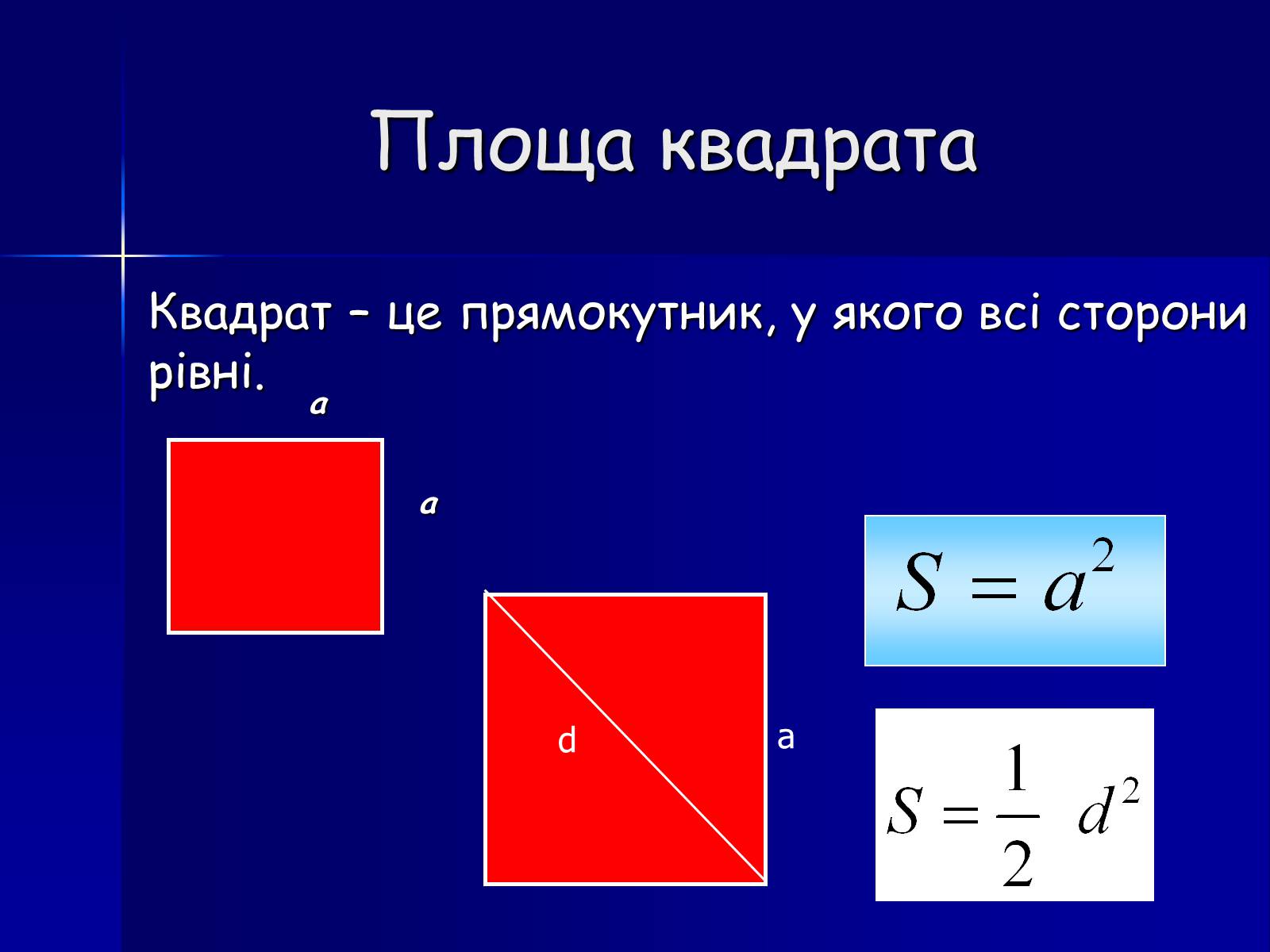
Площа квадрата
Квадрат – це прямокутник, у якого всі сторони рівні.
a
a
d
a
Квадрат – це прямокутник, у якого всі сторони рівні.
a
a
d
a
Слайд #10
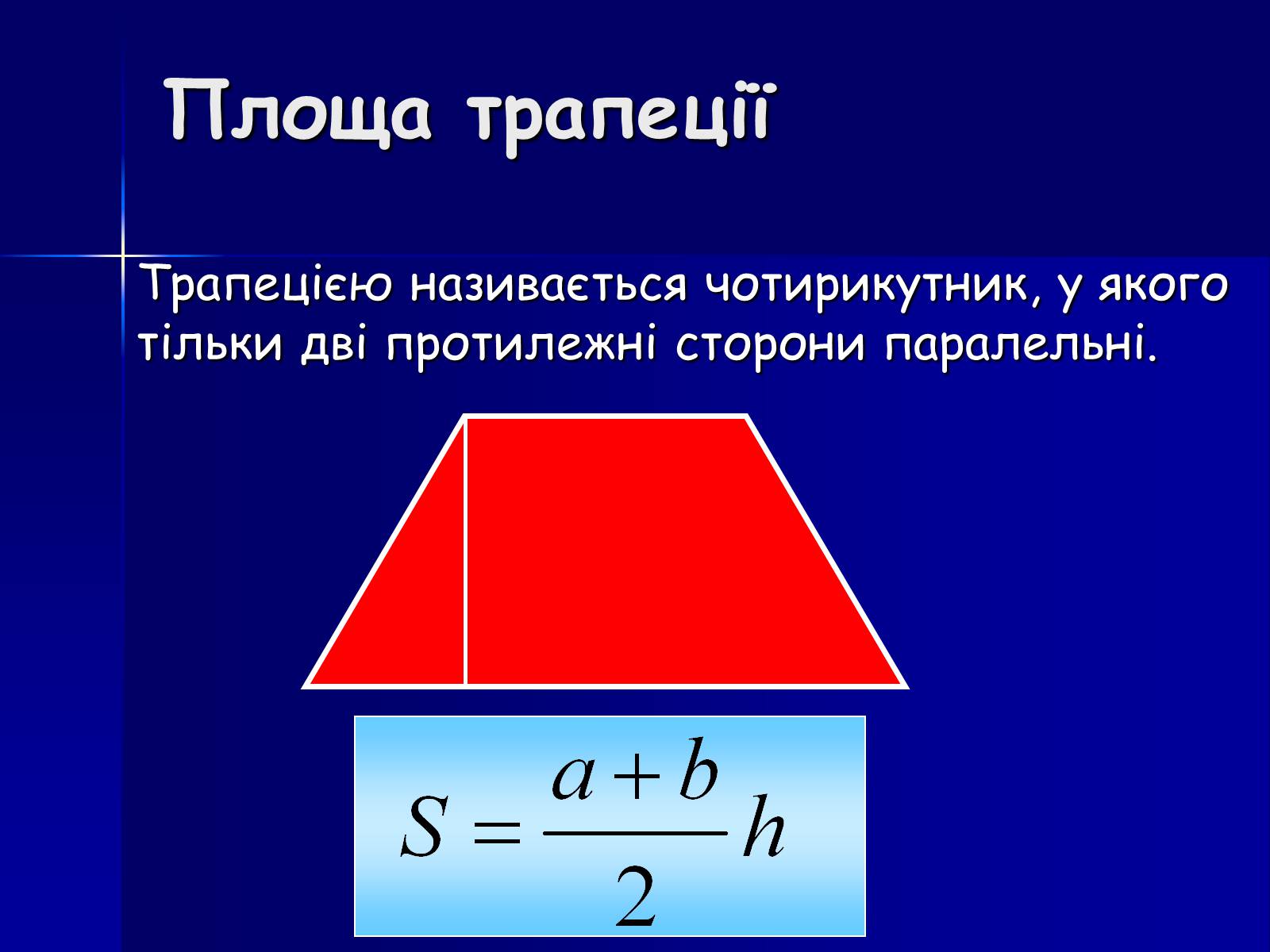
Площа трапеції
Трапецією називається чотирикутник, у якого тільки дві протилежні сторони паралельні.
Трапецією називається чотирикутник, у якого тільки дві протилежні сторони паралельні.
Слайд #11
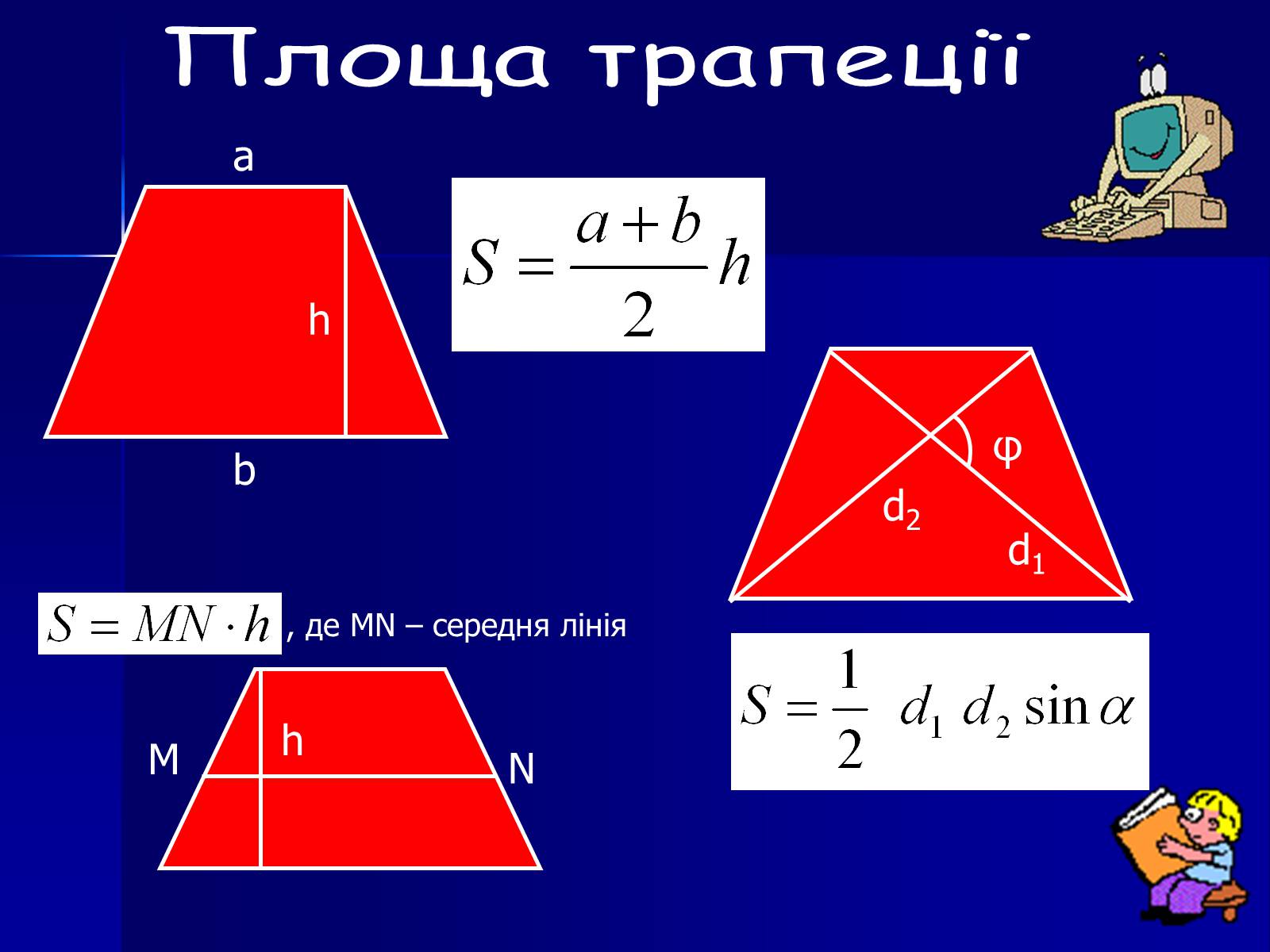
Площа трапеції
M
h
N
h
a
b
d1
d2
φ
, де MN – середня лінія
M
h
N
h
a
b
d1
d2
φ
, де MN – середня лінія
Слайд #12
Формули площ трикутників
a
ha
a
b
a
ha
a
b
Слайд #13
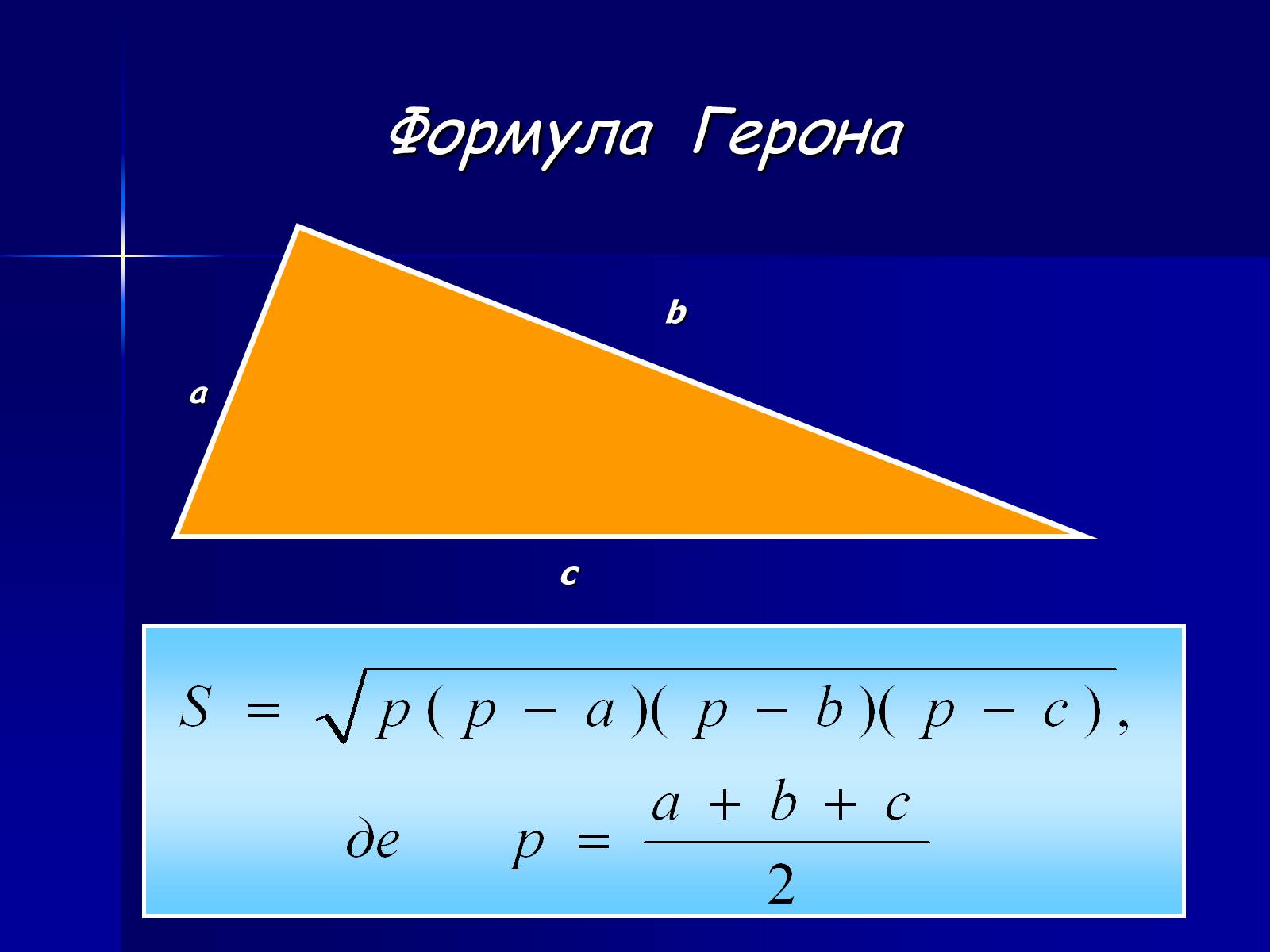
Формула Герона
b
a
c
b
a
c
Слайд #14
прямокутний трикутник
рівносторонній трикутник
b
a
a
назад
рівносторонній трикутник
b
a
a
назад
Слайд #15
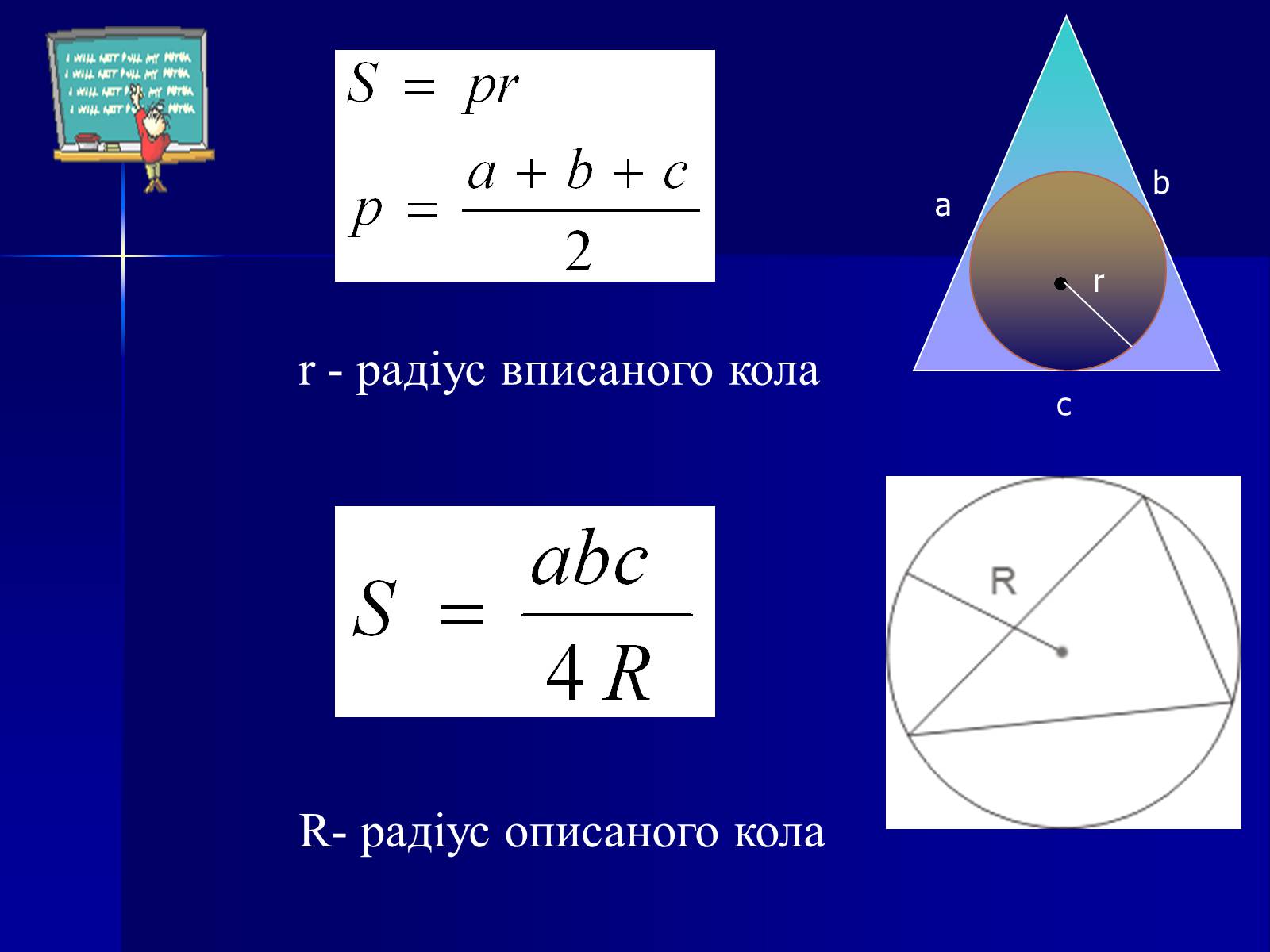
r - радіус вписаного кола
a
c
b
r
R- радіус описаного кола
a
c
b
r
R- радіус описаного кола
Слайд #16
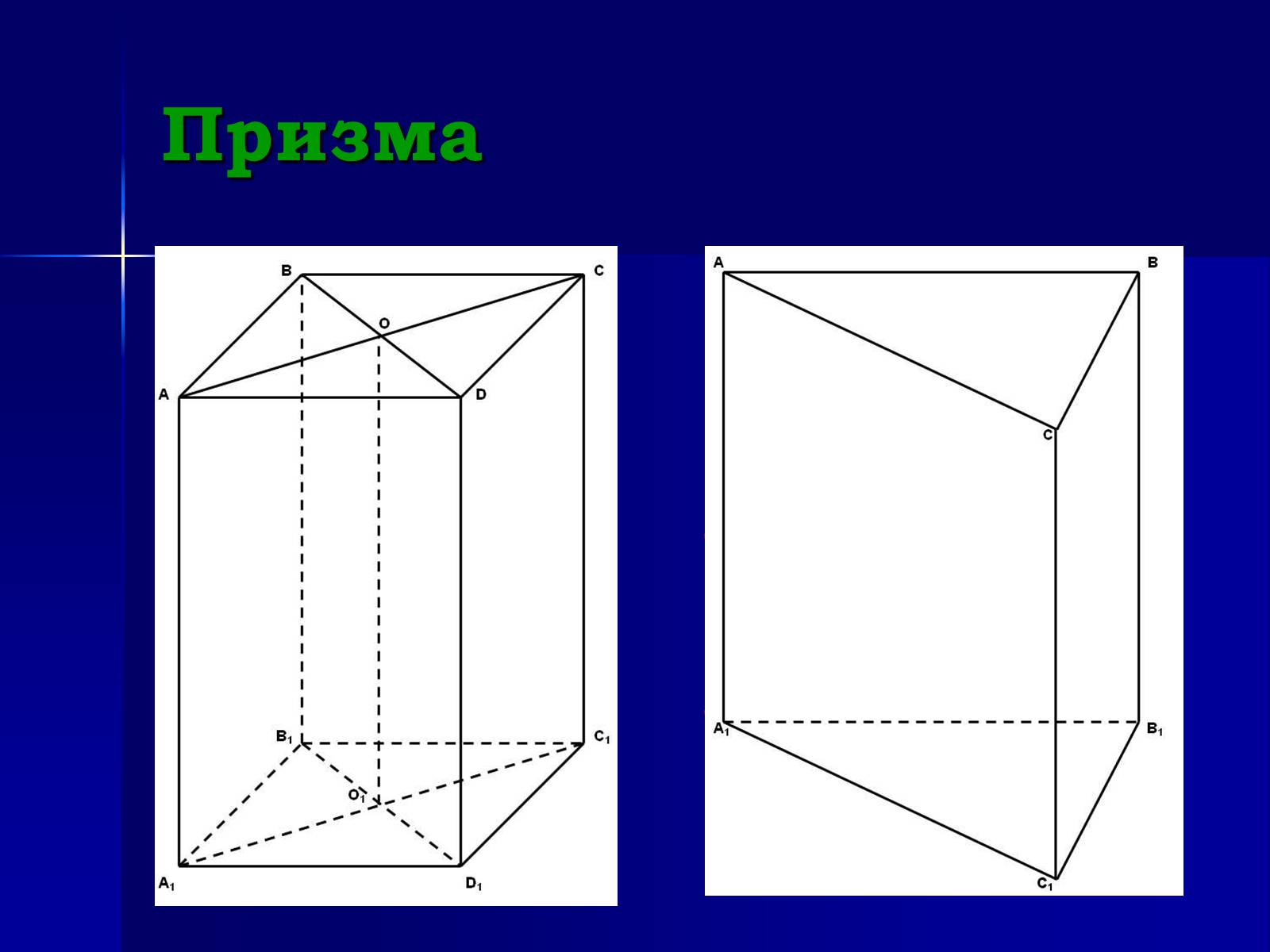
Призма
V = Sосн.• H
Sбіч.= Pосн. • H
Sп.п.= Sбіч.+ 2•Sосн.
V = Sосн.• H
Sбіч.= Pосн. • H
Sп.п.= Sбіч.+ 2•Sосн.
Слайд #17
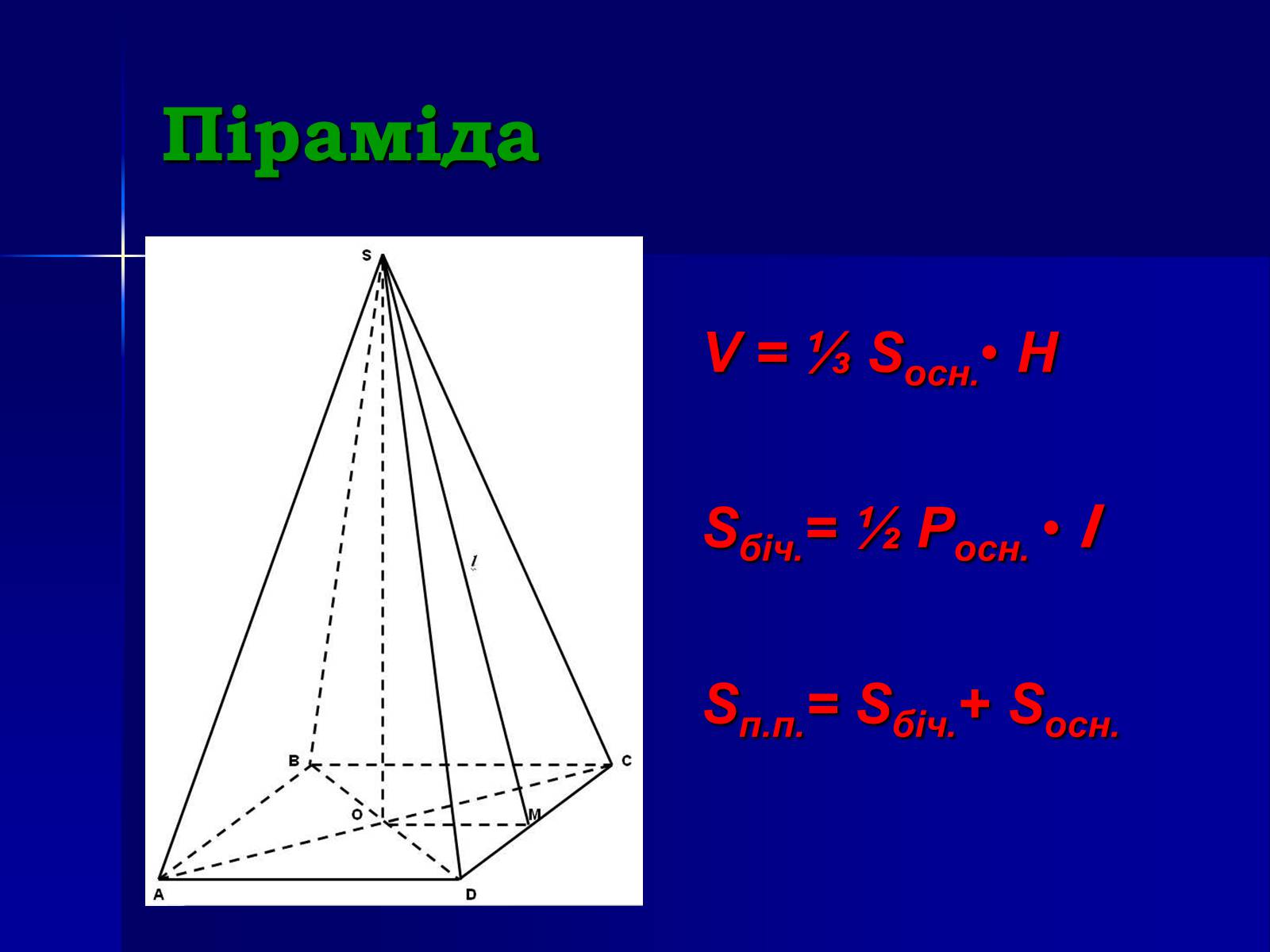
Піраміда
V = ⅓ Sосн.• H
Sбіч.= ½ Pосн. • l
Sп.п.= Sбіч.+ Sосн.
V = ⅓ Sосн.• H
Sбіч.= ½ Pосн. • l
Sп.п.= Sбіч.+ Sосн.
Слайд #18
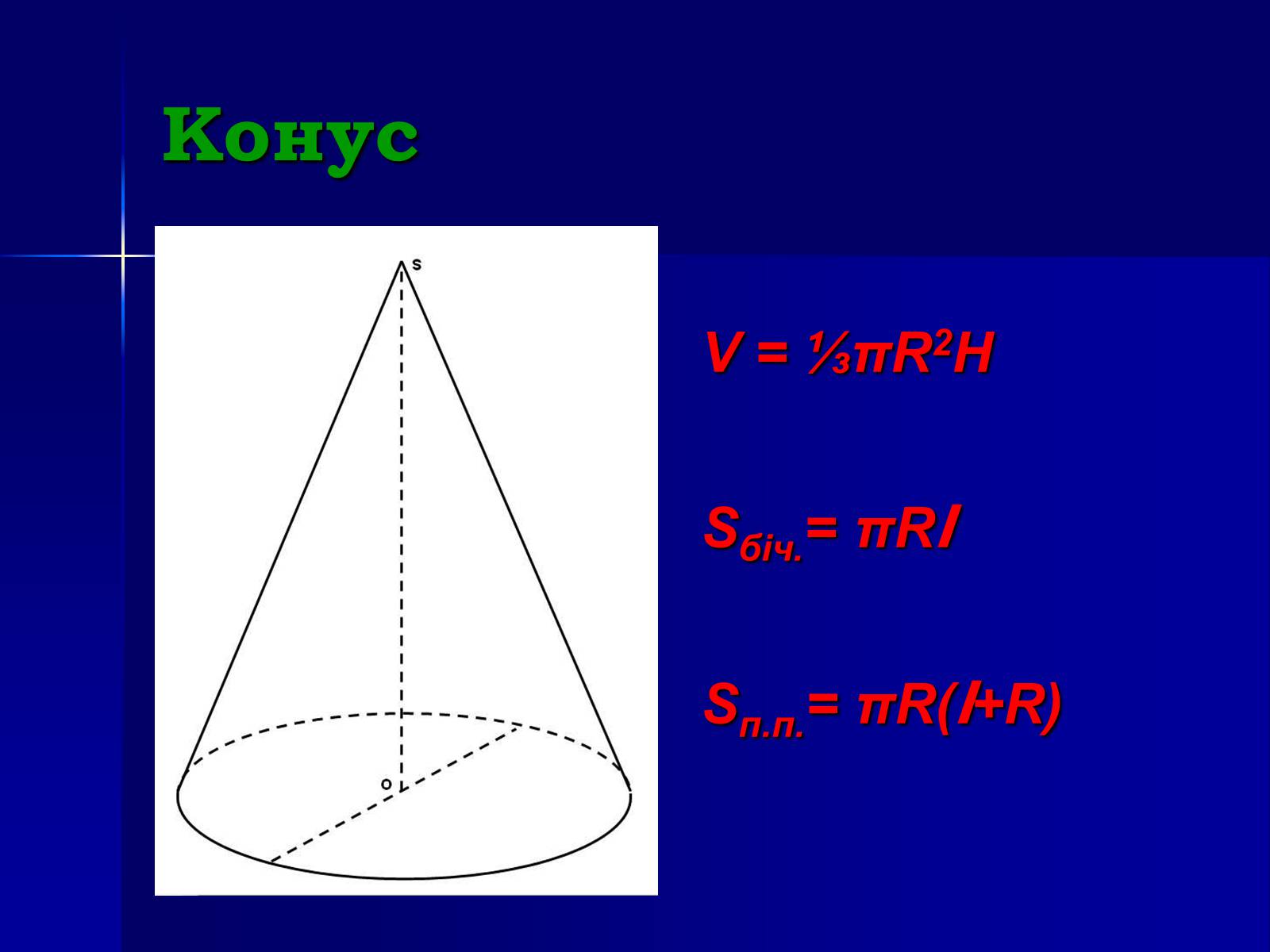
Конус
V = ⅓πR2H
Sбіч.= πRl
Sп.п.= πR(l+R)
V = ⅓πR2H
Sбіч.= πRl
Sп.п.= πR(l+R)
Слайд #19
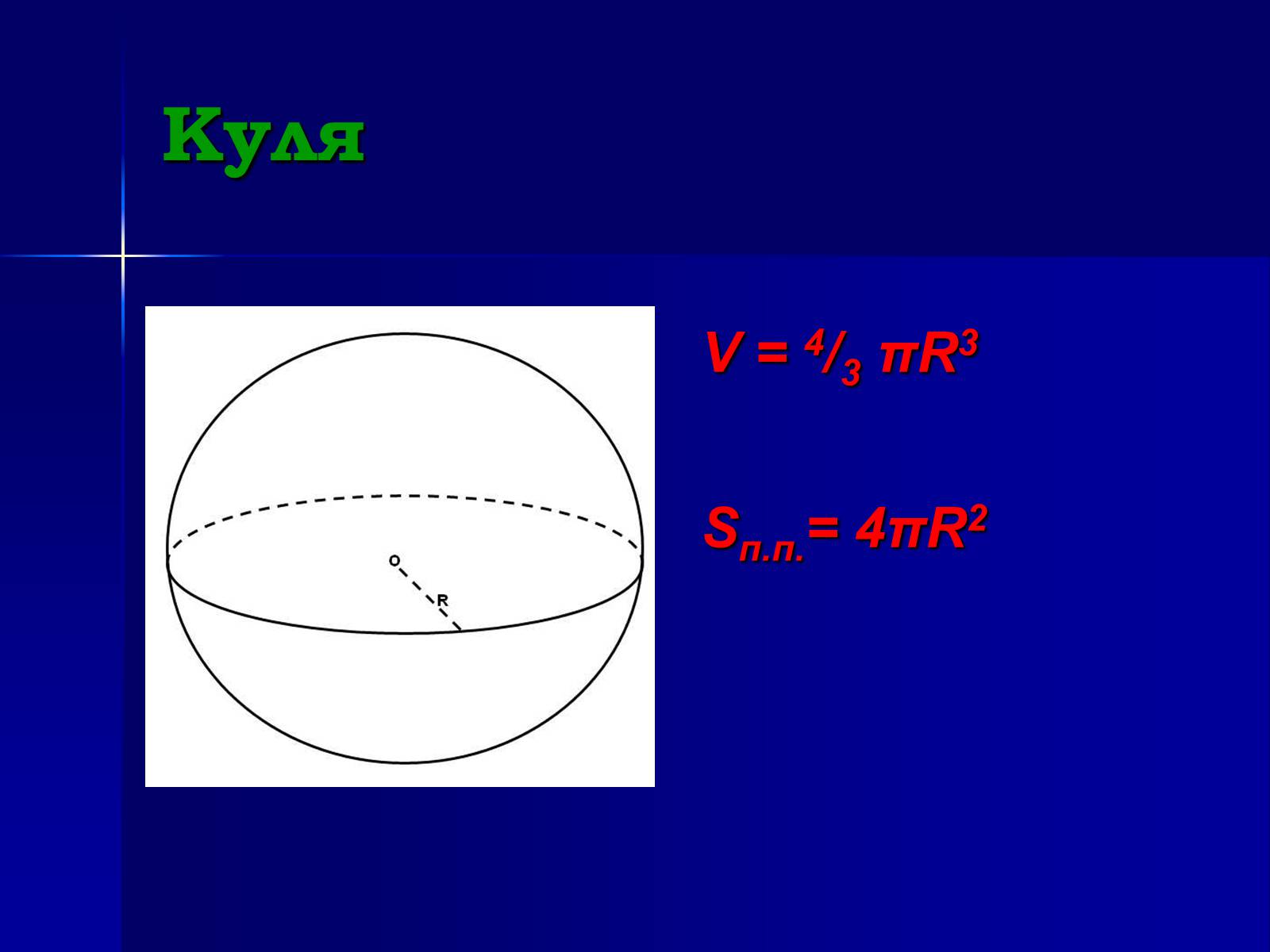
Куля
V = 4/3 πR3
Sп.п.= 4πR2
V = 4/3 πR3
Sп.п.= 4πR2
Слайд #20
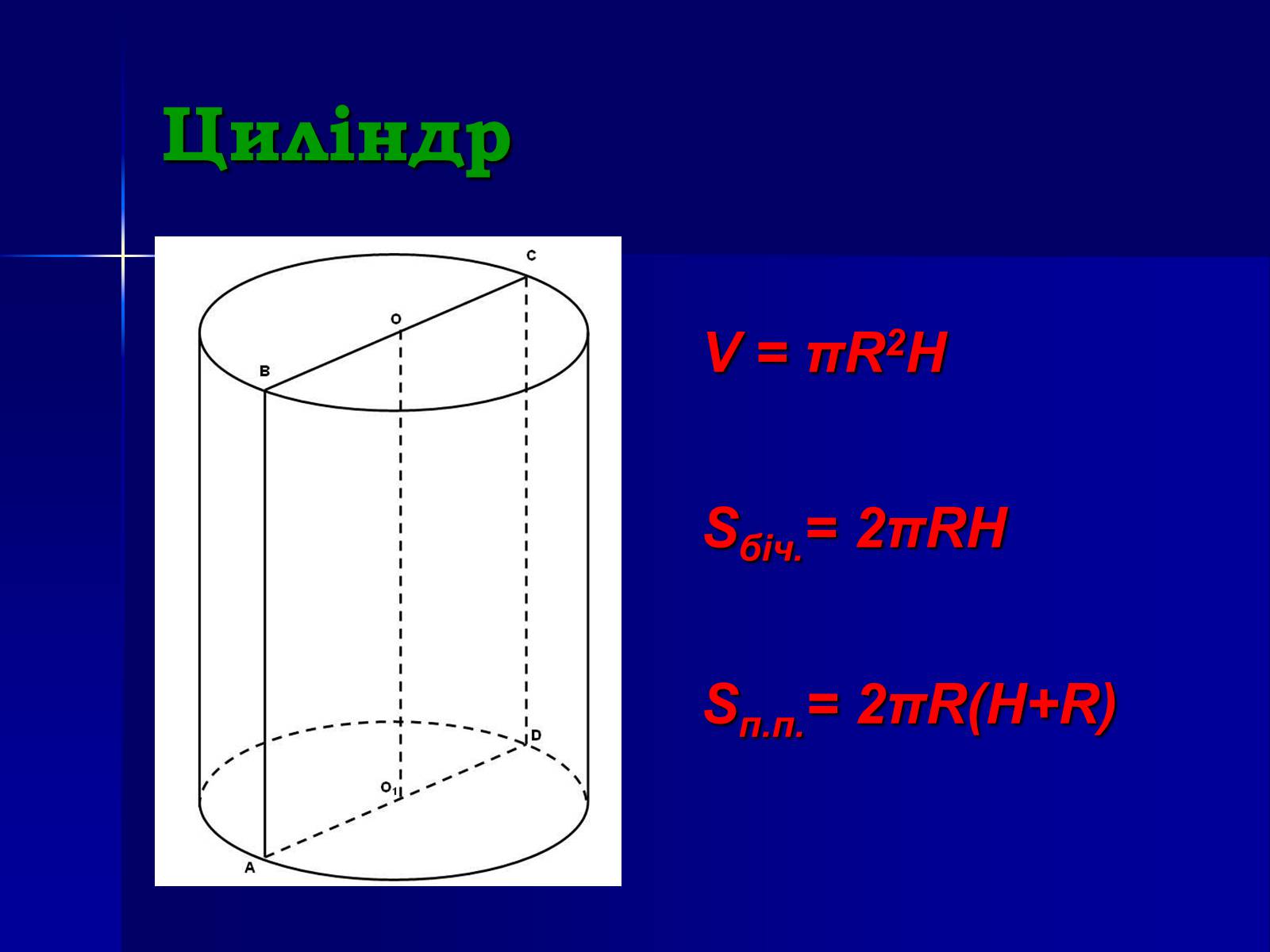
Циліндр
V = πR2H
Sбіч.= 2πRH
Sп.п.= 2πR(H+R)
V = πR2H
Sбіч.= 2πRH
Sп.п.= 2πR(H+R)
