- Головна
- Готові шкільні презентації
- Презентація на тему «Циліндр» (варіант 2)
Презентація на тему «Циліндр» (варіант 2)
301
Слайд #1
Автор презентації – Лукан Ростислав. Усі права захищені. Несанкціоноване копіювання та розповсюдження карається Господом Богом

Слайд #2
Цилі́ндр (грец.κύλινδρος — «валик») —
Геометричне тіло, обмежене замкнутою циліндричною поверхнею і двома паралельними площинами, що перетинають її.
Геометричне тіло, обмежене замкнутою циліндричною поверхнею і двома паралельними площинами, що перетинають її.

Слайд #3
Цилі́ндр (грец.κύλινδρος — «валик») —
Геометричне тіло, обмежене замкнутою циліндричною поверхнею і двома паралельними площинами, що перетинають її.
Геометричне тіло, обмежене замкнутою циліндричною поверхнею і двома паралельними площинами, що перетинають її.
Слайд #4
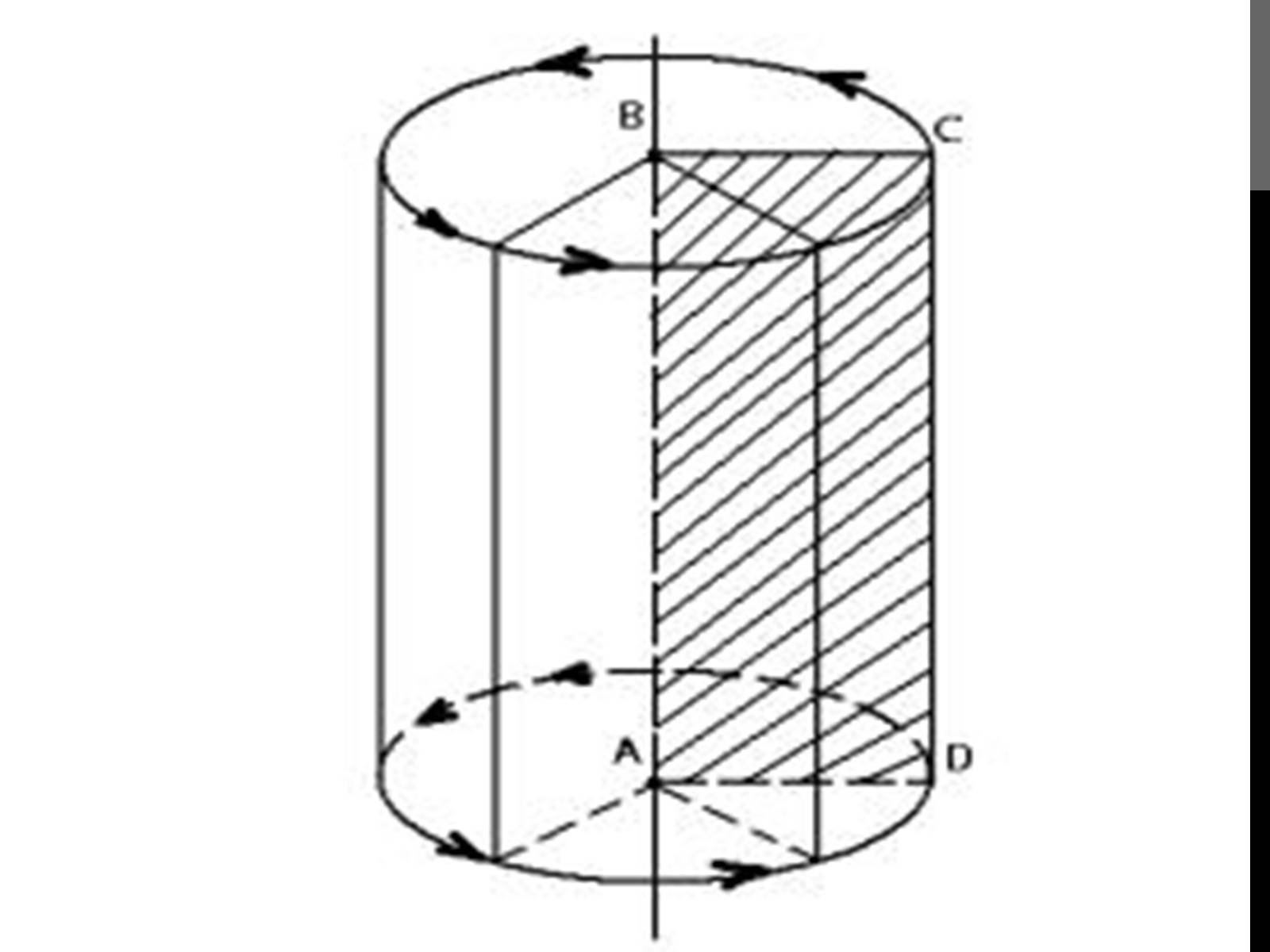
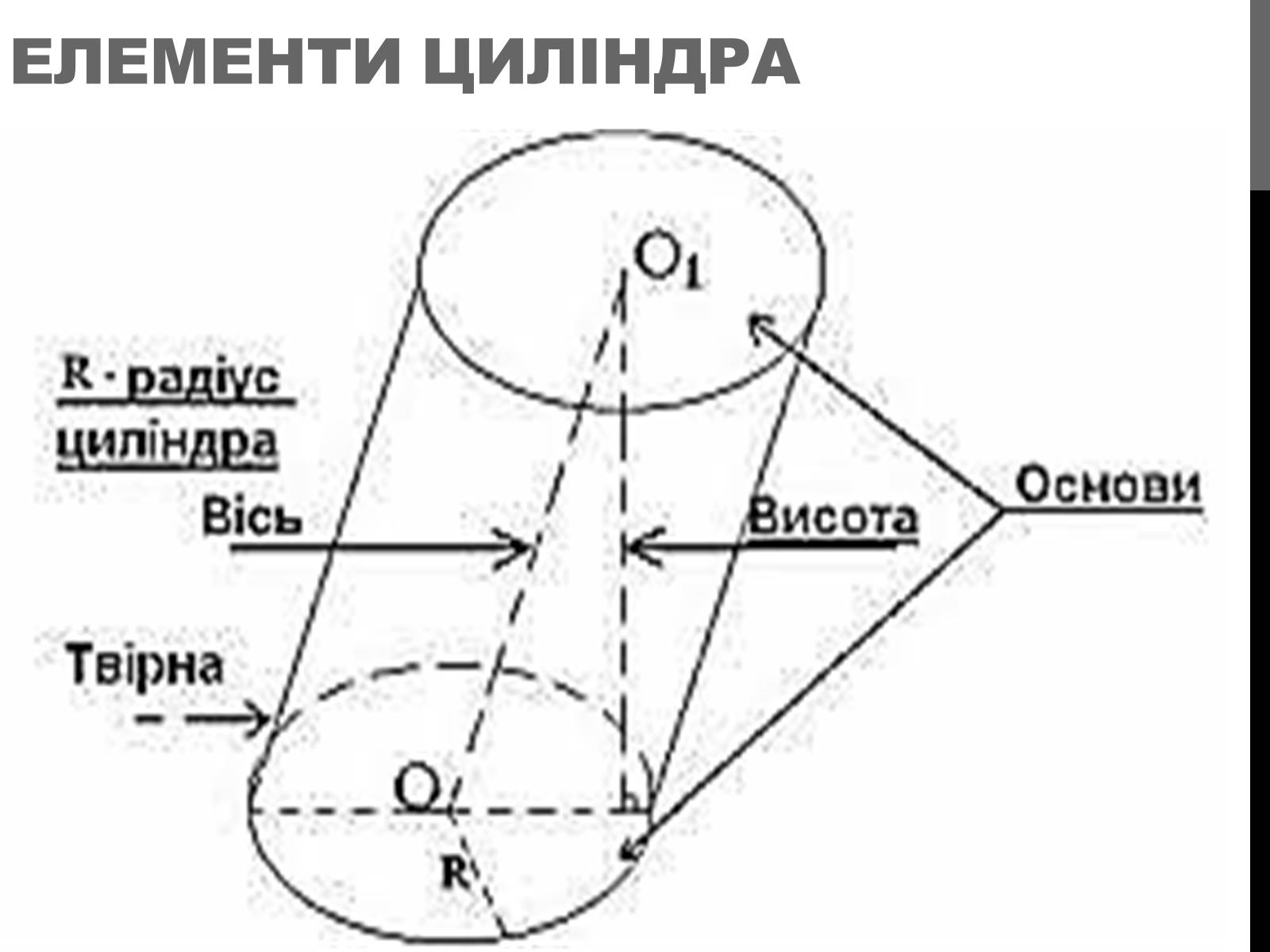
Елементи циліндра
Слайд #5
Основи – рівні круги, що лежать в паралельних площинах
Твірні циліндра — відрізки, що сполучають відповідні точки кіл кругів. Вони паралельні і рівні між собою.
Поверхня циліндра ― основа і бічнна поверхня.
Бічна поверхня складається з твірних.
Радіус циліндра ― радіус його основи.
Висота циліндра ― відстань між площинами основ.
Вісь циліндра ― пряма, яка проходить через центри основ. Вона паралельна твірним.
Осьовий переріз — переріз циліндра площиною, яка проходить через вісь циліндра.
Дотична до циліндра — площина, яка проходить через твірну прямого циліндра і перпендикулярна до осьового перерізу, проведеного через цю твірну, називається площиною.
Циліндр називається прямим, якщо його твірні перпендикулярні до площин основ. Прямий циліндр можна розглядати як тіло, утворене обертанням прямокутника навколо його сторони як осі.
Твірні циліндра — відрізки, що сполучають відповідні точки кіл кругів. Вони паралельні і рівні між собою.
Поверхня циліндра ― основа і бічнна поверхня.
Бічна поверхня складається з твірних.
Радіус циліндра ― радіус його основи.
Висота циліндра ― відстань між площинами основ.
Вісь циліндра ― пряма, яка проходить через центри основ. Вона паралельна твірним.
Осьовий переріз — переріз циліндра площиною, яка проходить через вісь циліндра.
Дотична до циліндра — площина, яка проходить через твірну прямого циліндра і перпендикулярна до осьового перерізу, проведеного через цю твірну, називається площиною.
Циліндр називається прямим, якщо його твірні перпендикулярні до площин основ. Прямий циліндр можна розглядати як тіло, утворене обертанням прямокутника навколо його сторони як осі.

Слайд #6
Види циліндрів
Нескінченний циліндр — це нескінченне тіло, обмежене замкнутою нескінченною циліндричною поверхнею.
Відкритий циліндр — обмежене замкнутим циліндровим променем і його основою геометричне тіло.
Основи циліндра якісно впливають на циліндр:
якщо основи циліндра пласкі (і, отже, що містять їх площині рівнобіжні) — циліндр називають таким, що стоїть на площині;
якщо основи стоять на площині циліндра перпендикулярні твірним — прямий циліндр; зокрема, якщо основа що стоїть на площині циліндра:
коло — круглий циліндр;
еліпс — еліптичний циліндр.
Нескінченний циліндр — це нескінченне тіло, обмежене замкнутою нескінченною циліндричною поверхнею.
Відкритий циліндр — обмежене замкнутим циліндровим променем і його основою геометричне тіло.
Основи циліндра якісно впливають на циліндр:
якщо основи циліндра пласкі (і, отже, що містять їх площині рівнобіжні) — циліндр називають таким, що стоїть на площині;
якщо основи стоять на площині циліндра перпендикулярні твірним — прямий циліндр; зокрема, якщо основа що стоїть на площині циліндра:
коло — круглий циліндр;
еліпс — еліптичний циліндр.

Слайд #7
площа
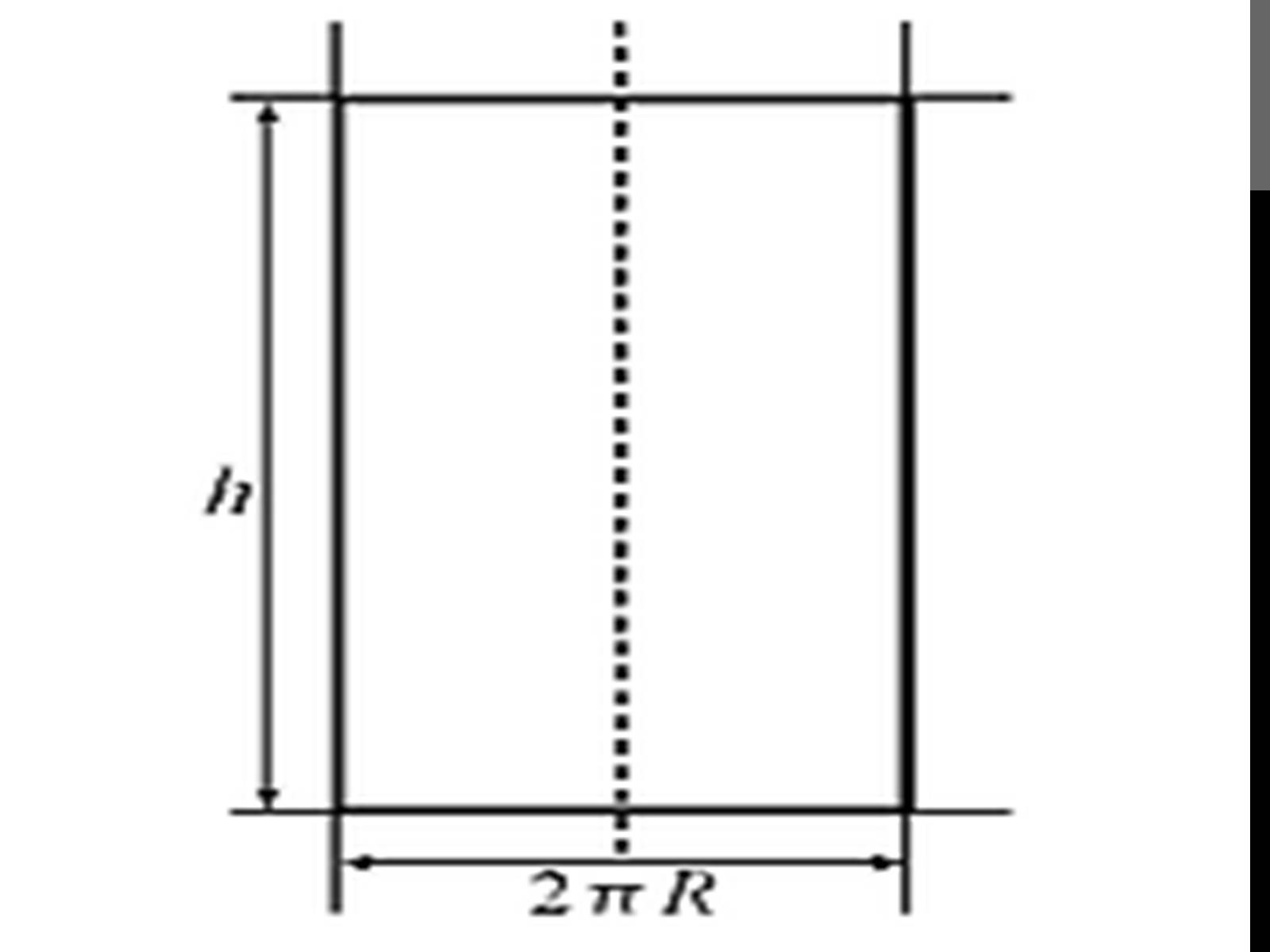
Площа бічної поверхні
тіл обертання обчислюється за їхньою розгорткою. Розгортка циліндра - прямокутник з висотою і довжиною , отже площа бічної поверхні циліндра дорівнює площі його розгортки та обчислюється за формулою:
S(біч)Де – сторона а прямокутника, а висота – сторона в
Площа бічної поверхні
тіл обертання обчислюється за їхньою розгорткою. Розгортка циліндра - прямокутник з висотою і довжиною , отже площа бічної поверхні циліндра дорівнює площі його розгортки та обчислюється за формулою:
S(біч)Де – сторона а прямокутника, а висота – сторона в

Слайд #8
площа
Площа бічної поверхні
тіл обертання обчислюється за їхньою розгорткою. Розгортка циліндра - прямокутник з висотою і довжиною , отже площа бічної поверхні циліндра дорівнює площі його розгортки та обчислюється за формулою:
S(біч)Де – сторона а прямокутника, а висота – сторона в
Площа бічної поверхні
тіл обертання обчислюється за їхньою розгорткою. Розгортка циліндра - прямокутник з висотою і довжиною , отже площа бічної поверхні циліндра дорівнює площі його розгортки та обчислюється за формулою:
S(біч)Де – сторона а прямокутника, а висота – сторона в
Слайд #9
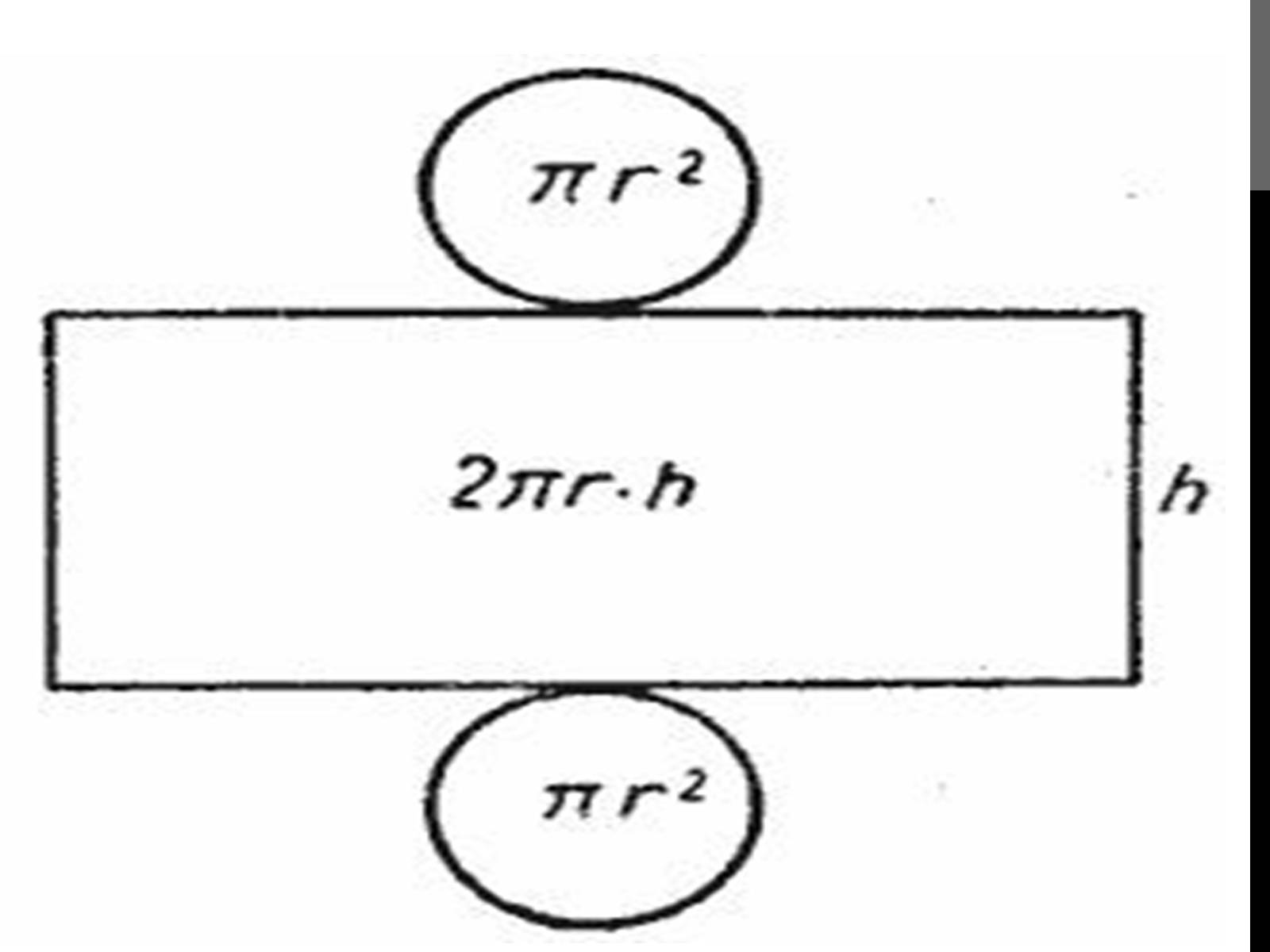
Площа основ
Площу основ можливо обчислити вельми простою формулою,адже основа – коло:
S(осн)
Площу основ можливо обчислити вельми простою формулою,адже основа – коло:
S(осн)

Слайд #10
Площа основ
Площу основ можливо обчислити вельми простою формулою,адже основа – коло:
S(осн)
Площу основ можливо обчислити вельми простою формулою,адже основа – коло:
S(осн)
Слайд #11
Об'єм
V
V=
V
V=
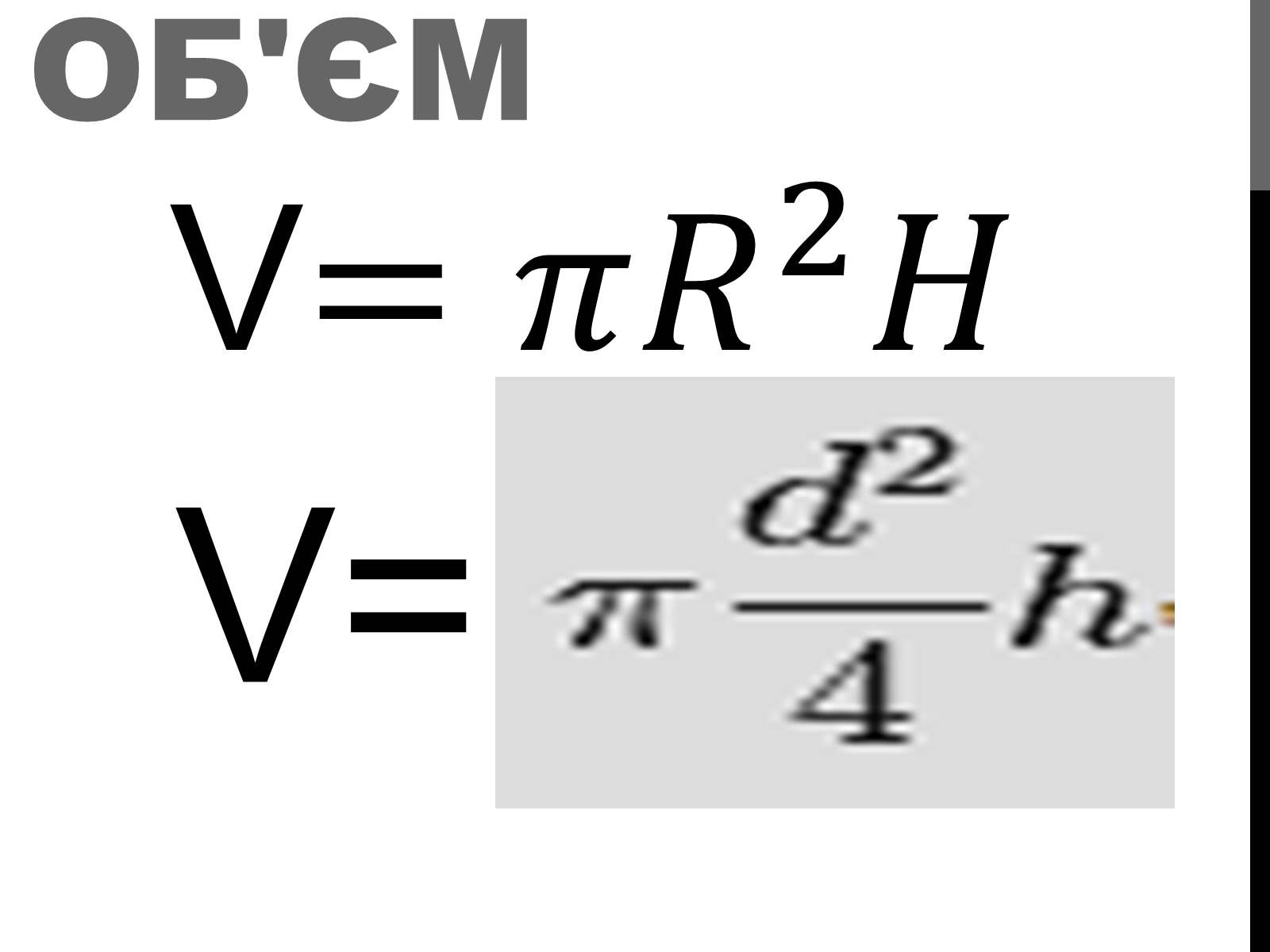
Слайд #12
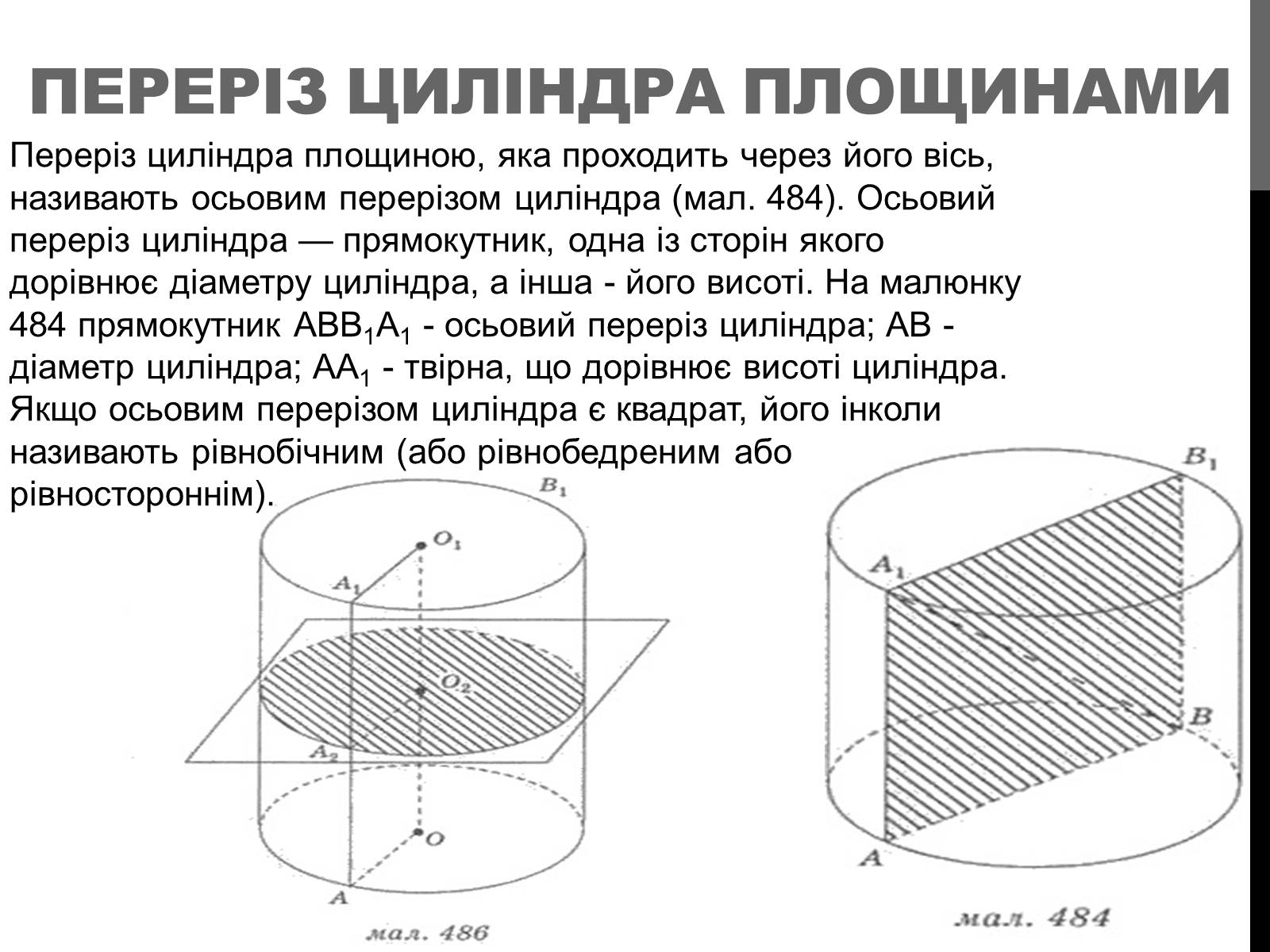
Переріз циліндра площинами
Переріз циліндра площиною, яка проходить через його вісь, називають осьовим перерізом циліндра (мал. 484). Осьовий переріз циліндра — прямокутник, одна із сторін якого дорівнює діаметру циліндра, а інша - його висоті. На малюнку 484 прямокутник АВВ1А1 - осьовий переріз циліндра; АВ - діаметр циліндра; АА1 - твірна, що дорівнює висоті циліндра. Якщо осьовим перерізом циліндра є квадрат, його інколи називають рівнобічним (або рівнобедреним або рівностороннім).
Переріз циліндра площиною, яка проходить через його вісь, називають осьовим перерізом циліндра (мал. 484). Осьовий переріз циліндра — прямокутник, одна із сторін якого дорівнює діаметру циліндра, а інша - його висоті. На малюнку 484 прямокутник АВВ1А1 - осьовий переріз циліндра; АВ - діаметр циліндра; АА1 - твірна, що дорівнює висоті циліндра. Якщо осьовим перерізом циліндра є квадрат, його інколи називають рівнобічним (або рівнобедреним або рівностороннім).
Слайд #13
Так казав заратустра!

Слайд #14
Так казав заратустра!

Слайд #15
Так казав заратустра!

Слайд #16
Так казав заратустра!

Слайд #17
Так казав заратустра!

Слайд #18
