- Головна
- Готові шкільні презентації
- Презентація на тему «Застосування похідної в різних сферах життя людини»
Презентація на тему «Застосування похідної в різних сферах життя людини»
500
Слайд #1
Застосування похідної в різних сферах життя людини

Слайд #2
Похідна́ — основне поняття диференціального числення, що характеризує швидкість зміни функції. Визначається як границя відношення приросту функції до приросту її аргументу коли приріст аргументу прямує до нуля (якщо така границя існує).
Визначення
Визначення

Слайд #3
Похідна у географії

Слайд #4
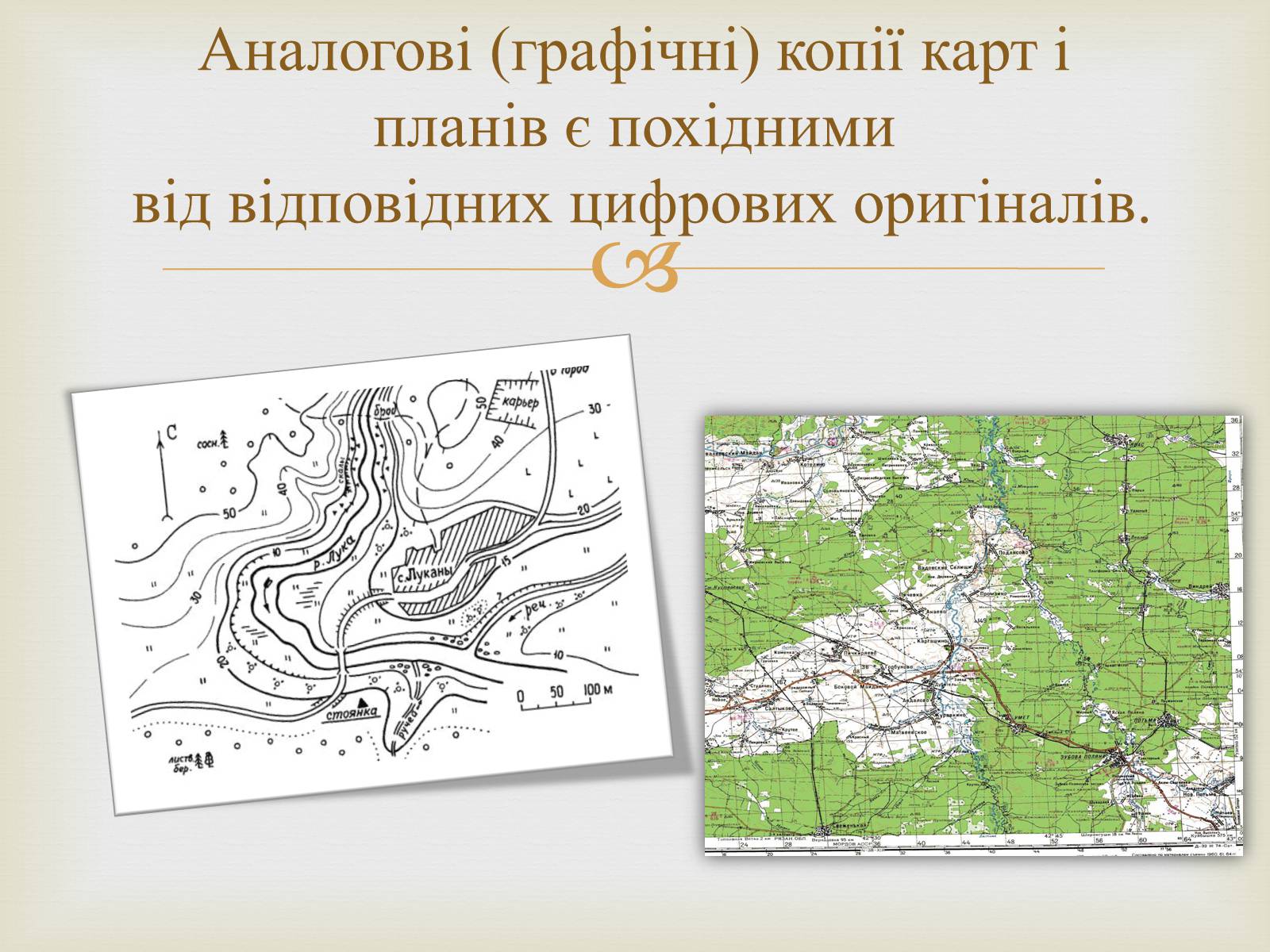
Аналогові (графічні) копії карт і планів є похідними від відповідних цифрових оригіналів.
Слайд #5
Ідея соціологічної моделі Томаса Мальтуса полягає в тому, що приріст населення пропорційно числу населення в даний момент часу t через N (t).Модель Мальтуса непогано діяла для опису чисельності населення США з 1790 по 1860 роки. Нині ця модель в більшості країн не діє.
Чисельність населення
Чисельність населення

Слайд #6
Похідна в географії поєднується з багатьма її галузями (сейсмографія, розміщення і чисельність населення), а також з економічної географії. Все це дозволяє повніше вивчати розвиток населення і країн світу.
Висновок
Висновок

Слайд #7
Похідна в хімії

Слайд #8
Похідну в хімії використовують для визначення дуже важливої речі - швидкості хімічної реакції, одного з вирішальних факторів, який потрібно враховувати в багатьох областях науково-виробничої діяльності.
Вступ
Вступ

Слайд #9
Якщо P (t) - закон зміни кількості речовини, вступило в хімічну реакцію, то швидкість v (t) хімічної реакції в момент часу t дорівнює похідній:
Формула похідної в хімії
V (t) = p ‘(t)
Формула похідної в хімії
V (t) = p ‘(t)

Слайд #10
Похідна в біології

Слайд #11
Для прикладу використання похідної в сферах біології розглянемо на прикладі розв'язку даної задачі:
З відомої залежності чисельності популяції x(t) визначити відносний приріст в момент часу t.
Приклад
З відомої залежності чисельності популяції x(t) визначити відносний приріст в момент часу t.
Приклад

Слайд #12
Поняття мовою біології
Позначення
Понятие мовою математики
Чисельність в момент часу t1
x = x(t)
Функція
Інтервал часу
∆t = t2 – t1
Приріст аргументу
Зміна чисельності популяції
∆x = x(t2) – x(t1)
Приріст функції
Швидкість зміни чисельності популяції
∆x/∆t
Відношення приросту функції до приросту аргументу
Відносний приріст в даний момент
Похідна
Розв'язання
Р = х‘ (t)
Позначення
Понятие мовою математики
Чисельність в момент часу t1
x = x(t)
Функція
Інтервал часу
∆t = t2 – t1
Приріст аргументу
Зміна чисельності популяції
∆x = x(t2) – x(t1)
Приріст функції
Швидкість зміни чисельності популяції
∆x/∆t
Відношення приросту функції до приросту аргументу
Відносний приріст в даний момент
Похідна
Розв'язання
Р = х‘ (t)

Слайд #13
Похідна в фізиці

Слайд #14
Швидкість матеріальної точки
Миттєва швидкість як фізичний зміст похідної
Миттєве значення сили змінного струму
Миттєве значення ЕРС електромагнітної індукції
Максимальна потужність
Визначення похідної у фізиці
Миттєва швидкість як фізичний зміст похідної
Миттєве значення сили змінного струму
Миттєве значення ЕРС електромагнітної індукції
Максимальна потужність
Визначення похідної у фізиці

Слайд #15
Фізичний зміст похідної x' (t) від неперервної функції x (t) в точці t0 – це миттєва швидкість зміни величини функції, за умови, що зміна аргументу Δt прямує до нуля.
Миттєва швидкість (величина шляху, пройденого за мить) і є похідна величина від функції, що описує шлях літака за часом. Миттєва швидкість - це і є фізичний зміст похідної.
Миттєва швидкість як фізичний зміст похідної
Миттєва швидкість (величина шляху, пройденого за мить) і є похідна величина від функції, що описує шлях літака за часом. Миттєва швидкість - це і є фізичний зміст похідної.
Миттєва швидкість як фізичний зміст похідної

Слайд #16
Наприклад, при електромагнітних коливаннях, що виникають у коливальному контурі заряд на обкладинках конденсатора змінюється за законом:
тоді
Миттєве значення сили змінного струму
тоді
Миттєве значення сили змінного струму
