- Головна
- Готові шкільні презентації
- Презентація на тему «Центральна симетрія»
Презентація на тему «Центральна симетрія»
276
Слайд #1
Центральна симетрія
Виконала учениця 9 - В класу
Повстянко Катерина
Виконала учениця 9 - В класу
Повстянко Катерина

Слайд #2
Історична довідка
Естетична забарвленість симетрії в найбільш загальномурозумінні - це узгодженість або врівноваженість окремих частин об'єкта,об'єднаних в єдине ціле, гармонія пропорцій. Симетрія проявляється нетільки в розумінні геометричної будови тіл в природі, але й в ряді областейлюдської діяльності. У мистецтві симетрія може проявитися впропорційності і взаємоп
В Епоху Відродження з'явилися
перші фундаментальні дослідження з
теорії перспективи, зокрема роботи
видатних художників Леонардо да Вінчі
(1452-1519) і Альбрехта Дюрера
(1471-1528). Розробником математичних основ теорії проективних перетворень(теорії перспективи) став французький інженер і архітектор Жерар Дезарг (1593-1662).
Естетична забарвленість симетрії в найбільш загальномурозумінні - це узгодженість або врівноваженість окремих частин об'єкта,об'єднаних в єдине ціле, гармонія пропорцій. Симетрія проявляється нетільки в розумінні геометричної будови тіл в природі, але й в ряді областейлюдської діяльності. У мистецтві симетрія може проявитися впропорційності і взаємоп
В Епоху Відродження з'явилися
перші фундаментальні дослідження з
теорії перспективи, зокрема роботи
видатних художників Леонардо да Вінчі
(1452-1519) і Альбрехта Дюрера
(1471-1528). Розробником математичних основ теорії проективних перетворень(теорії перспективи) став французький інженер і архітектор Жерар Дезарг (1593-1662).

Слайд #3
Альбрехт Дюрер
Гаспар Монж
Леонардо да Вінчі
Мішель Шаль
Гаспар Монж
Леонардо да Вінчі
Мішель Шаль

Слайд #4
А
А1
О
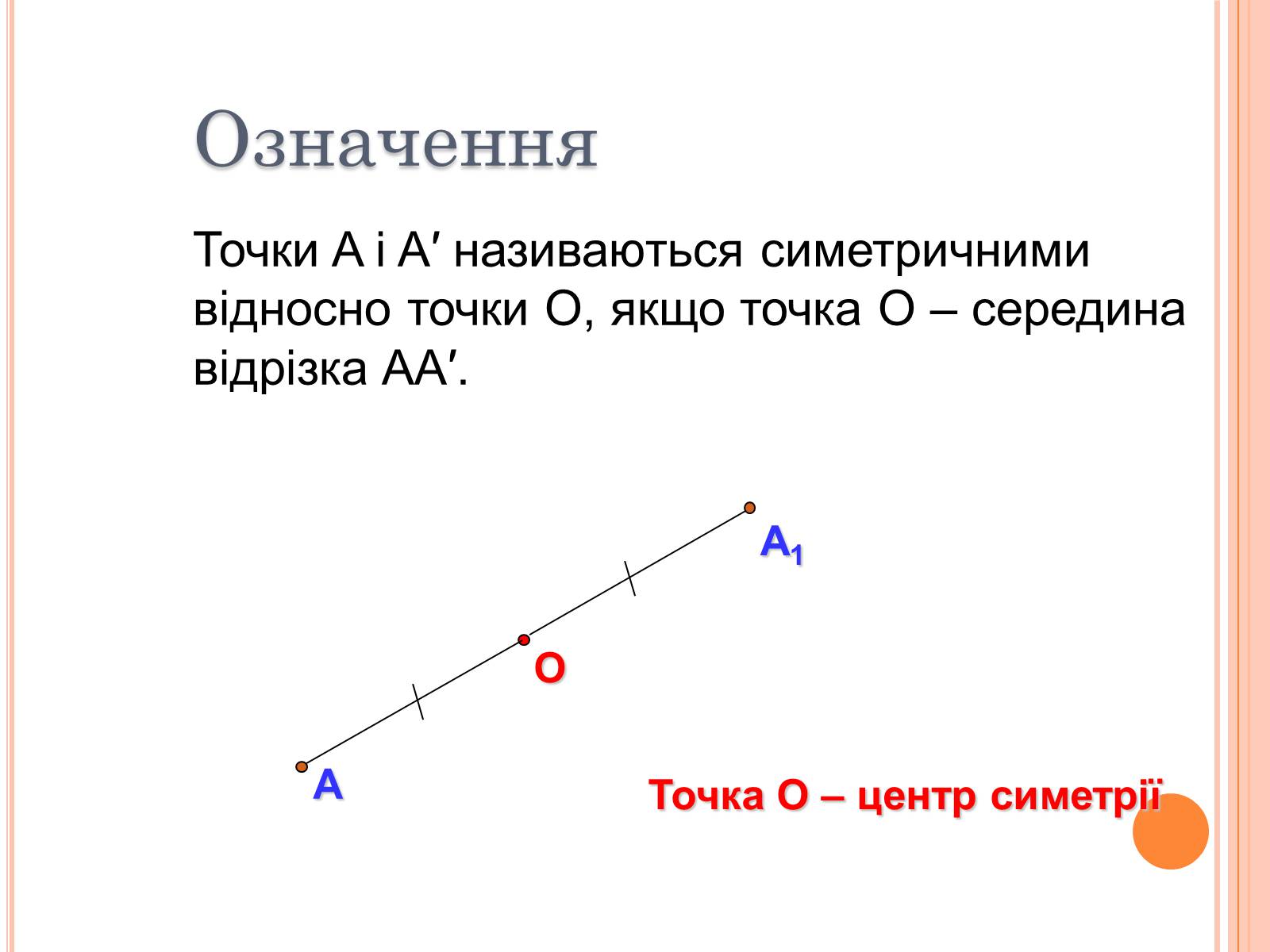
Точки A і A′ називаються симетричними відносно точки О, якщо точка О – середина відрізка AA′.
Точка О – центр симетрії
Означення
А1
О
Точки A і A′ називаються симетричними відносно точки О, якщо точка О – середина відрізка AA′.
Точка О – центр симетрії
Означення
Слайд #5
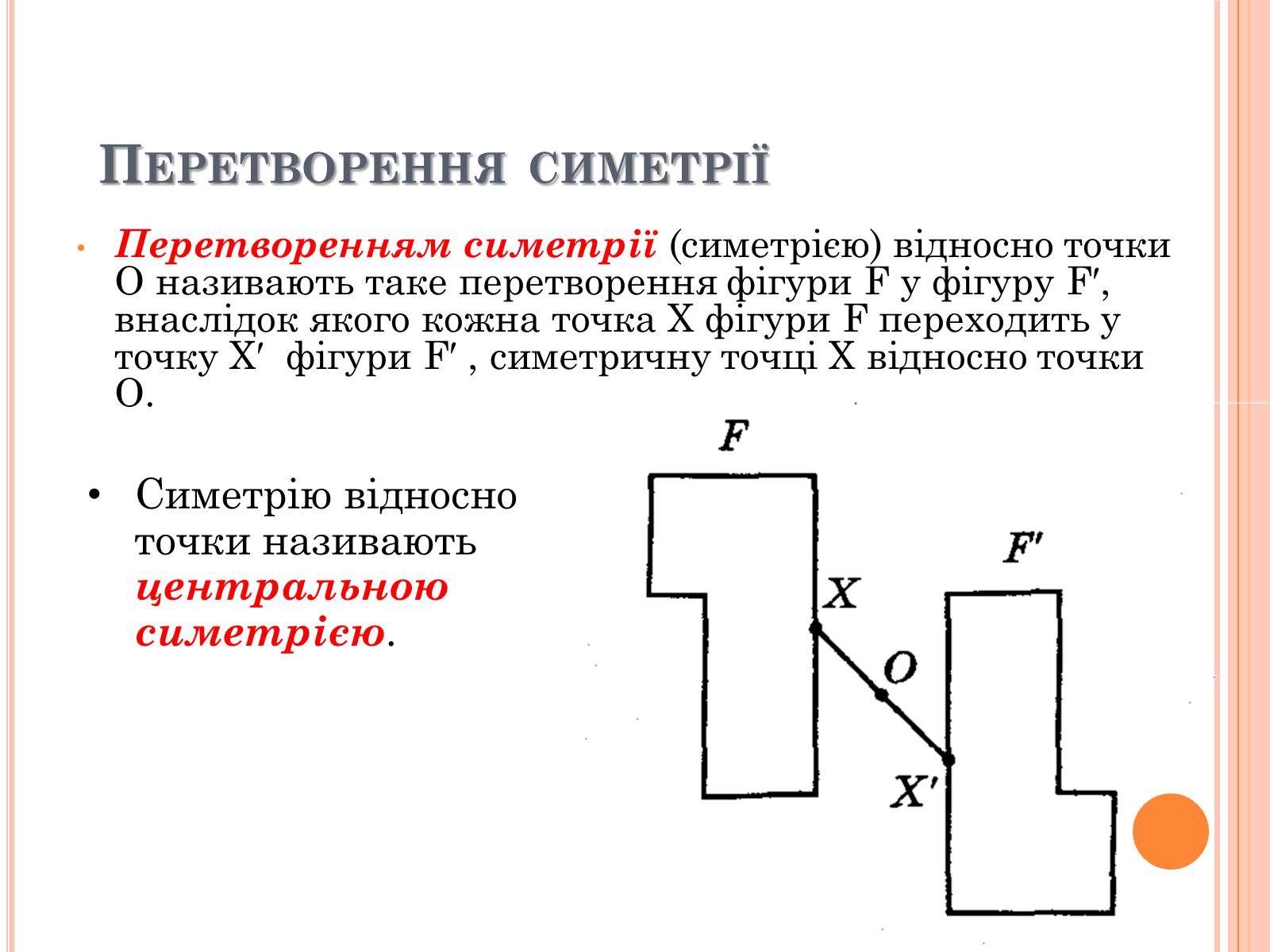
Перетворення симетрії
Перетворенням симетрії (симетрією) відносно точки О називають таке перетворення фігури F у фігуру F′, внаслідок якого кожна точка Х фігури F переходить у точку Х′ фігури F′ , симетричну точці Х відносно точки О.
Симетрію відносно точки називають центральною симетрією.
Перетворенням симетрії (симетрією) відносно точки О називають таке перетворення фігури F у фігуру F′, внаслідок якого кожна точка Х фігури F переходить у точку Х′ фігури F′ , симетричну точці Х відносно точки О.
Симетрію відносно точки називають центральною симетрією.
Слайд #6
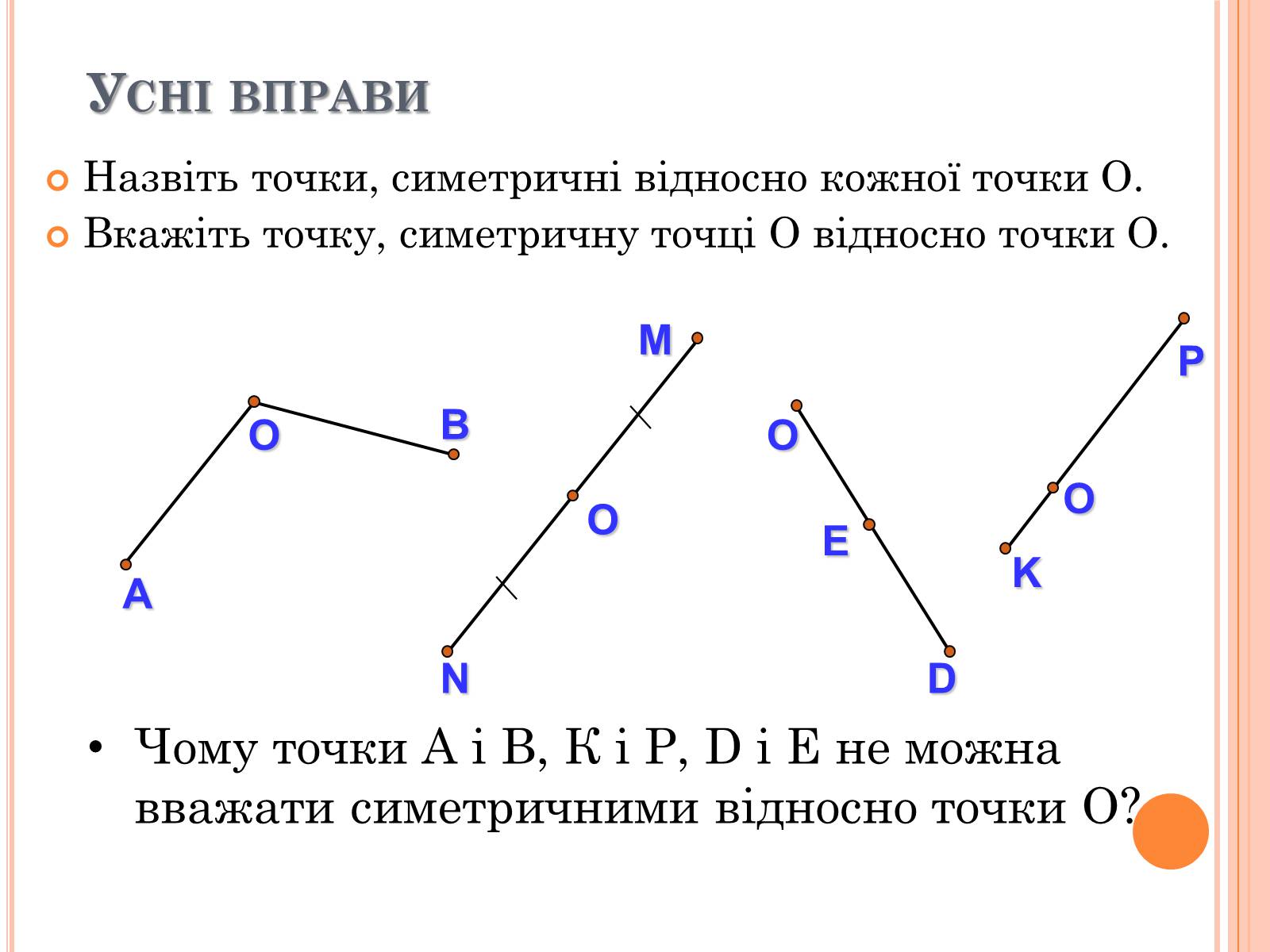
Усні вправи
Назвіть точки, симетричні відносно кожної точки О.
Вкажіть точку, симетричну точці О відносно точки О.
А
О
В
N
O
M
O
D
E
K
O
P
Чому точки А і В, К і Р, D і Е не можна вважати симетричними відносно точки О?
Назвіть точки, симетричні відносно кожної точки О.
Вкажіть точку, симетричну точці О відносно точки О.
А
О
В
N
O
M
O
D
E
K
O
P
Чому точки А і В, К і Р, D і Е не можна вважати симетричними відносно точки О?
Слайд #7
А1
А
О
Побудувати відрізок А1В1 симетричний відрізку АВ відносно точки О
Точка О –
центр симетрії
В
В1
Зауваження:
При центральній симетрії змінився порядок точок (згори-вниз, право-ліво).
Точка А відобразилась знизу вгору; вона була правіше від точки В, а її образ точка А1 виявилась лівіше точки В1.
А→А1, В → В1, АВ → А1В1
А
О
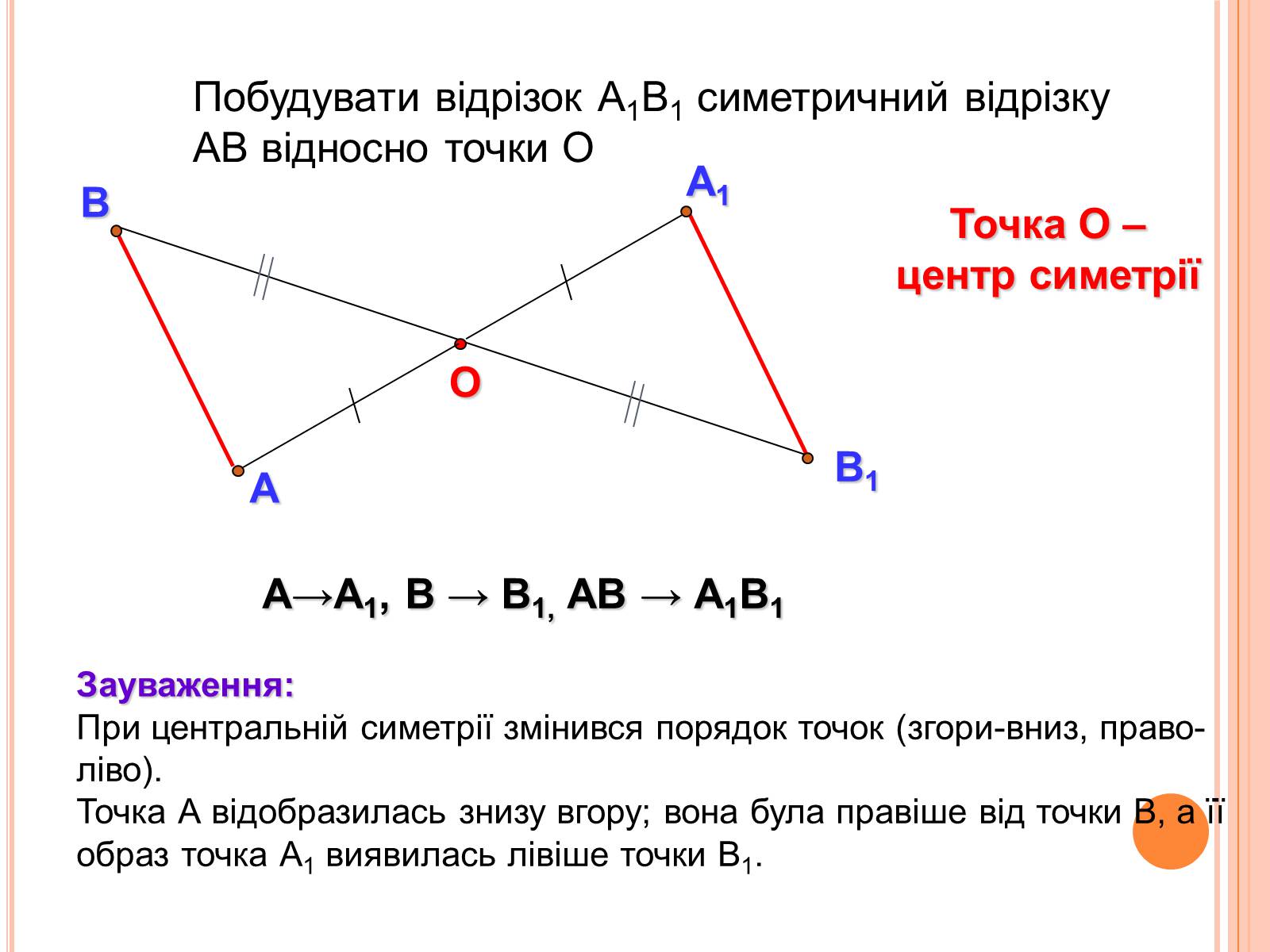
Побудувати відрізок А1В1 симетричний відрізку АВ відносно точки О
Точка О –
центр симетрії
В
В1
Зауваження:
При центральній симетрії змінився порядок точок (згори-вниз, право-ліво).
Точка А відобразилась знизу вгору; вона була правіше від точки В, а її образ точка А1 виявилась лівіше точки В1.
А→А1, В → В1, АВ → А1В1
Слайд #8
А1
О
Побудувати промінь, симетричний променю АВ відносно точки О
Точка О –
центр симетрії
В
В1
А
А→А1, В → В1, АВ → А1В1
О
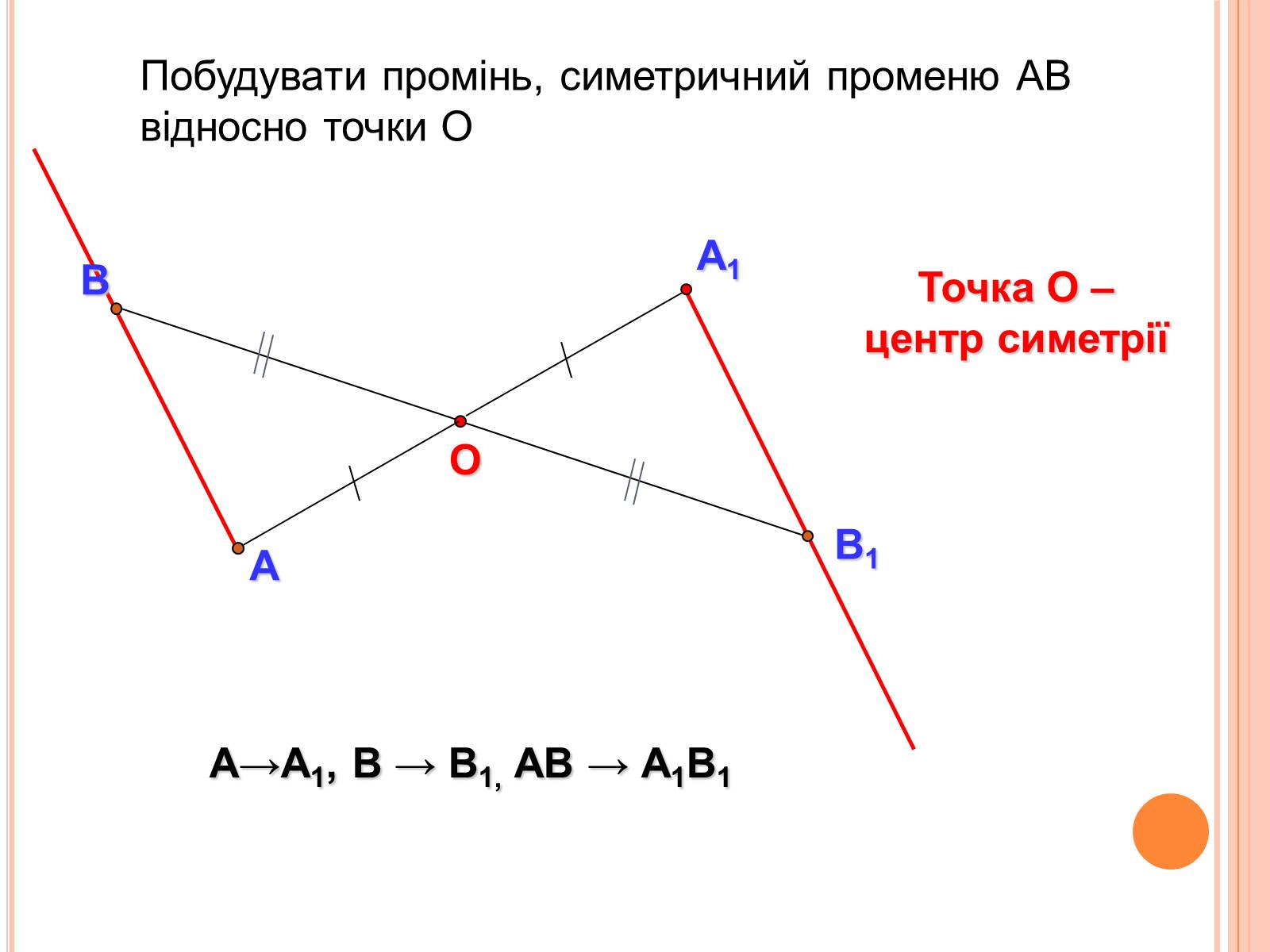
Побудувати промінь, симетричний променю АВ відносно точки О
Точка О –
центр симетрії
В
В1
А
А→А1, В → В1, АВ → А1В1
Слайд #9
О
А
В
В1
С
С1
А1
Зауваження.
Якщо центр симетрії міститься поза фігурою, то фігура і її образ не мають спільних точок.
Побудувати трикутник, симетричний трикутнику АВС відносно точки О
А→А1,
С→С1,
В→В1,
∆АВС→∆А1В1С1
А
В
В1
С
С1
А1
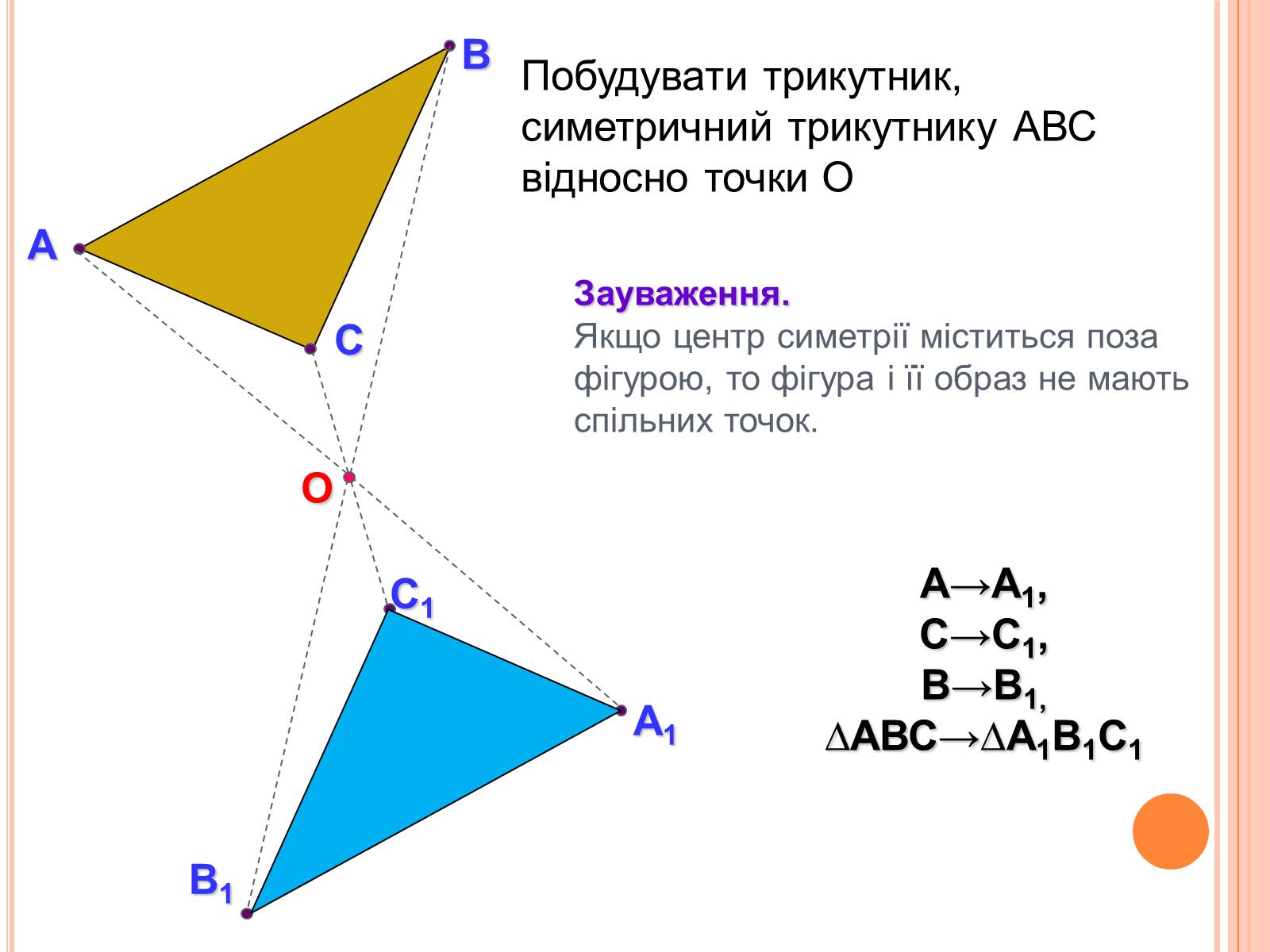
Зауваження.
Якщо центр симетрії міститься поза фігурою, то фігура і її образ не мають спільних точок.
Побудувати трикутник, симетричний трикутнику АВС відносно точки О
А→А1,
С→С1,
В→В1,
∆АВС→∆А1В1С1
Слайд #10
А
В
Зауваження.
Якщо центр симетрії – одна з вершин фігури, то фігура і її образ мають спільну точку (точка С).
А1
В1
С
О
Побудова трикутника, симетричного трикутнику АВС відносно точки С
А→А1,
С→С1,
В→В1,
∆АВС→∆А1В1С1
В
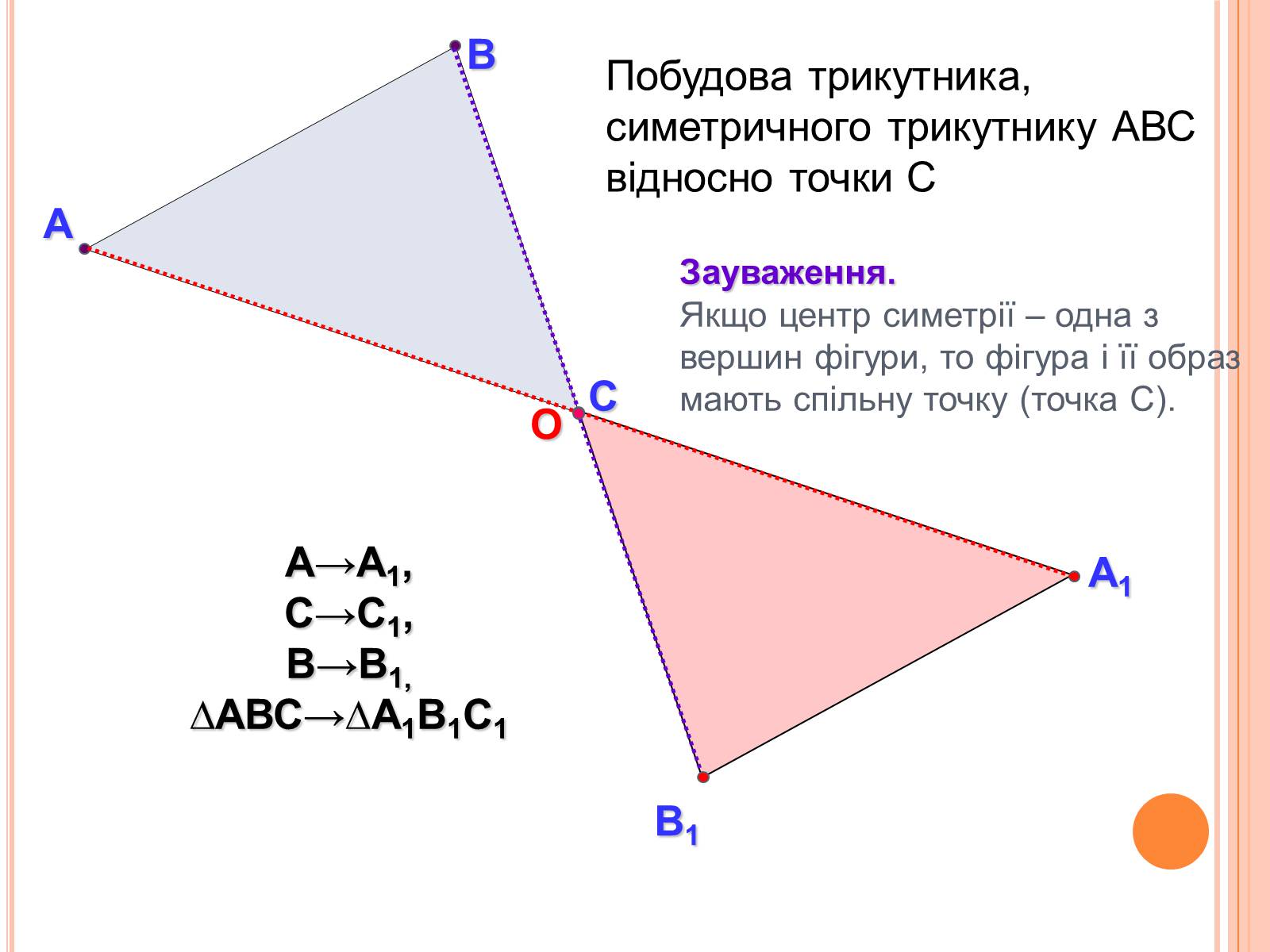
Зауваження.
Якщо центр симетрії – одна з вершин фігури, то фігура і її образ мають спільну точку (точка С).
А1
В1
С
О
Побудова трикутника, симетричного трикутнику АВС відносно точки С
А→А1,
С→С1,
В→В1,
∆АВС→∆А1В1С1
Слайд #11
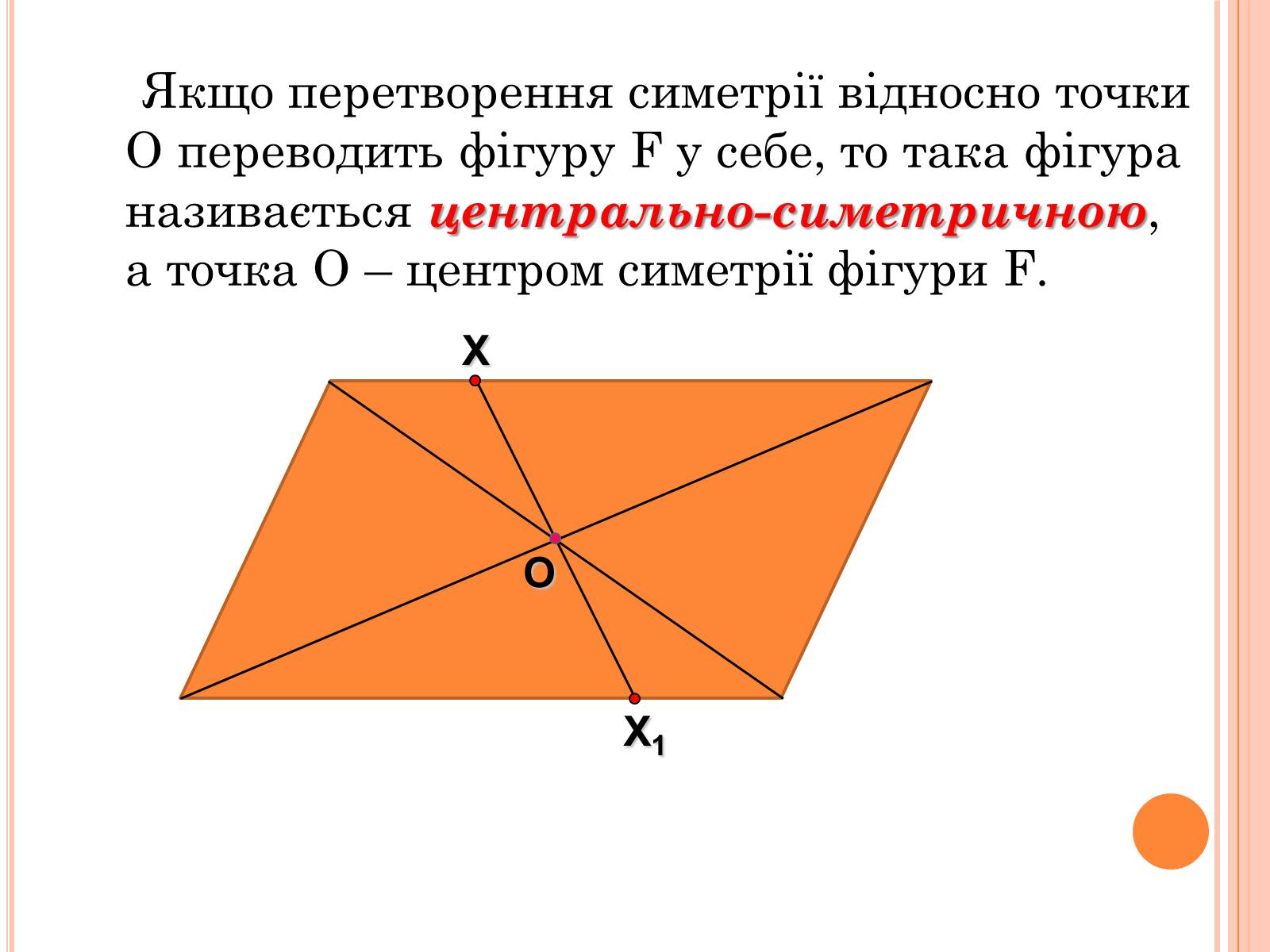
Якщо перетворення симетрії відносно точки О переводить фігуру F у себе, то така фігура називається центрально-симетричною, а точка О – центром симетрії фігури F.
Х1
О
Х
Х1
О
Х
Слайд #12
Х1
Х
О
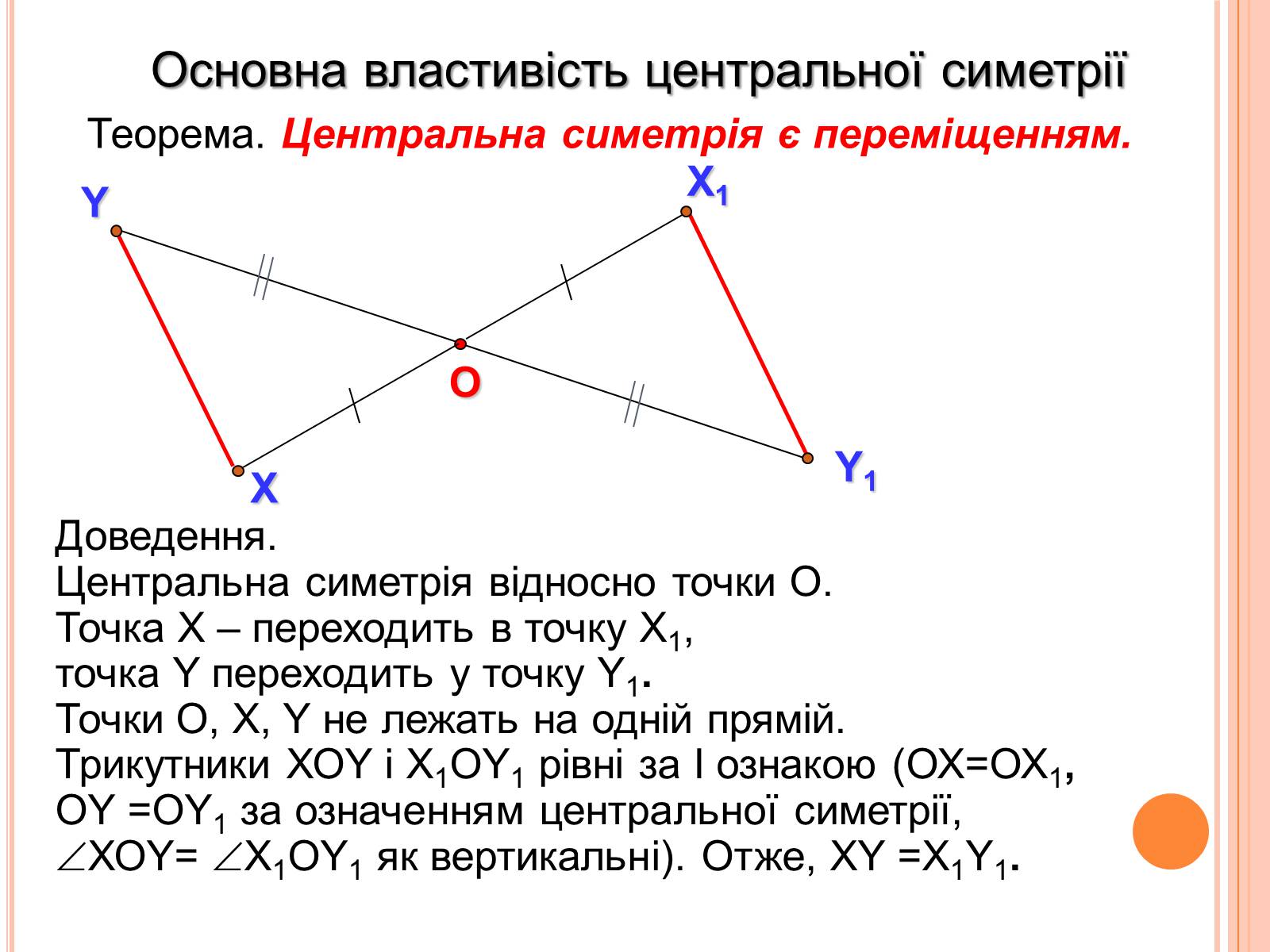
Основна властивість центральної симетрії
Теорема. Центральна симетрія є переміщенням.
Y
Y1
Доведення.
Центральна симетрія відносно точки О.
Точка Х – переходить в точку Х1,
точка Y переходить у точку Y1.
Точки О, Х, Y не лежать на одній прямій.
Трикутники ХОY і Х1ОY1 рівні за І ознакою (ОХ=ОХ1,
ОY =ОY1 за означенням центральної симетрії,
ХОY= Х1ОY1 як вертикальні). Отже, ХY =Х1Y1.
Х
О
Основна властивість центральної симетрії
Теорема. Центральна симетрія є переміщенням.
Y
Y1
Доведення.
Центральна симетрія відносно точки О.
Точка Х – переходить в точку Х1,
точка Y переходить у точку Y1.
Точки О, Х, Y не лежать на одній прямій.
Трикутники ХОY і Х1ОY1 рівні за І ознакою (ОХ=ОХ1,
ОY =ОY1 за означенням центральної симетрії,
ХОY= Х1ОY1 як вертикальні). Отже, ХY =Х1Y1.
Слайд #13
Властивості симетрії відносно точки
Перетворення симетрії відносно точки є переміщенням.
Перетворення симетрії відносно точки перетворює пряму на паралельну їй пряму або на себе; відрізок – на рівний і паралельний йому відрізок; многокутник – на рівний йому многокутник.
Будь-яка пряма, що проходить через центр симетрії, відображається при цій симетрії на себе.
Якщо точка А(х;у) симетрична точці В(х1; у1) відносно початку координат О, то виконуються умови: х1=-х, у1=-у.
Перетворення симетрії відносно точки є переміщенням.
Перетворення симетрії відносно точки перетворює пряму на паралельну їй пряму або на себе; відрізок – на рівний і паралельний йому відрізок; многокутник – на рівний йому многокутник.
Будь-яка пряма, що проходить через центр симетрії, відображається при цій симетрії на себе.
Якщо точка А(х;у) симетрична точці В(х1; у1) відносно початку координат О, то виконуються умови: х1=-х, у1=-у.

Слайд #14
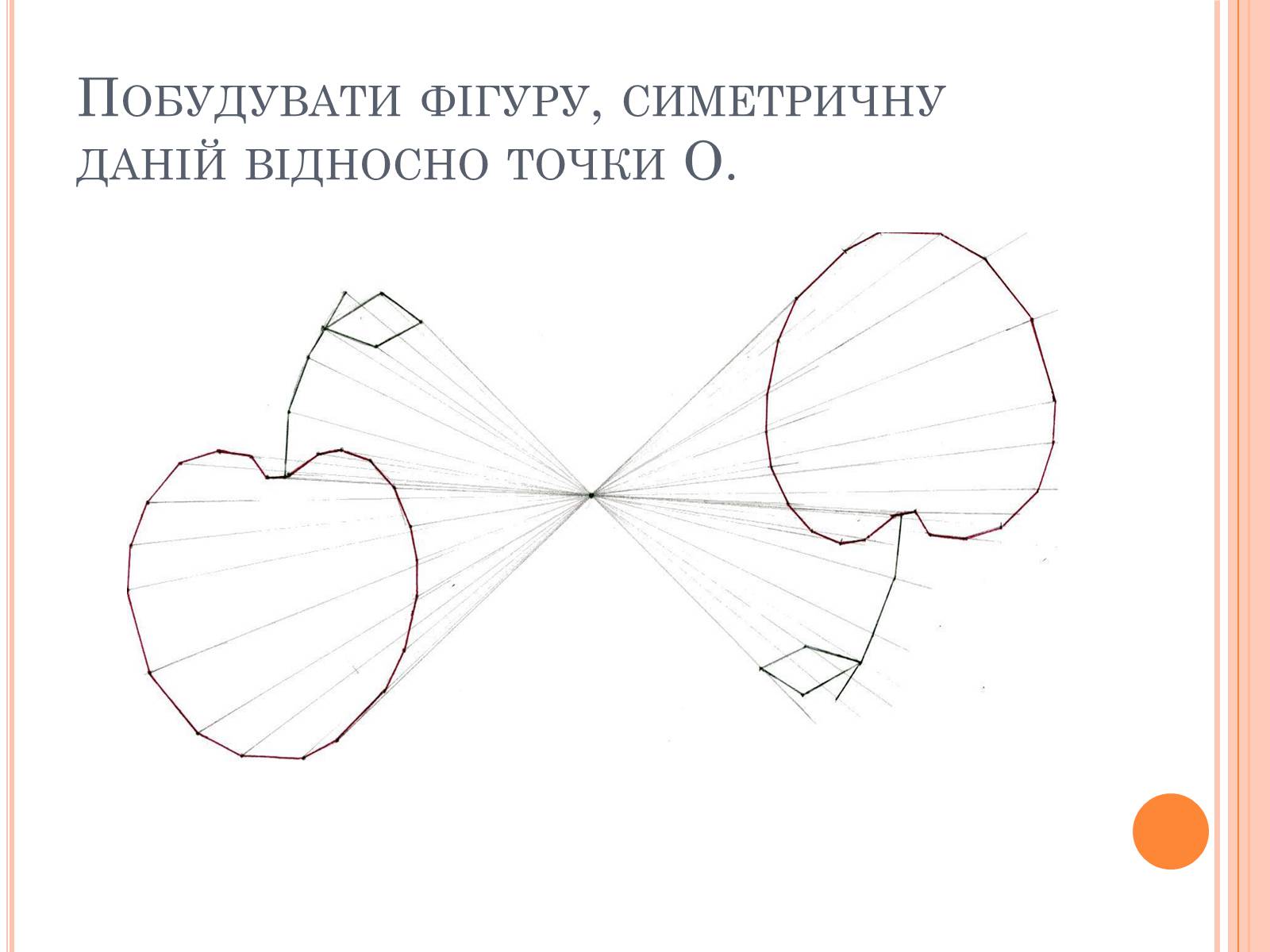
Побудувати фігуру, симетричну даній відносно точки О.
Слайд #15
Центральна симетрія в природі