- Головна
- Готові шкільні презентації
- Презентація на тему «Теорема про три перпендикуляри»
Презентація на тему «Теорема про три перпендикуляри»
1144
Слайд #1
Геометрія
Теорема про три перпендикуляри
Робота
учениці 10-А класу
Баранюк Надії
Теорема про три перпендикуляри
Робота
учениці 10-А класу
Баранюк Надії

Слайд #2
Відрізок АВ - перпендикуляр, точка В — основа цього перпендикуляра.
Будь-який відрізок АС, де С — довільна точка площини α, відмінна від В, називається похилою до цієї площини.
Узагальнююче повторення
Перпендикуляр і похила
Будь-який відрізок АС, де С — довільна точка площини α, відмінна від В, називається похилою до цієї площини.
Узагальнююче повторення
Перпендикуляр і похила

Слайд #3
Властивості проекції
1. Перпендикуляр, проведений з даної точки до площини, менший будь-якої похилої, проведеної з тієї ж точки доцієї площини.
2. Якщо похилі рівні, то рівні і їх проекції;
3. Якщо проекції похилих рівні, то рівні і похилі;
4. Якщо похилі не рівні, то більша похила має і більшу проекцію.
1. Перпендикуляр, проведений з даної точки до площини, менший будь-якої похилої, проведеної з тієї ж точки доцієї площини.
2. Якщо похилі рівні, то рівні і їх проекції;
3. Якщо проекції похилих рівні, то рівні і похилі;
4. Якщо похилі не рівні, то більша похила має і більшу проекцію.

Слайд #4
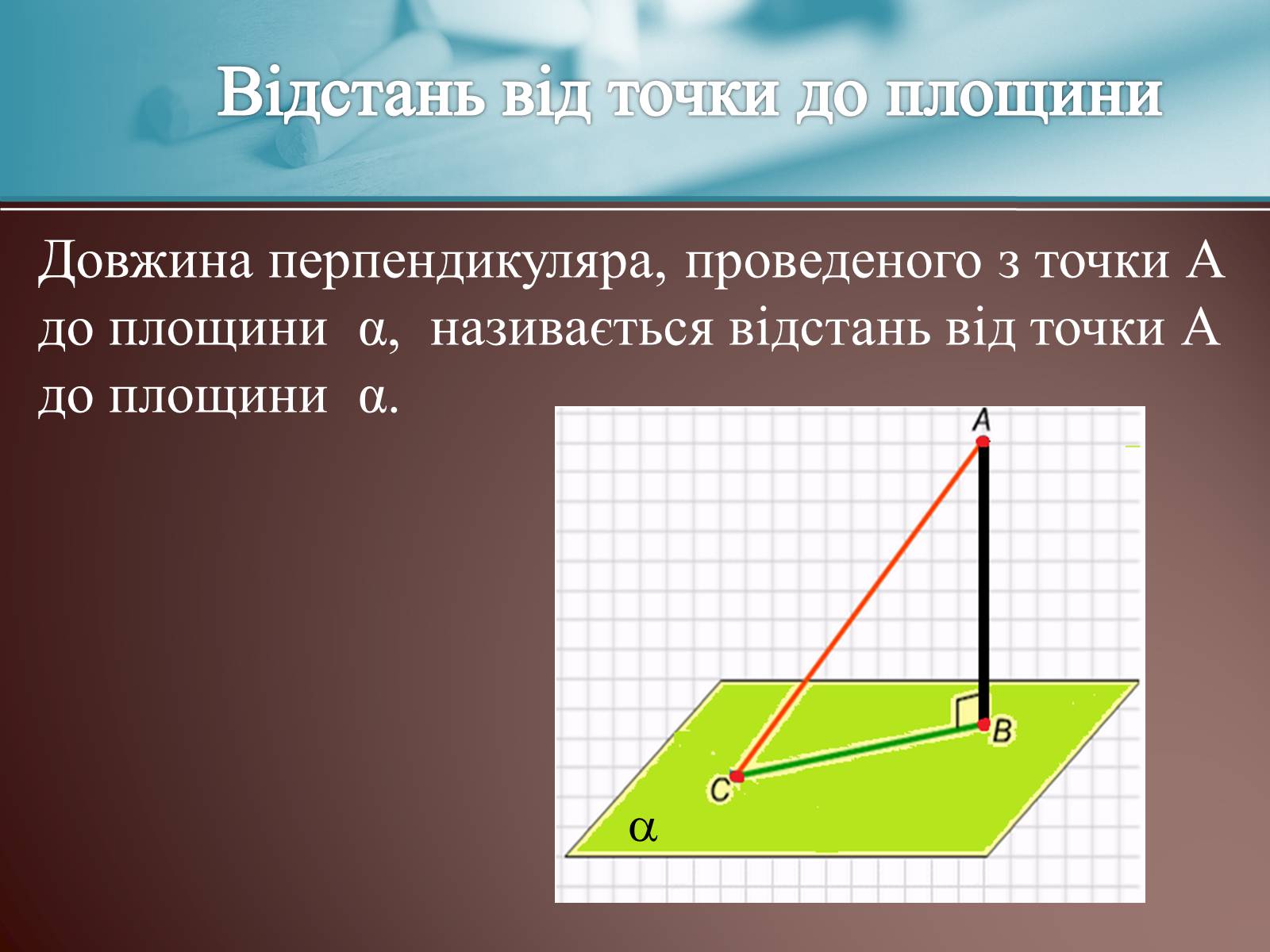
Відстань від точки до площини
Довжина перпендикуляра, проведеного з точки А до площини α, називається відстань від точки А до площини α.
Довжина перпендикуляра, проведеного з точки А до площини α, називається відстань від точки А до площини α.
Слайд #5
α
a
A
b
c
d
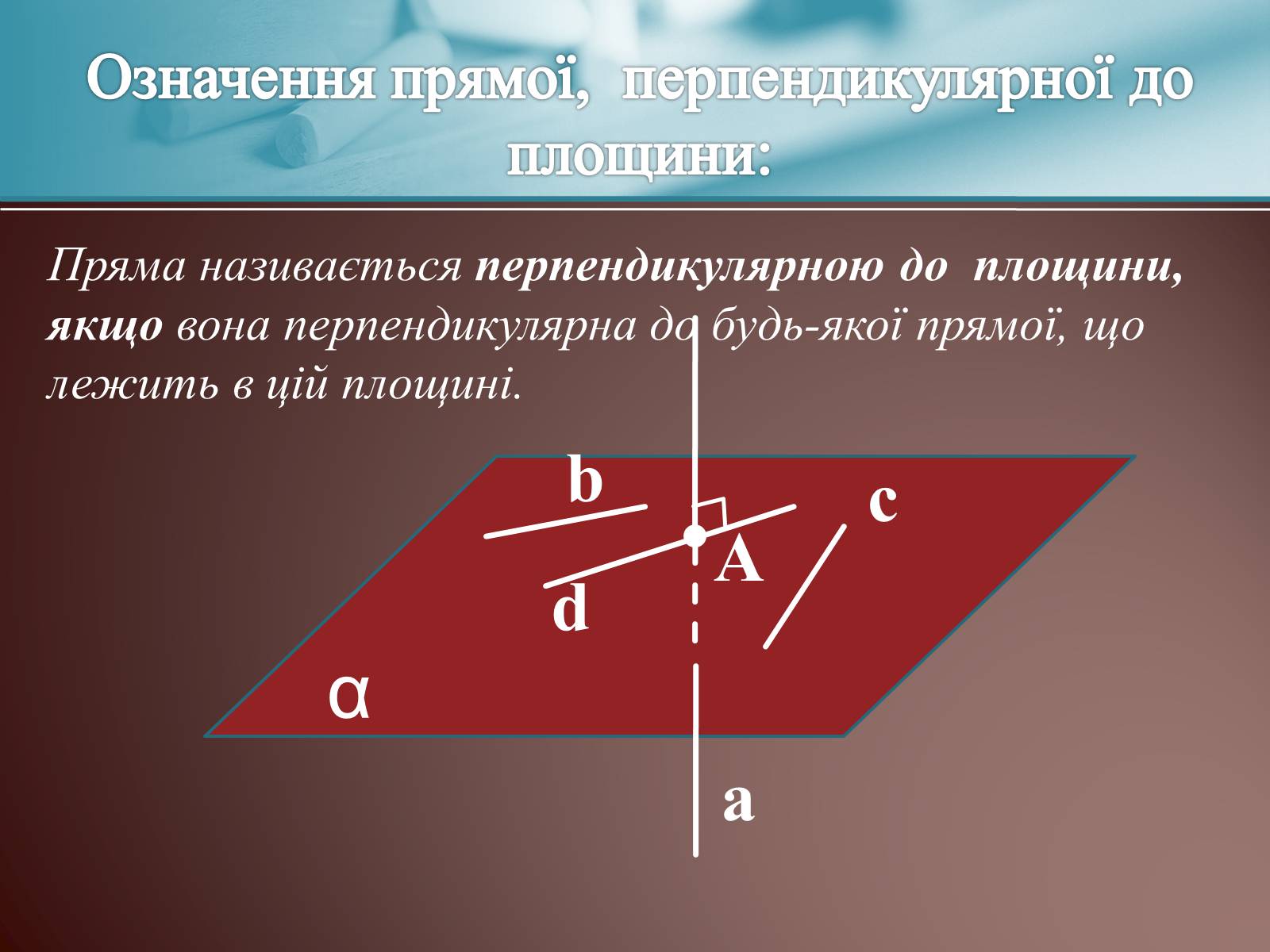
Означення прямої, перпендикулярної до площини:
Пряма називається перпендикулярною до площини, якщо вона перпендикулярна до будь-якої прямої, що лежить в цій площині.
a
A
b
c
d
Означення прямої, перпендикулярної до площини:
Пряма називається перпендикулярною до площини, якщо вона перпендикулярна до будь-якої прямої, що лежить в цій площині.
Слайд #6
α
a
A
b
c
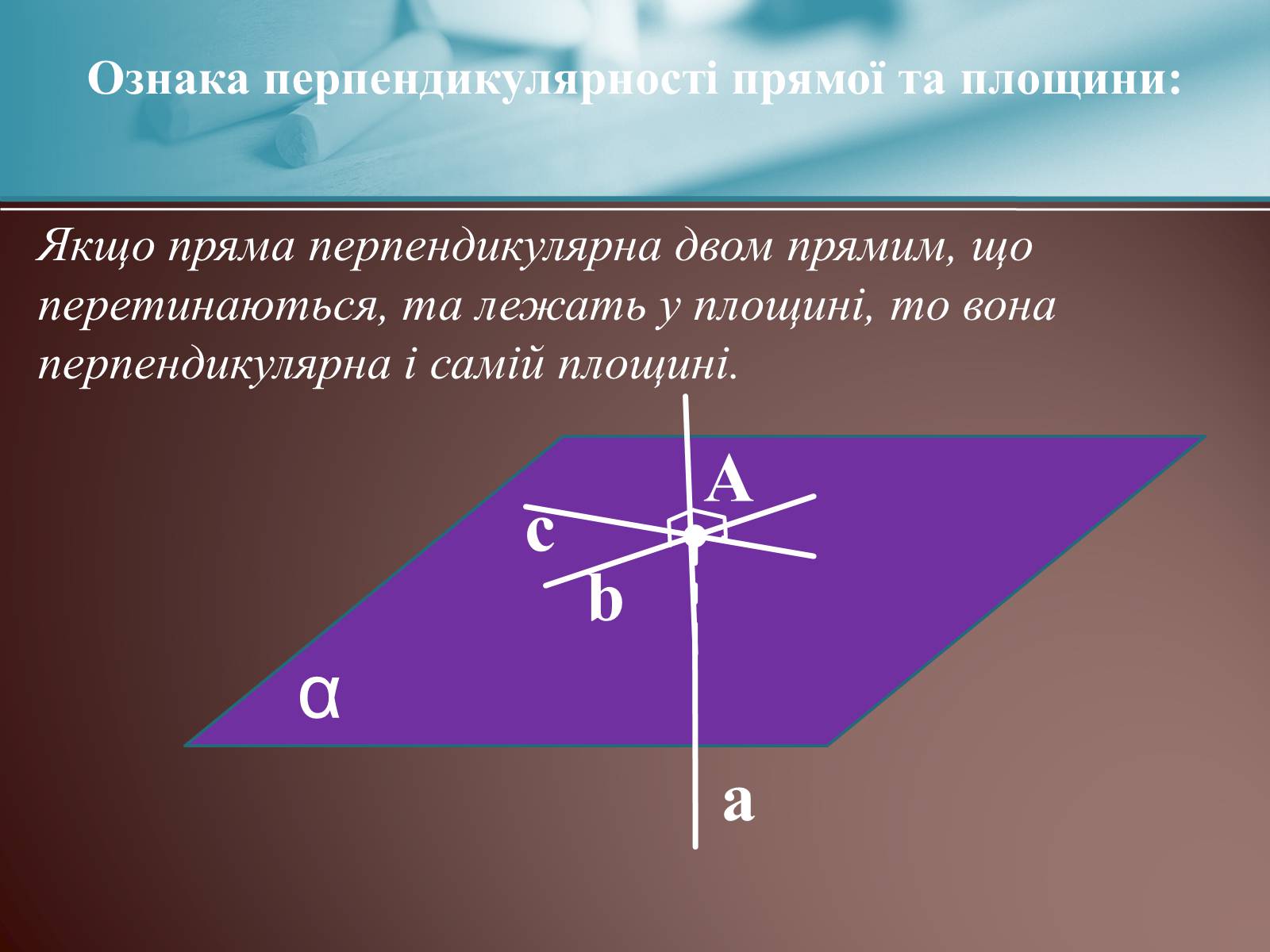
Якщо пряма перпендикулярна двом прямим, що перетинаються, та лежать у площині, то вона
перпендикулярна і самій площині.
Ознака перпендикулярності прямої та площини:
a
A
b
c
Якщо пряма перпендикулярна двом прямим, що перетинаються, та лежать у площині, то вона
перпендикулярна і самій площині.
Ознака перпендикулярності прямої та площини:
Слайд #7
α
A
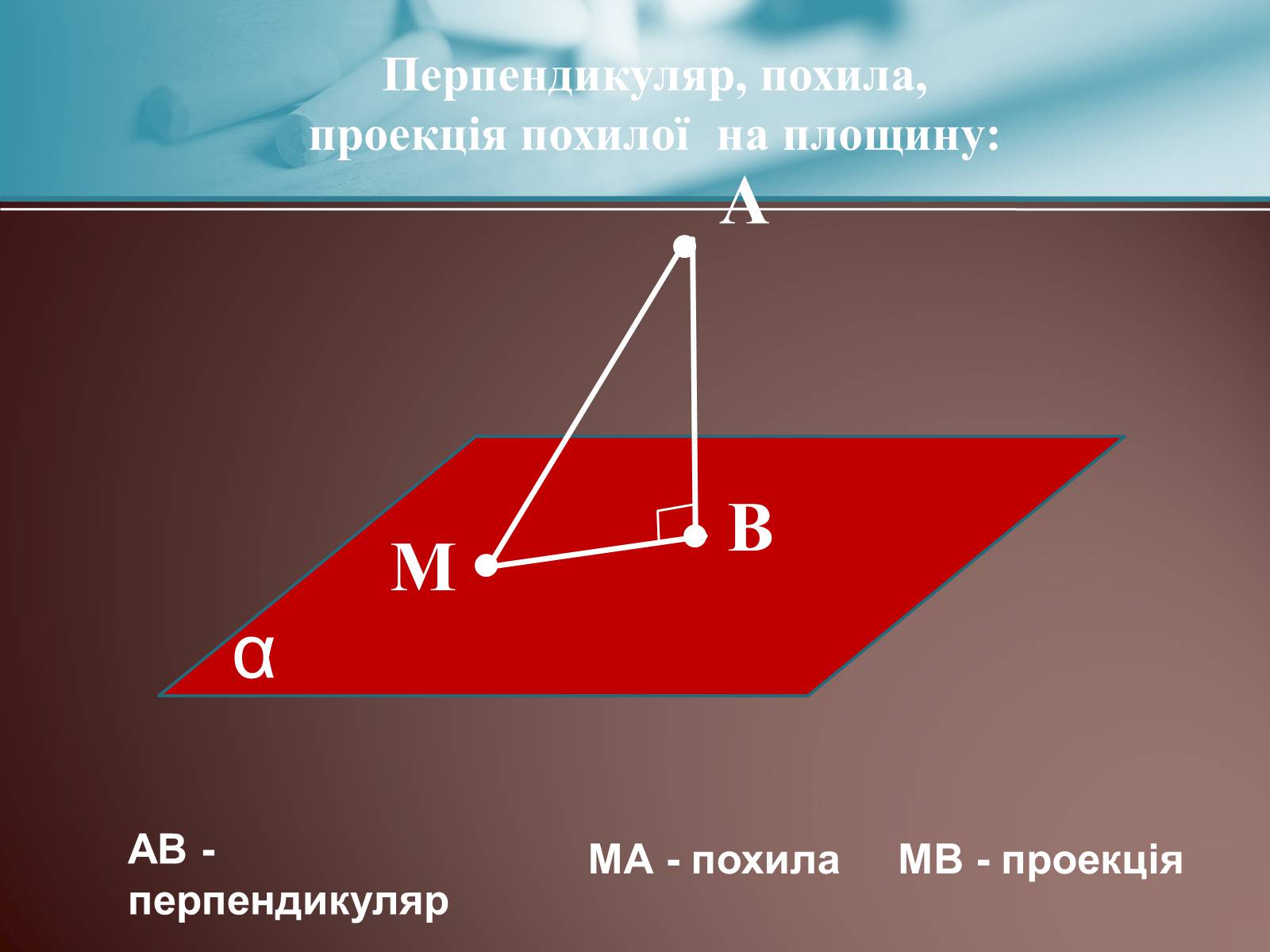
Перпендикуляр, похила,
проекція похилої на площину:
В
М
АВ - перпендикуляр
МА - похила
МВ - проекція
A
Перпендикуляр, похила,
проекція похилої на площину:
В
М
АВ - перпендикуляр
МА - похила
МВ - проекція
Слайд #8
М
α
А
В
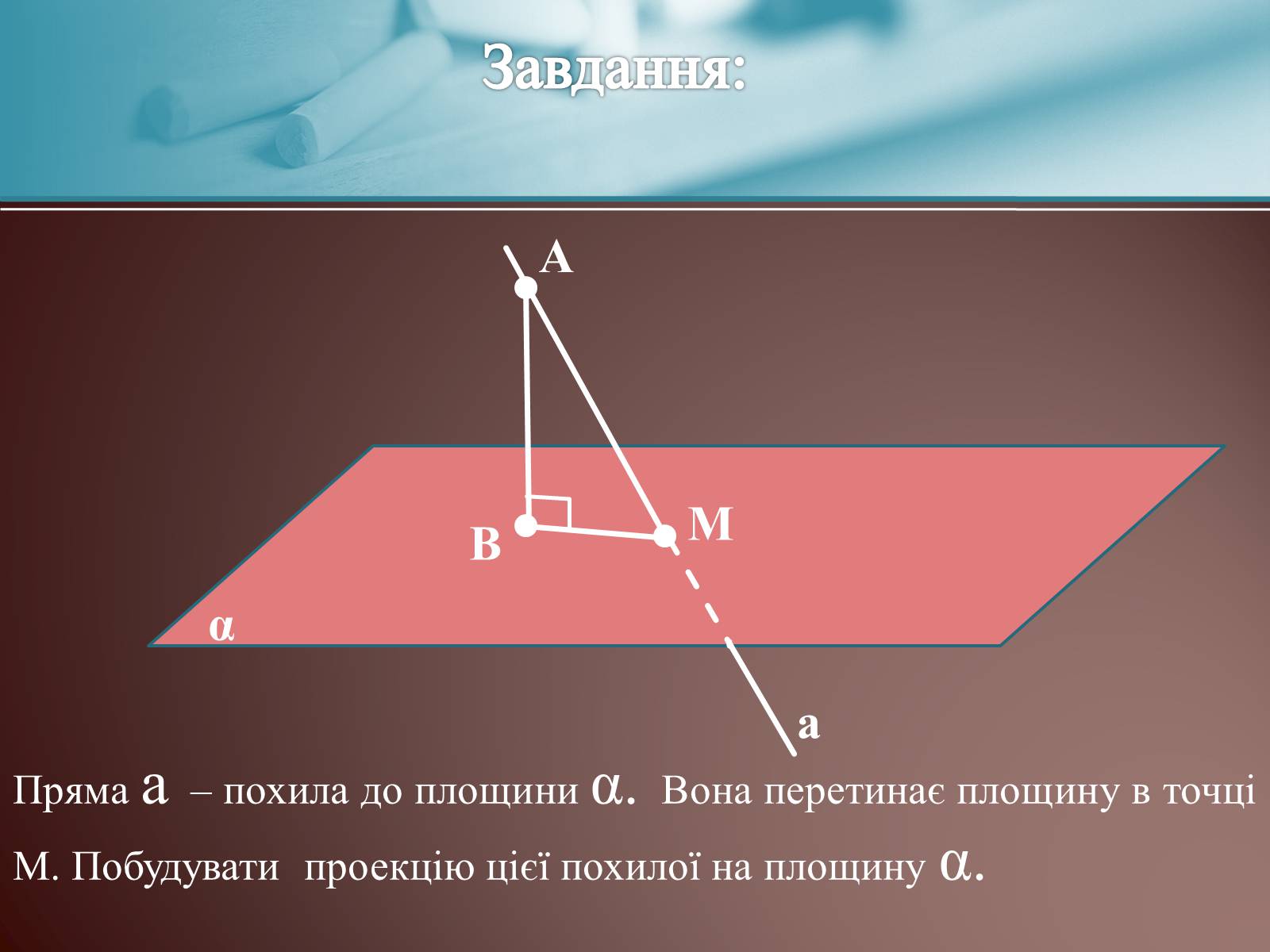
Завдання:
а
Пряма a – похила до площини α. Вона перетинає площину в точці М. Побудувати проекцію цієї похилої на площину α.
α
А
В
Завдання:
а
Пряма a – похила до площини α. Вона перетинає площину в точці М. Побудувати проекцію цієї похилої на площину α.
Слайд #9
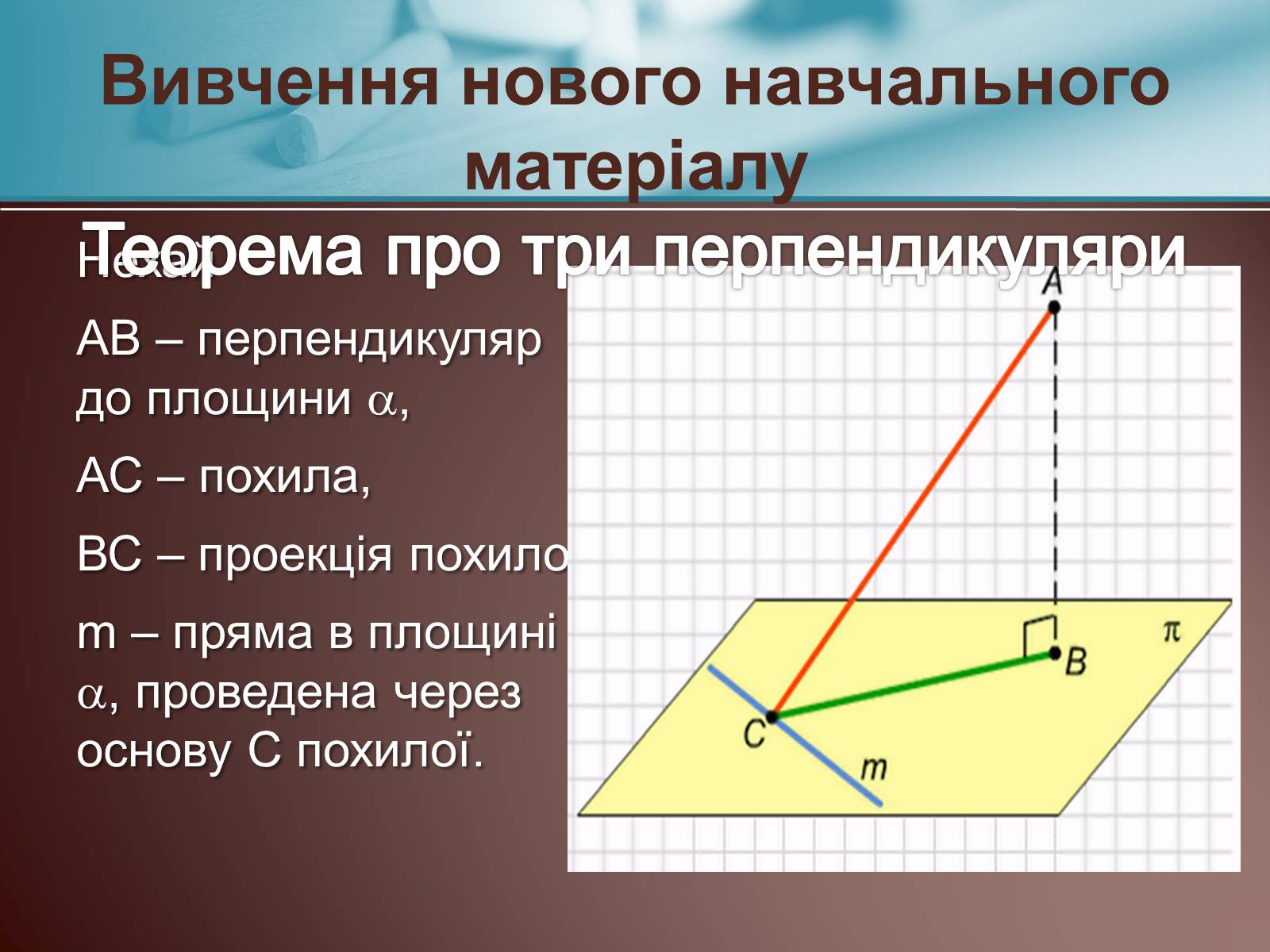
Нехай
АВ – перпендикуляр до площини ,
АС – похила,
ВС – проекція похилої
m – пряма в площині , проведена через основу С похилої.
Вивчення нового навчального матеріалу
Теорема про три перпендикуляри
АВ – перпендикуляр до площини ,
АС – похила,
ВС – проекція похилої
m – пряма в площині , проведена через основу С похилої.
Вивчення нового навчального матеріалу
Теорема про три перпендикуляри
Слайд #10
α
A
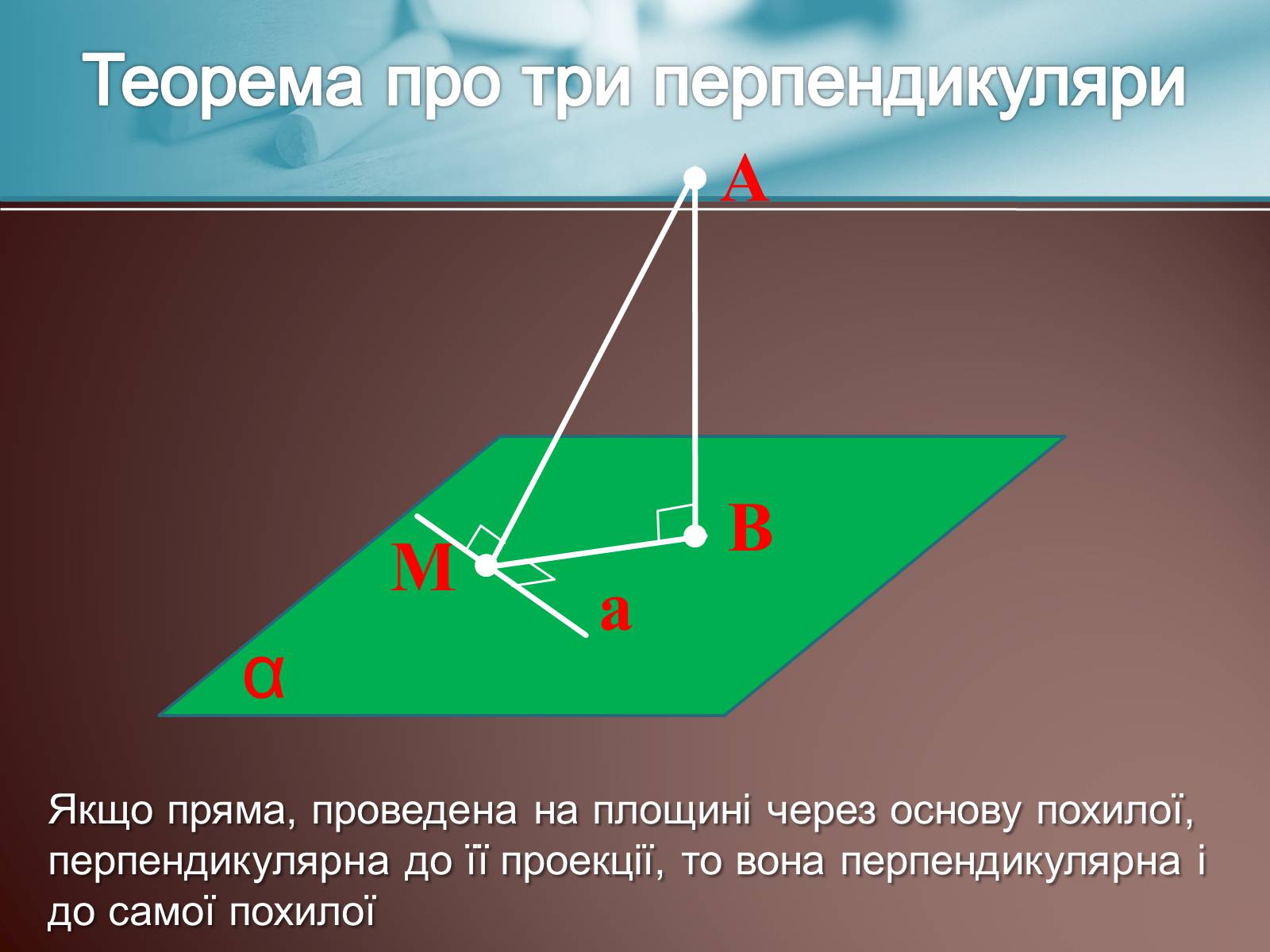
Теорема про три перпендикуляри
В
М
а
Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна і до самої похилої
A
Теорема про три перпендикуляри
В
М
а
Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна і до самої похилої
Слайд #11
α
A
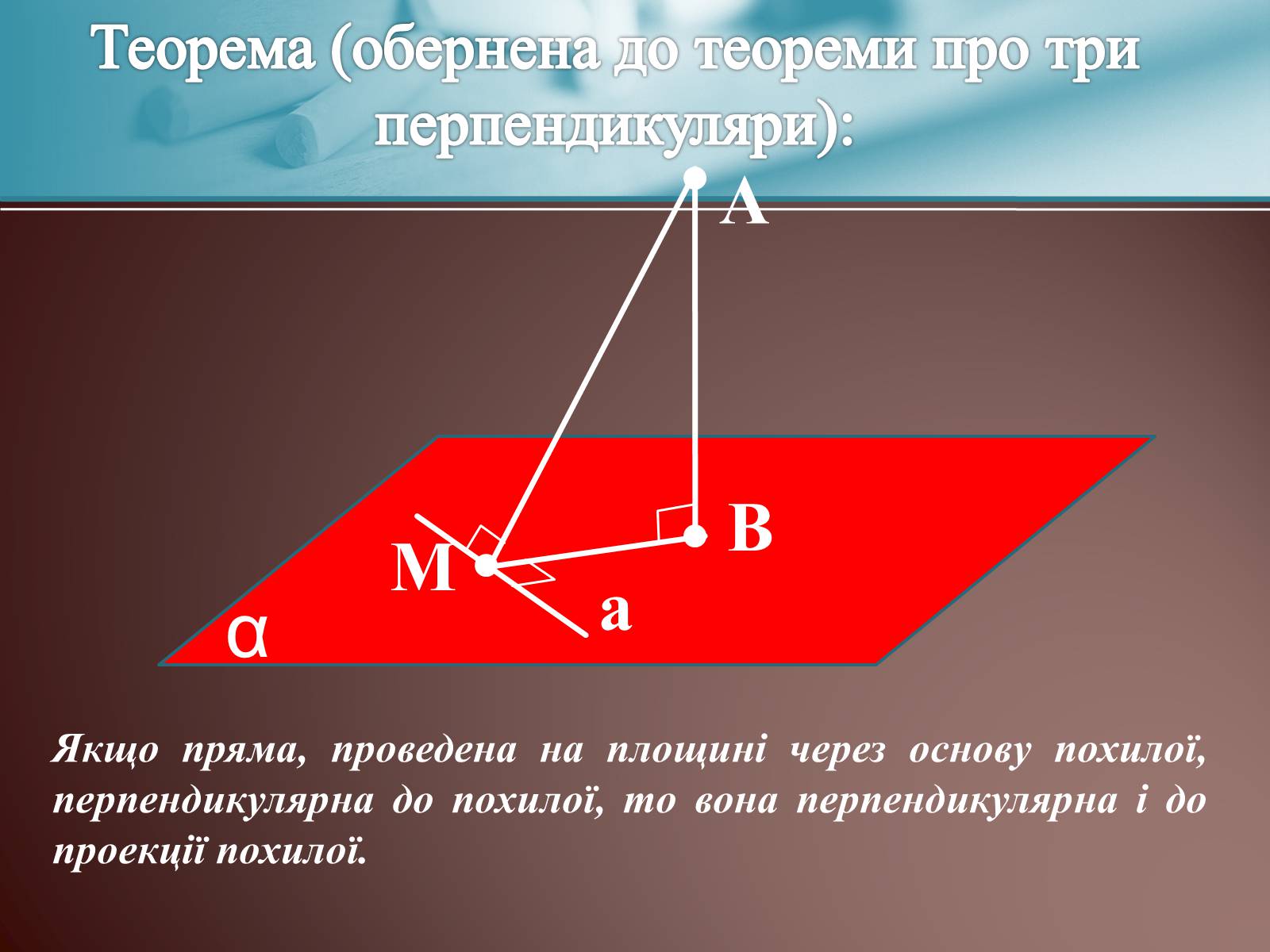
Теорема (обернена до теореми про три перпендикуляри):
В
М
а
Якщо пряма, проведена на площині через основу похилої, перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.
A
Теорема (обернена до теореми про три перпендикуляри):
В
М
а
Якщо пряма, проведена на площині через основу похилої, перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.
Слайд #12
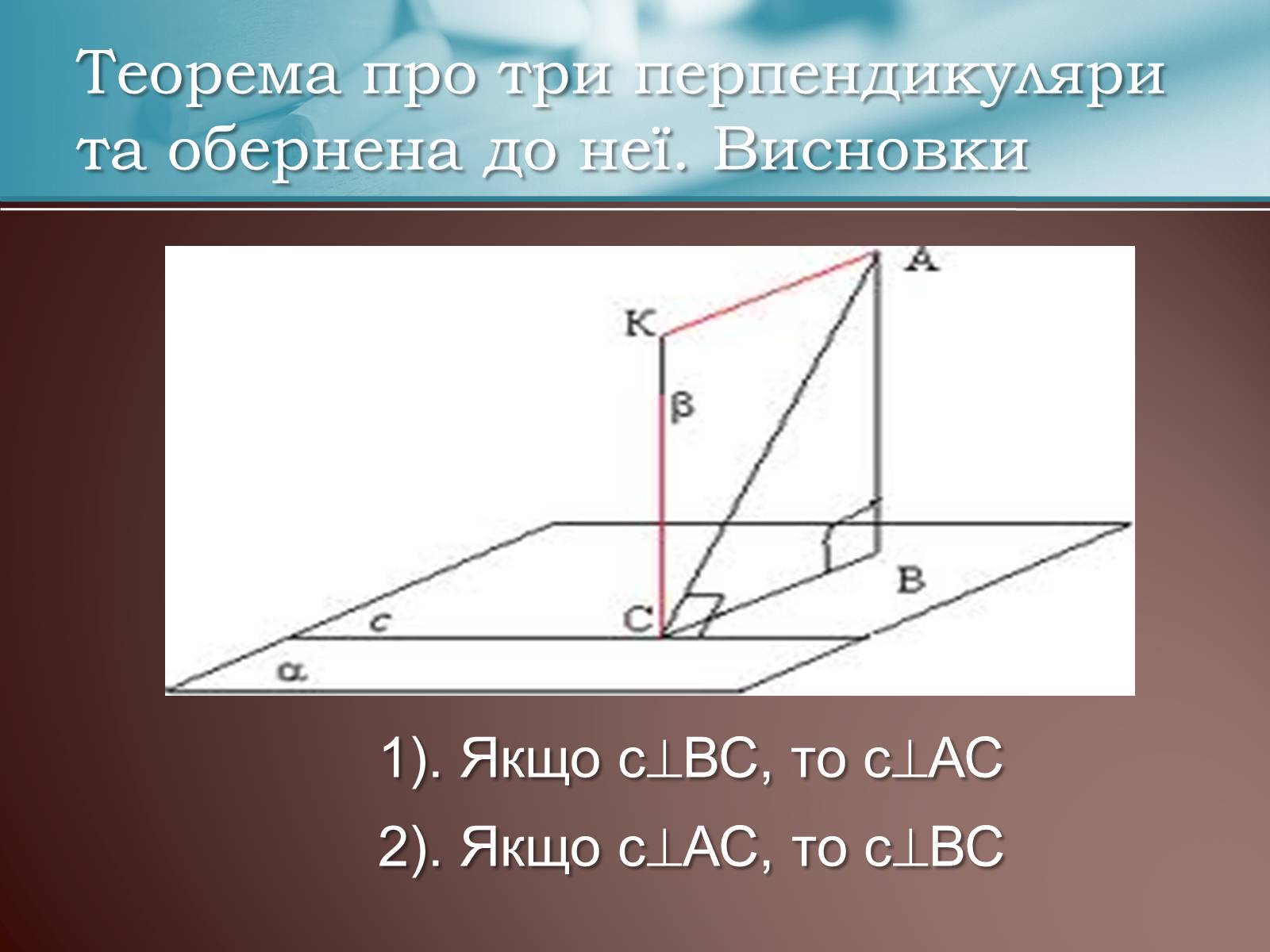
Теорема про три перпендикуляри та обернена до неї. Висновки
1). Якщо сВС, то сАС
2). Якщо сАС, то сВС
1). Якщо сВС, то сАС
2). Якщо сАС, то сВС
Слайд #13
Первинне закріплення вивченого матеріалу
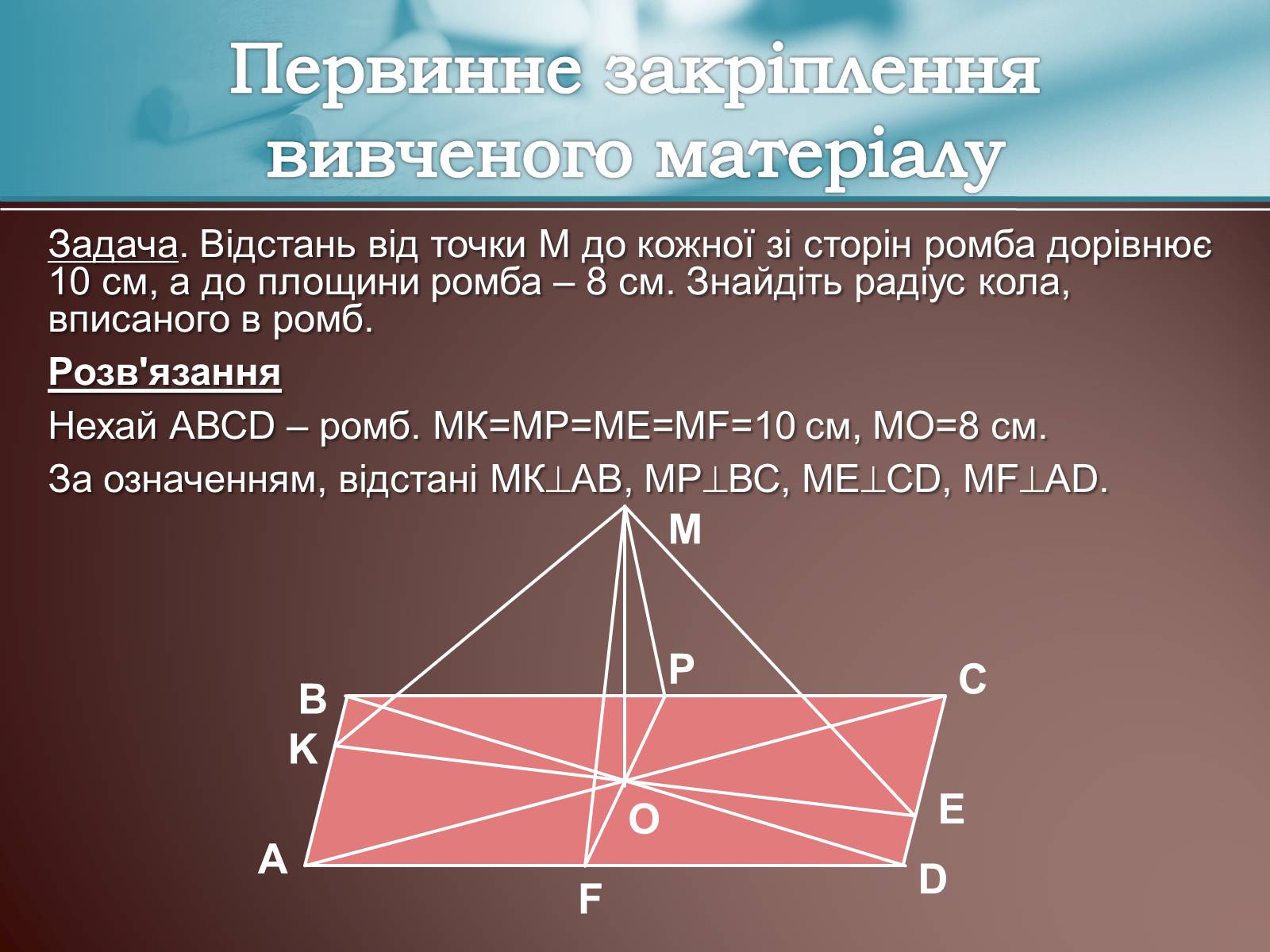
Задача. Відстань від точки М до кожної зі сторін ромба дорівнює 10 см, а до площини ромба – 8 см. Знайдіть радіус кола, вписаного в ромб.
Розв'язання
Нехай АВСD – ромб. МК=МР=МЕ=MF=10 см, МО=8 см.
За означенням, відстані МКАВ, МРВС, МЕCD, MFAD.
K
E
P
M
D
С
В
А
F
O
Задача. Відстань від точки М до кожної зі сторін ромба дорівнює 10 см, а до площини ромба – 8 см. Знайдіть радіус кола, вписаного в ромб.
Розв'язання
Нехай АВСD – ромб. МК=МР=МЕ=MF=10 см, МО=8 см.
За означенням, відстані МКАВ, МРВС, МЕCD, MFAD.
K
E
P
M
D
С
В
А
F
O
Слайд #14
Первинне закріплення вивченого матеріалу
За теоремою про три перпендикуляри ОКАВ, ОР ВС, ОЕ CD, OF AD.
Оскільки відстані від точки М до сторін ромба рівні, то відрізки ОК, ОР, ОЕ, OF також рівні як проекції рівних похилих. Звідси точка О - основа перпендикуляра МО – є центром кола, вписаного в ромб. Із прямокутного трикутника МОК знайдемо радіус цього кола:
За теоремою про три перпендикуляри ОКАВ, ОР ВС, ОЕ CD, OF AD.
Оскільки відстані від точки М до сторін ромба рівні, то відрізки ОК, ОР, ОЕ, OF також рівні як проекції рівних похилих. Звідси точка О - основа перпендикуляра МО – є центром кола, вписаного в ромб. Із прямокутного трикутника МОК знайдемо радіус цього кола:

Слайд #15
Висновок 1
Якщо т. А однаково віддалена від усіх сторін многокутника, то основа перпендикуляра, проведеного з цієї точки до площини многокутника, також однаково віддалена від його сторін, тобто є центром вписаного в многокутник кола.
Якщо т. А однаково віддалена від усіх сторін многокутника, то основа перпендикуляра, проведеного з цієї точки до площини многокутника, також однаково віддалена від його сторін, тобто є центром вписаного в многокутник кола.

Слайд #16
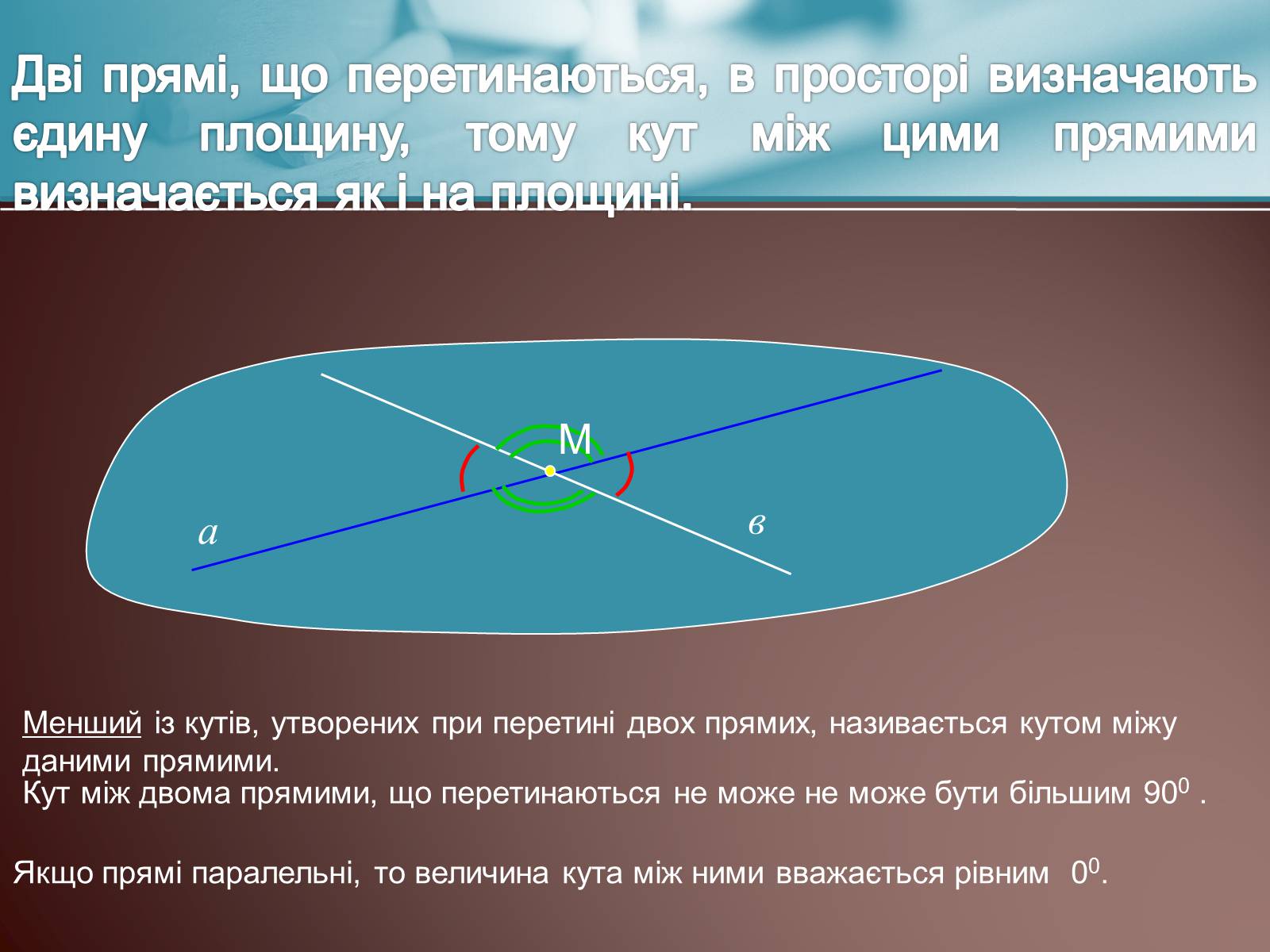
Дві прямі, що перетинаються, в просторі визначають єдину площину, тому кут між цими прямими визначається як і на площині.
а
в
Менший із кутів, утворених при перетині двох прямих, називається кутом міжу даними прямими.
Кут між двома прямими, що перетинаються не може не може бути більшим 900 .
Якщо прямі паралельні, то величина кута між ними вважається рівним 00.
М
а
в
Менший із кутів, утворених при перетині двох прямих, називається кутом міжу даними прямими.
Кут між двома прямими, що перетинаються не може не може бути більшим 900 .
Якщо прямі паралельні, то величина кута між ними вважається рівним 00.
М
Слайд #17
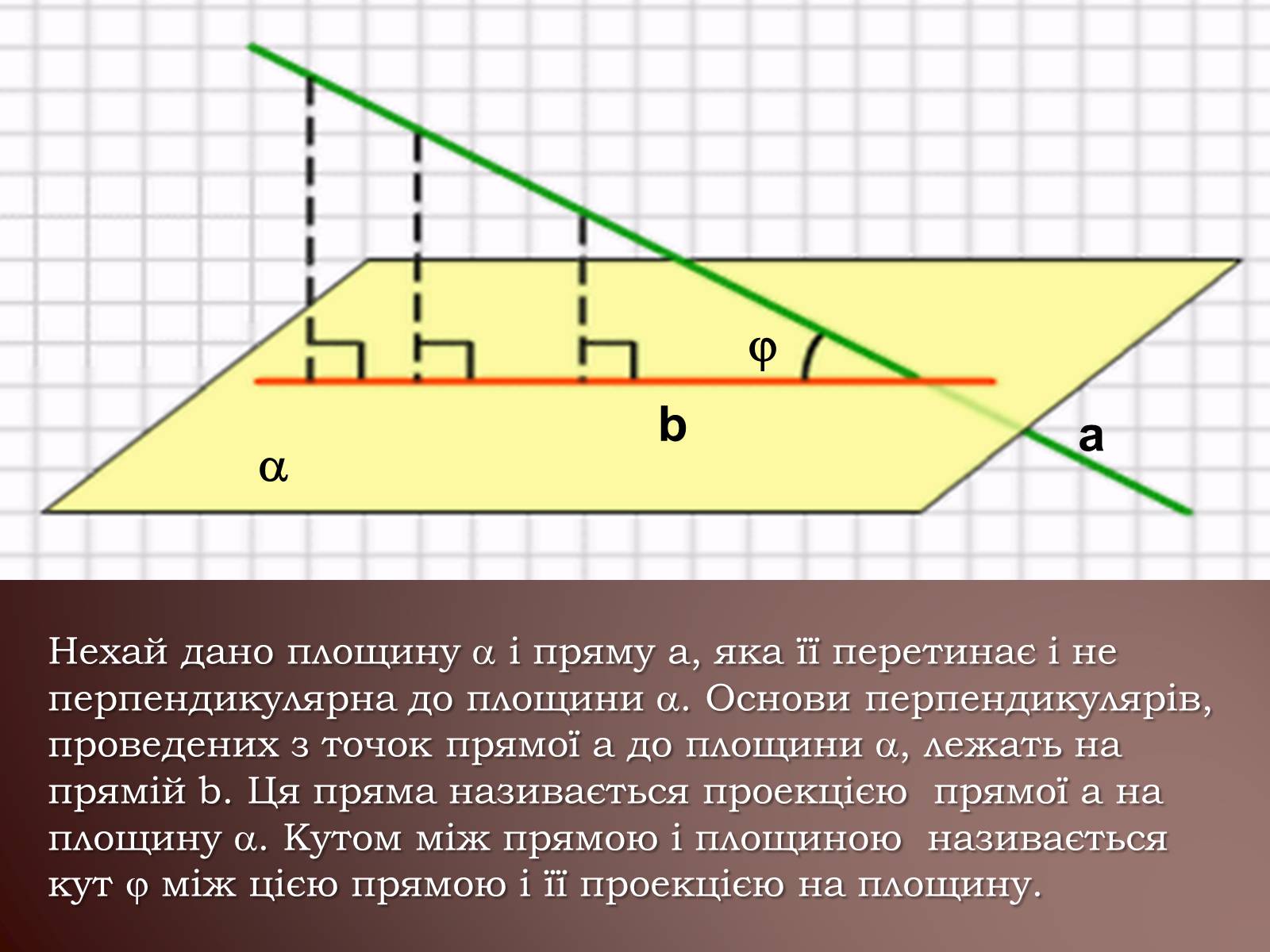
Нехай дано площину і пряму а, яка її перетинає і не перпендикулярна до площини . Основи перпендикулярів, проведених з точок прямої а до площини , лежать на прямій b. Ця пряма називається проекцією прямої а на площину . Кутом між прямою і площиною називається кут між цією прямою і її проекцією на площину.
b
а
b
а
Слайд #18
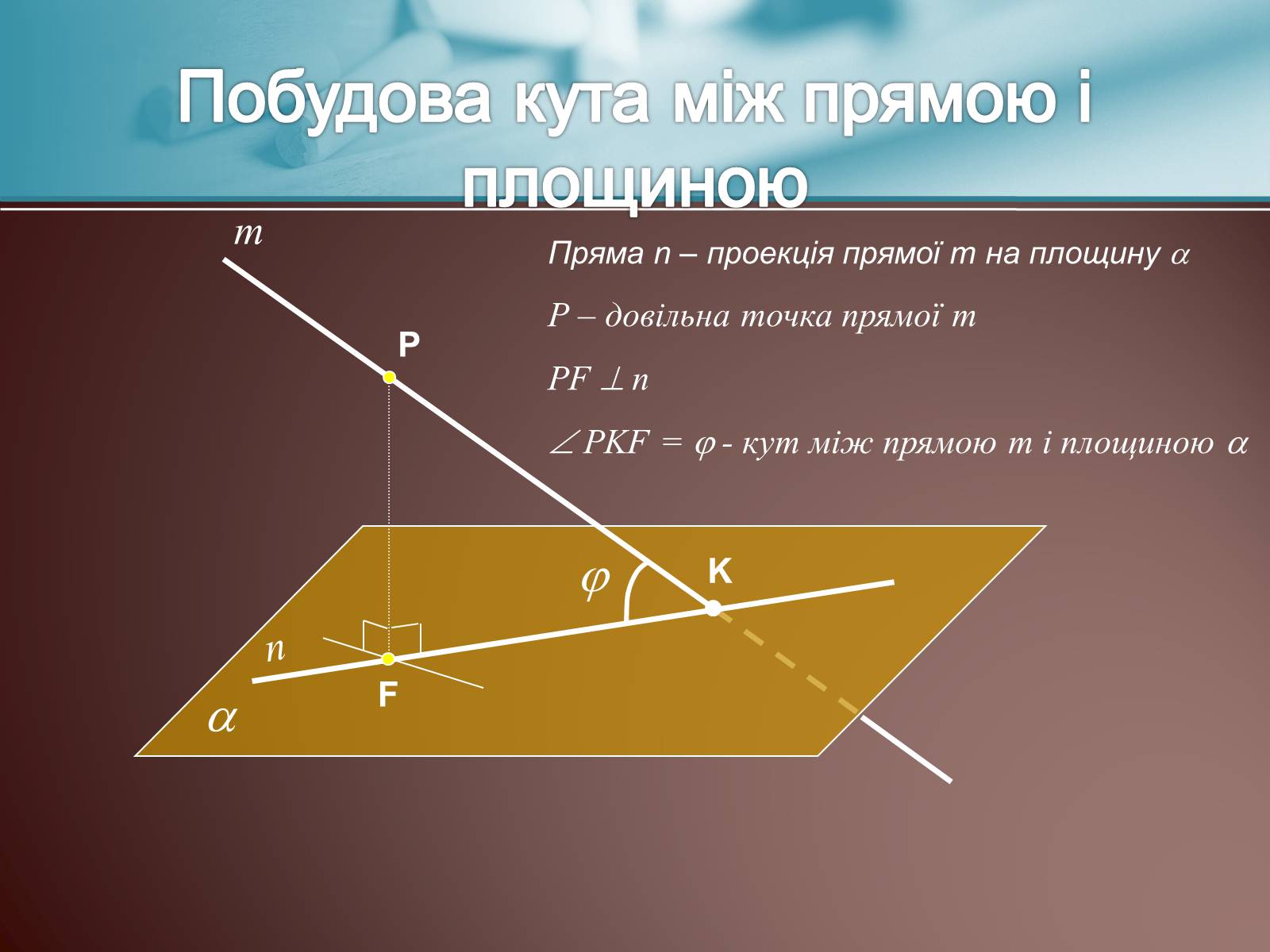
Побудова кута між прямою і площиною
т
n
K
Пряма n – проекція прямої m на площину
Р – довільна точка прямої m
PF n
PKF = - кут між прямою m і площиною
P
F
т
n
K
Пряма n – проекція прямої m на площину
Р – довільна точка прямої m
PF n
PKF = - кут між прямою m і площиною
P
F
Слайд #19
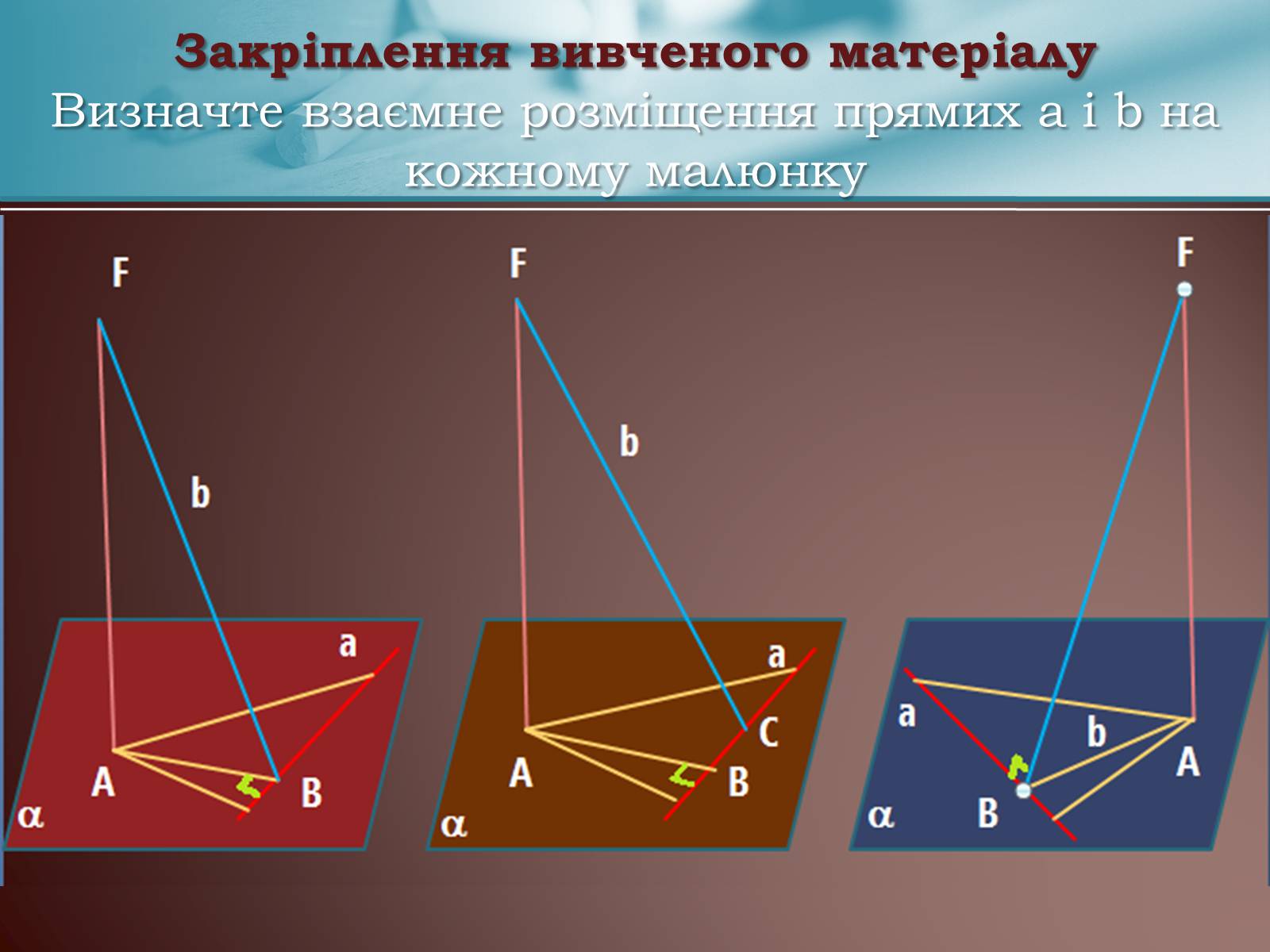
Закріплення вивченого матеріалуВизначте взаємне розміщення прямих а і b на кожному малюнку
Слайд #20
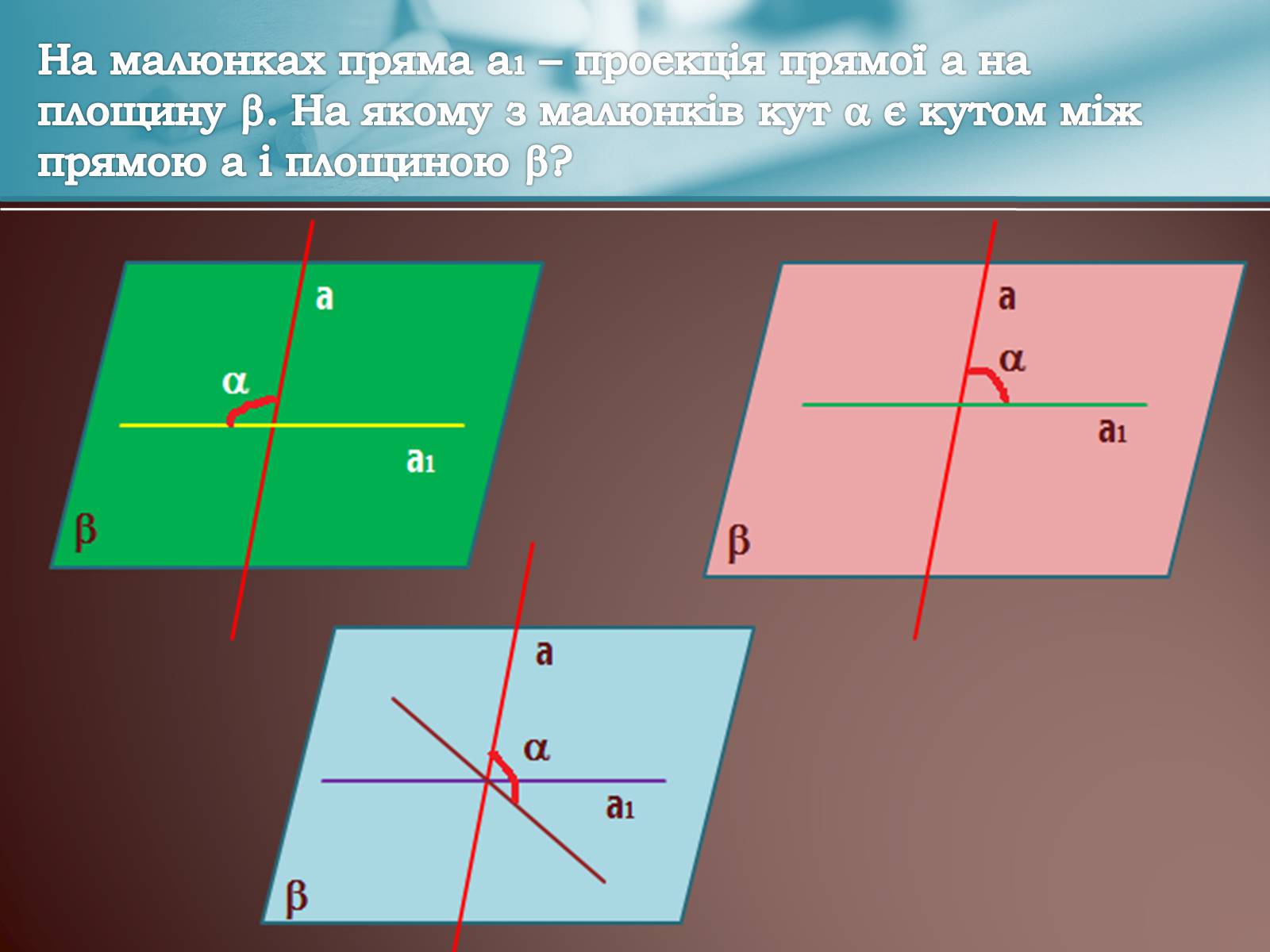
На малюнках пряма а1 – проекція прямої а на площину . На якому з малюнків кут є кутом між прямою а і площиною ?
Слайд #21
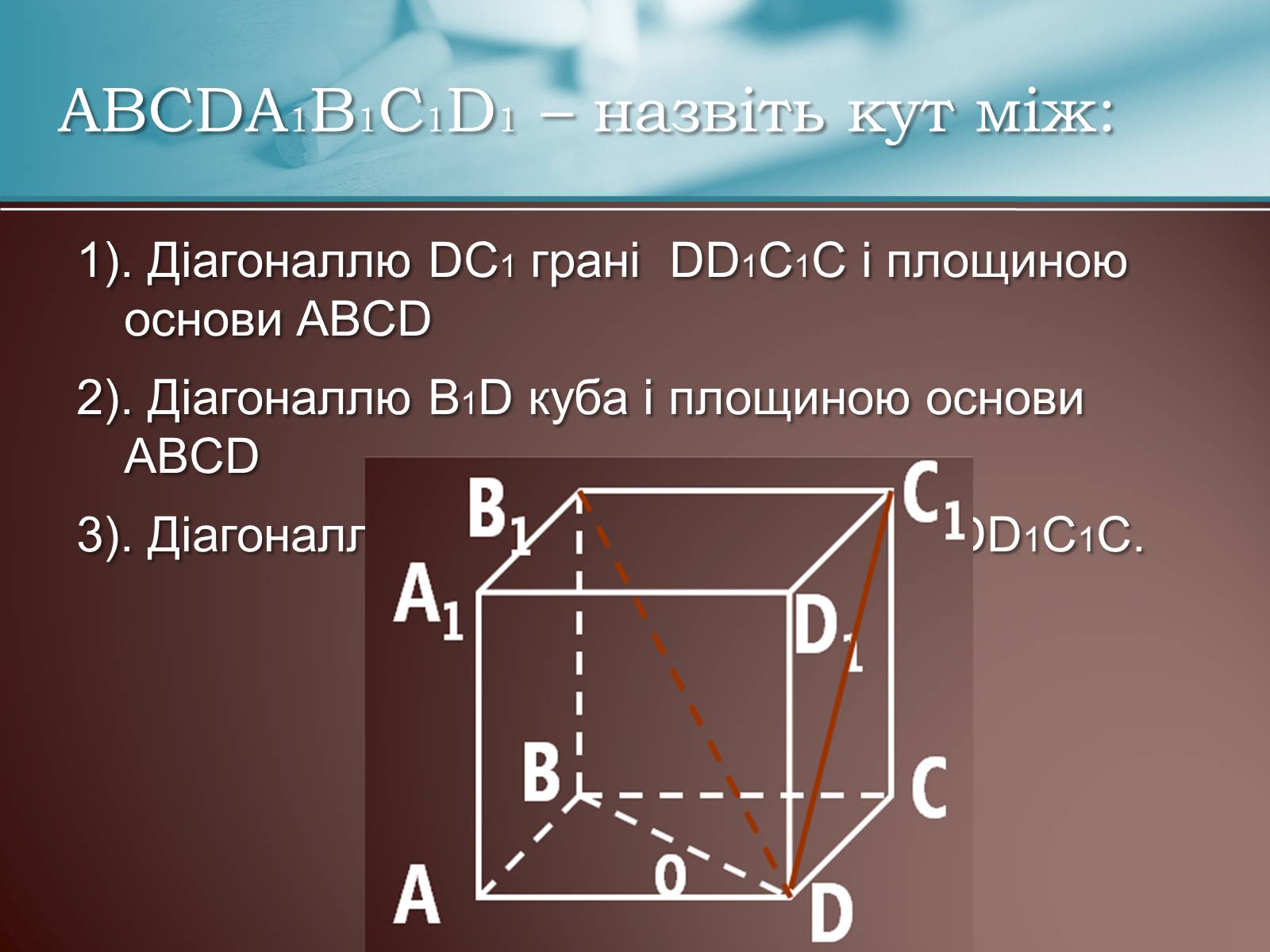
1). Діагоналлю DC1 грані DD1C1C і площиною основи ABCD
2). Діагоналлю B1D куба і площиною основи ABCD
3). Діагоналлю B1D і площиною грані DD1C1C.
ABCDA1B1C1D1 – назвіть кут між:
2). Діагоналлю B1D куба і площиною основи ABCD
3). Діагоналлю B1D і площиною грані DD1C1C.
ABCDA1B1C1D1 – назвіть кут між:
Слайд #22
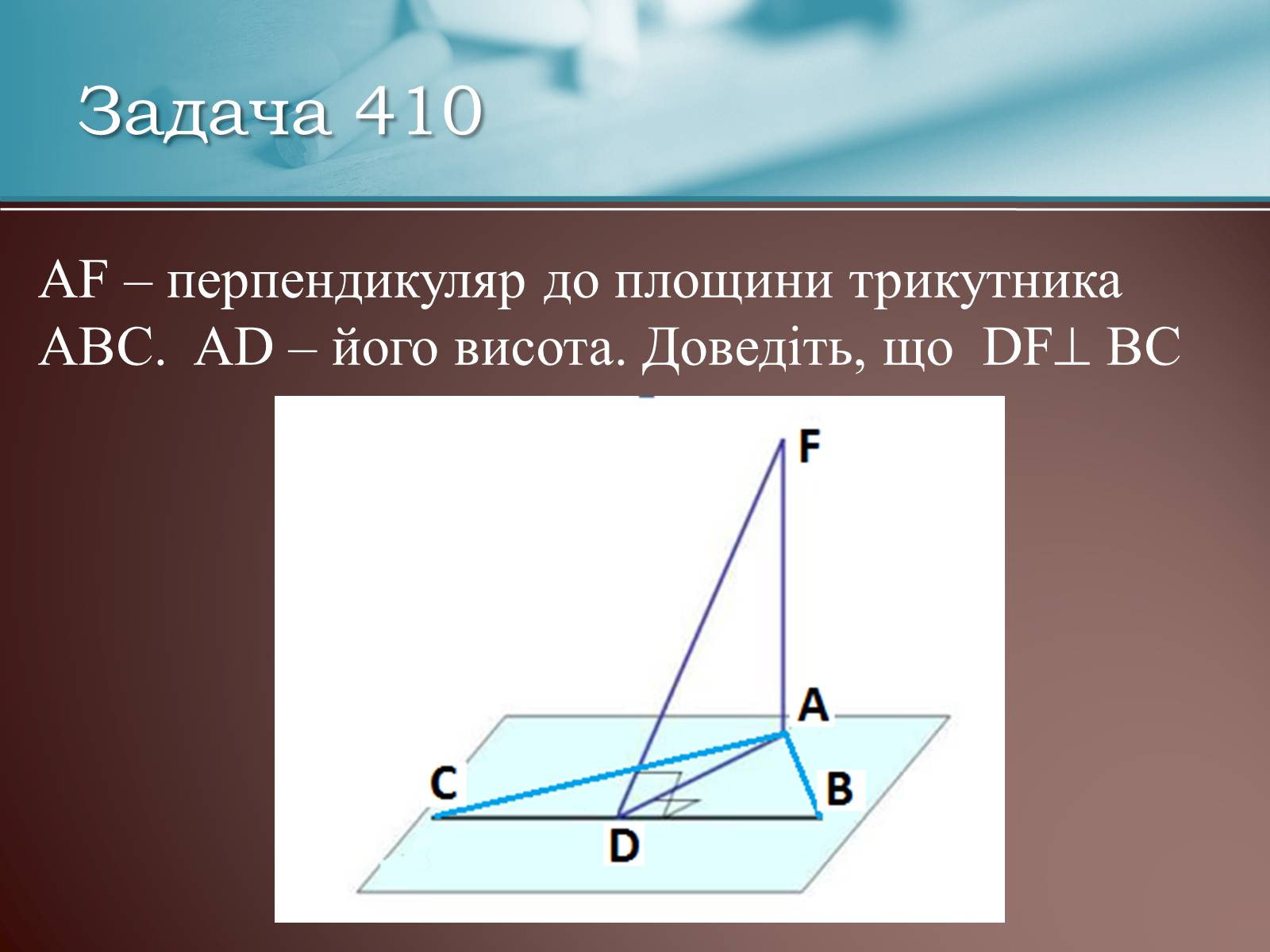
Задача 410
AF – перпендикуляр до площини трикутника АВС. AD – його висота. Доведіть, що DF ВC
AF – перпендикуляр до площини трикутника АВС. AD – його висота. Доведіть, що DF ВC
Слайд #23
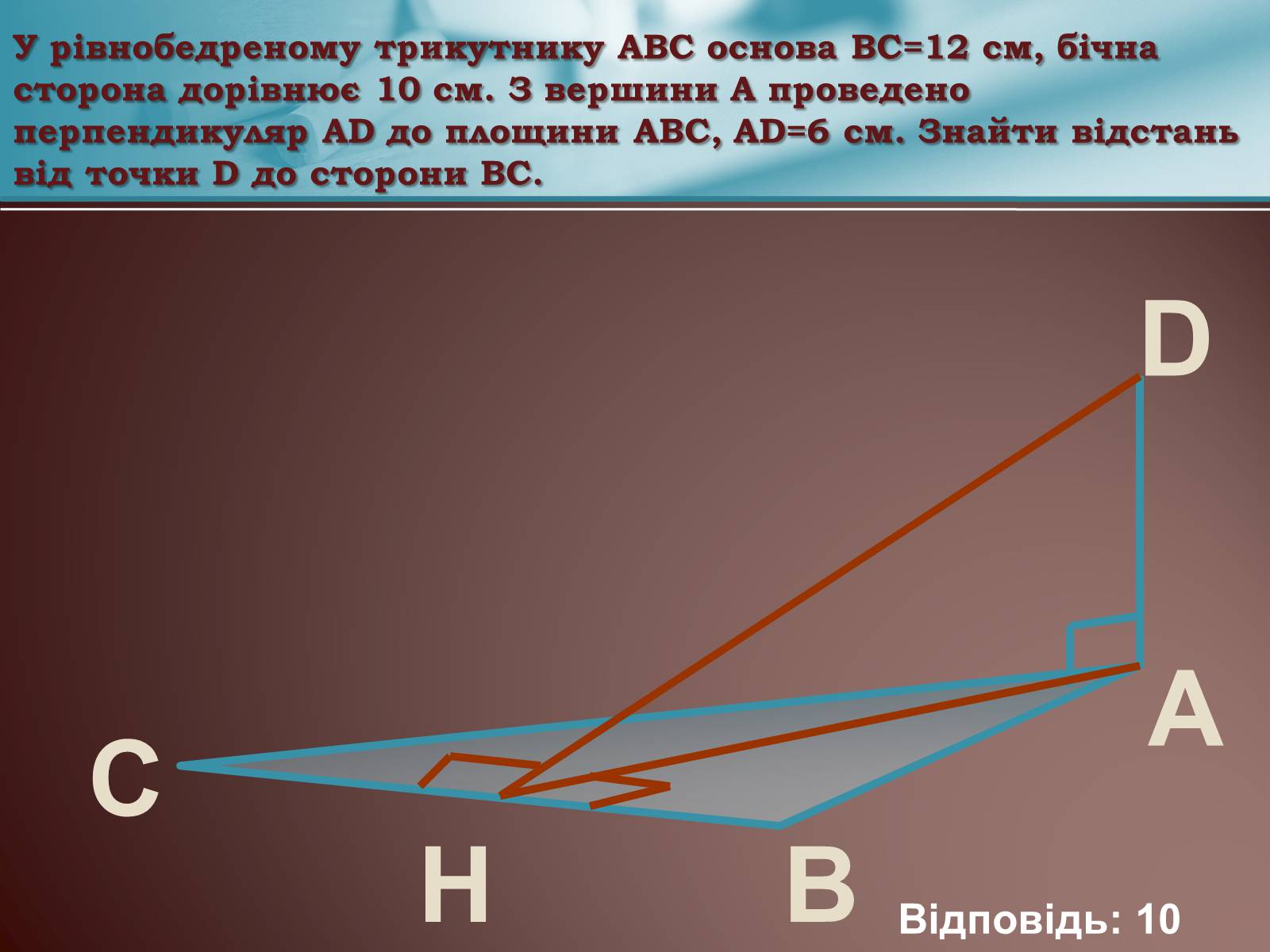
У рівнобедреному трикутнику АВС основа ВС=12 см, бічна сторона дорівнює 10 см. З вершини А проведено перпендикуляр АD до площини АВС, АD=6 см. Знайти відстань від точки D до сторони ВС.
B
А
С
D
Н
Відповідь: 10 см
B
А
С
D
Н
Відповідь: 10 см
Слайд #24
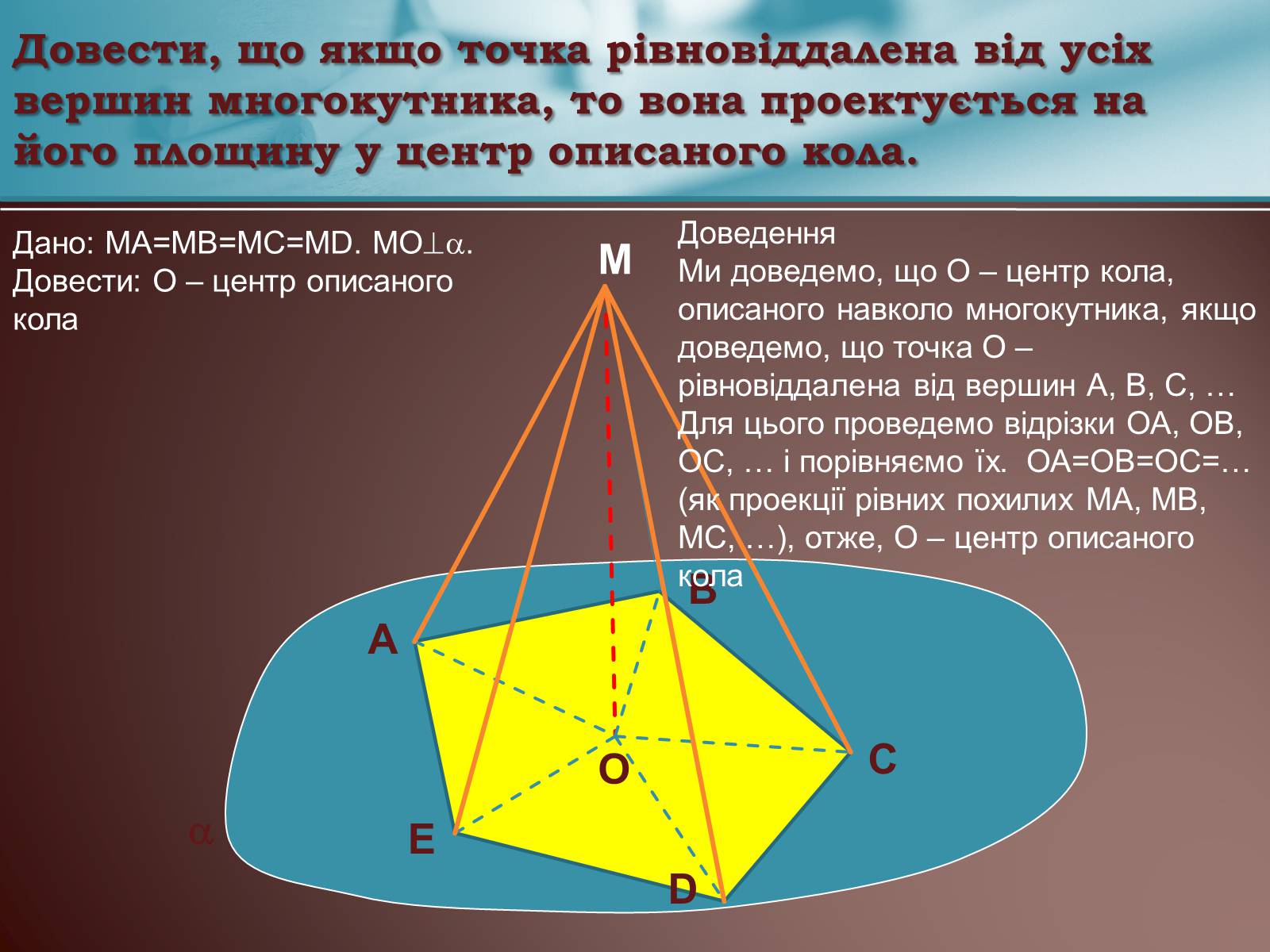
Довести, що якщо точка рівновіддалена від усіх вершин многокутника, то вона проектується на його площину у центр описаного кола.
M
A
B
C
D
E
O
Дано: МА=МВ=МС=МD. МО.
Довести: О – центр описаного кола
Доведення
Ми доведемо, що О – центр кола, описаного навколо многокутника, якщо доведемо, що точка О – рівновіддалена від вершин А, В, С, …
Для цього проведемо відрізки ОА, ОВ, ОС, … і порівняємо їх. ОА=ОВ=ОС=… (як проекції рівних похилих МА, МВ, МС, …), отже, О – центр описаного кола
M
A
B
C
D
E
O
Дано: МА=МВ=МС=МD. МО.
Довести: О – центр описаного кола
Доведення
Ми доведемо, що О – центр кола, описаного навколо многокутника, якщо доведемо, що точка О – рівновіддалена від вершин А, В, С, …
Для цього проведемо відрізки ОА, ОВ, ОС, … і порівняємо їх. ОА=ОВ=ОС=… (як проекції рівних похилих МА, МВ, МС, …), отже, О – центр описаного кола
Слайд #25
Якщо точка рівновіддалена від усіх вершин многокутника, то основою перпендикуляра, опущеного з даної точки на площину многокутника, є центр кола, описаного навколо даного многокутника.
Висновок 2
Висновок 2
