Презентація на тему «Правильні многогранники» (варіант 1)
257
Слайд #1
ПРАВИЛЬНІ МНОГОГРАННИКИ
Правильних многогранників надзвичайно мало, але це дуже скромний за кількістю загін зумів пробитися у найбільші глибини різних наук
Льюїс Керролл
Правильних многогранників надзвичайно мало, але це дуже скромний за кількістю загін зумів пробитися у найбільші глибини різних наук
Льюїс Керролл
Слайд #2
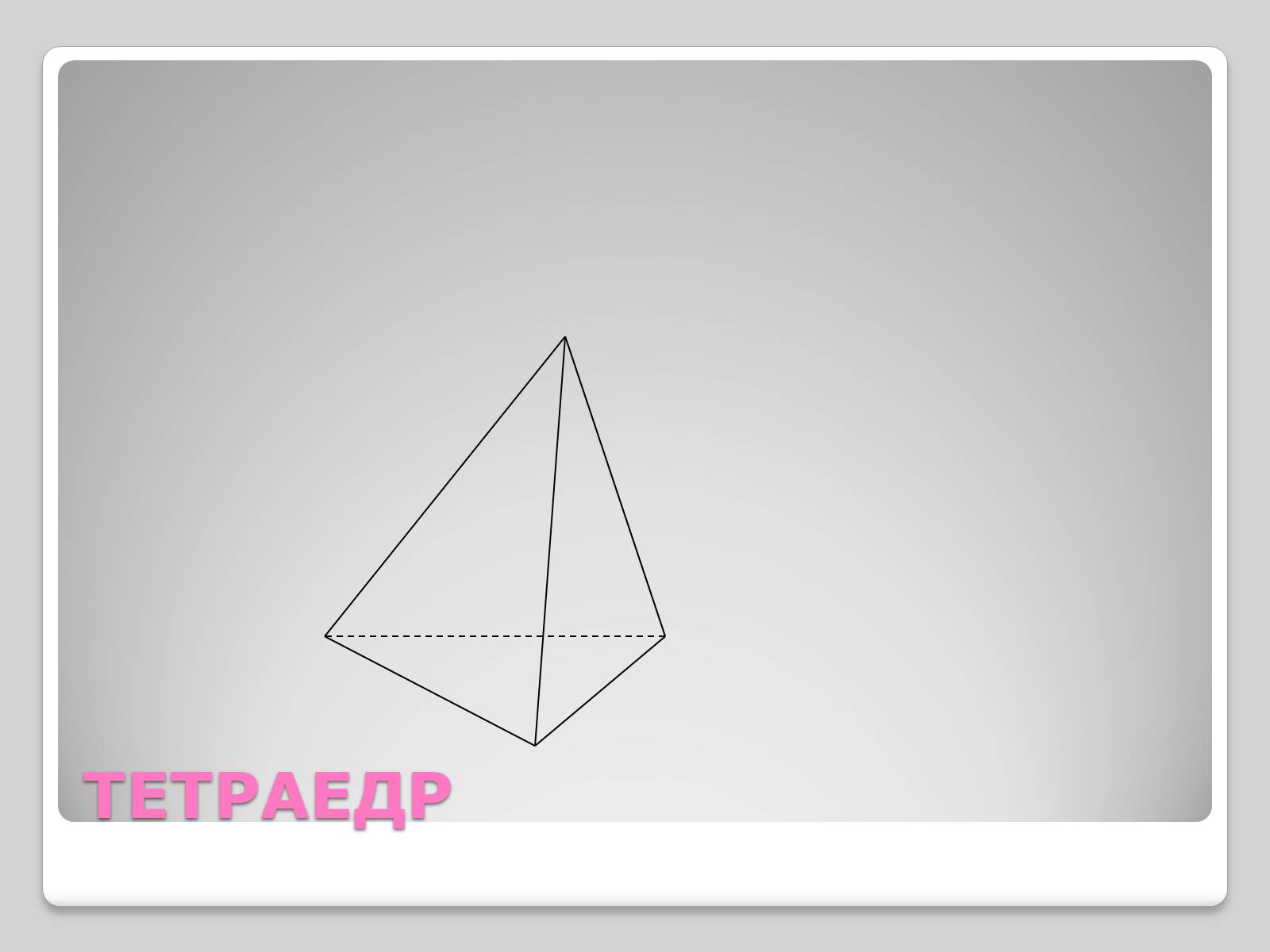
ТЕТРАЕДР
Слайд #3
І група “ Тетраедр”
Правильним тетраедром називається многранник у якого всі грані – правильні трикутники і в кожній вершині сходиться 3 ребра.
Елементи: tttКількісні характеристики:
Вершин – 4
Ребер – 6
Граней – 4
Правильним тетраедром називається многранник у якого всі грані – правильні трикутники і в кожній вершині сходиться 3 ребра.
Елементи: tttКількісні характеристики:
Вершин – 4
Ребер – 6
Граней – 4
Слайд #4
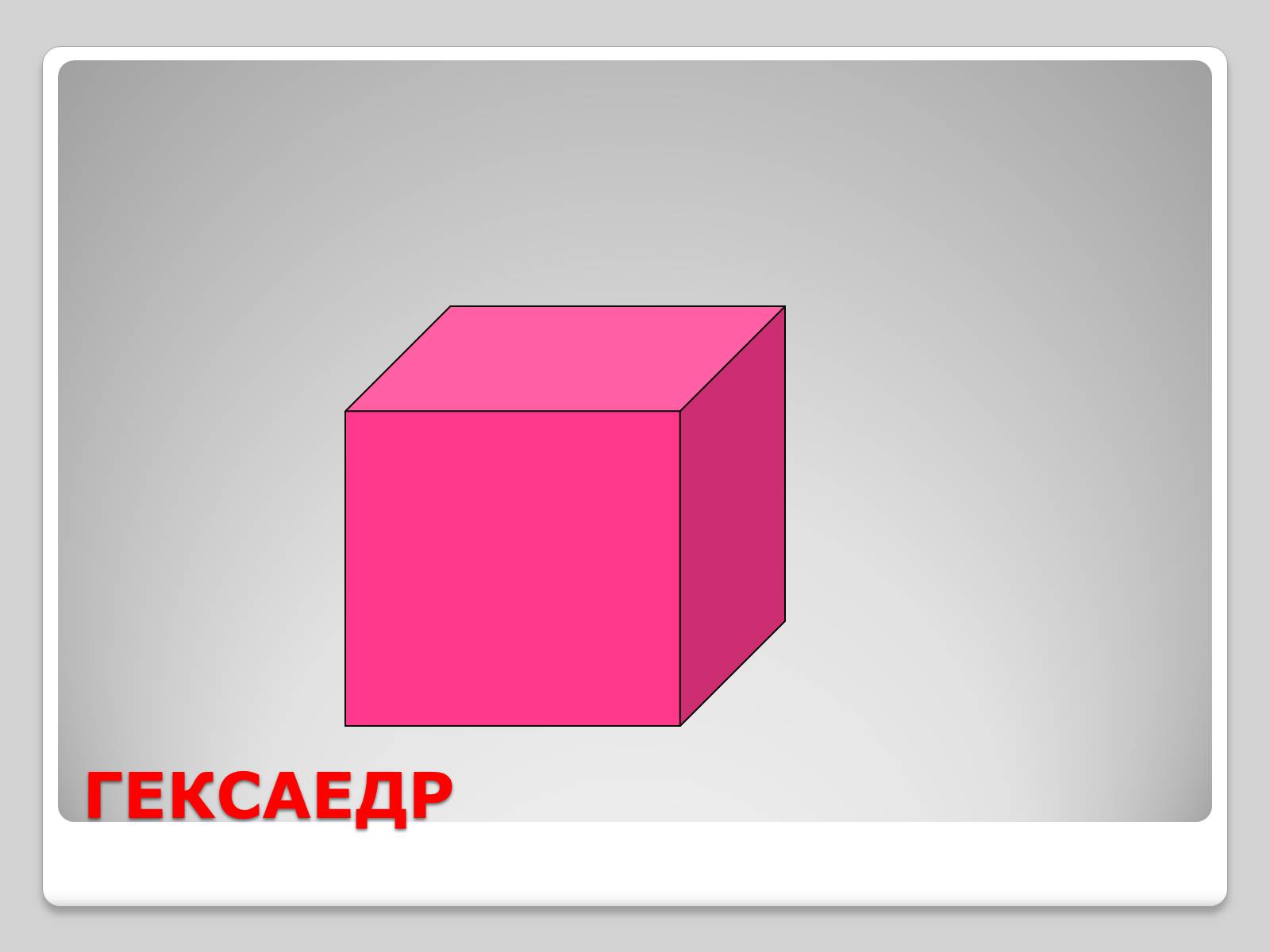
ГЕКСАЕДР
Слайд #5
ІІ група “Гексаедр”
У куба всі грані – квадрати, у кожній вершині сходиться по три ребра.
Куб – це прямокутний паралелепіпед, у якого всі ребра рівні.
Елементи: Кількісні характеристики :
Граней – 6
Ребер – 12
Вершин - 8
У куба всі грані – квадрати, у кожній вершині сходиться по три ребра.
Куб – це прямокутний паралелепіпед, у якого всі ребра рівні.
Елементи: Кількісні характеристики :
Граней – 6
Ребер – 12
Вершин - 8
Слайд #6
Факти
Античні вчені вважали, що атоми Землі мають форму гексаедра.
Форму куба мають кристали кухонної солі, деякі алмази та кристали.
Античні вчені вважали, що атоми Землі мають форму гексаедра.
Форму куба мають кристали кухонної солі, деякі алмази та кристали.
Слайд #7
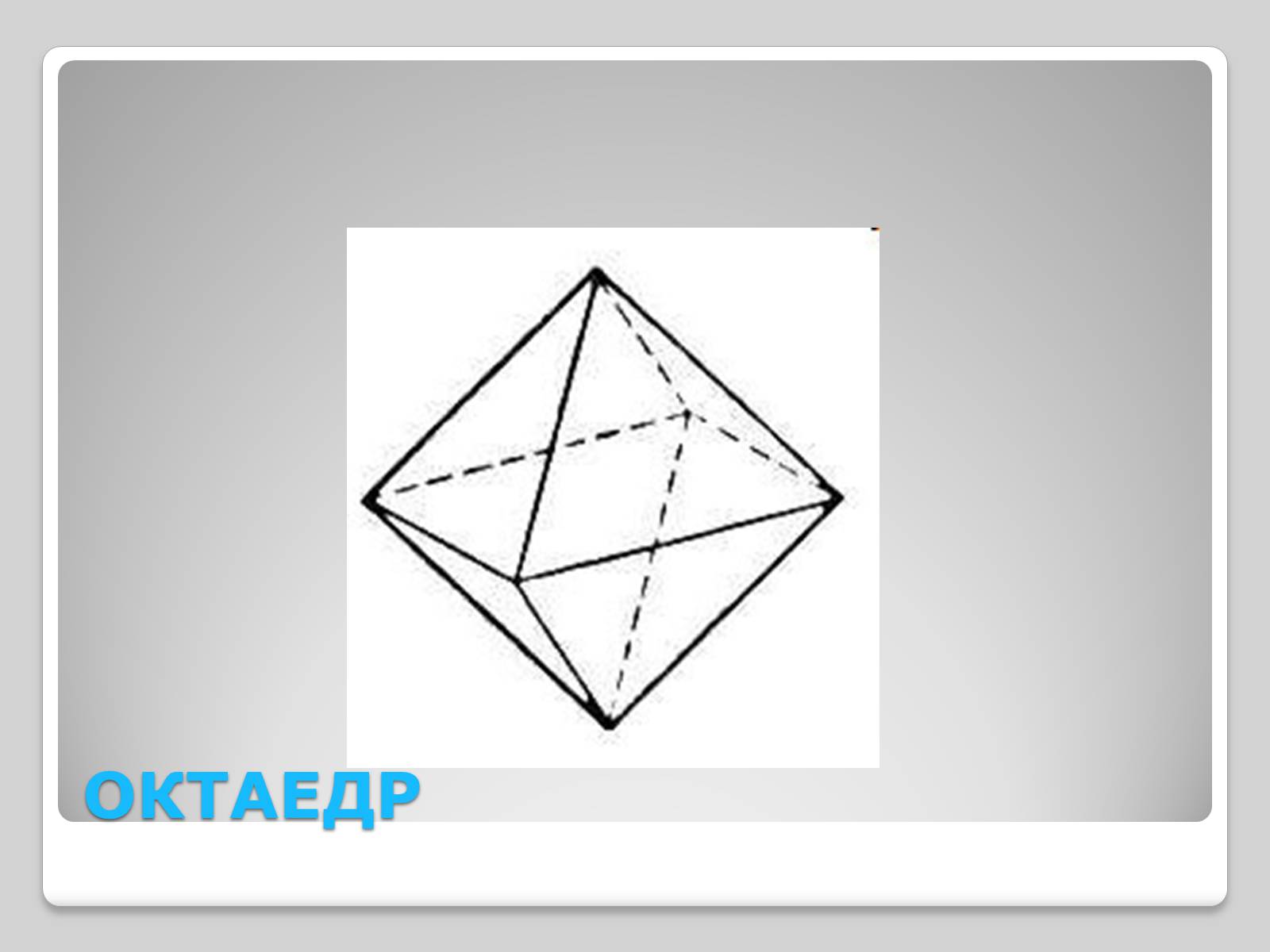
ОКТАЕДР
Слайд #8
ІІІ група “Октаедр”
Октаедр – це правильний многогранник, у якого грані – правильні трикутники і в кожній вершині сходяться чотири ребра.
Елементи: tКількісні характеристики:
Граней – 8
Вершин – 6
Ребер - 12
Октаедр – це правильний многогранник, у якого грані – правильні трикутники і в кожній вершині сходяться чотири ребра.
Елементи: tКількісні характеристики:
Граней – 8
Вершин – 6
Ребер - 12
Слайд #9
Факти
Філософом Аполлонієм доведена теорема про відношення об'ємів октаедра та ікосаедра.
Це відношення таке саме, як і відношення площ їх поверхонь
Філософом Аполлонієм доведена теорема про відношення об'ємів октаедра та ікосаедра.
Це відношення таке саме, як і відношення площ їх поверхонь
Слайд #10
ІКОСАЕДР
Слайд #11
ІV група “Ікосаедр”
Ікосаедр – правильний многогранник, грані якого – правильні трикутники і в кожній вершині сходиться по 5 ребер.
Елементи t Кількісні характеристики
Вершин – 12
Ребер – 30
Граней - 20
Ікосаедр – правильний многогранник, грані якого – правильні трикутники і в кожній вершині сходиться по 5 ребер.
Елементи t Кількісні характеристики
Вершин – 12
Ребер – 30
Граней - 20
Слайд #12
Факти
Античні вчені вважали, що атоми води мають форму ікосаедра.
Античні вчені вважали, що атоми води мають форму ікосаедра.
Слайд #13
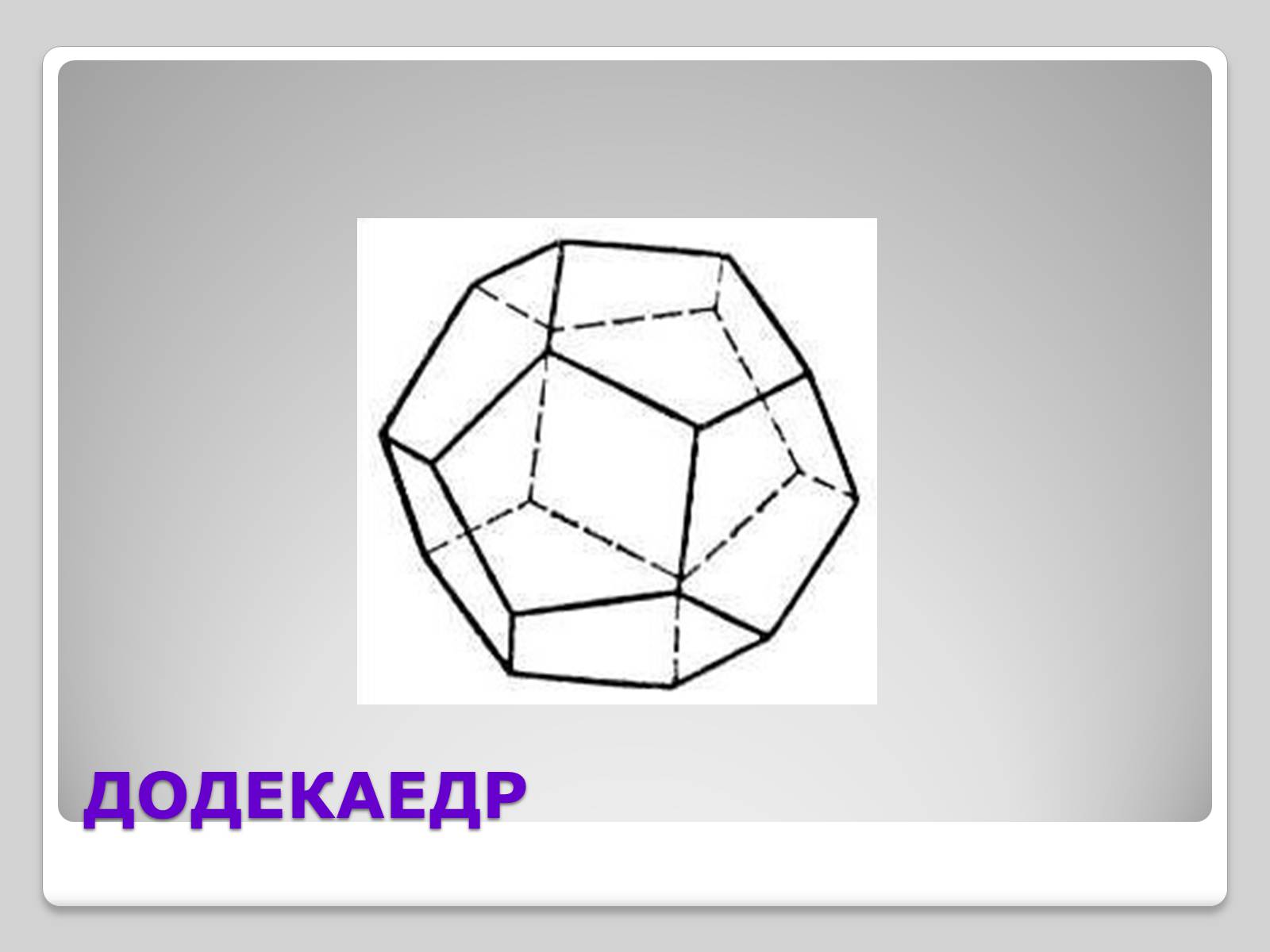
ДОДЕКАЕДР
Слайд #14
V група “Додекаедр”
Додекаедр – це такий правильний многогранник, грані якого – правильні п'ятикутники і в кожній вершині сходиться по 3 ребра.
Елементи Кількісні характеристики
Вершин – 20
Ребер – 30
Граней - 12
Додекаедр – це такий правильний многогранник, грані якого – правильні п'ятикутники і в кожній вершині сходиться по 3 ребра.
Елементи Кількісні характеристики
Вершин – 20
Ребер – 30
Граней - 12
Слайд #15
Факти
Античні вчені вважали, що форму додекаедра має Всесвіт.
Форму додекаедра мають кристали піриту (залізного колчедану)
Античні вчені вважали, що форму додекаедра має Всесвіт.
Форму додекаедра мають кристали піриту (залізного колчедану)
Слайд #16
Підсумок
Правильні многранники існували на Землі задовго до появи на ній людини – куби кам'яної солі, тетраедри сурянистого сірчанокислого натрію, октаедри хромових квасців, ікосаедри бору і додекаедри радіолярію та макроскопічних морських організмів.
Але тільки геометр побачив в них порядок і систему задовго до того, як фізики проникли в таємницю будови речовини.
Геометрія з її прозорою логікою, чіткістю побудов відкрила
зовсім нове бачення правильних многогранників та їх
нове застосування.
Правильні многранники існували на Землі задовго до появи на ній людини – куби кам'яної солі, тетраедри сурянистого сірчанокислого натрію, октаедри хромових квасців, ікосаедри бору і додекаедри радіолярію та макроскопічних морських організмів.
Але тільки геометр побачив в них порядок і систему задовго до того, як фізики проникли в таємницю будови речовини.
Геометрія з її прозорою логікою, чіткістю побудов відкрила
зовсім нове бачення правильних многогранників та їх
нове застосування.
