Презентація на тему «Теорія ймовірностей»
656
Слайд #1
Теорія ймовірностей
Підготувала учиниця 11-і класу
Білокінь Анастасія
Підготувала учиниця 11-і класу
Білокінь Анастасія
Слайд #2
Теорія ймовірностей — розділ математики, що вивчає закономірності випадкових явищ: випадкові події, випадкові величини, їхні функції, властивості й операції над ними.
Слайд #3
Математичним апаратом теорії ймовірностей є комбінаторика та теорія міри.
Теорія ймовірностей виникла і спершу розвивалася як прикладна дисципліна (зокрема, для розрахунків в азартних іграх).
Теорія ймовірностей виникла і спершу розвивалася як прикладна дисципліна (зокрема, для розрахунків в азартних іграх).
Слайд #4
зміст
Історія
Основні положення
Теми теорії ймовірностей
Кобінаторика
Історія
Основні положення
Теми теорії ймовірностей
Кобінаторика
Слайд #5
Виникнення теорії ймовірностей як науки відносять до середніх століть і першим спробам математичного аналізу азартних ігор. Спочатку її основні поняття не мали строго математичного вигляду, до них можна було ставитися як до деяких емпіричних фактів, властивостей реальних подій.
Історіявиникнення
Історіявиникнення
Слайд #6
Найранніші праці в галузі теорії ймовірностей належать до XVII століття. Досліджуючи прогнозування виграшу в азартних іграх, Блез Паскаль і П'єр Ферма відкрили перші ймовірнісні залежності, що виникають під час кидання гральних кубиків.
Слайд #7
Справжню наукову основу теорії ймовірностей заклав великий математик Якоб Бернуллі . Його праця «Мистецтва припущень» стала першим ґрунтовним трактатом з теорії ймовірностей.
А сформульований Бернуллі закон великих чисел дав можливість встановити зв'язок між імовірністю будь-якої випадкової події та частотою її появи, яка спостерігається безпосередньо з досвіду.
А сформульований Бернуллі закон великих чисел дав можливість встановити зв'язок між імовірністю будь-якої випадкової події та частотою її появи, яка спостерігається безпосередньо з досвіду.
Слайд #8
Основні положення
Під випробуванням мається на увазі здійснення запланованих дій і отримання результату за виконання певного комплексу умов S. При цьому припускається, що ці умови є фіксованими; вони або об'єктивно існують, або створюються штучно й можуть бути відтворені необмежену кількість разів.
Під випробуванням мається на увазі здійснення запланованих дій і отримання результату за виконання певного комплексу умов S. При цьому припускається, що ці умови є фіксованими; вони або об'єктивно існують, або створюються штучно й можуть бути відтворені необмежену кількість разів.
Слайд #9
Прикладами випробування: виготовлення деталі або виробу, кидання монети або грального кубика, розігрування лотереї, проведення аукціону.
Слайд #10
Результатом випробування є подія. Події поділяються на: правдиві (однозначно відбудуться), неможливі, випадкові, сумісні, несумісні. Позначаються великими латинськими літерами, наприклад, А, B, С.
Слайд #11
Основні об'єкти дослідження теорії ймовірностей:
Слайд #12
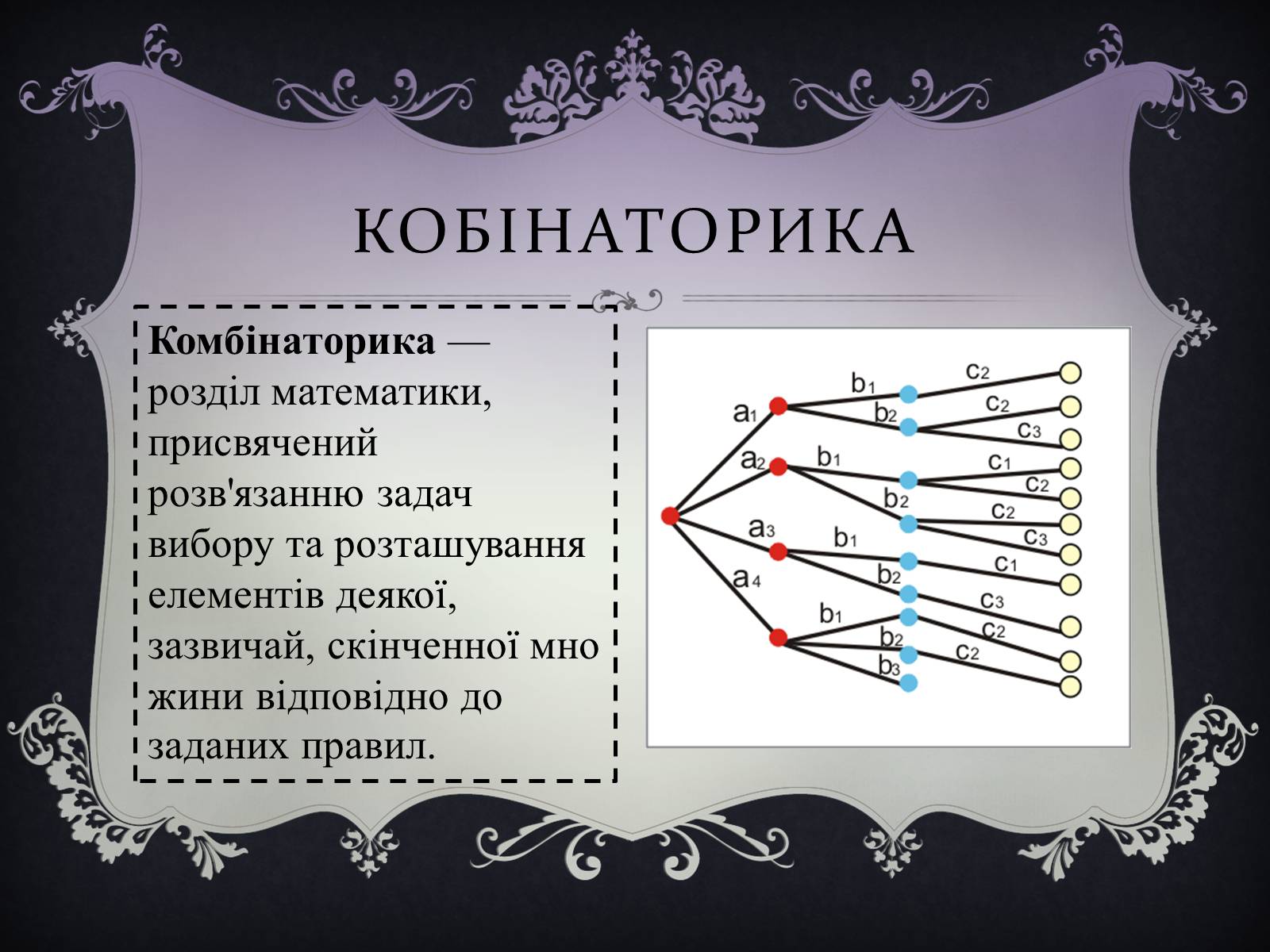
Кобінаторика
Комбінаторика — розділ математики, присвячений розв'язанню задач вибору та розташування елементів деякої, зазвичай, скінченної множини відповідно до заданих правил.
Комбінаторика — розділ математики, присвячений розв'язанню задач вибору та розташування елементів деякої, зазвичай, скінченної множини відповідно до заданих правил.
Слайд #13
На меті комбінаторного аналізу стоїть дослідження комбінаторних конфігурацій, алгоритмів їх побудови, оптимізація таких алгоритмів, а також розв'язання задач переліку.
Найпростішими прикладами комбінаторних конфігурацій є перестановки, розміщення, комбінація та розбиття.
Назад
Найпростішими прикладами комбінаторних конфігурацій є перестановки, розміщення, комбінація та розбиття.
Назад
Слайд #14
Відео
