- Головна
- Готові шкільні презентації
- Презентація на тему «Симметрия в нашей жизни»
Презентація на тему «Симметрия в нашей жизни»
279
Слайд #1
Симметрия в нашей жизни
Подготовили ученицы 11Б класса :
Осадчук Валерия Григор Татьяна
Подготовили ученицы 11Б класса :
Осадчук Валерия Григор Татьяна

Слайд #2
Содержание
Определение симметрии
Центральная симметрия
Осевая симметрия
Симметрия вращения
Зеркальная симметрия
Симметрия подобия
Симметрия растений
Симметрия животных
Симметрия в архитектуре
Человек- существо симметричное?
Симметрия слов и чисел
Определение симметрии
Центральная симметрия
Осевая симметрия
Симметрия вращения
Зеркальная симметрия
Симметрия подобия
Симметрия растений
Симметрия животных
Симметрия в архитектуре
Человек- существо симметричное?
Симметрия слов и чисел
Слайд #3
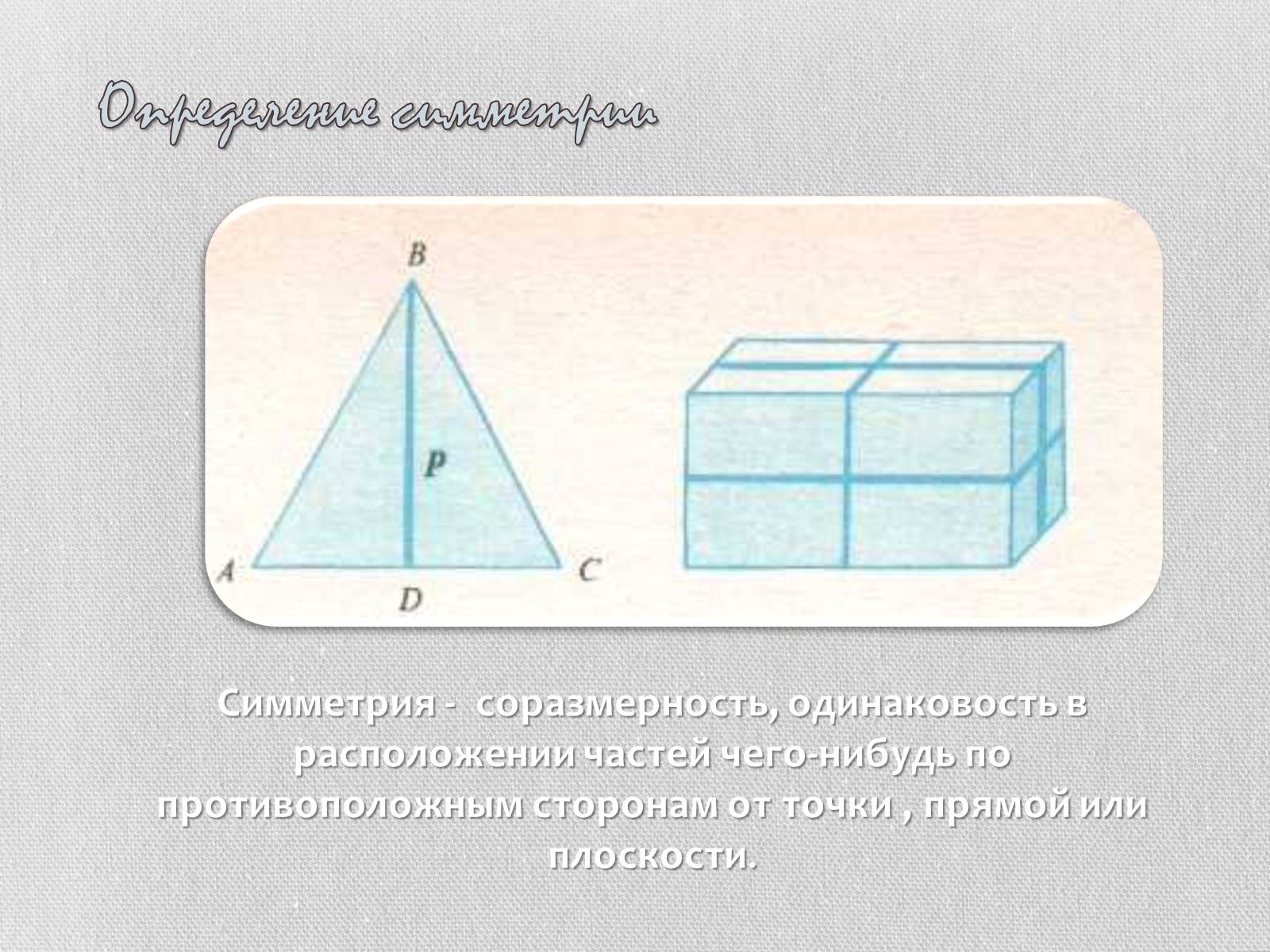
Определение симметрии
Симметрия - соразмерность, одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки , прямой или плоскости.
Симметрия - соразмерность, одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки , прямой или плоскости.
Слайд #4
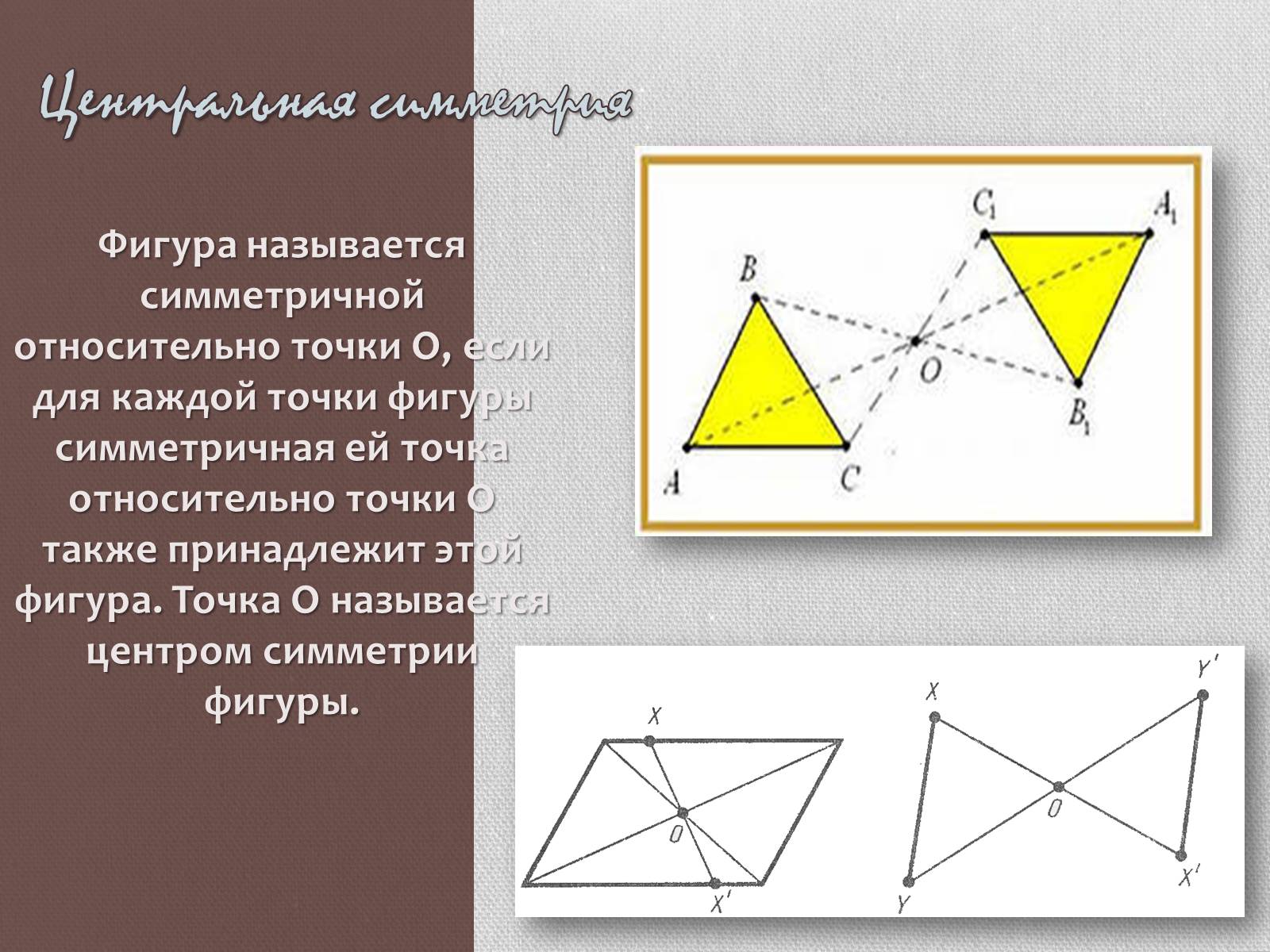
Центральная симметрия
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигура. Точка О называется центром симметрии фигуры.
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигура. Точка О называется центром симметрии фигуры.
Слайд #5
Примерами фигур, обладающих центральной симметрией , являются окружность и параллелограмм. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма- точка пересечения диагоналей. Любая прямая также обладает центральной симметрией . График нечетной функции симметричен относительно начала координат.
Примером фигуры, не имеющей центра симметрии , является произвольный треугольник.
Примером фигуры, не имеющей центра симметрии , является произвольный треугольник.

Слайд #6
Симметрия относительно плоскости
Симметрия относительно плоскости - это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону плоскости, всегда будет соответствовать точка, расположенная по другую сторону плоскости, а отрезки, соединяющие эти точки, будут перпендикулярны плоскости симметрии и делятся ею пополам.
Две симметричные фигуры или две симметричные части одной фигуры при всем их сходстве, равенстве объемов и площадей поверхностей, в общем случае, неравны, т.е. их нельзя совместить друг с другом Это разные фигуры, их нельзя заменить друг другом, например, правая перчатка, ботинок и т.д. не годятся для левой руки, ноги.
Предметы могут иметь одну, две, три и т.д. плоскостей симметрии.
Симметрия относительно плоскости - это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону плоскости, всегда будет соответствовать точка, расположенная по другую сторону плоскости, а отрезки, соединяющие эти точки, будут перпендикулярны плоскости симметрии и делятся ею пополам.
Две симметричные фигуры или две симметричные части одной фигуры при всем их сходстве, равенстве объемов и площадей поверхностей, в общем случае, неравны, т.е. их нельзя совместить друг с другом Это разные фигуры, их нельзя заменить друг другом, например, правая перчатка, ботинок и т.д. не годятся для левой руки, ноги.
Предметы могут иметь одну, две, три и т.д. плоскостей симметрии.

Слайд #7
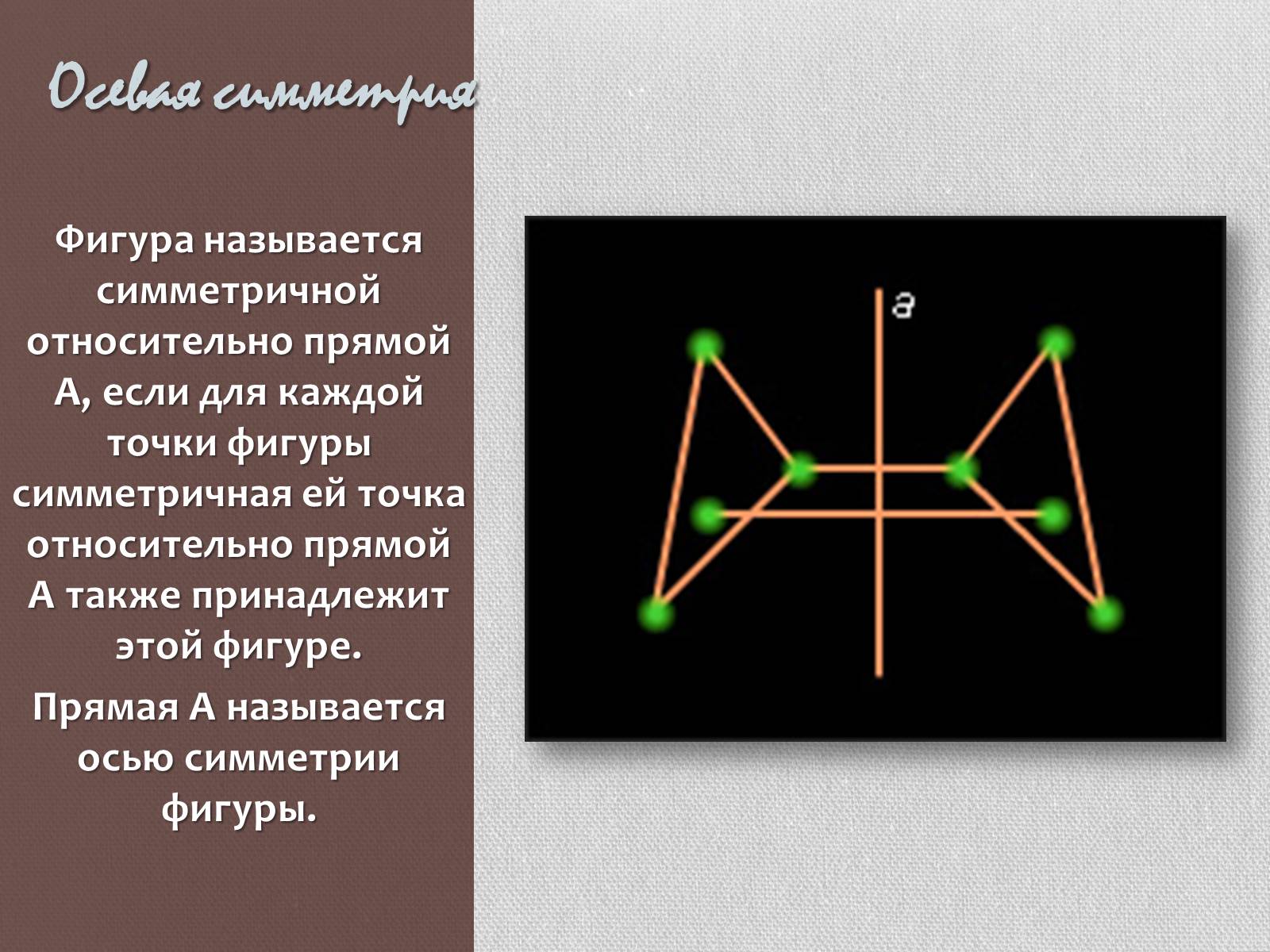
Осевая симметрия
Фигура называется симметричной относительно прямой А, если для каждой точки фигуры симметричная ей точка относительно прямой А также принадлежит этой фигуре.
Прямая А называется осью симметрии фигуры.
Фигура называется симметричной относительно прямой А, если для каждой точки фигуры симметричная ей точка относительно прямой А также принадлежит этой фигуре.
Прямая А называется осью симметрии фигуры.
Слайд #8
Симметрия вращения
Симметрия вращения - это такое свойство геометрической фигуры, когда при повороте этой фигуры на угол a =360°/n около некоторой оси вращения она совместится со своим первоначальным положением.
Симметрия вращения - это такое свойство геометрической фигуры, когда при повороте этой фигуры на угол a =360°/n около некоторой оси вращения она совместится со своим первоначальным положением.

Слайд #9
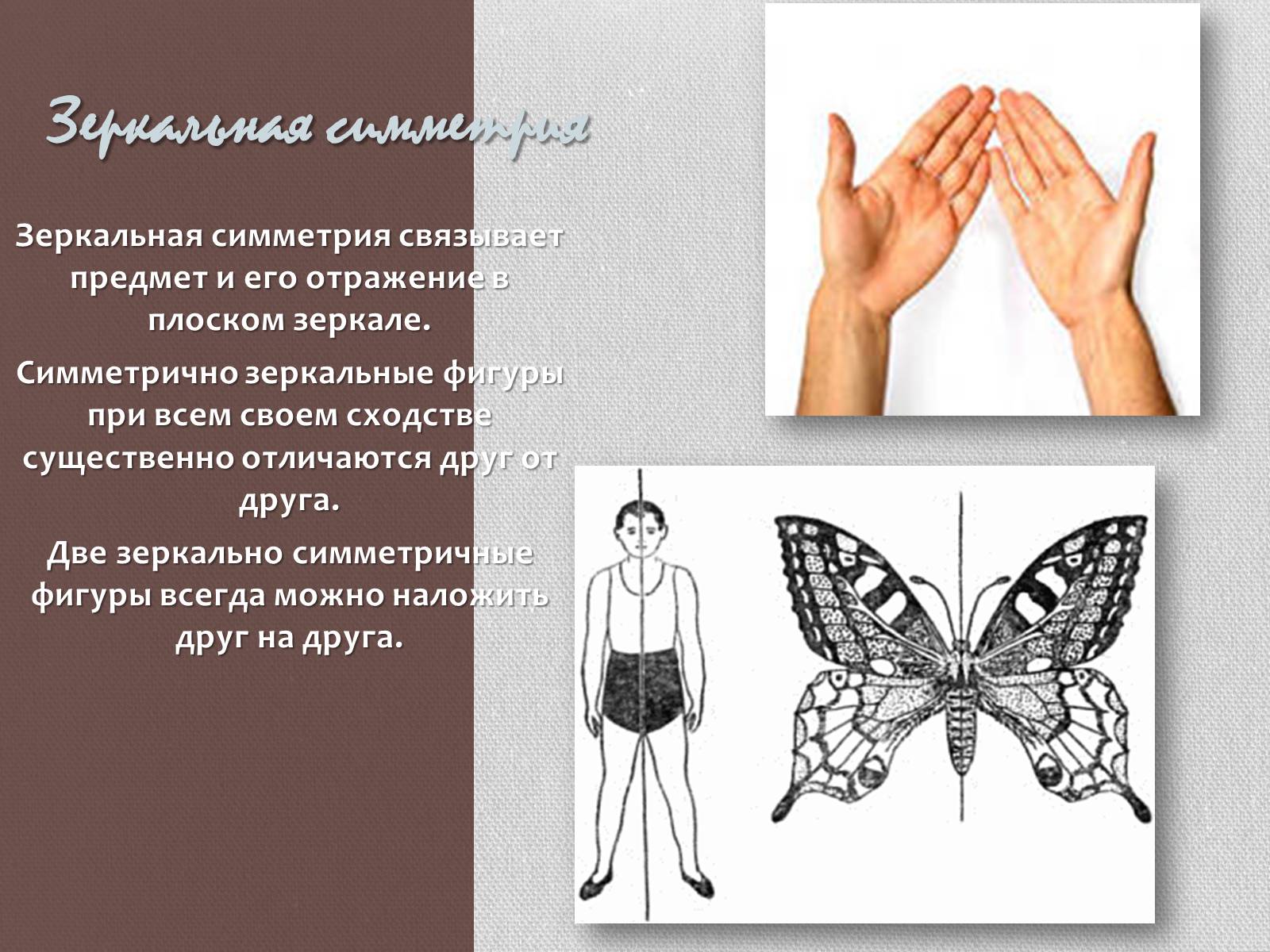
Зеркальная симметрия
Зеркальная симметрия связывает предмет и его отражение в плоском зеркале.
Симметрично зеркальные фигуры при всем своем сходстве существенно отличаются друг от друга.
Две зеркально симметричные фигуры всегда можно наложить друг на друга.
Зеркальная симметрия связывает предмет и его отражение в плоском зеркале.
Симметрично зеркальные фигуры при всем своем сходстве существенно отличаются друг от друга.
Две зеркально симметричные фигуры всегда можно наложить друг на друга.
Слайд #10
Симметрия подобия
Симметрия подобия представляет собой аналоги предыдущих симметрий с той лишь разницей ,что они связаны с одновременным уменьшением или увеличением частей фигуры и расстояний между ними. Простейшим примером такой симметрии являются матрешки. Симметрией подобия могут обладать буквы: Ж, Н , М , О , А .
Симметрия подобия представляет собой аналоги предыдущих симметрий с той лишь разницей ,что они связаны с одновременным уменьшением или увеличением частей фигуры и расстояний между ними. Простейшим примером такой симметрии являются матрешки. Симметрией подобия могут обладать буквы: Ж, Н , М , О , А .

Слайд #11
Симметрия растений
Характерная для растений симметрия конуса хорошо видна на примере любого дерева.
У цветковых растений в большинстве проявляется радиальная и билатеральная симметрия. Цветок считается симметричным, когда каждый околоцветник состоит из равного числа частей.
Характерная для растений симметрия конуса хорошо видна на примере любого дерева.
У цветковых растений в большинстве проявляется радиальная и билатеральная симметрия. Цветок считается симметричным, когда каждый околоцветник состоит из равного числа частей.

Слайд #12
Симметрия животных
Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии.
Сферическая симметрия имеет место у радиолярий и солнечников, тела которых сферической формы
При радиальной или лучистой симметрии тело имеет форму короткого или длинного цилиндра либо сосуда с центральной осью, от которого отходят в радиальном порядке части тела. Это кишечнополостные, иглокожие, морские звёзды.
Билатеральная (зеркальная) симметрия – характерная симметрия всех представителей животного мира.
Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии.
Сферическая симметрия имеет место у радиолярий и солнечников, тела которых сферической формы
При радиальной или лучистой симметрии тело имеет форму короткого или длинного цилиндра либо сосуда с центральной осью, от которого отходят в радиальном порядке части тела. Это кишечнополостные, иглокожие, морские звёзды.
Билатеральная (зеркальная) симметрия – характерная симметрия всех представителей животного мира.

Слайд #13
Симметрия в архитектуре
Симметрия сооружения связывается с организацией его функций. Проекция плоскости симметрии — ось здания — определяет обычно размещение главного входа и начало основных потоков движения.
Каждая деталь в симметричной системе существует как двойник своей обязательной паре, расположенной по другую сторону оси, и благодаря этому она может рассматриваться лишь как часть целого.
Наиболее распространена в архитектуре зеркальная симметрия. Ей подчинены постройки Древнего Египта и храмы античной Греции, амфитеатры, термы, базилики и триумфальные арки римлян, дворцы и церкви Ренессанса, равно как и многочисленные сооружения современной архитектуры.
Симметрия сооружения связывается с организацией его функций. Проекция плоскости симметрии — ось здания — определяет обычно размещение главного входа и начало основных потоков движения.
Каждая деталь в симметричной системе существует как двойник своей обязательной паре, расположенной по другую сторону оси, и благодаря этому она может рассматриваться лишь как часть целого.
Наиболее распространена в архитектуре зеркальная симметрия. Ей подчинены постройки Древнего Египта и храмы античной Греции, амфитеатры, термы, базилики и триумфальные арки римлян, дворцы и церкви Ренессанса, равно как и многочисленные сооружения современной архитектуры.

Слайд #14
Человек- существо симметричное?
Никто не усомнится, что внешне человек построен симметрично: левой руке всегда соответствует правая и обе руки совершенно одинаковы. Но сходство между нашими руками, ушами, глазами и другими частями тела такое же, как между предметом и его отражением в зеркале.
Асимметрия лица статуи Венеры Милосской, созданной древнегреческим скульптором, выражается смещением носа вправо от средней линии, в более высоком положении левой ушной раковины и левой глазницы и меньшим расстоянием от срединной линии левой глазницы, чем правой.
Сторонники симметрии критиковали несимметричность форм этого общепризнанного эталона женской красоты, полагая, что лицо Венеры было бы гораздо красивее, если бы оно было симметричным.
Никто не усомнится, что внешне человек построен симметрично: левой руке всегда соответствует правая и обе руки совершенно одинаковы. Но сходство между нашими руками, ушами, глазами и другими частями тела такое же, как между предметом и его отражением в зеркале.
Асимметрия лица статуи Венеры Милосской, созданной древнегреческим скульптором, выражается смещением носа вправо от средней линии, в более высоком положении левой ушной раковины и левой глазницы и меньшим расстоянием от срединной линии левой глазницы, чем правой.
Сторонники симметрии критиковали несимметричность форм этого общепризнанного эталона женской красоты, полагая, что лицо Венеры было бы гораздо красивее, если бы оно было симметричным.

Слайд #15
Симметрия слов и чисел
Палиндром- это некоторый объект, в котором задана симметрия составляющих от начала к концу и от конца к началу. Например фраза или текст.
Прямой текст палиндрома, читающийся в соответствии с нормальным направлением чтения в данной письменности (во всех видах кириллической и латинской письменности – слева направо), называется прямоходом, обратный – ракоходом или реверсом (справа налево).
Некоторые числа тоже обладают симметрией.
Тропа на лево повела, на порт
Леша на полке клопа нашел
6996
2002
101
Палиндром- это некоторый объект, в котором задана симметрия составляющих от начала к концу и от конца к началу. Например фраза или текст.
Прямой текст палиндрома, читающийся в соответствии с нормальным направлением чтения в данной письменности (во всех видах кириллической и латинской письменности – слева направо), называется прямоходом, обратный – ракоходом или реверсом (справа налево).
Некоторые числа тоже обладают симметрией.
Тропа на лево повела, на порт
Леша на полке клопа нашел
6996
2002
101

Слайд #16
С симметрией мы встречаемся везде: в природе, технике, искусстве, науке. Принципы симметрии играют большую роль в математике и физике, химии и биологии, технике и архитектуре. Законы природы также подчиняются принципам симметрии.
