- Головна
- Готові шкільні презентації
- Презентація на тему «Методи побудови перерізів многогранників»
Презентація на тему «Методи побудови перерізів многогранників»
577
Слайд #1

Слайд #2
Якщо жодна з двох точок не належить площині, а відрізок, що їх сполучає, має з цією площиною спільну точку, то кажуть, що дані точки лежать по різні боки від площини. А якщо принаймні дві точки многогранника лежать по різні боки від площини, кажуть, що площина перетинає многогранник. У цьому разі її називають січною площиною. Фігура, яка складається з усіх точок, спільних для многогранника і січної площини, називається перерізом многогранника даною площиною.
Що таке переріз многогранника?
Що таке переріз многогранника?

Слайд #3
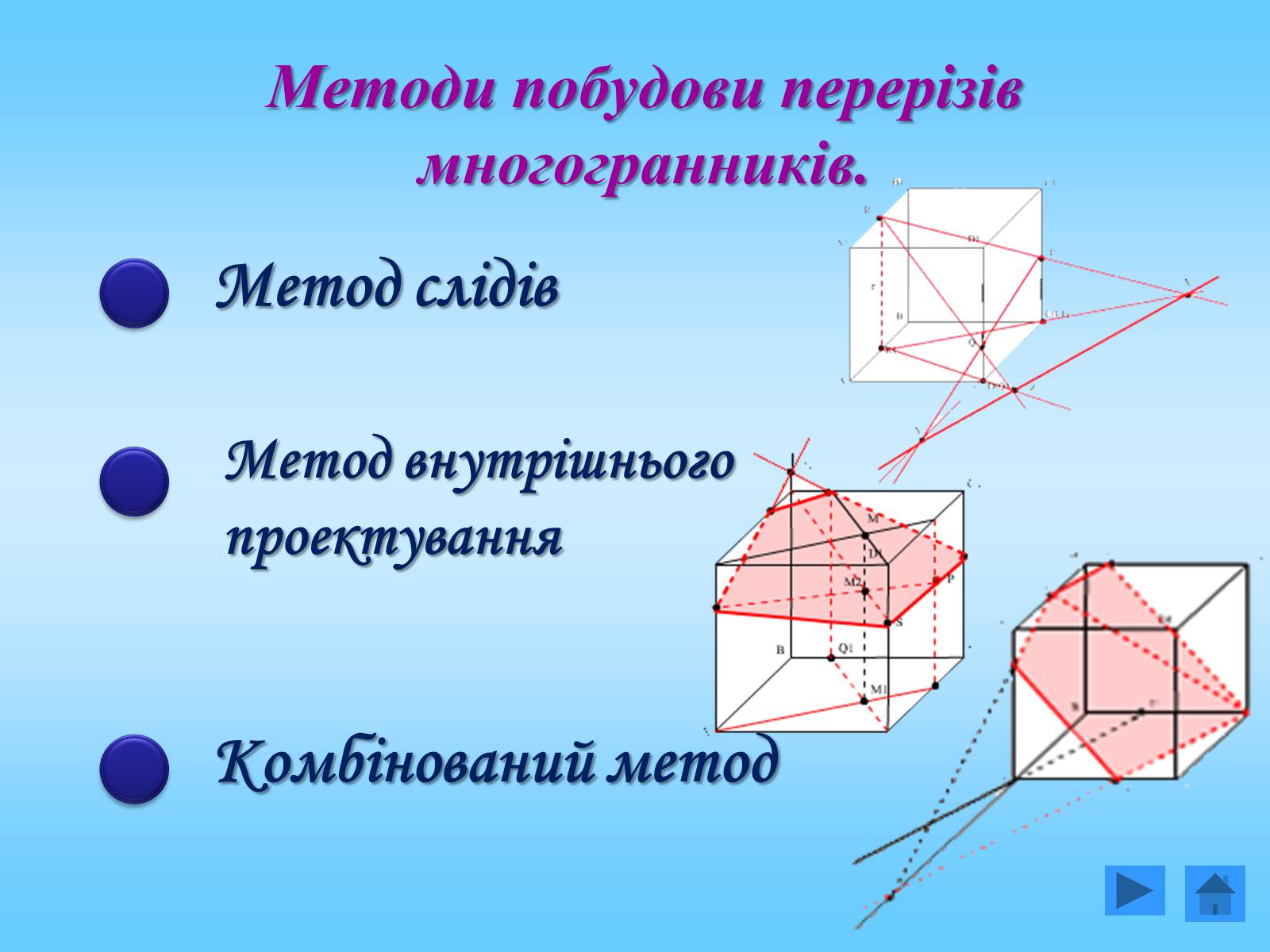
Методи побудови перерізів многогранників.
Метод слідів
Метод внутрішнього проектування
Комбінований метод
Метод слідів
Метод внутрішнього проектування
Комбінований метод
Слайд #4
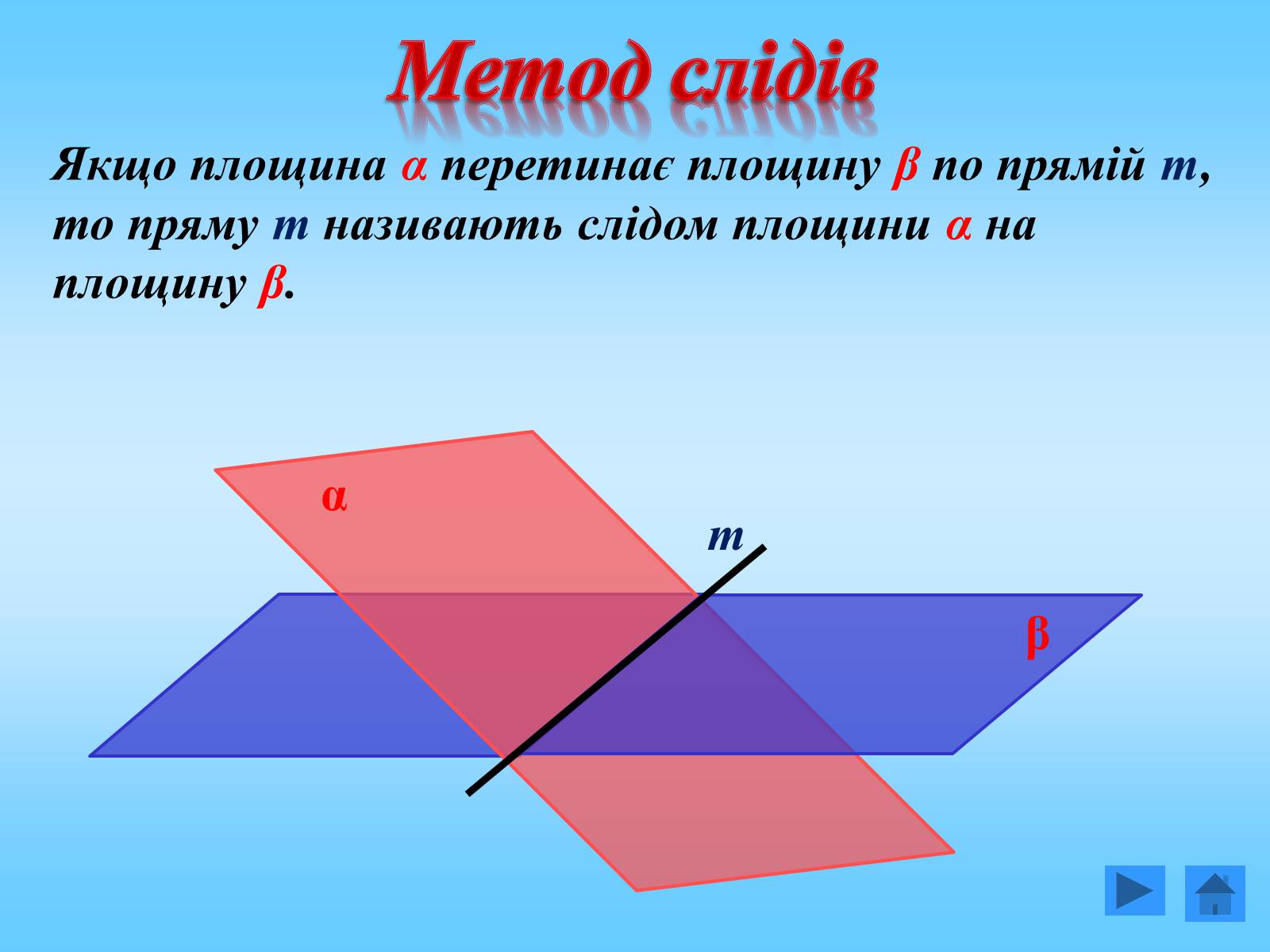
Метод слідів
Якщо площина α перетинає площину β по прямій т, то пряму т називають слідом площини α на площину β.
α
β
т
Якщо площина α перетинає площину β по прямій т, то пряму т називають слідом площини α на площину β.
α
β
т
Слайд #5
Метод слідів
Метод слідів включає три важливих пункти:
Будується лінія перетину (слід) січної площини з площиною основи многогранника.
знаходимо точки перетину січної площини з ребром многогранника.
Будуємо і заштриховуємо переріз.
М
C
B
А
К
Р
Довідка
Метод слідів включає три важливих пункти:
Будується лінія перетину (слід) січної площини з площиною основи многогранника.
знаходимо точки перетину січної площини з ребром многогранника.
Будуємо і заштриховуємо переріз.
М
C
B
А
К
Р
Довідка

Слайд #6
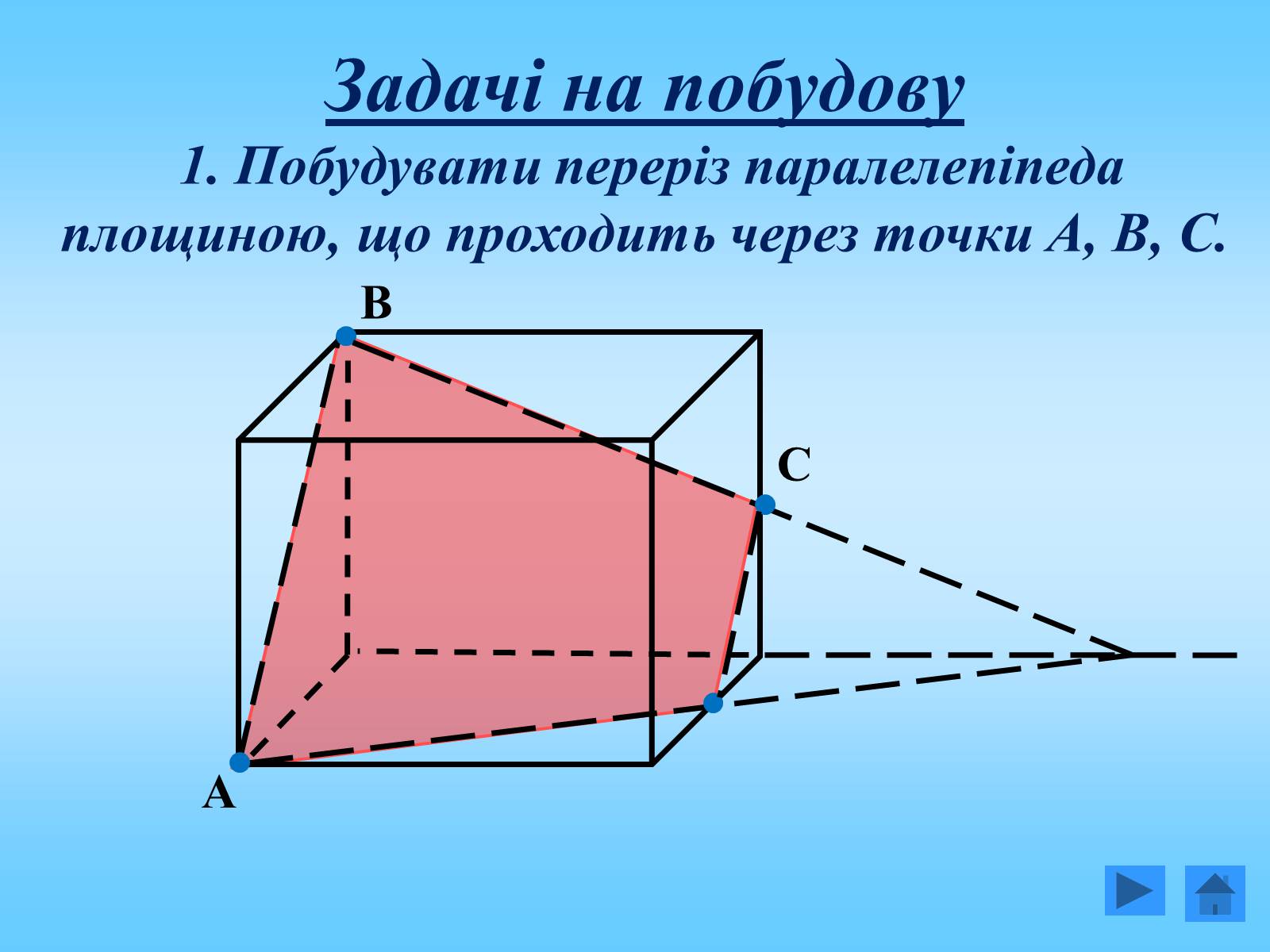
Задачі на побудову
1. Побудувати переріз паралелепіпеда площиною, що проходить через точки А, В, С.
А
С
В
1. Побудувати переріз паралелепіпеда площиною, що проходить через точки А, В, С.
А
С
В
Слайд #7
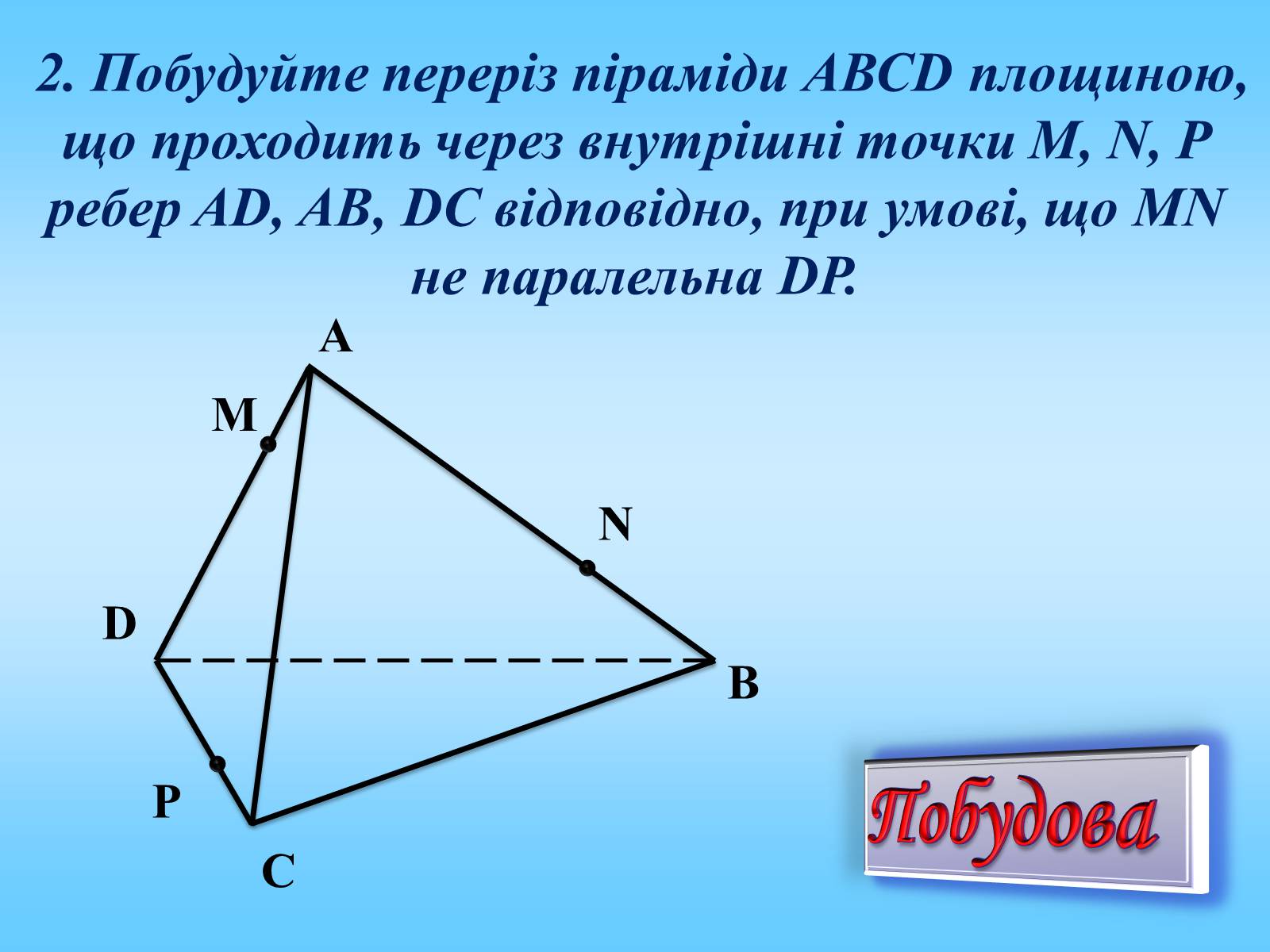
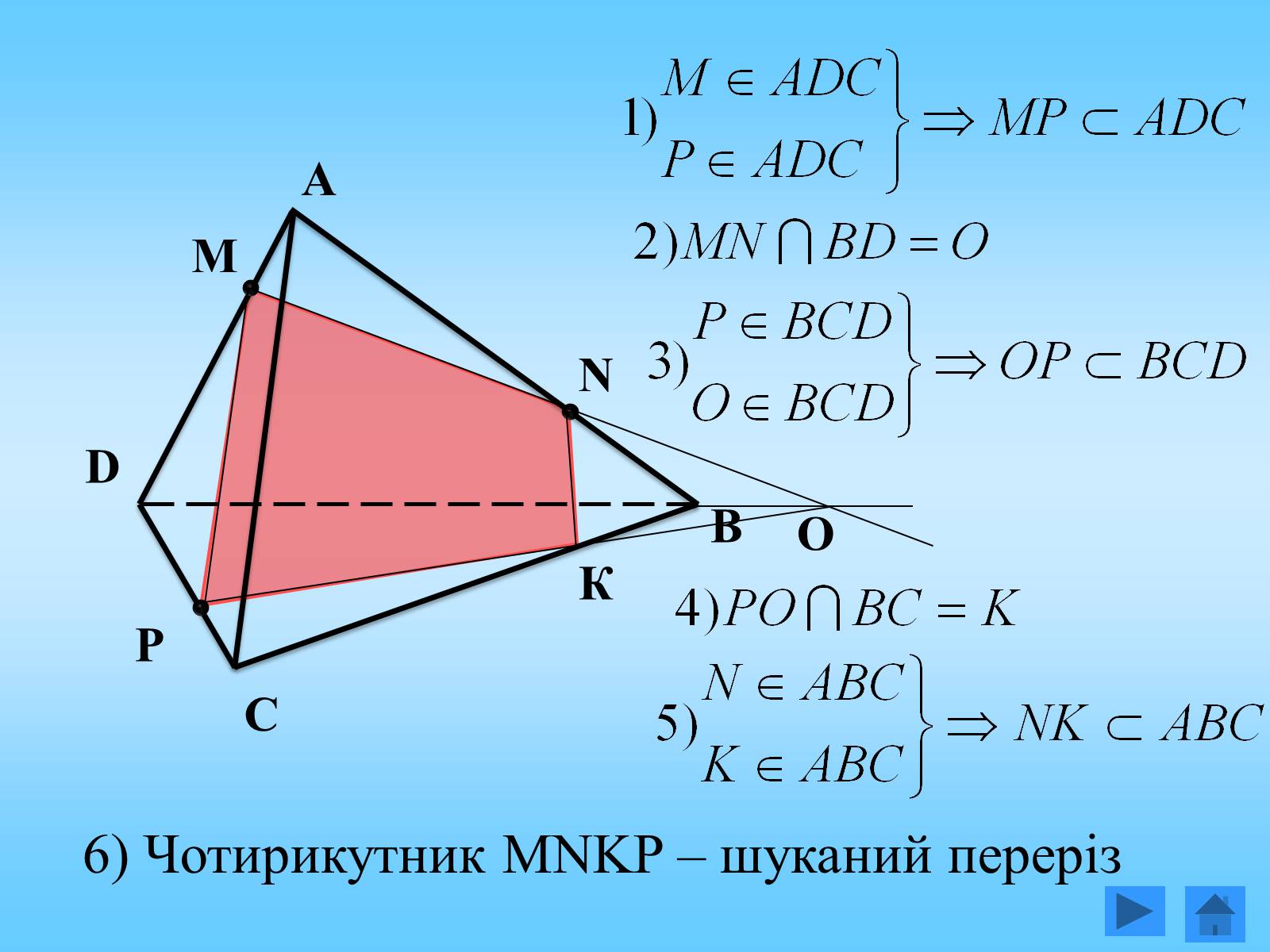
2. Побудуйте переріз піраміди АВСD площиною, що проходить через внутрішні точки M, N, P ребер AD, AB, DC відповідно, при умові, що MN не паралельна DP.
A
P
C
N
M
D
B
Побудова
A
P
C
N
M
D
B
Побудова
Слайд #8
A
P
C
N
M
D
B
О
К
6) Чотирикутник MNKP – шуканий переріз
P
C
N
M
D
B
О
К
6) Чотирикутник MNKP – шуканий переріз
Слайд #9
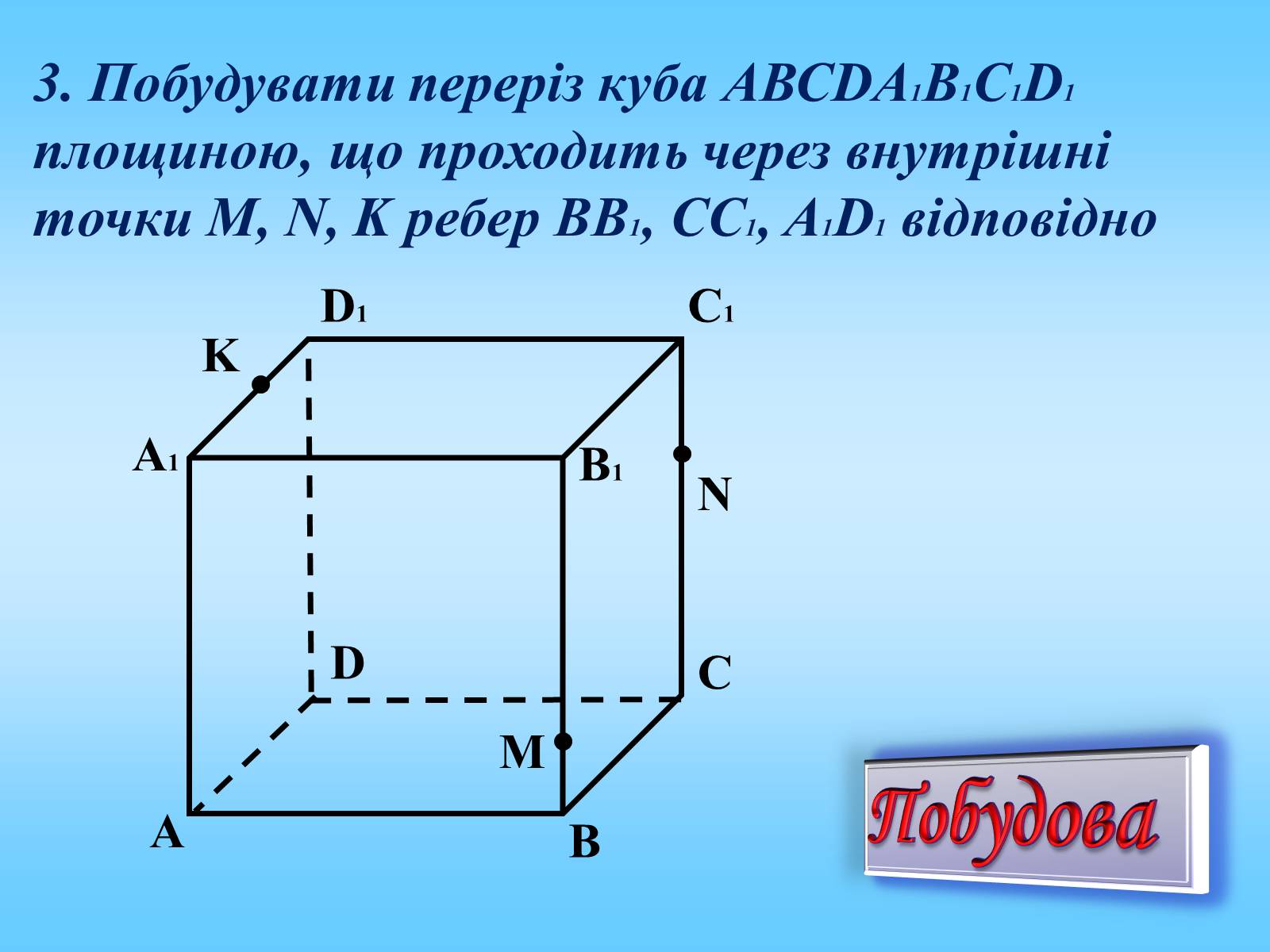
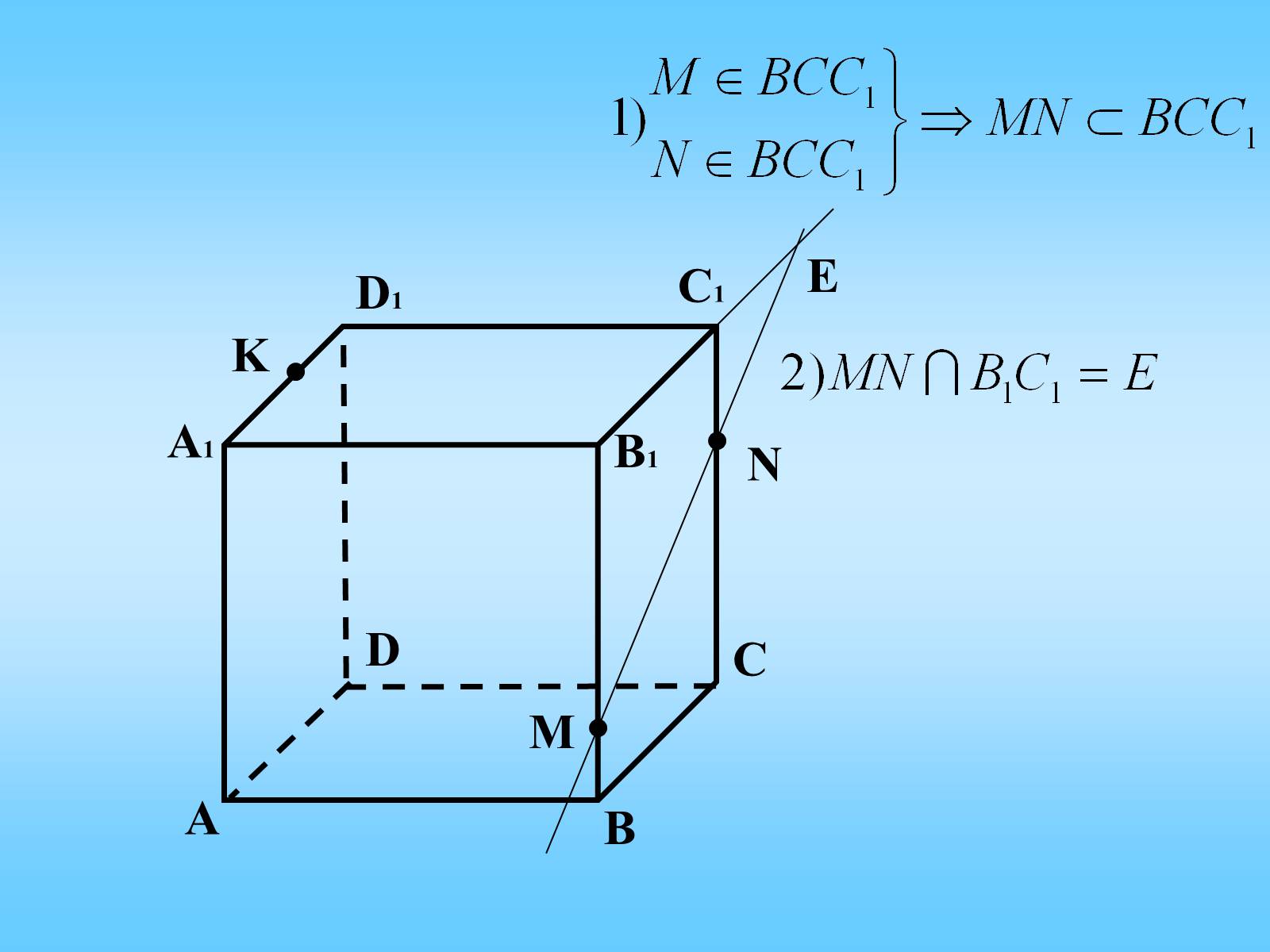
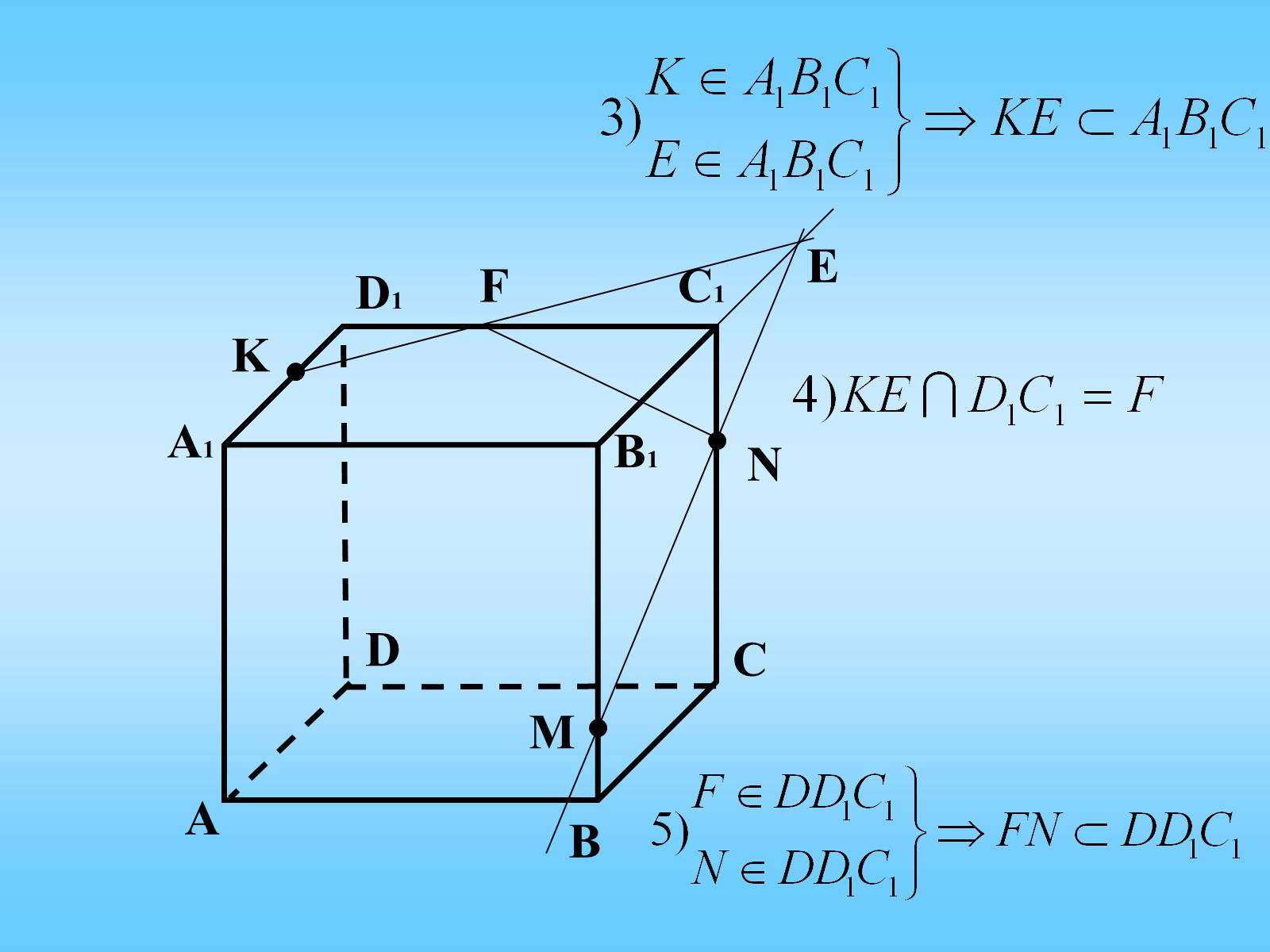
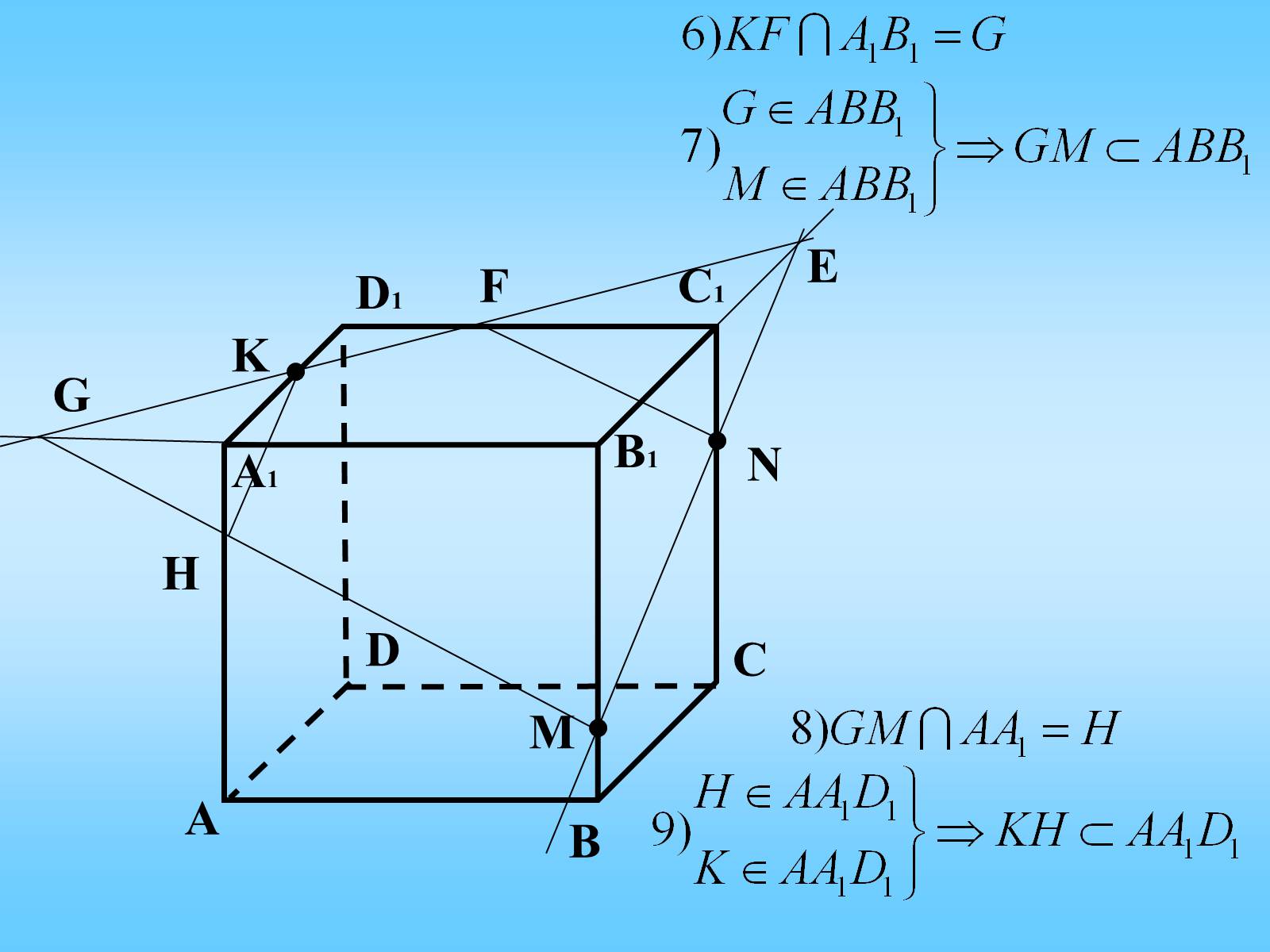
3. Побудувати переріз куба АВСDА1В1С1D1 площиною, що проходить через внутрішні точки M, N, K ребер BB1, CC1, A1D1 відповідно
А
C
B
D
А1
D1
C1
B1
K
N
M
Побудова
А
C
B
D
А1
D1
C1
B1
K
N
M
Побудова
Слайд #10
А
C
B
D
А1
D1
C1
B1
K
N
M
Е
C
B
D
А1
D1
C1
B1
K
N
M
Е
Слайд #11
А
C
B
D
А1
D1
C1
B1
K
N
M
Е
F
C
B
D
А1
D1
C1
B1
K
N
M
Е
F
Слайд #12
А
C
B
D
А1
D1
C1
B1
K
N
M
Е
F
G
H
C
B
D
А1
D1
C1
B1
K
N
M
Е
F
G
H
Слайд #13
А
C
B
D
А1
D1
C1
B1
K
N
M
Е
F
G
H
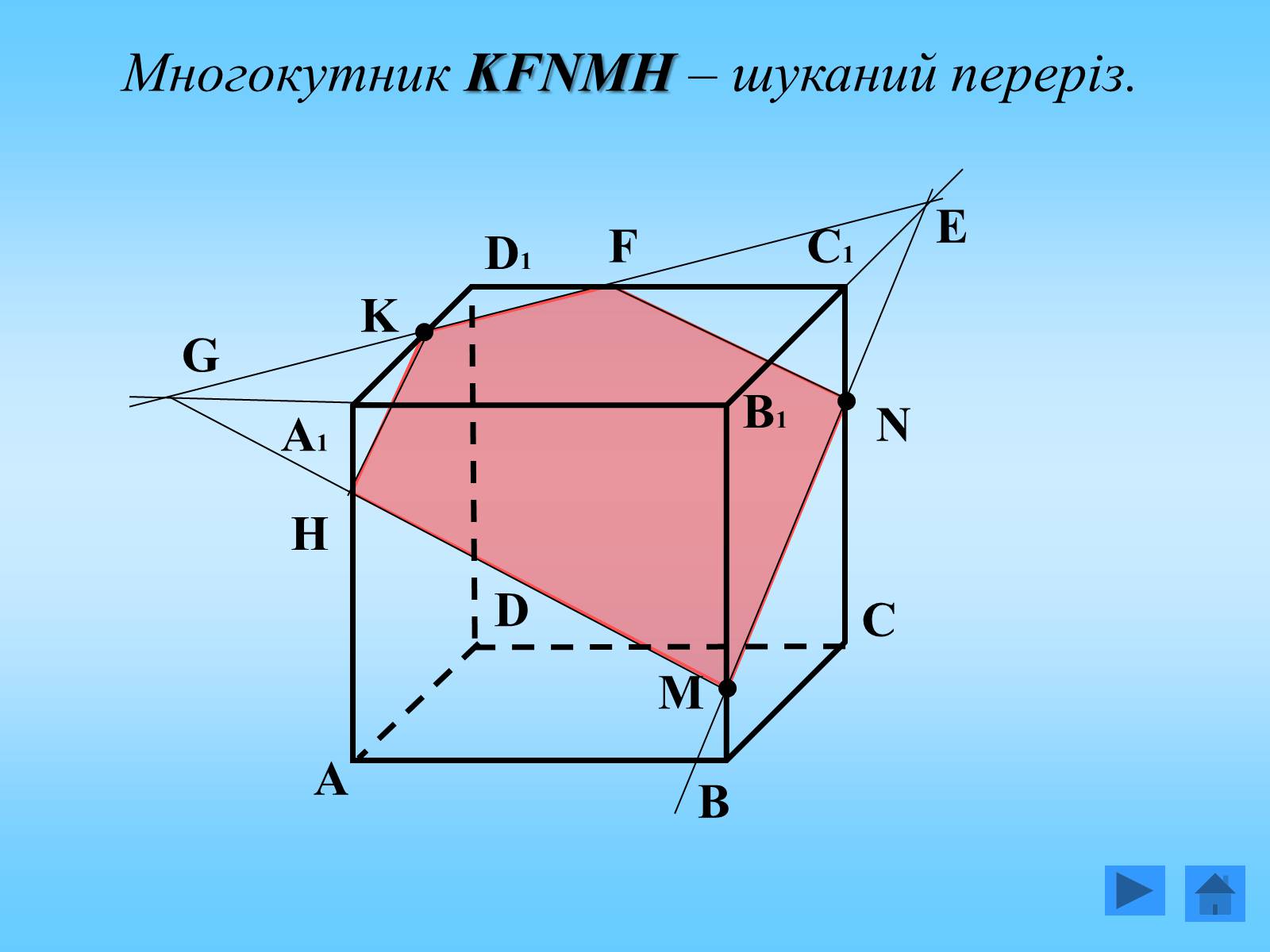
Многокутник KFNMH – шуканий переріз.
C
B
D
А1
D1
C1
B1
K
N
M
Е
F
G
H
Многокутник KFNMH – шуканий переріз.
Слайд #14
M
N
K
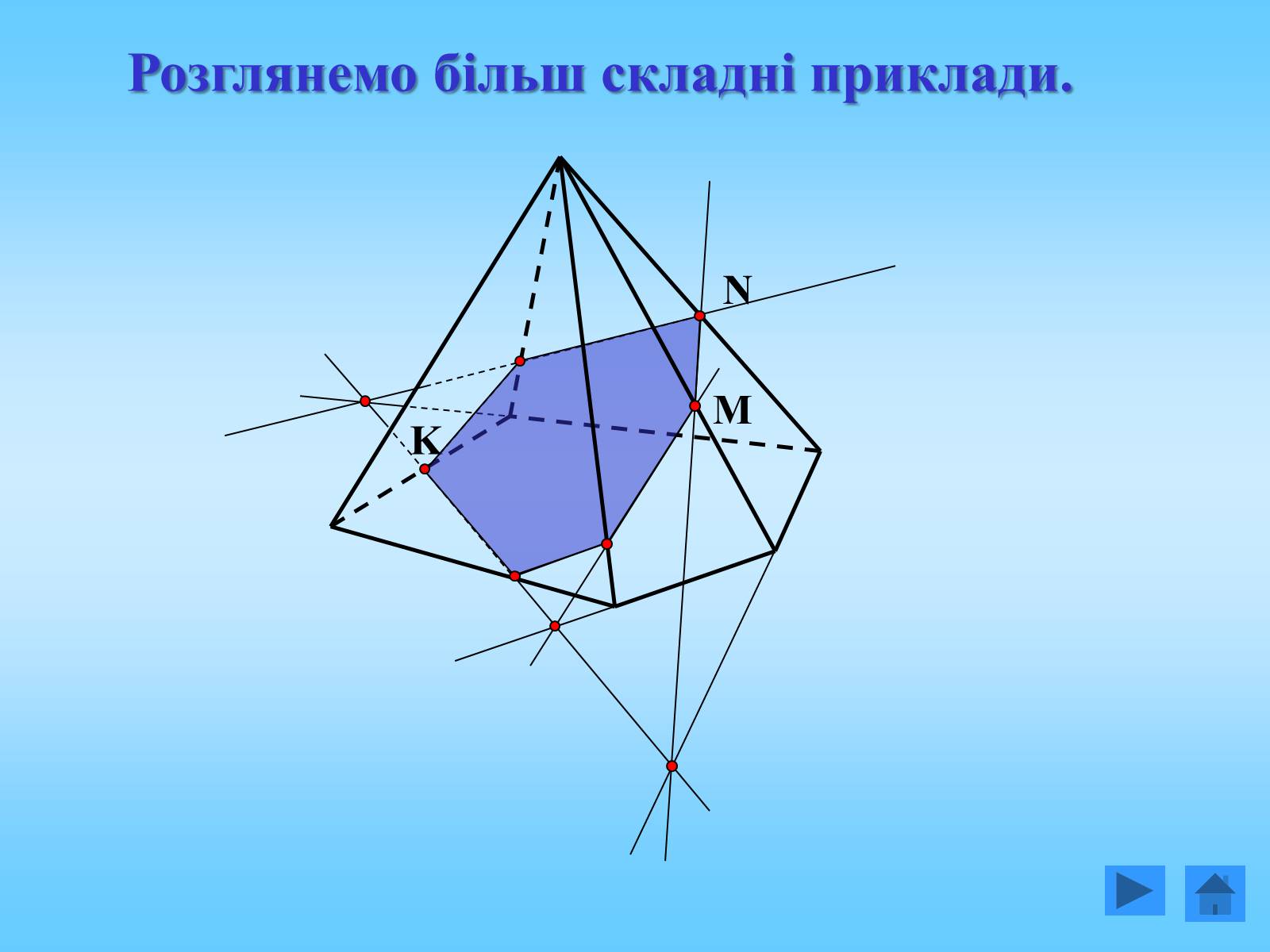
Розглянемо більш складні приклади.
N
K
Розглянемо більш складні приклади.
Слайд #15
M
N
K
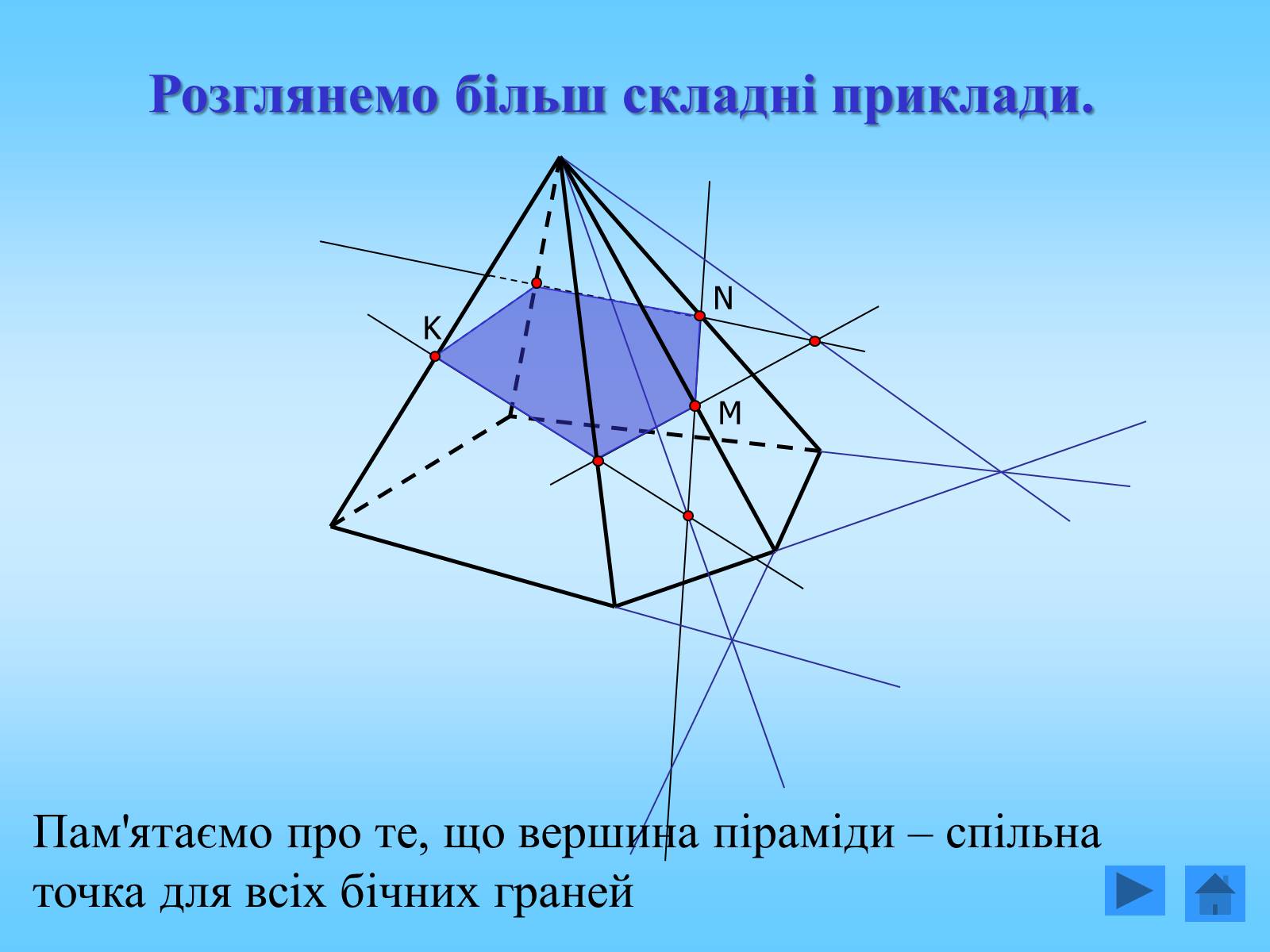
Пам'ятаємо про те, що вершина піраміди – спільна точка для всіх бічних граней
Розглянемо більш складні приклади.
N
K
Пам'ятаємо про те, що вершина піраміди – спільна точка для всіх бічних граней
Розглянемо більш складні приклади.
Слайд #16
K
M
N
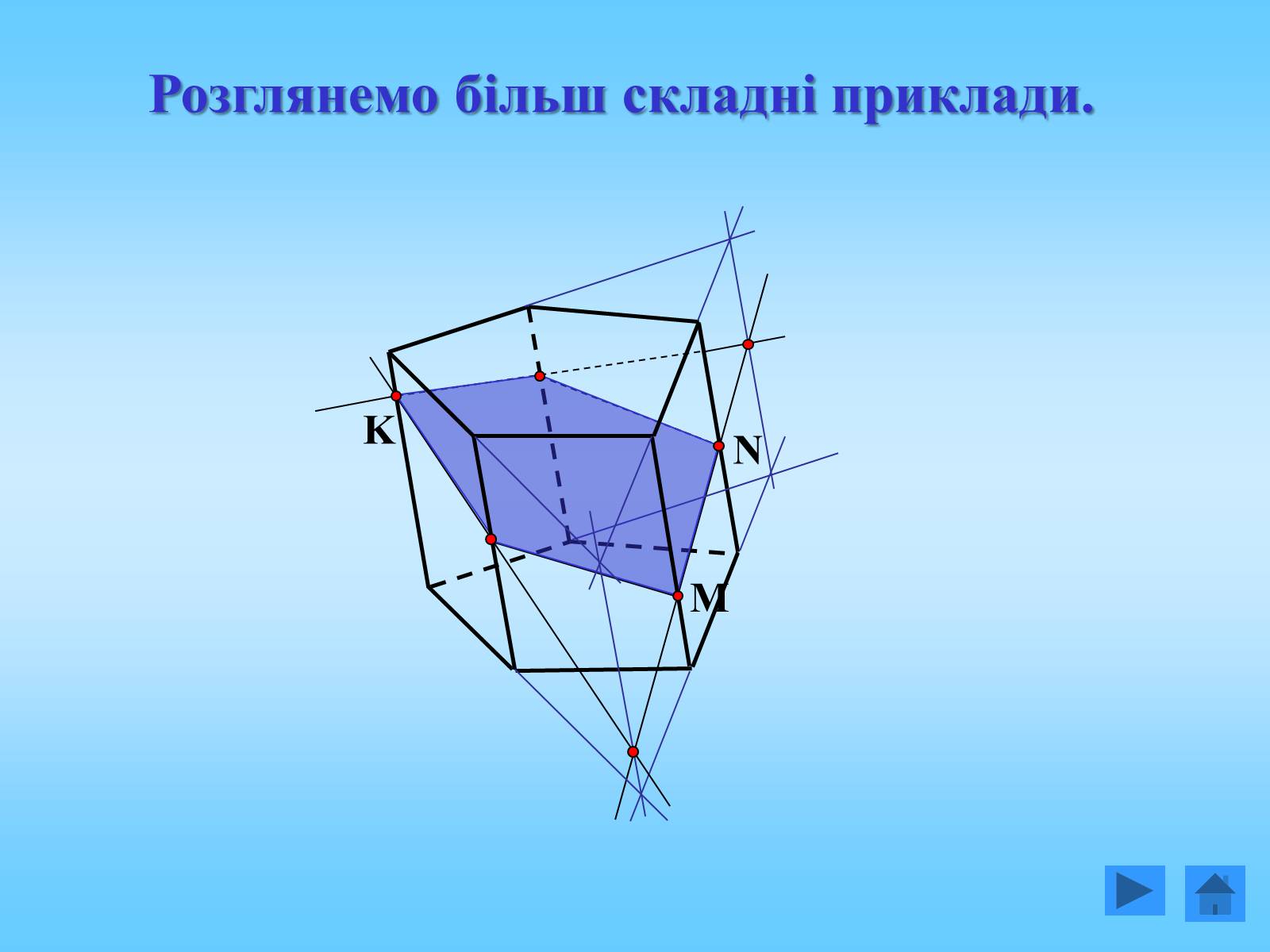
Розглянемо більш складні приклади.
M
N
Розглянемо більш складні приклади.
Слайд #17
M
Метод внутрішнього проектування
X
Y
A
A1
N
M1
N1
T
D1=T1
B
C
D
E
E1
C1
B1
Це метод використовується при побудові перерізів в тих випадках, коли незручно знаходити слід січної площини, наприклад, слід знаходиться дуже далеко від заданої фігури
Метод внутрішнього проектування
X
Y
A
A1
N
M1
N1
T
D1=T1
B
C
D
E
E1
C1
B1
Це метод використовується при побудові перерізів в тих випадках, коли незручно знаходити слід січної площини, наприклад, слід знаходиться дуже далеко від заданої фігури

Слайд #18
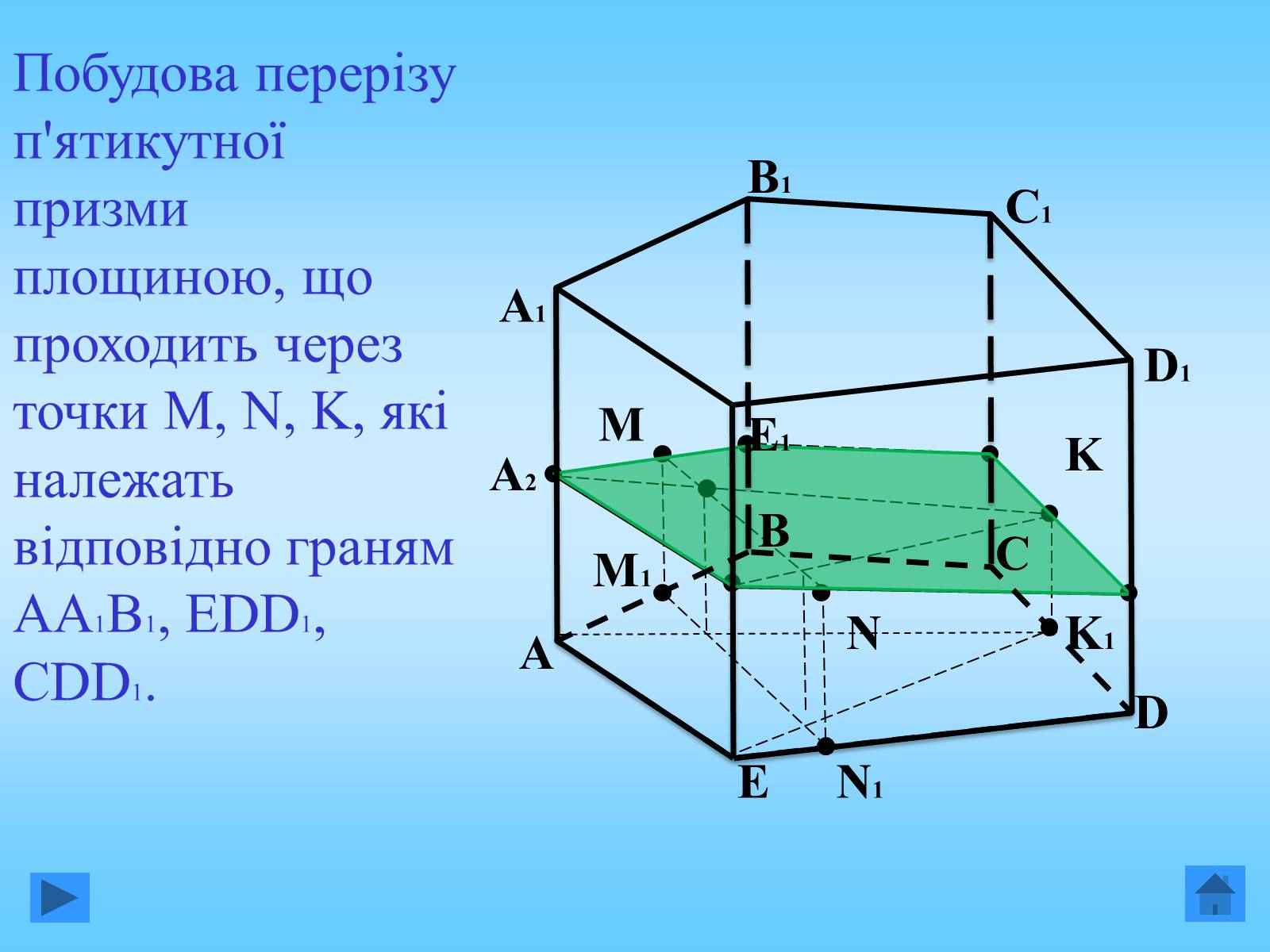
Побудова перерізу п'ятикутної призми площиною, що проходить через точки M, N, K, які належать відповідно граням АА1В1, ЕDD1, CDD1.
A
C
B
M
D
E
A1
C1
B1
D1
E1
K
N
M1
N1
K1
A2
A
C
B
M
D
E
A1
C1
B1
D1
E1
K
N
M1
N1
K1
A2
Слайд #19
Комбінований метод.
При побудові перерізу цим методом на яких етапах побудови використовуються прийоми методу слідів або метода внутрішнього проектування, а на інших етапах використовуються теореми вивченні ще раніше.
При побудові перерізу цим методом на яких етапах побудови використовуються прийоми методу слідів або метода внутрішнього проектування, а на інших етапах використовуються теореми вивченні ще раніше.

Слайд #20
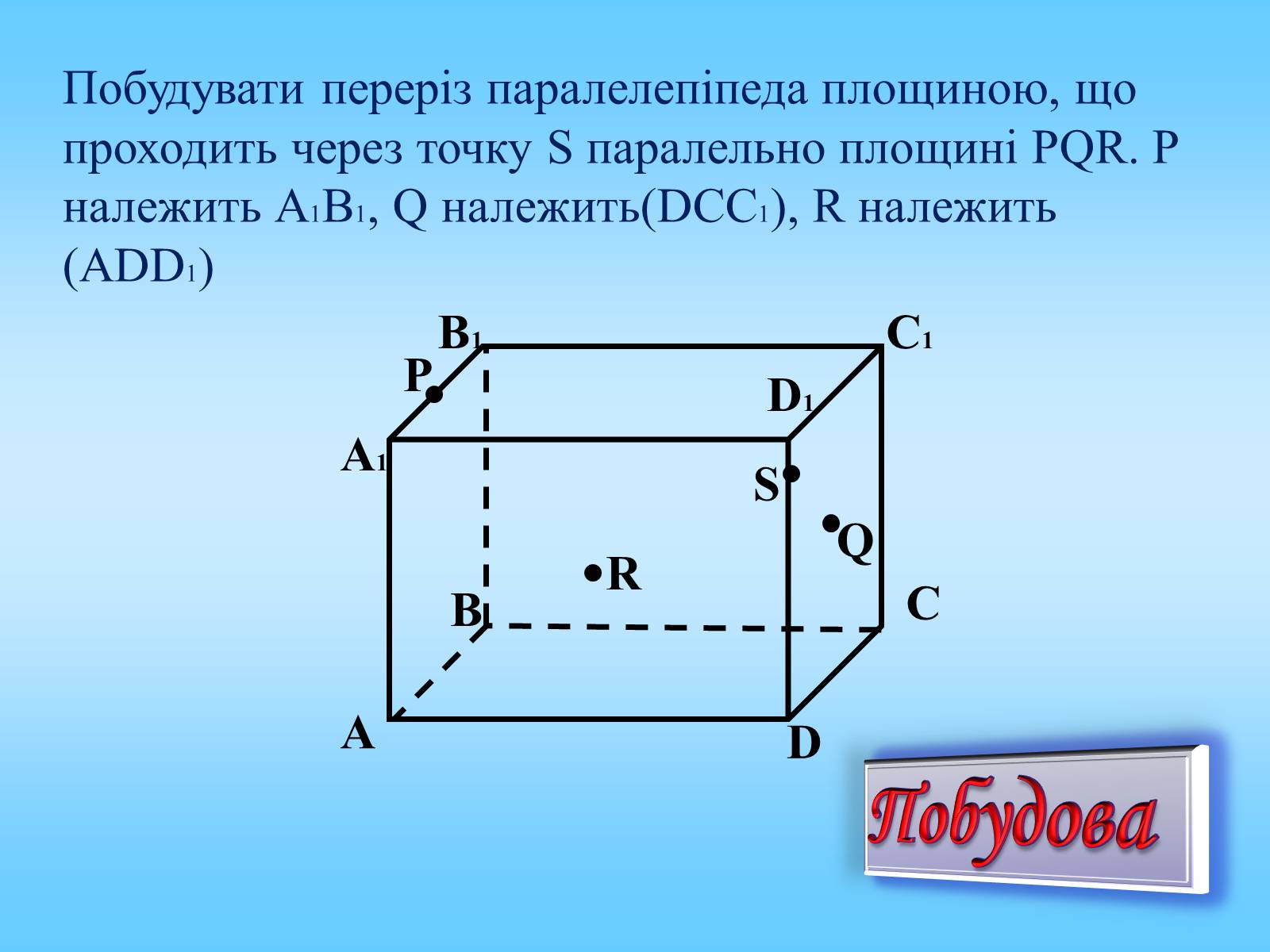
Побудувати переріз паралелепіпеда площиною, що проходить через точку S паралельно площині PQR. P належить А1В1, Q належить(DCC1), R належить (АDD1)
Q
P
R
B
А
D
C
B1
А1
C1
D1
S
Побудова
Q
P
R
B
А
D
C
B1
А1
C1
D1
S
Побудова
Слайд #21
B
А
D
C
B1
А1
C1
D1
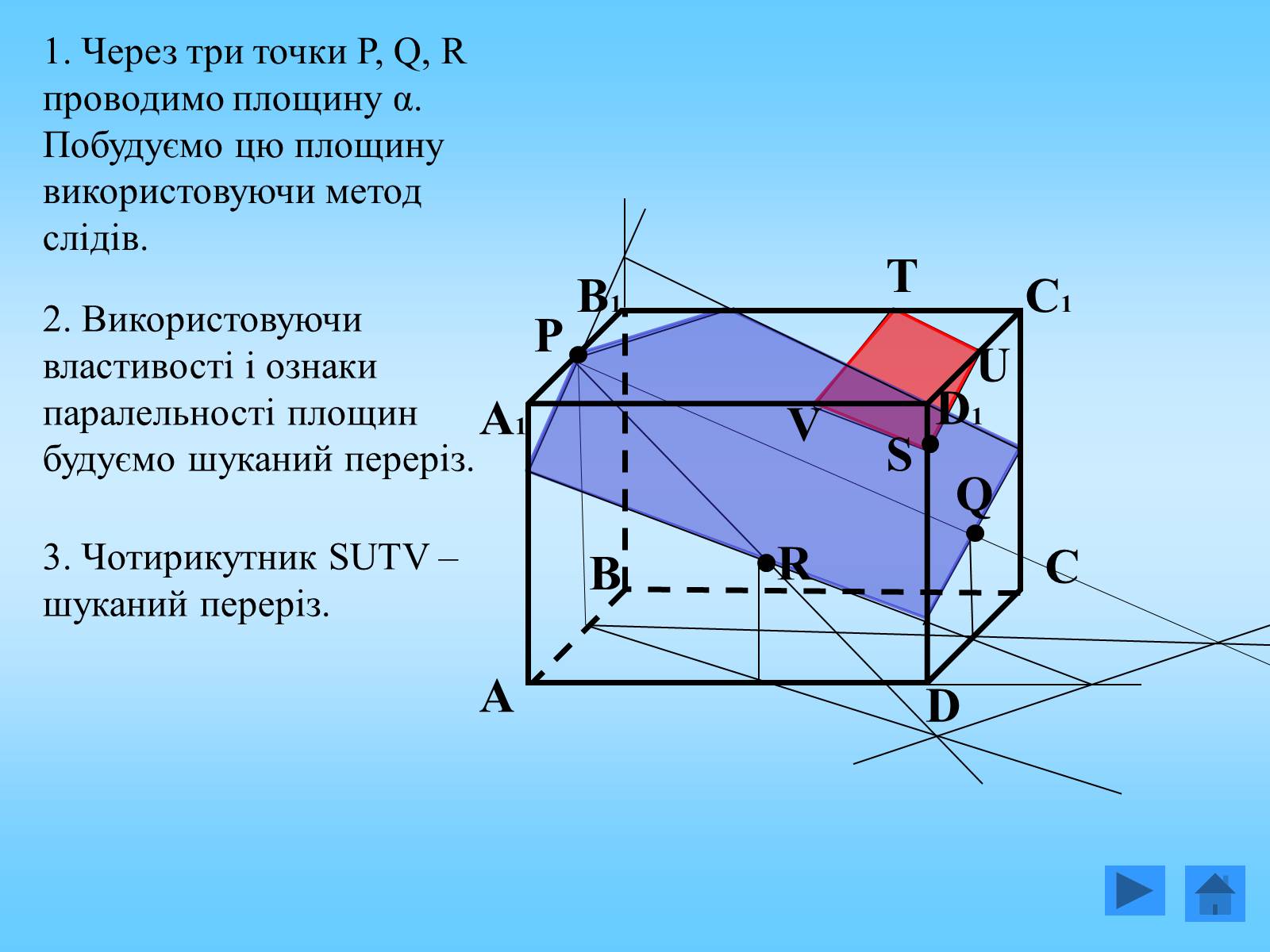
1. Через три точки P, Q, R проводимо площину α. Побудуємо цю площину використовуючи метод слідів.
Q
P
R
S
2. Використовуючи властивості і ознаки паралельності площин будуємо шуканий переріз.
V
T
U
3. Чотирикутник SUTV – шуканий переріз.
А
D
C
B1
А1
C1
D1
1. Через три точки P, Q, R проводимо площину α. Побудуємо цю площину використовуючи метод слідів.
Q
P
R
S
2. Використовуючи властивості і ознаки паралельності площин будуємо шуканий переріз.
V
T
U
3. Чотирикутник SUTV – шуканий переріз.
Слайд #22
Довідковий матеріал.
Аксіома 1. Через будь-які три точки, що не лежать на одній прямій можна провести площину і до того ж тільки одну;
Аксіома 2. Якщо дві точки прямої належать площині, то всі точки даної прямої належать площині;
Аксіома 3. Якщо дві площини мають спільну точку, то вони мають спільну пряму на якій лежать спільні точки цих площин;
Наслідки з аксіом:
Через пряму і точку, що не належить даній прямій можна провести площину і до того ж тільки одну;
Через дві прямі, що перетинаються можна провести площину і до того ж тільки одну.
Теорема (ознака паралельності двох площин). Якщо дві прямі, що перетинаються однієї площини відповідно паралельні двом прямим, що перетинаються іншої площини, то ці площини паралельні;
Теорема (властивість паралельних площин). Якщо дві паралельні площини перетнуто третьою, то лінії їх перетину паралельні;
Теорема (ознака паралельності прямої і площини). Якщо пряма, що не належить даній площині, паралельна будь-які прямій цієї площини, то вона паралельна і даній площині.
Аксіома 1. Через будь-які три точки, що не лежать на одній прямій можна провести площину і до того ж тільки одну;
Аксіома 2. Якщо дві точки прямої належать площині, то всі точки даної прямої належать площині;
Аксіома 3. Якщо дві площини мають спільну точку, то вони мають спільну пряму на якій лежать спільні точки цих площин;
Наслідки з аксіом:
Через пряму і точку, що не належить даній прямій можна провести площину і до того ж тільки одну;
Через дві прямі, що перетинаються можна провести площину і до того ж тільки одну.
Теорема (ознака паралельності двох площин). Якщо дві прямі, що перетинаються однієї площини відповідно паралельні двом прямим, що перетинаються іншої площини, то ці площини паралельні;
Теорема (властивість паралельних площин). Якщо дві паралельні площини перетнуто третьою, то лінії їх перетину паралельні;
Теорема (ознака паралельності прямої і площини). Якщо пряма, що не належить даній площині, паралельна будь-які прямій цієї площини, то вона паралельна і даній площині.

Слайд #23
Література.
Е.К.Лейнартас “Математика. Перерізи многогранників”, Красноярск, 2006
Г. П. Бевз, В. Г. Бевз, Н. Г. Владімірова, В. М. Владіміров “Геометрія. Профільний рівень”, Київ 2010
http://www.freeware.ru/program_prog_id_1536.html (програма, для побудови перерізів основних просторових фігур)
http://mail.spb.fio.ru/archive/group14/c4wu5/tityl.html
Е.К.Лейнартас “Математика. Перерізи многогранників”, Красноярск, 2006
Г. П. Бевз, В. Г. Бевз, Н. Г. Владімірова, В. М. Владіміров “Геометрія. Профільний рівень”, Київ 2010
http://www.freeware.ru/program_prog_id_1536.html (програма, для побудови перерізів основних просторових фігур)
http://mail.spb.fio.ru/archive/group14/c4wu5/tityl.html
