- Головна
- Готові шкільні презентації
- Презентація на тему «Перетворення простору»
Презентація на тему «Перетворення простору»
1256
Слайд #1
Перетворення простору
Підготувала:Черних Аліна 11-А клас
Підготувала:Черних Аліна 11-А клас

Слайд #2
Рух
Рухом називається перетворення, при якому зберігаються відстані між точками.
Властивості руху в просторі:
Прямі переходять у прямі, півпрямі — у півпрямі, відрізки — у відрізки, кути між півпрямими зберігаються, площина переходить у площину.
Зразки рухів у просторі:
Симетрія відносно точки; симетрія відносно прямої; симетрія відносно площини (аналогічна симетрії відносно прямої).
Рухом називається перетворення, при якому зберігаються відстані між точками.
Властивості руху в просторі:
Прямі переходять у прямі, півпрямі — у півпрямі, відрізки — у відрізки, кути між півпрямими зберігаються, площина переходить у площину.
Зразки рухів у просторі:
Симетрія відносно точки; симетрія відносно прямої; симетрія відносно площини (аналогічна симетрії відносно прямої).

Слайд #3
Симетрія
Симетрія досить поширена у природі.Її можна спостерігати у формі листків,квіток,розташуванню органів тварин,також вона широко використовується в будівництві та техніці. Перетворення симетрії у просторі підлягає певним закономірностям, які можна використати для розв'язування практичних задач.
Симетрія досить поширена у природі.Її можна спостерігати у формі листків,квіток,розташуванню органів тварин,також вона широко використовується в будівництві та техніці. Перетворення симетрії у просторі підлягає певним закономірностям, які можна використати для розв'язування практичних задач.

Слайд #4
Симетрія у геометрії
Геометрична фігура симетрична, якщо існують перетворення, при яких її точки змінюють своє розташування на площині або в просторі, однак фігура накладається сама на себе. Якщо частини такої фігури накладаються на інші частини, то ці частини називають симетричними між собою. В залежності від типу перетворень розрізняють різні види симетрії.
Дзеркальна симетрія
Дзеркальною називається симетрія щодо операції відбиття відносно площини або, в планіметрії, лінії. У планіметрії цей тип симетрії називають осьовою.
Геометрична фігура симетрична, якщо існують перетворення, при яких її точки змінюють своє розташування на площині або в просторі, однак фігура накладається сама на себе. Якщо частини такої фігури накладаються на інші частини, то ці частини називають симетричними між собою. В залежності від типу перетворень розрізняють різні види симетрії.
Дзеркальна симетрія
Дзеркальною називається симетрія щодо операції відбиття відносно площини або, в планіметрії, лінії. У планіметрії цей тип симетрії називають осьовою.

Слайд #5
Приклад дзеркальної симетрії

Слайд #6
Центральна симетрія
Геометрична фігура має центральну симетрію щодо певної точки, яка називається центром симетрії, якщо для будь-якої точки фігури існує інша точка, розташована на лінії, що сполучає дану точку з центром, з іншого боку від центра на однаковій відстані.
У планіметрії, для двовимірної фігури, центральна симетрія еквівалентна існуванню осі обертання другого порядку, тобто симетрії щодо повороту на 180°. У стереометрії, для тривимірної фігури, центральна симетрія є симетрією щодо складеної операції — повороту на 180° щодо довільної осі, яка проходить через центр симетрії, та дзеркального відбиття в площині, перпендикулярній цій осі.
Геометрична фігура має центральну симетрію щодо певної точки, яка називається центром симетрії, якщо для будь-якої точки фігури існує інша точка, розташована на лінії, що сполучає дану точку з центром, з іншого боку від центра на однаковій відстані.
У планіметрії, для двовимірної фігури, центральна симетрія еквівалентна існуванню осі обертання другого порядку, тобто симетрії щодо повороту на 180°. У стереометрії, для тривимірної фігури, центральна симетрія є симетрією щодо складеної операції — повороту на 180° щодо довільної осі, яка проходить через центр симетрії, та дзеркального відбиття в площині, перпендикулярній цій осі.

Слайд #7
Трансляційна симетрія
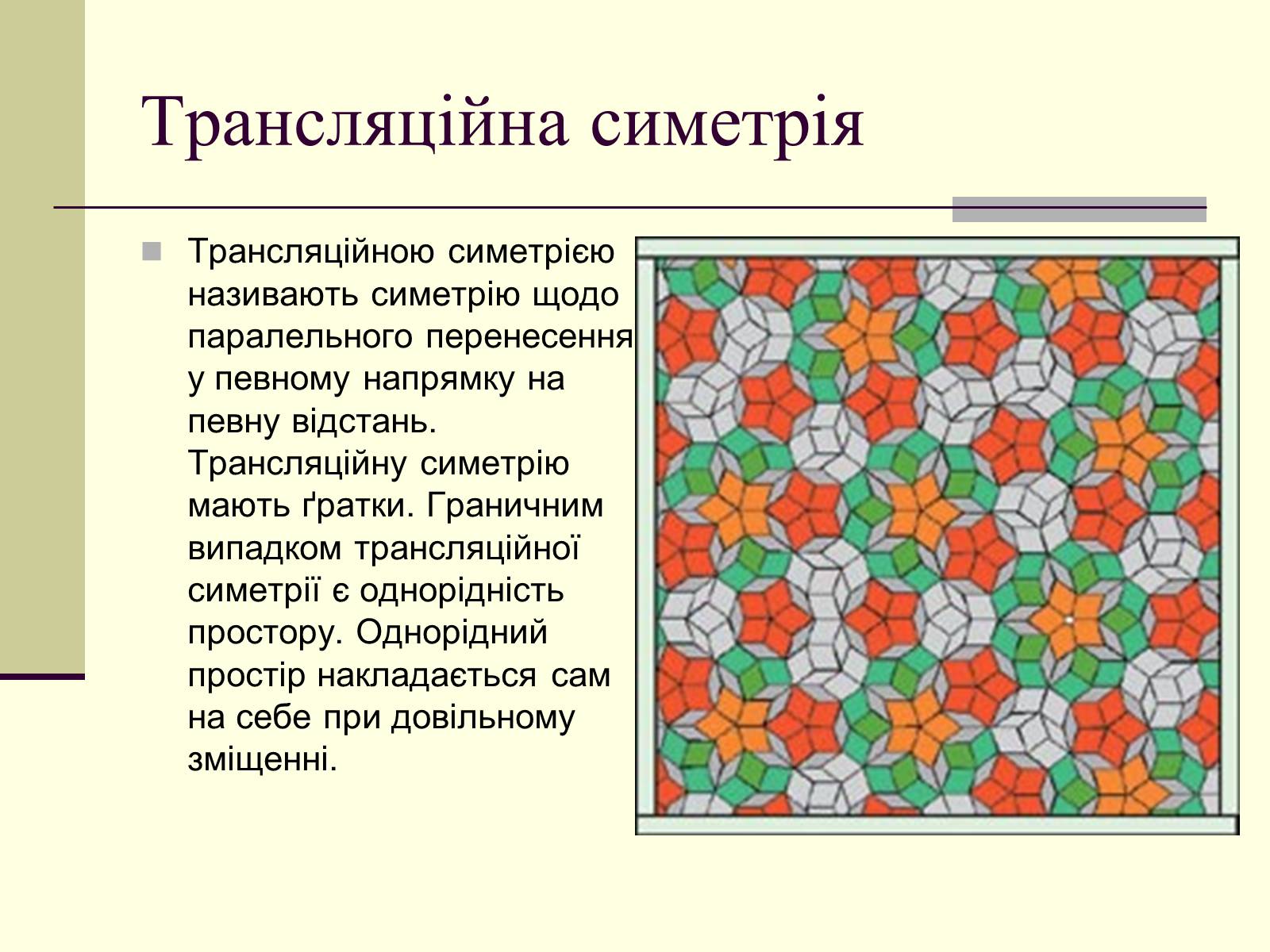
Трансляційною симетрією називають симетрію щодо паралельного перенесення у певному напрямку на певну відстань. Трансляційну симетрію мають ґратки. Граничним випадком трансляційної симетрії є однорідність простору. Однорідний простір накладається сам на себе при довільному зміщенні.
Трансляційною симетрією називають симетрію щодо паралельного перенесення у певному напрямку на певну відстань. Трансляційну симетрію мають ґратки. Граничним випадком трансляційної симетрії є однорідність простору. Однорідний простір накладається сам на себе при довільному зміщенні.
Слайд #8
Симетрія в біології
Симетричність — найважливіша характеристика будови тіла тварин, це властивість організму складатися із частин, які дзеркально повторюються і розташовані уздовж уявної площини, що проходить крізь тіло. Тип симетрії визначає не лише загальну будову тіла, а можливість розвитку систем органів тварини. Якщо тіло тварини можна уявно поділити на дві половини, праву та ліву, то таку тварину називають двобічносиметричною. Цей тип симетрії властивий переважній більшості видів тварин, а також людині. Якщо тіло тварини можна уявно поділити не однією, а кількома площинами симетрії (уявними дзеркалами) на рівні частини, то таку тварину називають радіально-симетричною. Цей тип симетрії трапляється значно рідше. Радіально-симетричні тварини мають простішу будову, пересуваються повільно — повзанням. У таких тварин відсутні високорозвинені органи чуття та складні системи органів. Незначна їх рухливість, пасивний спосіб життя не сприяють розвитку систем органів і вдосконаленню нервової регуляції організму.
Симетричність — найважливіша характеристика будови тіла тварин, це властивість організму складатися із частин, які дзеркально повторюються і розташовані уздовж уявної площини, що проходить крізь тіло. Тип симетрії визначає не лише загальну будову тіла, а можливість розвитку систем органів тварини. Якщо тіло тварини можна уявно поділити на дві половини, праву та ліву, то таку тварину називають двобічносиметричною. Цей тип симетрії властивий переважній більшості видів тварин, а також людині. Якщо тіло тварини можна уявно поділити не однією, а кількома площинами симетрії (уявними дзеркалами) на рівні частини, то таку тварину називають радіально-симетричною. Цей тип симетрії трапляється значно рідше. Радіально-симетричні тварини мають простішу будову, пересуваються повільно — повзанням. У таких тварин відсутні високорозвинені органи чуття та складні системи органів. Незначна їх рухливість, пасивний спосіб життя не сприяють розвитку систем органів і вдосконаленню нервової регуляції організму.

Слайд #9
Приклади симетрії в біології

Слайд #10
Обертання
Обертання - вид руху, при якому одна точка механічної системи, що називається центром обертання, залишається непорушною.
Для замкнутої механічної системи, для якої виконується закон збереження імпульсу, будь-який рух можна розділити на поступальний рух центра інерції і обертання навколо цього центру.
При обертанні замкнутої механічної системи виконується закон збереження моменту імпульсу.
В загальному випадку незамкненої механічної системи центр обертання може не збігатися з центром інерції. Центр обертання в багатьох випадках фіксований накладеними на механічну систему зовнішніми в'язями. Так, наприклад, при обертанні дзиґи центр обертання - точка опори.
Обертання - вид руху, при якому одна точка механічної системи, що називається центром обертання, залишається непорушною.
Для замкнутої механічної системи, для якої виконується закон збереження імпульсу, будь-який рух можна розділити на поступальний рух центра інерції і обертання навколо цього центру.
При обертанні замкнутої механічної системи виконується закон збереження моменту імпульсу.
В загальному випадку незамкненої механічної системи центр обертання може не збігатися з центром інерції. Центр обертання в багатьох випадках фіксований накладеними на механічну систему зовнішніми в'язями. Так, наприклад, при обертанні дзиґи центр обертання - точка опори.

Слайд #11
Паралельне перенесення
Паралельне перенесення та його властивості
Перетворення фігури F, при якому довільна її точка з координатами переходить у точку , де a і b — одні й ті самі для всіх точок, називається паралельним перенесенням.
Теорема. Паралельне перенесення є рухом.
При паралельному перенесенні пряма переходить у паралельну пряму (або в себе)
Паралельне перенесення та його властивості
Перетворення фігури F, при якому довільна її точка з координатами переходить у точку , де a і b — одні й ті самі для всіх точок, називається паралельним перенесенням.
Теорема. Паралельне перенесення є рухом.
При паралельному перенесенні пряма переходить у паралельну пряму (або в себе)
