Презентація на тему «Формули скороченого множення» (варіант 3)
308
Слайд #1
Формули скороченого множення.
Автор: Плахотна С.Б., вчитель математики та астрономії
Автор: Плахотна С.Б., вчитель математики та астрономії
Слайд #2
Історичний екскурс.
Число - аріфмос (грец.)
Геометрія - гео - земля (грец.), метрео - міряю (грец.)
Аль джебр - відновлення (араб.)
Число - аріфмос (грец.)
Геометрія - гео - земля (грец.), метрео - міряю (грец.)
Аль джебр - відновлення (араб.)
Слайд #3
Евклід «Начала».
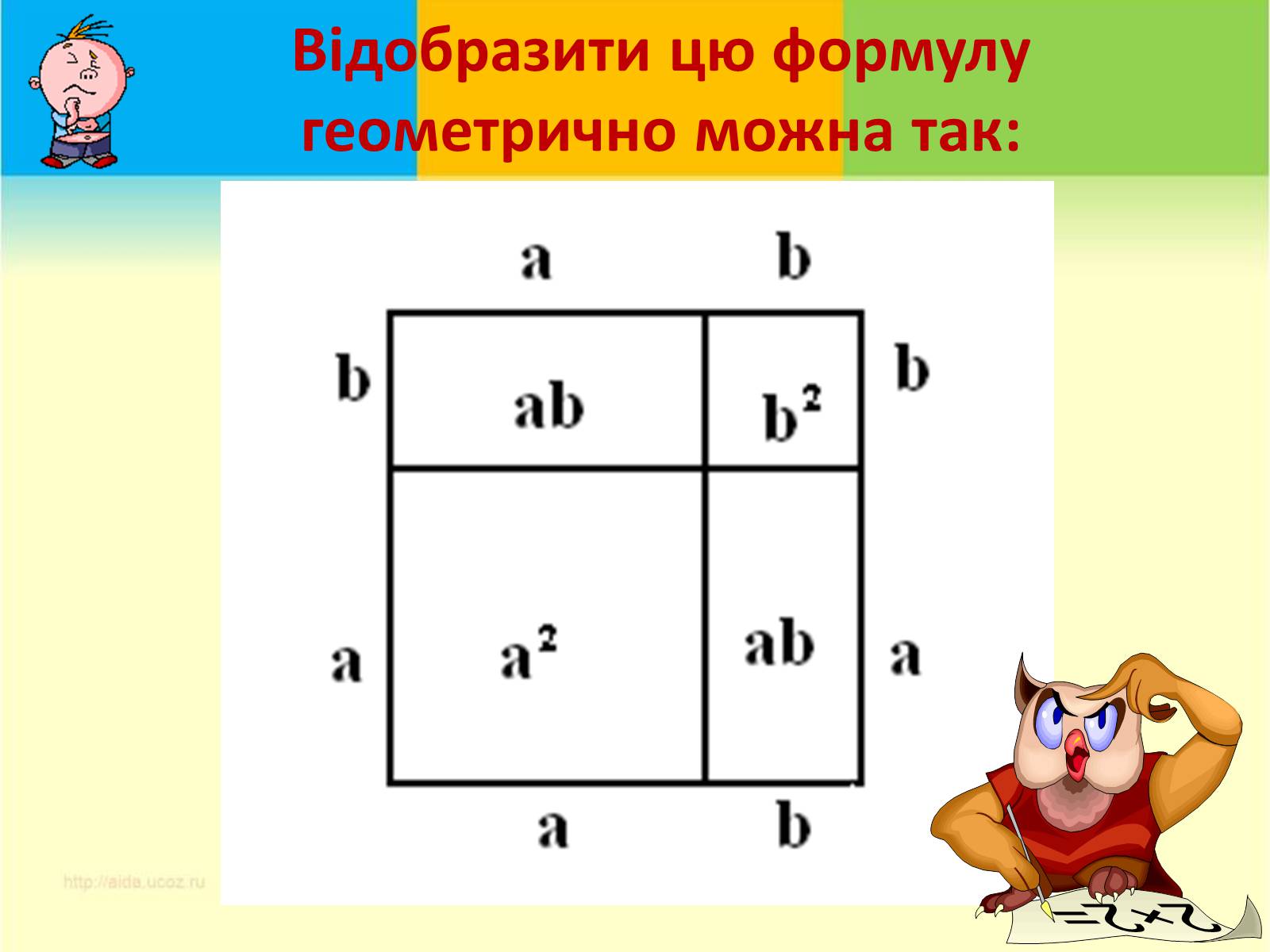
«Якщо відрізок як-небудь розбити на два відрізки, то площа квадрата, побудованого на всьому відрізку, дорівнює сумі площ квадратів, побудованих на кожному з двох відрізків, і подвоєній площі прямокутника, сторонами якого служать ці два відрізки.»
Суть цієї фрази у формулі:
(а + b)2 = a2 + 2ab + b2
«Якщо відрізок як-небудь розбити на два відрізки, то площа квадрата, побудованого на всьому відрізку, дорівнює сумі площ квадратів, побудованих на кожному з двох відрізків, і подвоєній площі прямокутника, сторонами якого служать ці два відрізки.»
Суть цієї фрази у формулі:
(а + b)2 = a2 + 2ab + b2
Слайд #4
Відобразити цю формулу геометрично можна так:
Слайд #5
Квадрат суми (різниці) двох виразів :.
(a±b)2=a2±2ab+b2
a2-b2=(a-b)(а+b)
Різниця квадратів двох
виразів:
(a±b)2=a2±2ab+b2
a2-b2=(a-b)(а+b)
Різниця квадратів двох
виразів:
Слайд #6
Сума (різниця) кубів двох виразів:.
(a±b)3 = a3 ± 3 a2b + 3 ab2 ± b3
Куб суми (різниці) двох
виразів:
(a±b)3 = a3 ± 3 a2b + 3 ab2 ± b3
Куб суми (різниці) двох
виразів:
Слайд #7
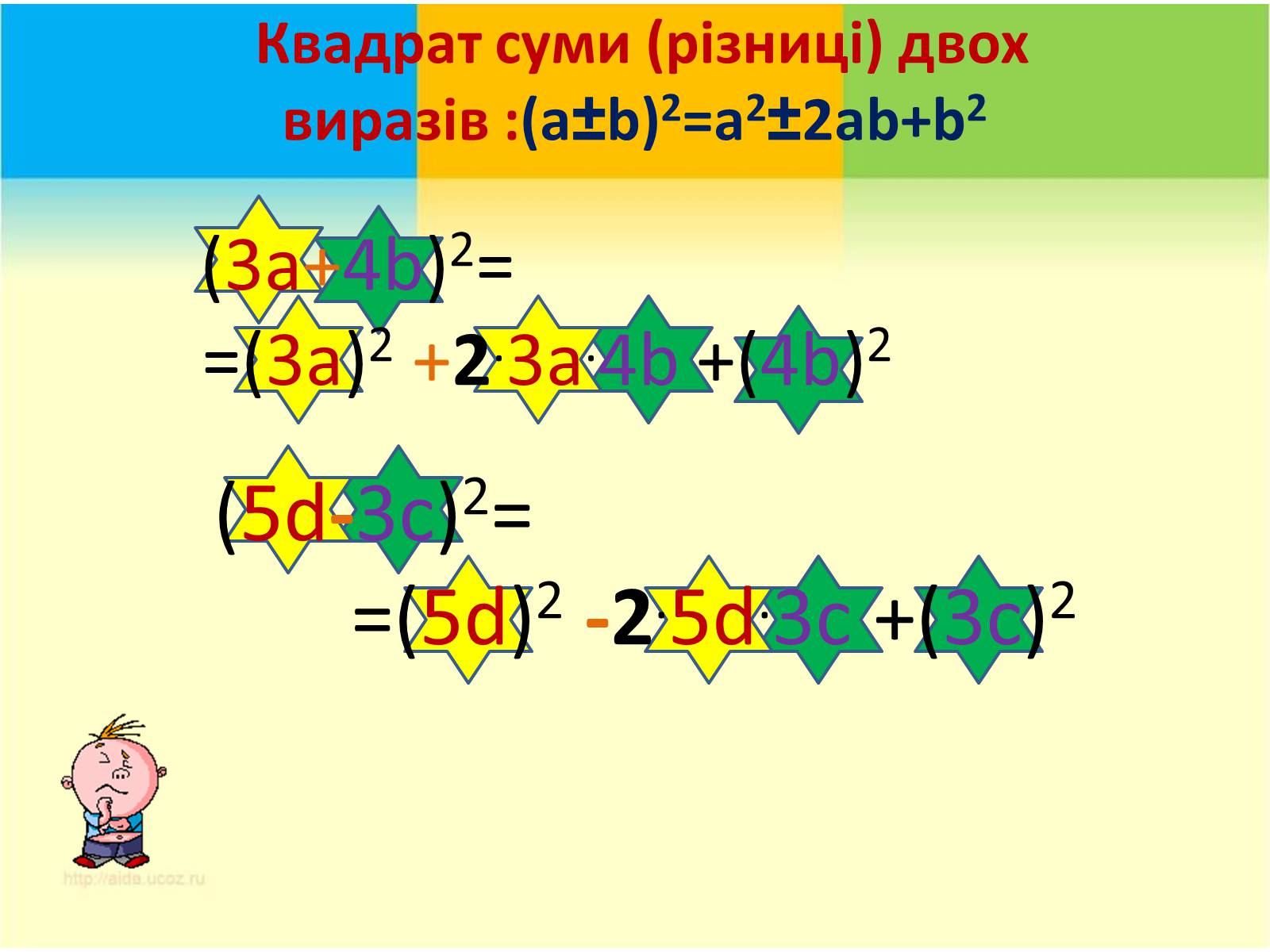
Квадрат суми (різниці) двох виразів :(a±b)2=a2±2ab+b2
(3a+4b)2=
=(3a)2 +2.3a.4b +(4b)2
(5d-3c)2=
=(5d)2 -2.5d.3c +(3c)2
(3a+4b)2=
=(3a)2 +2.3a.4b +(4b)2
(5d-3c)2=
=(5d)2 -2.5d.3c +(3c)2
Слайд #8
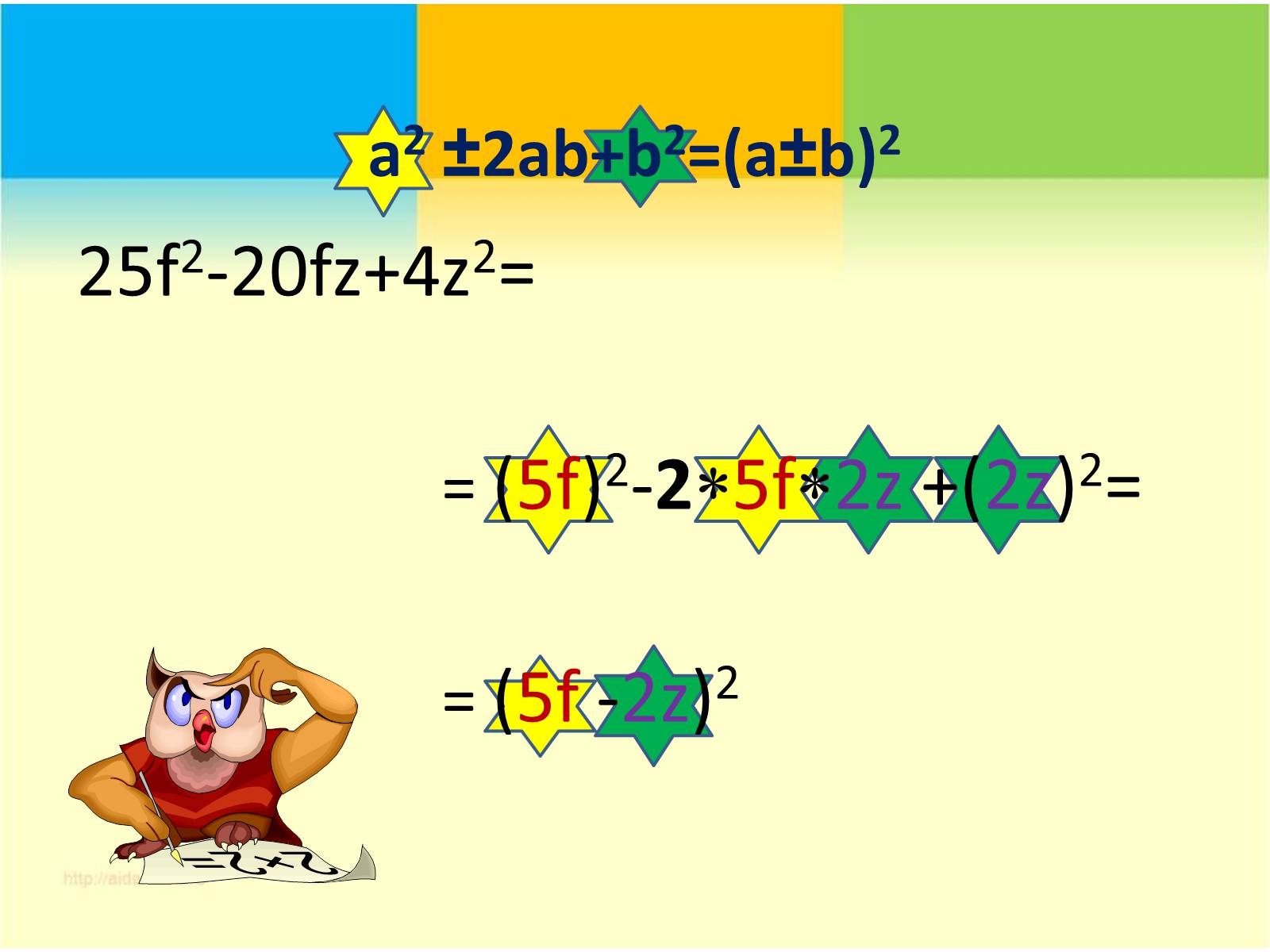
a2 ±2ab+b2=(a±b)2
25f2-20fz+4z2=
= (5f)2-25f2z +(2z)2=
= (5f -2z)2
25f2-20fz+4z2=
= (5f)2-25f2z +(2z)2=
= (5f -2z)2
Слайд #9
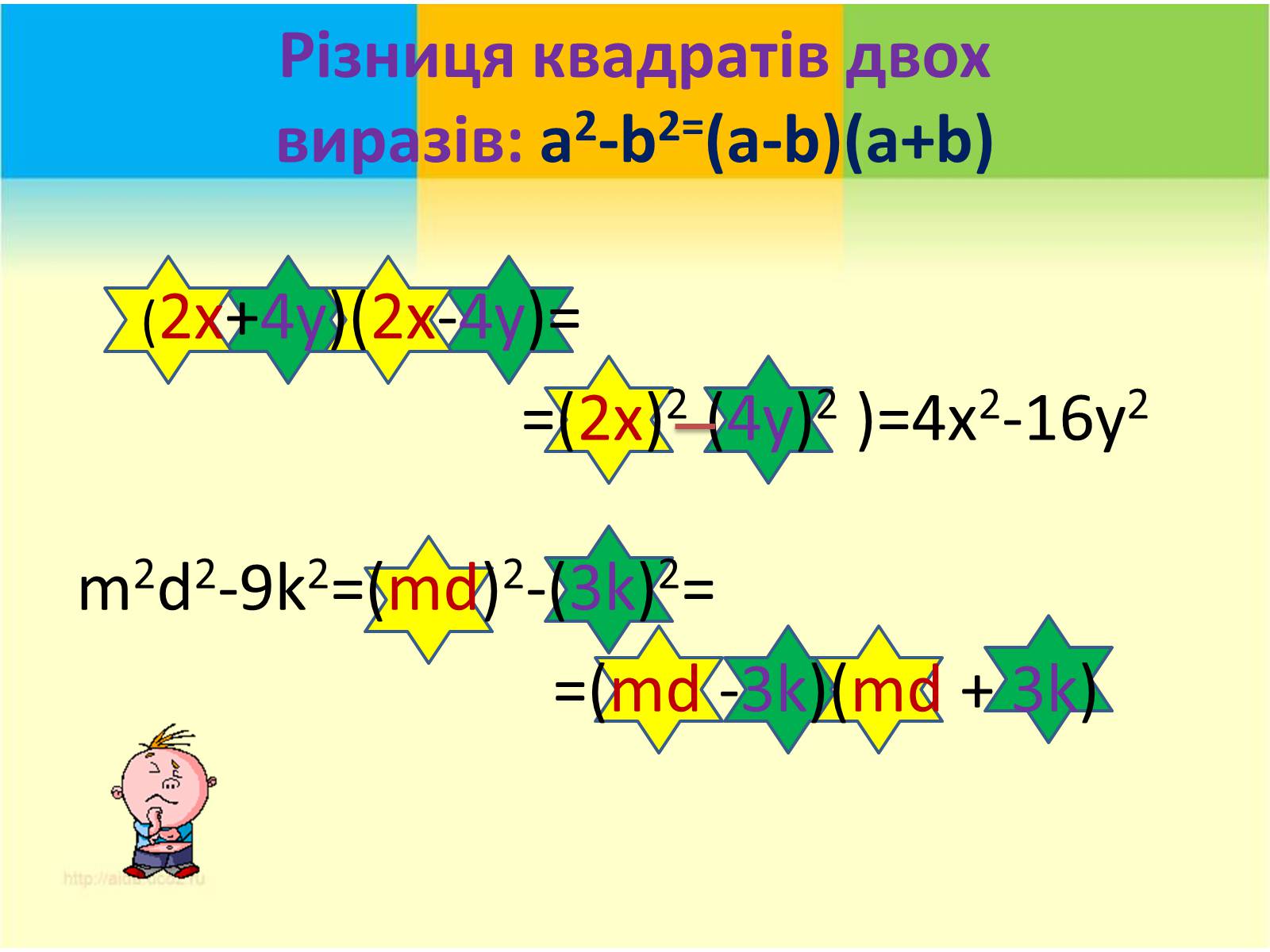
Різниця квадратів двох виразів: a2-b2=(a-b)(а+b)
(2x+4y)(2x-4y)=
=(2x)2 (4y)2 )=4x2-16y2
m2d2-9k2=(md)2-(3k)2=
=(md -3k)(md + 3k)
(2x+4y)(2x-4y)=
=(2x)2 (4y)2 )=4x2-16y2
m2d2-9k2=(md)2-(3k)2=
=(md -3k)(md + 3k)
Слайд #10
Знайдіть помилку :
1)(0,6a -0,1b)2 =
=(0,6a)2-20,6a0,1b+(0,1b)2 =
= 0,36a2-1,2аb+0,01b2
2) (7x+3y)(7x-3y) =(3у)2-(7х)2 )=9x2-49y2
0,12
1)(0,6a -0,1b)2 =
=(0,6a)2-20,6a0,1b+(0,1b)2 =
= 0,36a2-1,2аb+0,01b2
2) (7x+3y)(7x-3y) =(3у)2-(7х)2 )=9x2-49y2
0,12
Слайд #11
Заповніть пропуски в формулах:
(а +…)2 = … + 2аb + … ;
(а +b)2 = a 2 + 2аb + b2 ;
(а … b)… = а2 – 2аb + … ;
(а - b) 2 = а2 – 2аb + b2 ;
а3 - … = (а – b)(… + аb + …);
а3 - b3 = (а – b)(а2 + аb + b2);
а3 + b3 = (… …)(а2 … + b2);
а3 + b3 = (а + b)(а2 -ab + b2);
а2 – b2 = (… b)(а – …).
а2 – b2 = (a + b)(а – b).
(а +…)2 = … + 2аb + … ;
(а +b)2 = a 2 + 2аb + b2 ;
(а … b)… = а2 – 2аb + … ;
(а - b) 2 = а2 – 2аb + b2 ;
а3 - … = (а – b)(… + аb + …);
а3 - b3 = (а – b)(а2 + аb + b2);
а3 + b3 = (… …)(а2 … + b2);
а3 + b3 = (а + b)(а2 -ab + b2);
а2 – b2 = (… b)(а – …).
а2 – b2 = (a + b)(а – b).
Слайд #12
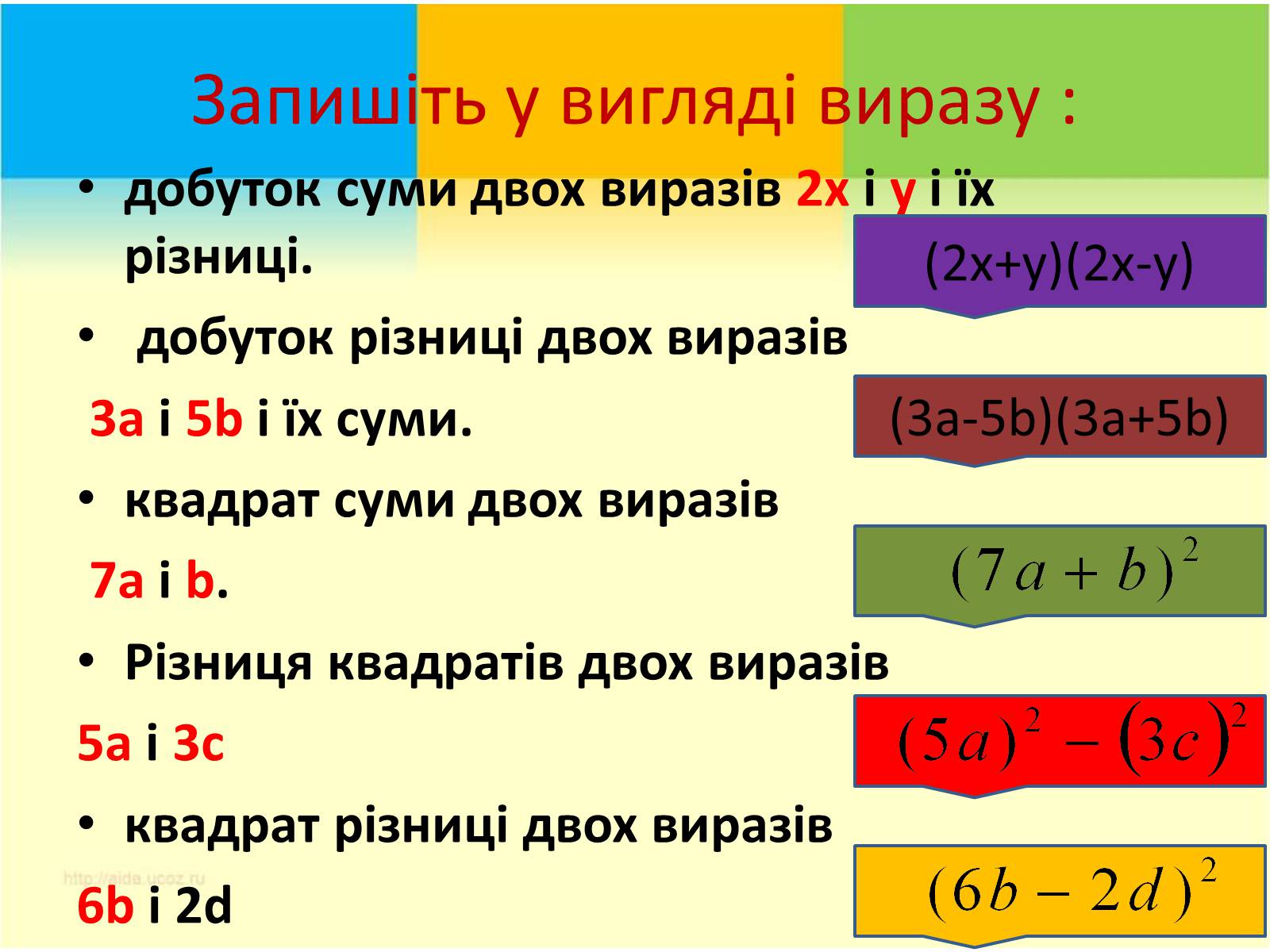
Запишіть у вигляді виразу :
добуток суми двох виразів 2х і y і їх різниці.
добуток різниці двох виразів
3a і 5b і їх суми.
квадрат суми двох виразів
7a і b.
Різниця квадратів двох виразів
5а і 3с
квадрат різниці двох виразів
6b і 2d
(2х+у)(2х-у)
(3а-5b)(3a+5b)
добуток суми двох виразів 2х і y і їх різниці.
добуток різниці двох виразів
3a і 5b і їх суми.
квадрат суми двох виразів
7a і b.
Різниця квадратів двох виразів
5а і 3с
квадрат різниці двох виразів
6b і 2d
(2х+у)(2х-у)
(3а-5b)(3a+5b)
Слайд #13
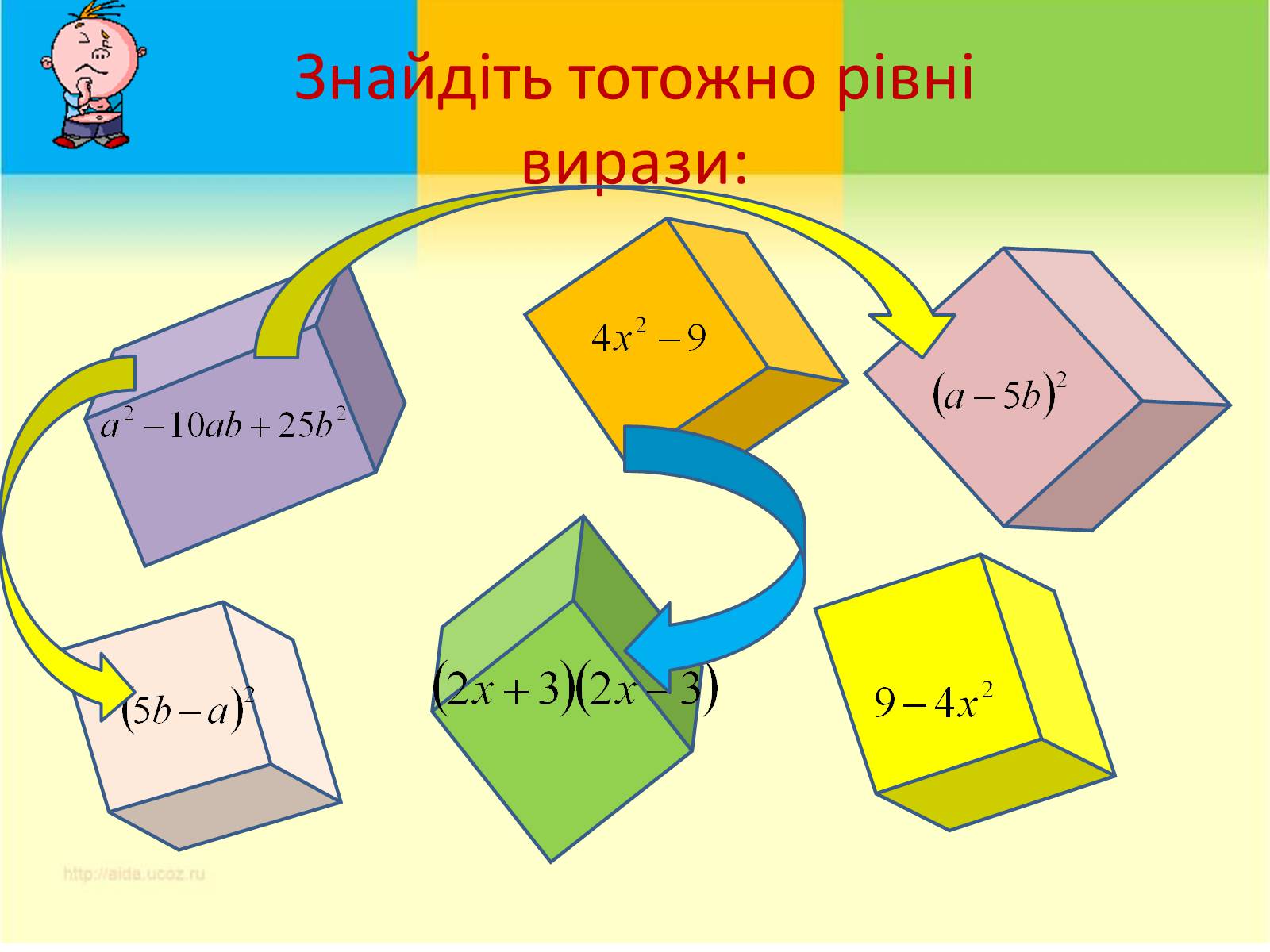
Знайдіть тотожно рівні вирази:
Слайд #14
Застосуйте відповідну формулу :
(3x+4y)2= (3x)2+23x4y+(4y)2 =9x2+24xy+16y2
(2d-7k)2=(2d)2-22d7k+(7k)2=4d2-28dk+49k2
(8d-k)(8d+k)= (8d)2-k2= 64d2-k2
(0,2a+0,5b)(0,5b-0,2a)=(0,5b)2-(0,2a)2 = =0,25b2-0,04a2
9-144y2 = 32-(12у)2 = (3-12у)(3+12у)
25m4-4k2 = (5m2)2-(2k)2= (5m2+2k)(5m2-2k)
(3x+4y)2= (3x)2+23x4y+(4y)2 =9x2+24xy+16y2
(2d-7k)2=(2d)2-22d7k+(7k)2=4d2-28dk+49k2
(8d-k)(8d+k)= (8d)2-k2= 64d2-k2
(0,2a+0,5b)(0,5b-0,2a)=(0,5b)2-(0,2a)2 = =0,25b2-0,04a2
9-144y2 = 32-(12у)2 = (3-12у)(3+12у)
25m4-4k2 = (5m2)2-(2k)2= (5m2+2k)(5m2-2k)
Слайд #15
МОЛОДЦІ!
