- Головна
- Готові шкільні презентації
- Презентація на тему «Квадратні корені» (варіант 2)
Презентація на тему «Квадратні корені» (варіант 2)
378
Слайд #1
Квадратні корені

Слайд #2
Багато чого з математики незалишається в пам'яті, але коли зрозумієш її, тоді при нагоді легко згадати призабуте. М.В.Остроградський

Слайд #3
Розв'язувати найпростіші рівняння з коренями
Знаходити ОДЗ найпростішого виразу, що
містить арифметичний квадратний корінь
Формувати первинні вміння добувати
арифметичний квадратний корінь із числа
Сформувати уявлення про спосіб розв'язання
найпростіших рівнянь виду
Засвоїти зміст понять «квадратний корінь
з числа», «означення арифметичного
квадратного кореня з невід'ємного числа»
Мета уроку:
Знаходити ОДЗ найпростішого виразу, що
містить арифметичний квадратний корінь
Формувати первинні вміння добувати
арифметичний квадратний корінь із числа
Сформувати уявлення про спосіб розв'язання
найпростіших рівнянь виду
Засвоїти зміст понять «квадратний корінь
з числа», «означення арифметичного
квадратного кореня з невід'ємного числа»
Мета уроку:

Слайд #4
Математичний диктант :
Варіант «Б»
1) Скільки точок перетину мають графіки функцій
у= -3х та у = x2 :
Варіант «А»
1) Яка з точок належить
графіку функції у = x2
1)1; 2) 2; 3) не перетинаються
4) безліч
2)
Яка з прямих перетинає графік функції у = x2
у= -1 3) у=1000
2) у= - 8 4) у= - 4-х
1) А (0,01; 0,1) 2) С (-10; 100)
3) Р( -0,5; -0,25)
2) Знайдіть значення аргументу, якщо значення функції у= x2 дорівнює 9 :
3; 2)-3 і 3 ; 3) 81.
Варіант «Б»
1) Скільки точок перетину мають графіки функцій
у= -3х та у = x2 :
Варіант «А»
1) Яка з точок належить
графіку функції у = x2
1)1; 2) 2; 3) не перетинаються
4) безліч
2)
Яка з прямих перетинає графік функції у = x2
у= -1 3) у=1000
2) у= - 8 4) у= - 4-х
1) А (0,01; 0,1) 2) С (-10; 100)
3) Р( -0,5; -0,25)
2) Знайдіть значення аргументу, якщо значення функції у= x2 дорівнює 9 :
3; 2)-3 і 3 ; 3) 81.

Слайд #5
Математичний диктант :
5) Складіть і розв'яжіть графічно рівняння, яке б мало один розв'язок у І чверті та один у ІІ чверті.
6) Побудуйте графік функції у = x2 для
-3 ≤ х ≤ 2.
3) Користуючись графіком
функції у = x2 , зображеним
на мал.38 (с.131) підручника,
знайдіть :
а) значення функції, якщо
значення аргументу дорівнює:
-1,2 ; 0,9; 1,4; 0.
б) значення аргументу, при якому значення функції дорівнює : 2; 4; 6; 9.
5) Складіть і розв'яжіть графічно рівняння, яке б мало один розв'язок у І чверті та один у ІІ чверті.
6) Побудуйте графік функції у = x2 для
-3 ≤ х ≤ 2.
3) Користуючись графіком
функції у = x2 , зображеним
на мал.38 (с.131) підручника,
знайдіть :
а) значення функції, якщо
значення аргументу дорівнює:
-1,2 ; 0,9; 1,4; 0.
б) значення аргументу, при якому значення функції дорівнює : 2; 4; 6; 9.

Слайд #6
Питання на повторення :
Інтерактивна вправа “Мікрофон”
Подайте у вигляді квадрата: 16; 81; ;
Знайти значення виразу : ; ;-
Порівняйте їх.
Назвати число, квадрат якого дорівнює 25 ; 36 ;
9 ; 121 ; 0 ; -9 .
Які числа задовольняють рівняння :
;
Інтерактивна вправа “Мікрофон”
Подайте у вигляді квадрата: 16; 81; ;
Знайти значення виразу : ; ;-
Порівняйте їх.
Назвати число, квадрат якого дорівнює 25 ; 36 ;
9 ; 121 ; 0 ; -9 .
Які числа задовольняють рівняння :
;

Слайд #7
Історична довідка :
З давних давен поряд із відшуканням площі квадрата за
відомою довжиною його сторони доводилося розв'язувати
обернену задачу: “ Якою повинна бути сторона квадрата,
щоб його площа дорівнювала а ?”
Таку задачу вміли розв'язувати ще 4 тисячі років тому
вавилонські вчені. Вони склали таблицю квадратів багатьох
натуральних чисел і, користуючись нею, знаходили
квадратні корені з чисел, які були в таблиці.
З давних давен поряд із відшуканням площі квадрата за
відомою довжиною його сторони доводилося розв'язувати
обернену задачу: “ Якою повинна бути сторона квадрата,
щоб його площа дорівнювала а ?”
Таку задачу вміли розв'язувати ще 4 тисячі років тому
вавилонські вчені. Вони склали таблицю квадратів багатьох
натуральних чисел і, користуючись нею, знаходили
квадратні корені з чисел, які були в таблиці.

Слайд #8
Квадратні корені
Квадратним коренем з числа а називають число, квадрат якого дорівнює а.
Наприклад :
Квадратними коренями числа 49 є 7 і -7 тому, що
= 49 і = 49.
Квадратний корінь з від'ємного числа не існує!
Квадратним коренем з числа а називають число, квадрат якого дорівнює а.
Наприклад :
Квадратними коренями числа 49 є 7 і -7 тому, що
= 49 і = 49.
Квадратний корінь з від'ємного числа не існує!

Слайд #9
Арифметичний квадратний корінь
Арифметичним квадратним коренем з числа а
називають невід'ємне число, квадрат якого
дорівнює а. ≥ 0 і = а
- знак арифметичного квадратного кореня
або радикал (від латинського слова radix - корінь)
а - підкореневий вираз
Арифметичним квадратним коренем з числа а
називають невід'ємне число, квадрат якого
дорівнює а. ≥ 0 і = а
- знак арифметичного квадратного кореня
або радикал (від латинського слова radix - корінь)
а - підкореневий вираз

Слайд #10
Історична довідка :
У ХІІІ-ХУ ст. європейські математики,
скорочуючи слово radix, позначали
квадратний корінь знаками R, . Наприклад,
запис мав такий вигляд : 7. У ХУІ ст.
стали використовувати знак √. Походження
цього символу, мабуть, пов'язано з
рукописною буквою r..
Рене Декарт
(1596 - 1650)
У ХУІІ ст. видатний французький математик Рене Декарт, поєднавши знак √ з горизонтальною рискою, отримав символ .
У ХІІІ-ХУ ст. європейські математики,
скорочуючи слово radix, позначали
квадратний корінь знаками R, . Наприклад,
запис мав такий вигляд : 7. У ХУІ ст.
стали використовувати знак √. Походження
цього символу, мабуть, пов'язано з
рукописною буквою r..
Рене Декарт
(1596 - 1650)
У ХУІІ ст. видатний французький математик Рене Декарт, поєднавши знак √ з горизонтальною рискою, отримав символ .

Слайд #11
Запам'ятай !
Якщо в ≥ 0 і = а , то .
Для будь – якого невід'ємного числа а справедливо, що ≥ 0 і = а .
Якщо в ≥ 0 і = а , то .
Для будь – якого невід'ємного числа а справедливо, що ≥ 0 і = а .

Слайд #12
Завдання :
1. Покажіть, що 13 – арифметичне значення квадратного кореня із 169.
Розв'язання : = 169, 13 – число додатне, тому
2.Знайдіть значення виразу .
Розв'язання :
, бо 15 > 0 і =225.
1. Покажіть, що 13 – арифметичне значення квадратного кореня із 169.
Розв'язання : = 169, 13 – число додатне, тому
2.Знайдіть значення виразу .
Розв'язання :
, бо 15 > 0 і =225.

Слайд #13
Завдання :
3. Розв'яжіть рівняння : .
а) б)
Розв'язання :
а) , 5 > 0, = х + 3 ; х = 22.
Відповідь : 22.
б) , ,
; ;
Відповідь : 1.
13
3. Розв'яжіть рівняння : .
а) б)
Розв'язання :
а) , 5 > 0, = х + 3 ; х = 22.
Відповідь : 22.
б) , ,
; ;
Відповідь : 1.
13

Слайд #14
Підсумок уроку: “доповніть речення “
Квадратний корінь з числа а – це …
З додатного числа а існує … різних квадратних корені.
З числа 0 існує … квадратних корені.
Арифметичне значення квадратного кореня з числа а – це …
З Рівняння = 100 має корені …
Квадратний корінь з числа а – це …
З додатного числа а існує … різних квадратних корені.
З числа 0 існує … квадратних корені.
Арифметичне значення квадратного кореня з числа а – це …
З Рівняння = 100 має корені …

Слайд #15
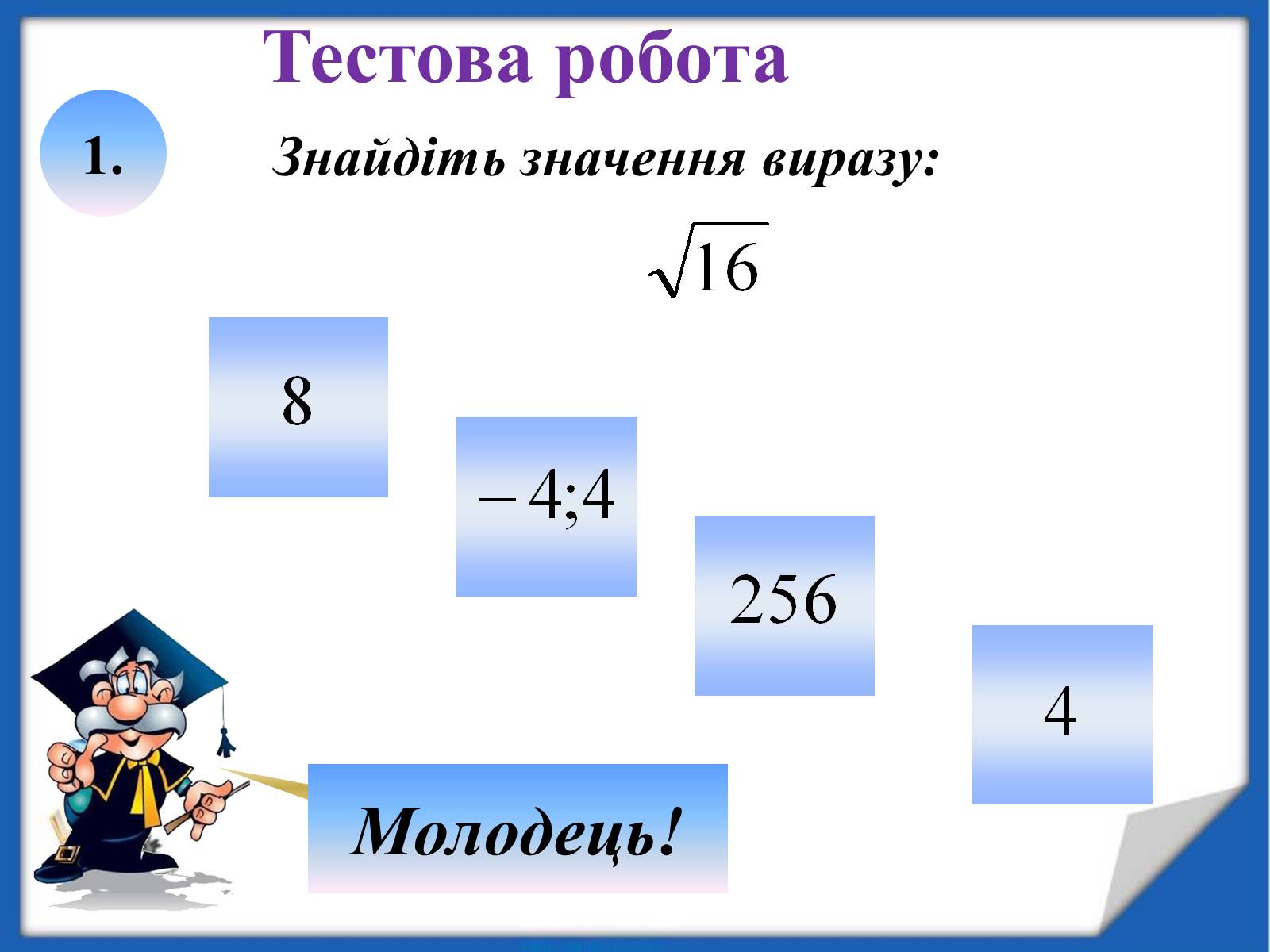
1.
Знайдіть значення виразу:
Невірно!
Молодець!
Тестова робота
Знайдіть значення виразу:
Невірно!
Молодець!
Тестова робота
Слайд #16
2.
Невірно!
Молодець!
Знайдіть значення виразу:
Невірно!
Молодець!
Знайдіть значення виразу:

Слайд #17
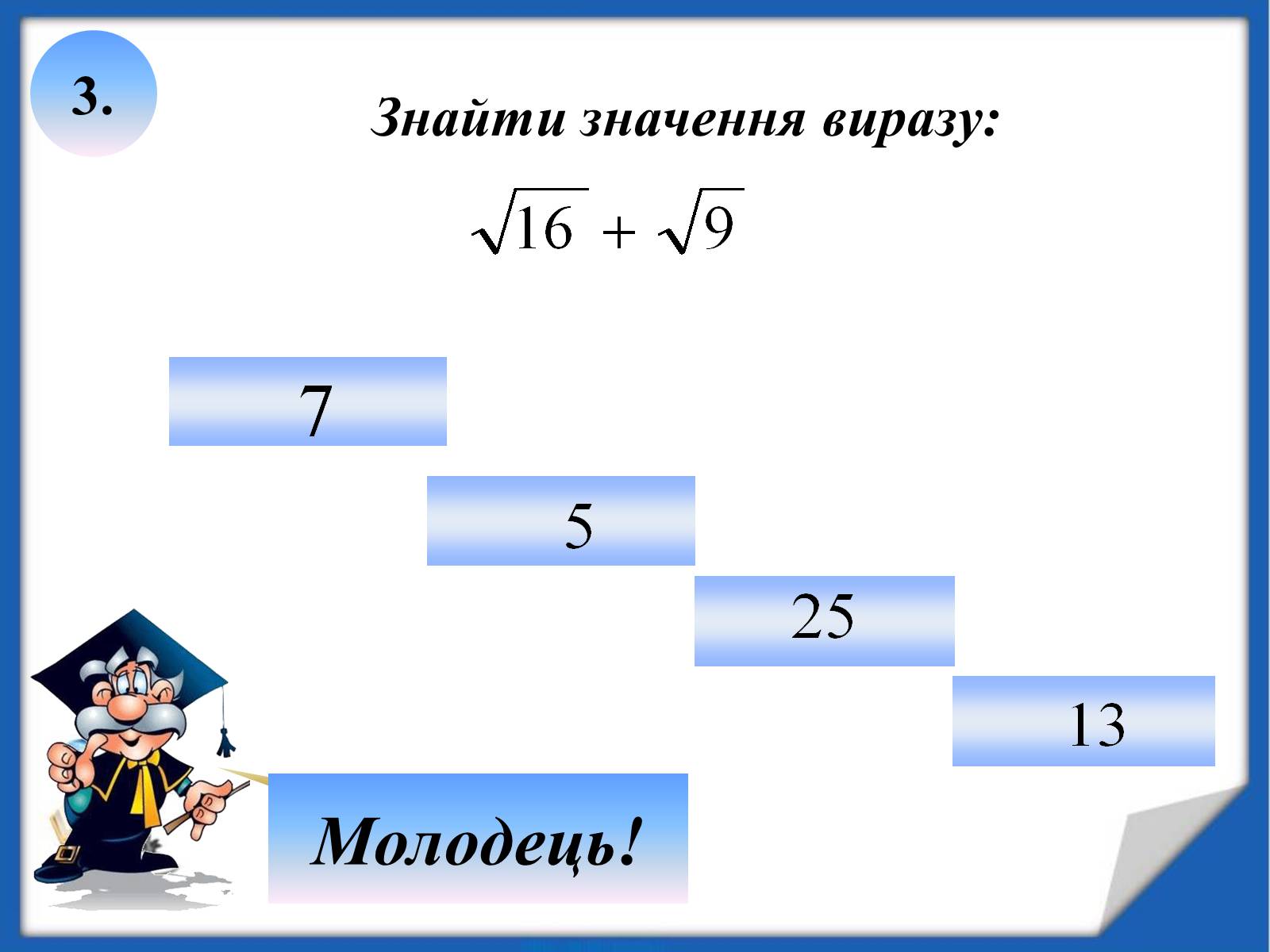
3.
Знайти значення виразу:
Невірно!
Молодець!
Знайти значення виразу:
Невірно!
Молодець!
Слайд #18
4.
Невірно!
Молодець!
Знайти значення виразу :
Невірно!
Молодець!
Знайти значення виразу :

Слайд #19
5.
Невірно!
Молодець!
Яка із рівностей правильна :
Невірно!
Молодець!
Яка із рівностей правильна :

Слайд #20
6.
Невірно!
Молодець!
Яка рівність є хибною :
Невірно!
Молодець!
Яка рівність є хибною :

Слайд #21
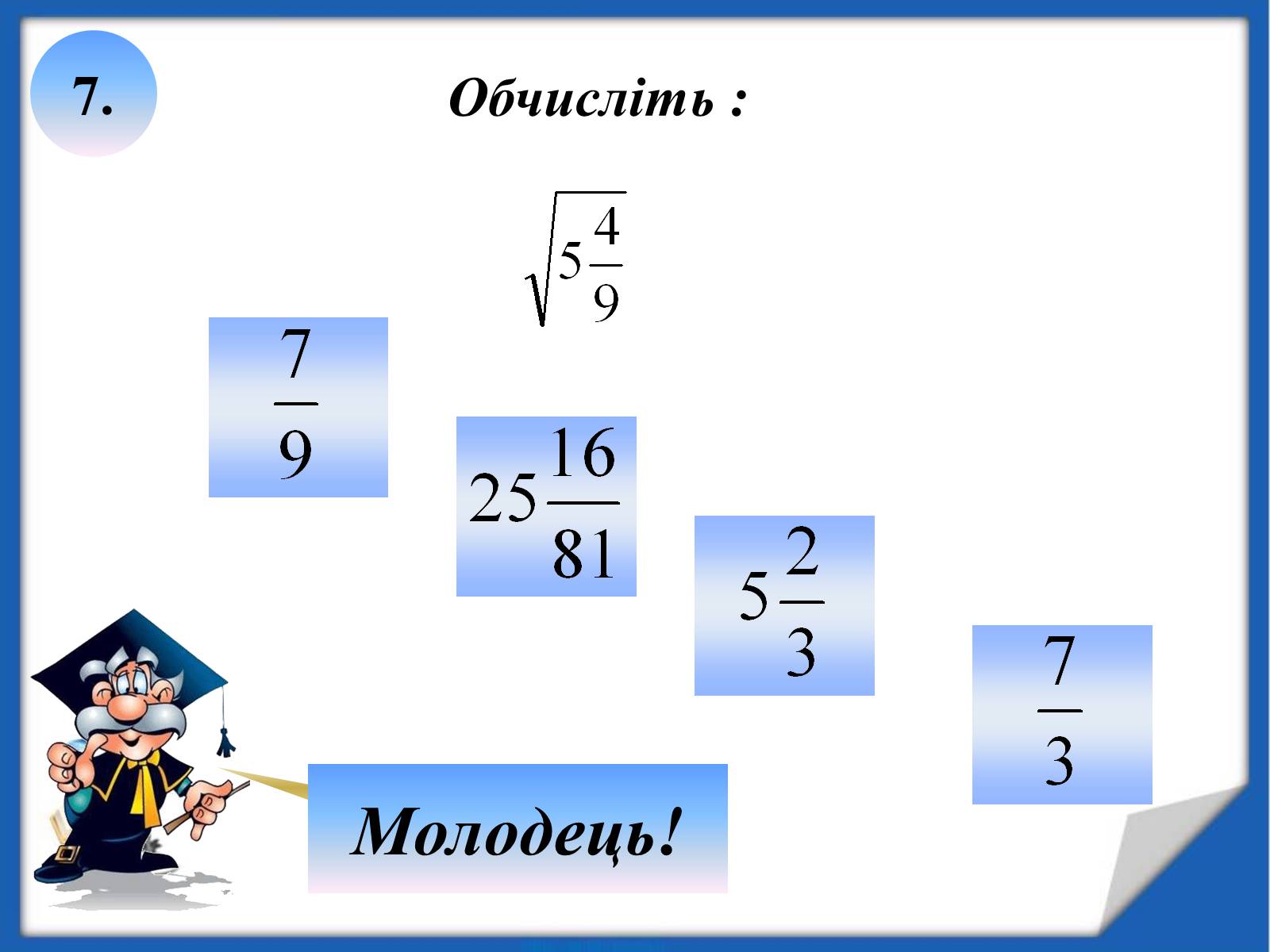
7.
Обчисліть :
Невірно!
Молодець!
Обчисліть :
Невірно!
Молодець!
Слайд #22
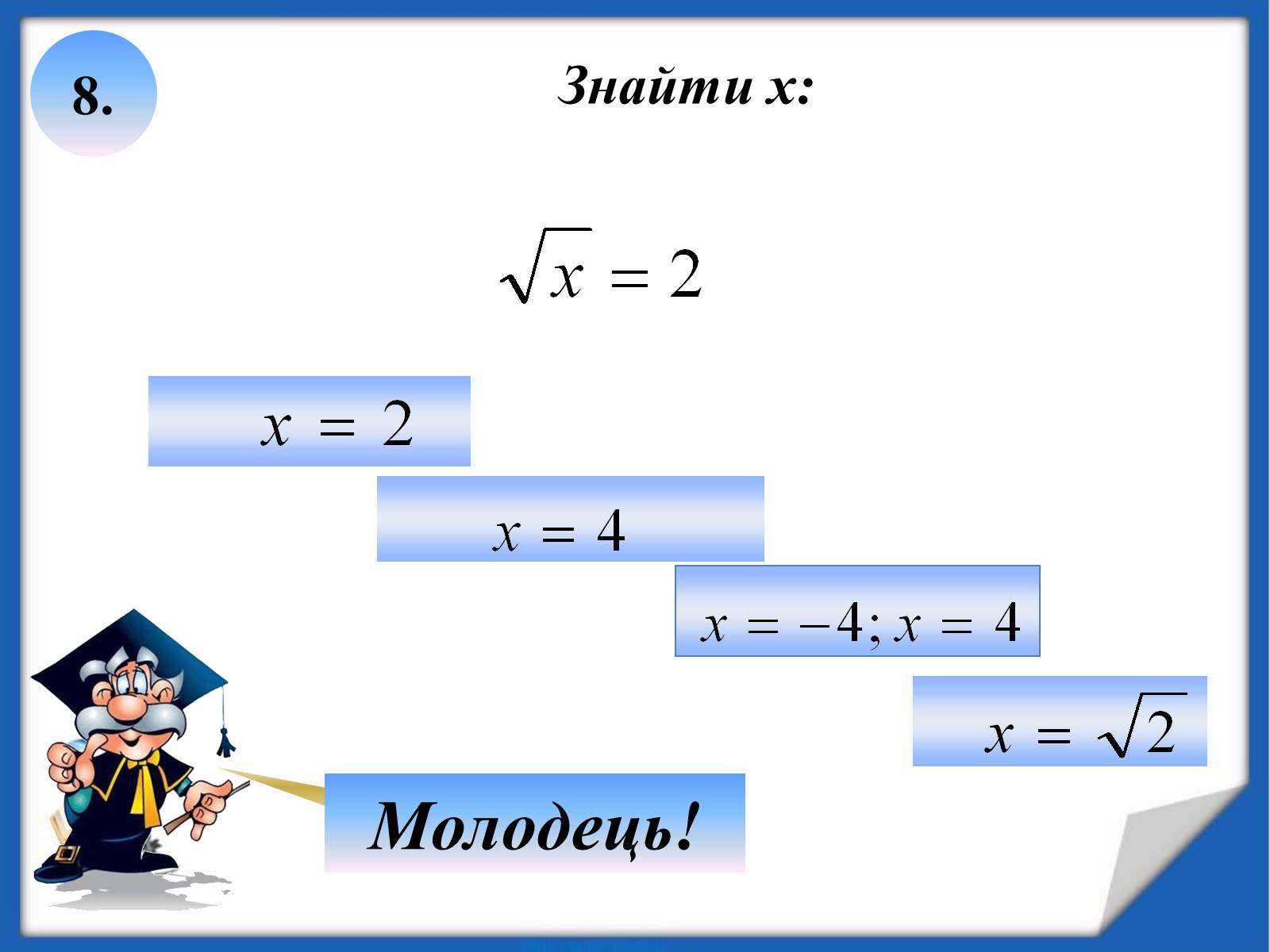
8.
Знайти х:
Невірно!
Молодець!
Знайти х:
Невірно!
Молодець!
Слайд #23
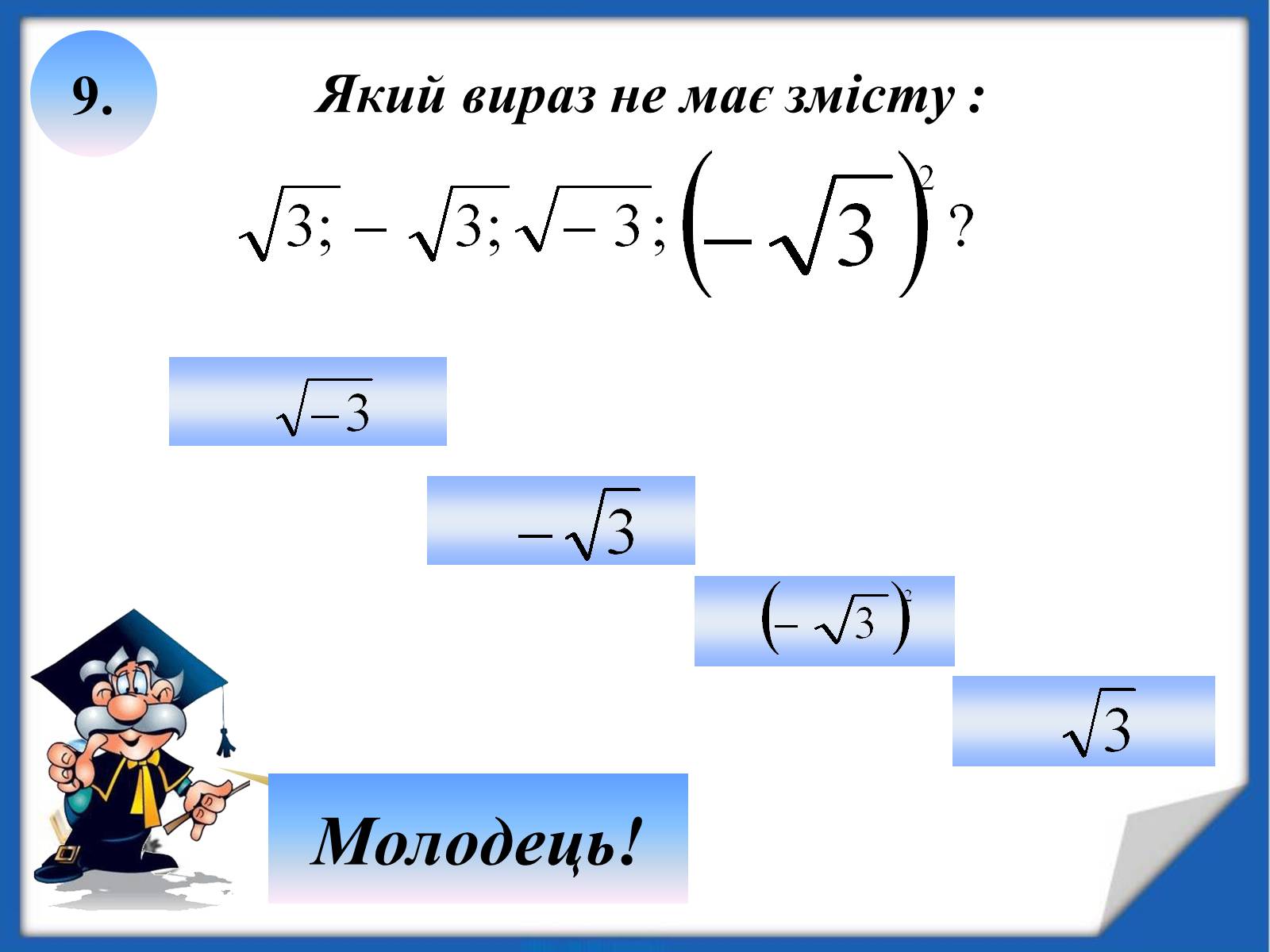
9.
Який вираз не має змісту :
Невірно!
Молодець!
Який вираз не має змісту :
Невірно!
Молодець!
Слайд #24
Домашнє завдання
Опрацювати п.14 (с.135) .
Рівень А: №№ 618, 621, 622,
626 (с.138) ;
Рівень Б : №№ 646, 649, 652, 654 (с.141).
Опрацювати п.14 (с.135) .
Рівень А: №№ 618, 621, 622,
626 (с.138) ;
Рівень Б : №№ 646, 649, 652, 654 (с.141).
