- Головна
- Готові шкільні презентації
- Презентація на тему «Системи рівнянь з параметрами»
Презентація на тему «Системи рівнянь з параметрами»
626
Слайд #1
Проектна робота з теми:“ Системи рівнянь з параметрами ”
Виконала учениця 11 х/б класу Педан Поліна
Керівник проекту: Вчитель математики вищої категорії Шкаран Ніна Іванівна
Виконала учениця 11 х/б класу Педан Поліна
Керівник проекту: Вчитель математики вищої категорії Шкаран Ніна Іванівна

Слайд #2
Мета проекту:
Сформувати вміння та навички розв'язувати системи двох рівнянь з двома змінними з параметрами; розвивати інтерес, творчі здібності та інтуїцію учнів, вміння застосовувати набуті знання в нових ситуаціях, виховувати зібраність, працьовитість, охайність, організованість, графічну та математичну культуру.
Завдання з параметрами вважаються важними для розуміння і засвоєння учнями.
Але Задачі з параметрами традиційно входять до завдань ДПА та ЗНО з математики.
Проектна робота пропонує системи рівнянь з параметрами, і має за мету допомогти учням 9 класу чітко і логічно застосовувати математичні твердження, знаходити неординарні методи їх розв'язування.
Сформувати вміння та навички розв'язувати системи двох рівнянь з двома змінними з параметрами; розвивати інтерес, творчі здібності та інтуїцію учнів, вміння застосовувати набуті знання в нових ситуаціях, виховувати зібраність, працьовитість, охайність, організованість, графічну та математичну культуру.
Завдання з параметрами вважаються важними для розуміння і засвоєння учнями.
Але Задачі з параметрами традиційно входять до завдань ДПА та ЗНО з математики.
Проектна робота пропонує системи рівнянь з параметрами, і має за мету допомогти учням 9 класу чітко і логічно застосовувати математичні твердження, знаходити неординарні методи їх розв'язування.

Слайд #3
.
.
.
у
1) х+у=6 - пряма
х ²+ у ² = а - коло
Відповідь:
1) якщо r кола <18, то розв'язків немає;
2) якщо r кола=18, то розв'язок 1;
3) якщо r кола>18, то розв'язків 2;
.
6
6
F
О
А
В
х
1
1
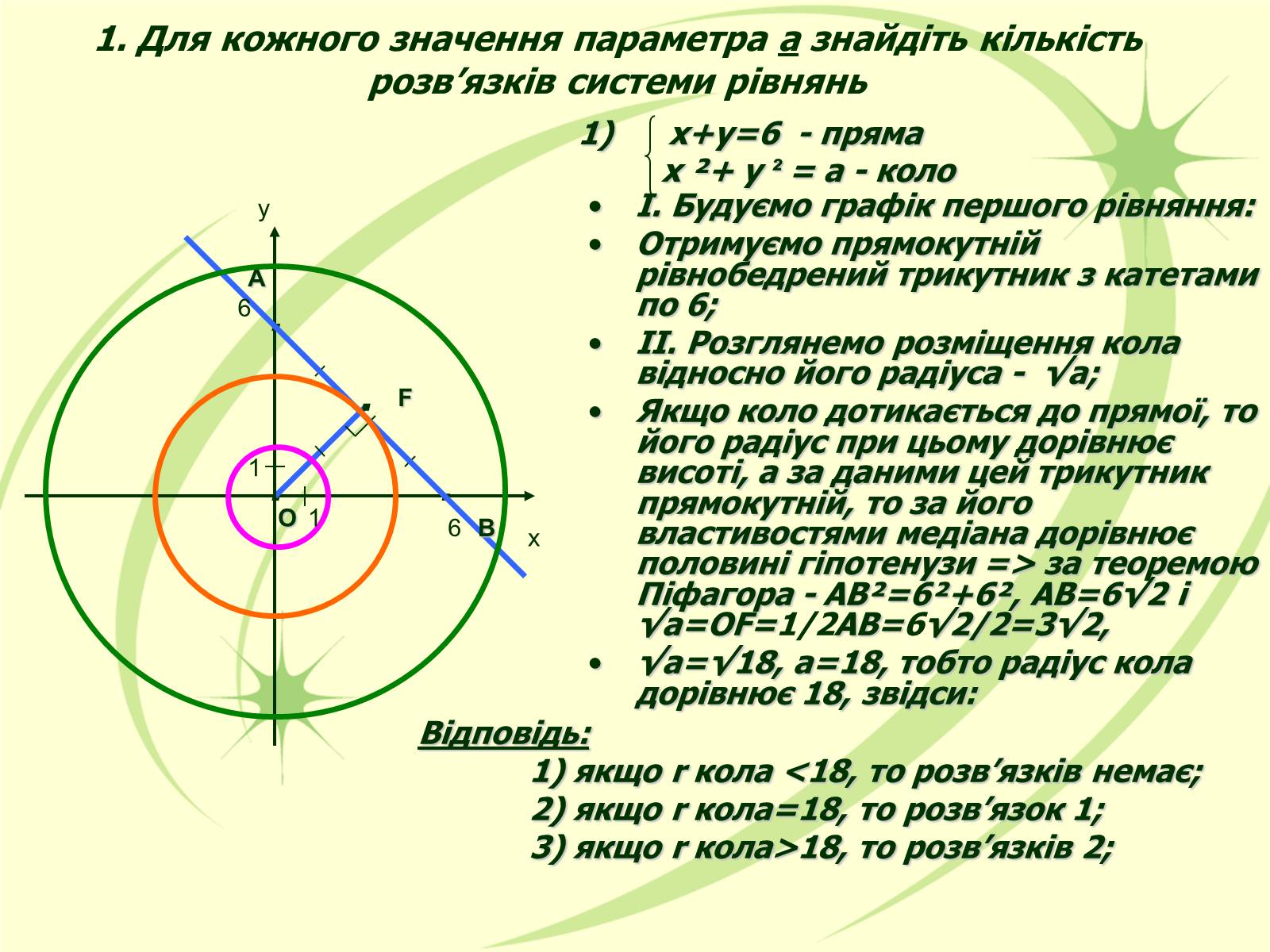
1. Для кожного значення параметра а знайдіть кількість розв'язків системи рівнянь
І. Будуємо графік першого рівняння:
Отримуємо прямокутній рівнобедрений трикутник з катетами по 6;
ІІ. Розглянемо розміщення кола відносно його радіуса - √а;
Якщо коло дотикається до прямої, то його радіус при цьому дорівнює висоті, а за даними цей трикутник прямокутній, то за його властивостями медіана дорівнює половині гіпотенузи => за теоремою Піфагора - АВ²=6²+6², АВ=6√2 і √а=OF=1/2АВ=6√2/2=3√2,
√а=√18, а=18, тобто радіус кола дорівнює 18, звідси:
.
.
у
1) х+у=6 - пряма
х ²+ у ² = а - коло
Відповідь:
1) якщо r кола <18, то розв'язків немає;
2) якщо r кола=18, то розв'язок 1;
3) якщо r кола>18, то розв'язків 2;
.
6
6
F
О
А
В
х
1
1
1. Для кожного значення параметра а знайдіть кількість розв'язків системи рівнянь
І. Будуємо графік першого рівняння:
Отримуємо прямокутній рівнобедрений трикутник з катетами по 6;
ІІ. Розглянемо розміщення кола відносно його радіуса - √а;
Якщо коло дотикається до прямої, то його радіус при цьому дорівнює висоті, а за даними цей трикутник прямокутній, то за його властивостями медіана дорівнює половині гіпотенузи => за теоремою Піфагора - АВ²=6²+6², АВ=6√2 і √а=OF=1/2АВ=6√2/2=3√2,
√а=√18, а=18, тобто радіус кола дорівнює 18, звідси:
Слайд #4
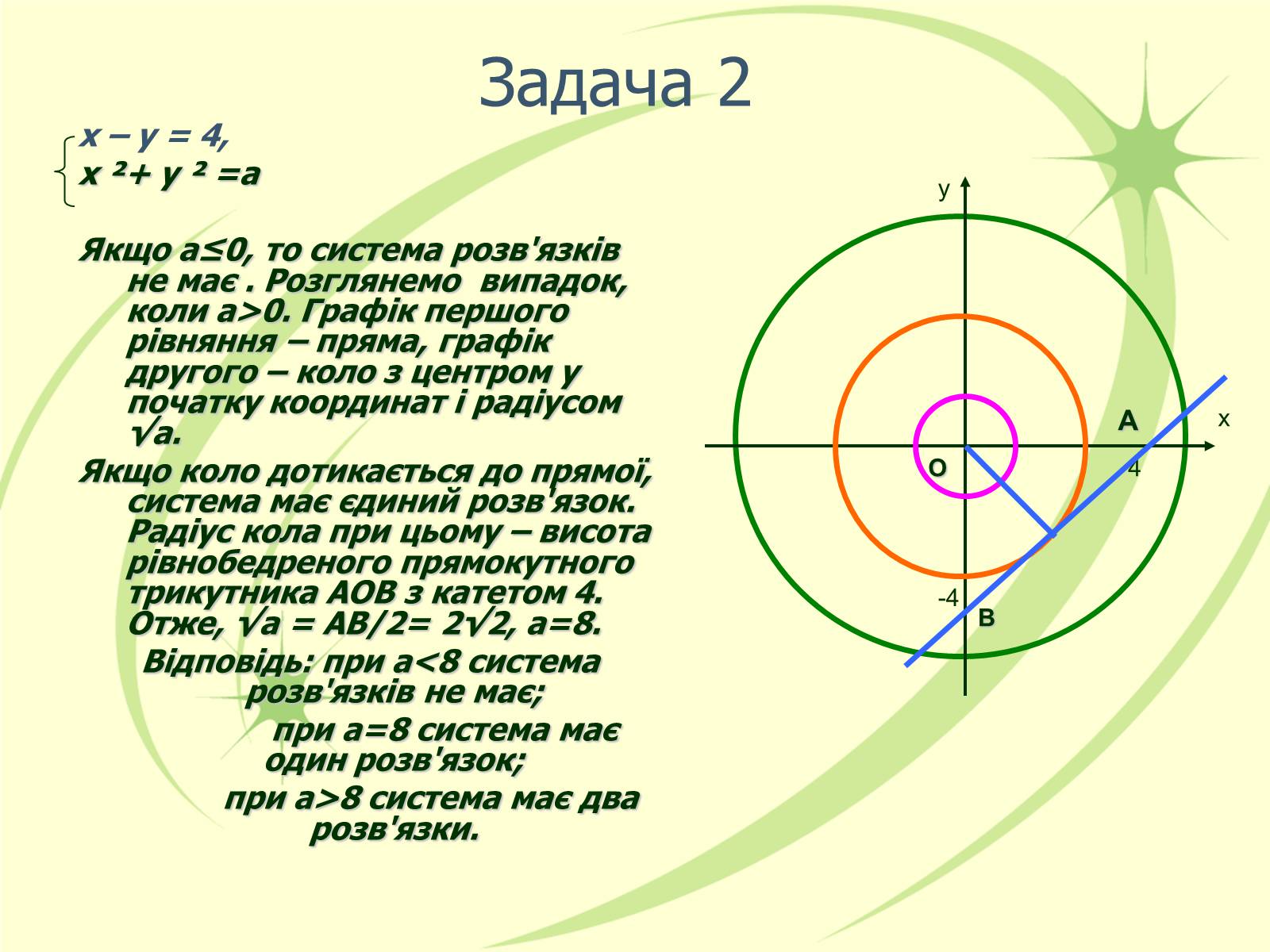
Задача 2
х – у = 4,
х ²+ у ² =а
Якщо а≤0, то система розв'язків не має . Розглянемо випадок, коли а>0. Графік першого рівняння – пряма, графік другого – коло з центром у початку координат і радіусом √а.
Якщо коло дотикається до прямої, система має єдиний розв'язок. Радіус кола при цьому – висота рівнобедреного прямокутного трикутника АОВ з катетом 4. Отже, √а = АВ/2= 2√2, а=8.
Відповідь: при а<8 система розв'язків не має;
при а=8 система має один розв'язок;
при а>8 система має два розв'язки.
А
4
-4
В
О
у
х
х – у = 4,
х ²+ у ² =а
Якщо а≤0, то система розв'язків не має . Розглянемо випадок, коли а>0. Графік першого рівняння – пряма, графік другого – коло з центром у початку координат і радіусом √а.
Якщо коло дотикається до прямої, система має єдиний розв'язок. Радіус кола при цьому – висота рівнобедреного прямокутного трикутника АОВ з катетом 4. Отже, √а = АВ/2= 2√2, а=8.
Відповідь: при а<8 система розв'язків не має;
при а=8 система має один розв'язок;
при а>8 система має два розв'язки.
А
4
-4
В
О
у
х
Слайд #5
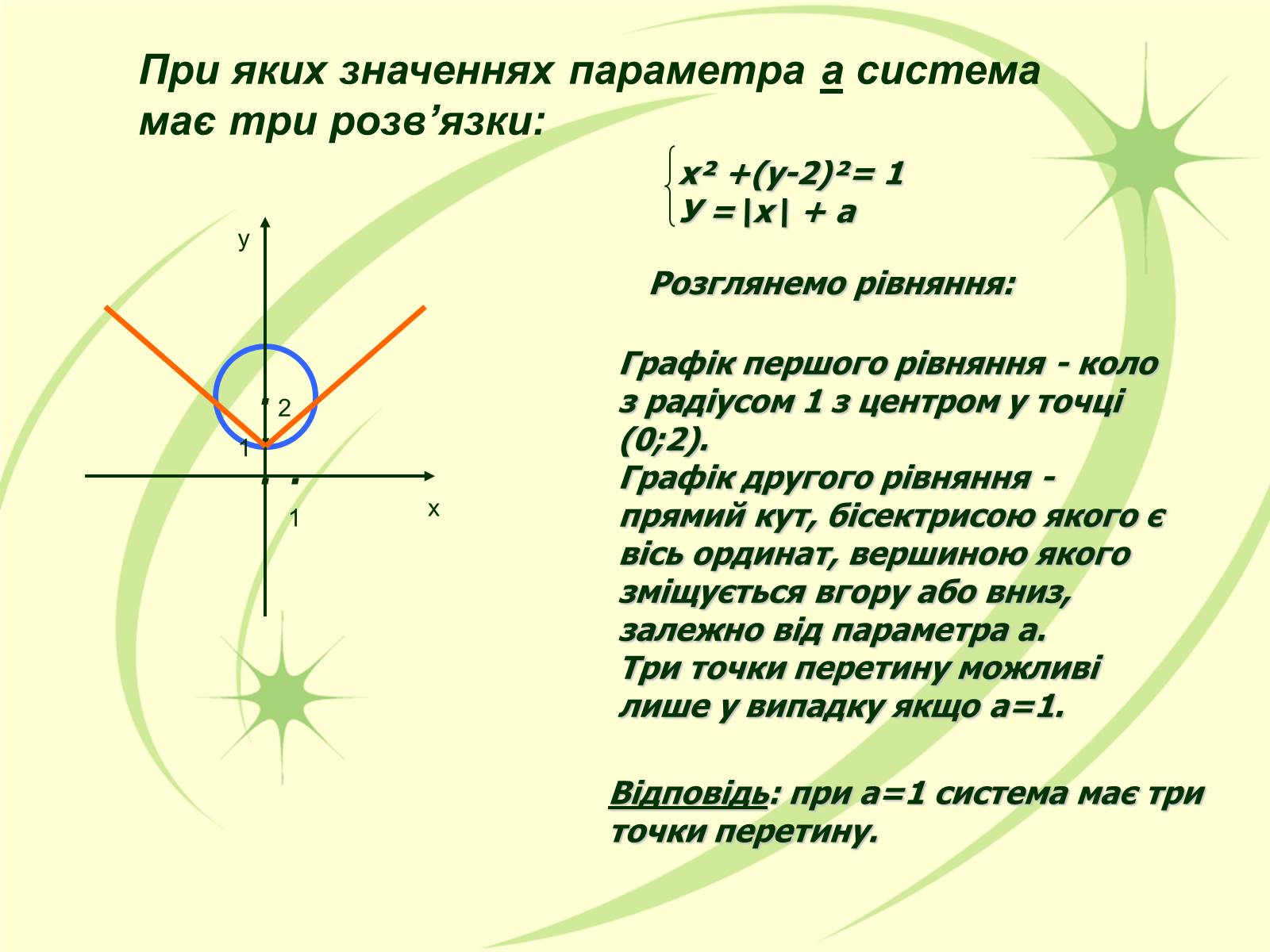
При яких значеннях параметра а система має три розв'язки:
х² +(у-2)²= 1
У =х + а
Розглянемо рівняння:
Графік першого рівняння - коло з радіусом 1 з центром у точці (0;2).
Графік другого рівняння - прямий кут, бісектрисою якого є вісь ординат, вершиною якого зміщується вгору або вниз, залежно від параметра а.
Три точки перетину можливі лише у випадку якщо а=1.
Відповідь: при а=1 система має три точки перетину.
.
.
.
2
.
1
1
у
х
х² +(у-2)²= 1
У =х + а
Розглянемо рівняння:
Графік першого рівняння - коло з радіусом 1 з центром у точці (0;2).
Графік другого рівняння - прямий кут, бісектрисою якого є вісь ординат, вершиною якого зміщується вгору або вниз, залежно від параметра а.
Три точки перетину можливі лише у випадку якщо а=1.
Відповідь: при а=1 система має три точки перетину.
.
.
.
2
.
1
1
у
х
Слайд #6
У = а + √х
2х+у-1=0
Розв'язання:
Графік другого рівняння буде пряма, першого - вітка параболи, що знаходиться в І четверті, і буде рухатись по осі ординат відносно параметра а.
Отже, побудуємо графіки цих рівнянь в одній системі координат.
Оскільки розміщення вітки параболи буде залежати від параметра а, то:
якщо а є(-∞; 1], то система має один корінь;
якщо а є(1; +∞),то система коренів не має.
Відповідь: 1) якщо а є(-∞; 1], то система має один корінь,
2) якщо а є(1; +∞),то система
коренів не має.
.
.
.
.
1
у
.
1
х
2
.
5
2
.
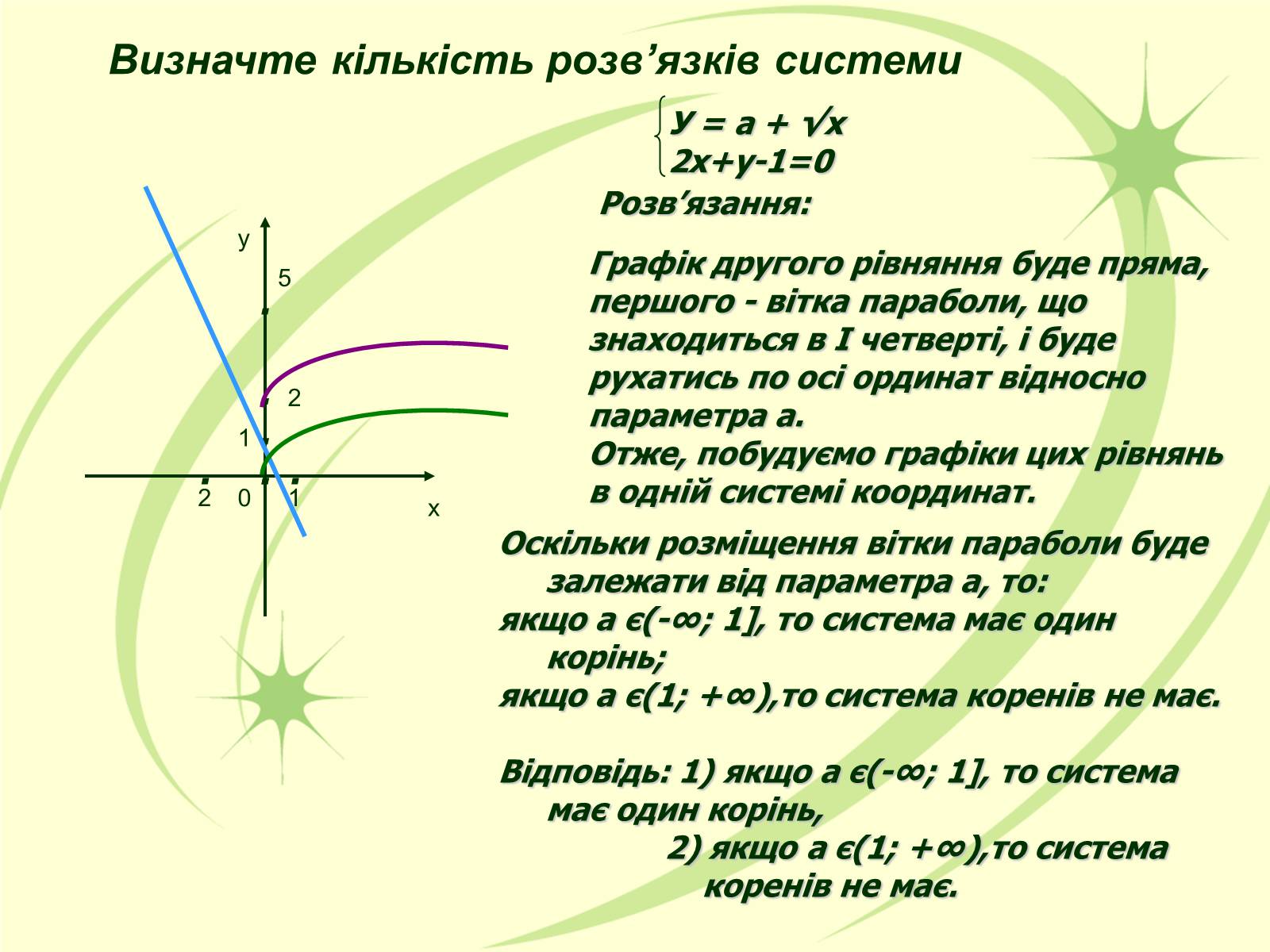
Визначте кількість розв'язків системи
2х+у-1=0
Розв'язання:
Графік другого рівняння буде пряма, першого - вітка параболи, що знаходиться в І четверті, і буде рухатись по осі ординат відносно параметра а.
Отже, побудуємо графіки цих рівнянь в одній системі координат.
Оскільки розміщення вітки параболи буде залежати від параметра а, то:
якщо а є(-∞; 1], то система має один корінь;
якщо а є(1; +∞),то система коренів не має.
Відповідь: 1) якщо а є(-∞; 1], то система має один корінь,
2) якщо а є(1; +∞),то система
коренів не має.
.
.
.
.
1
у
.
1
х
2
.
5
2
.
Визначте кількість розв'язків системи
Слайд #7
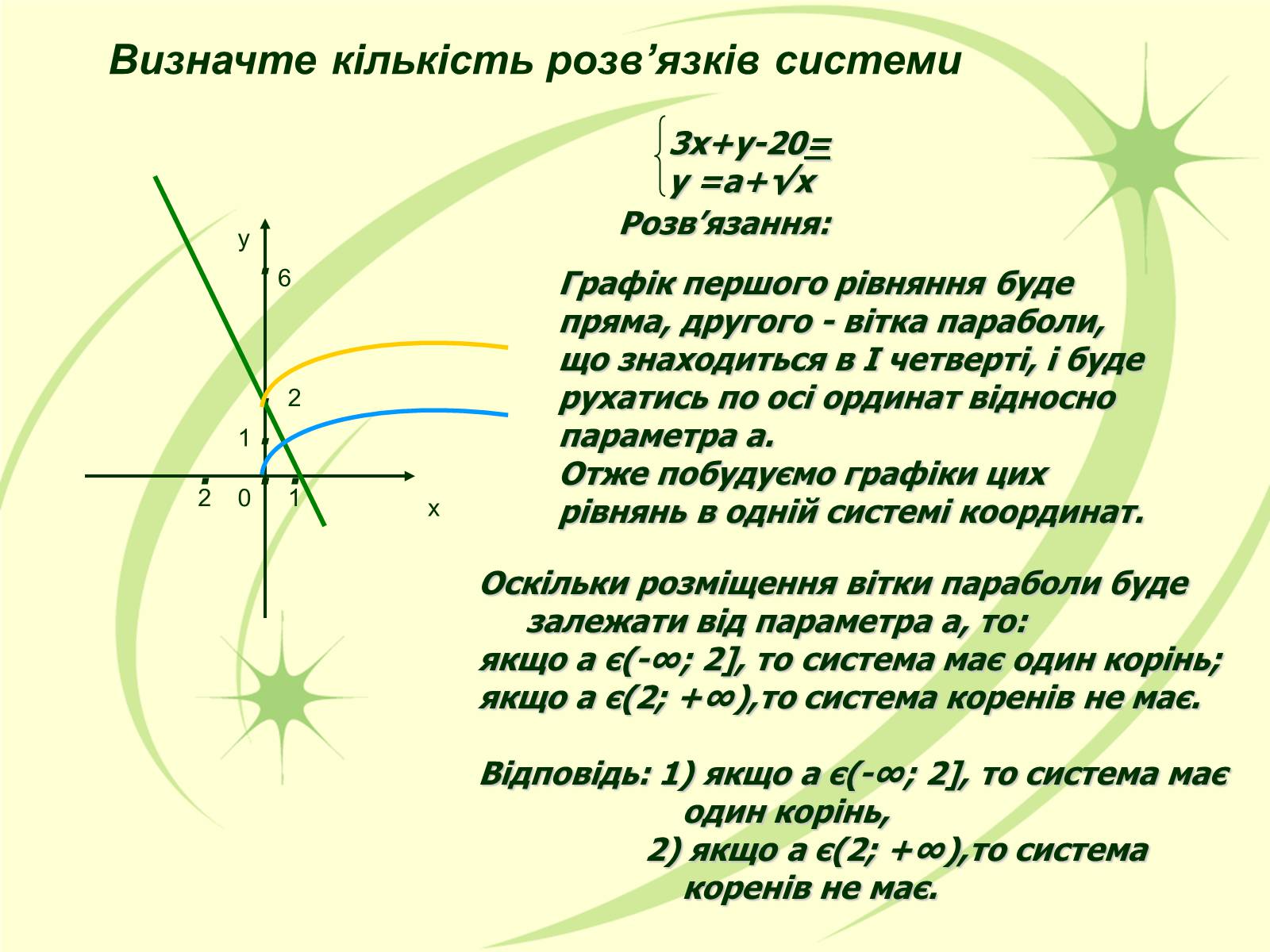
Визначте кількість розв'язків системи
3х+у-20=
у =а+√х
Розв'язання:
Графік першого рівняння буде пряма, другого - вітка параболи, що знаходиться в І четверті, і буде рухатись по осі ординат відносно параметра а.
Отже побудуємо графіки цих рівнянь в одній системі координат.
Оскільки розміщення вітки параболи буде залежати від параметра а, то:
якщо а є(-∞; 2], то система має один корінь;
якщо а є(2; +∞),то система коренів не має.
Відповідь: 1) якщо а є(-∞; 2], то система має
один корінь,
2) якщо а є(2; +∞),то система
коренів не має.
.
.
.
.
1
1
у
.
2
х
2
.
6
.
3х+у-20=
у =а+√х
Розв'язання:
Графік першого рівняння буде пряма, другого - вітка параболи, що знаходиться в І четверті, і буде рухатись по осі ординат відносно параметра а.
Отже побудуємо графіки цих рівнянь в одній системі координат.
Оскільки розміщення вітки параболи буде залежати від параметра а, то:
якщо а є(-∞; 2], то система має один корінь;
якщо а є(2; +∞),то система коренів не має.
Відповідь: 1) якщо а є(-∞; 2], то система має
один корінь,
2) якщо а є(2; +∞),то система
коренів не має.
.
.
.
.
1
1
у
.
2
х
2
.
6
.
Слайд #8
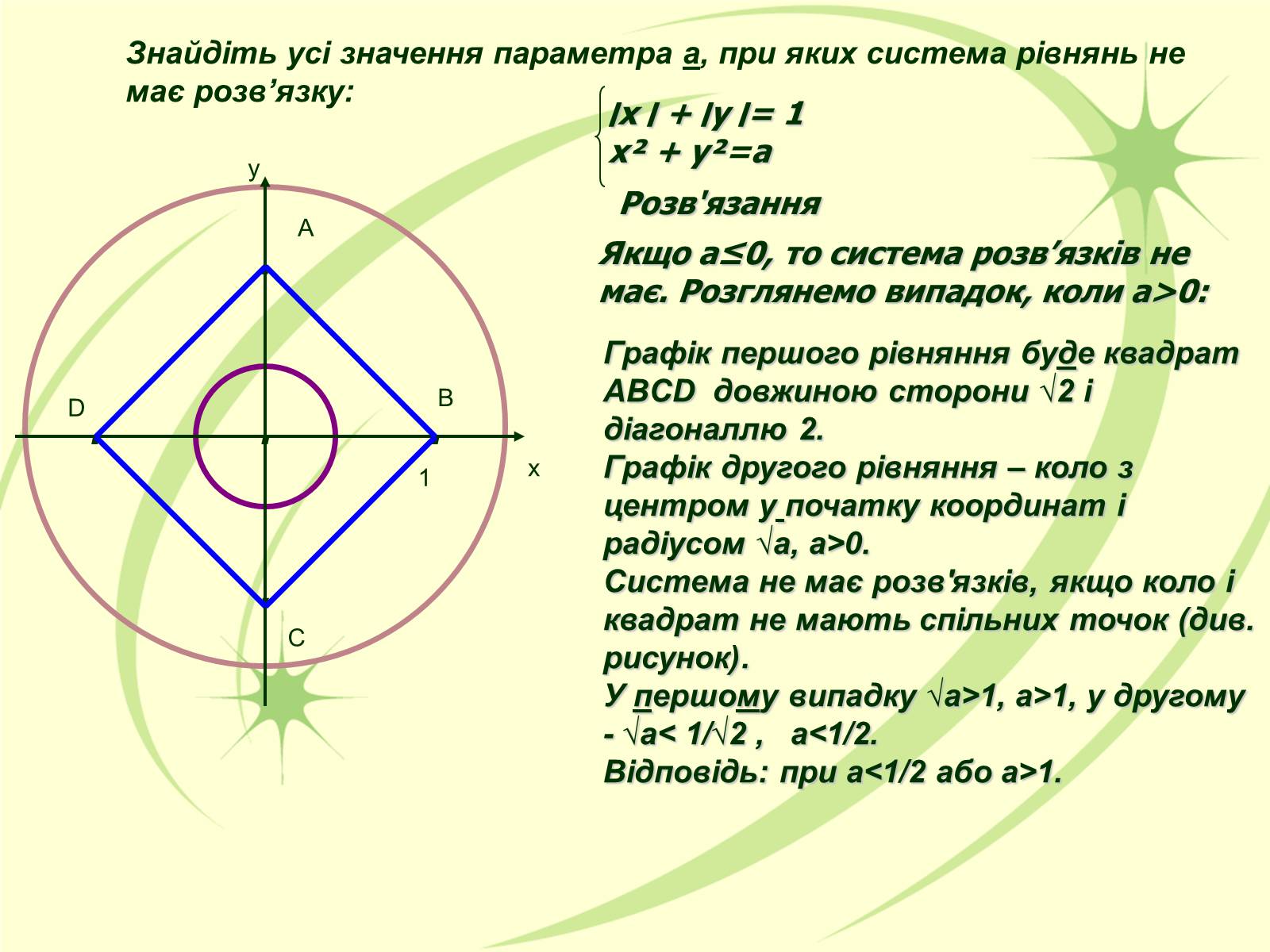
Знайдіть усі значення параметра а, при яких система рівнянь не має розв'язку:
.
.
.
.
.
B
׀х ׀ + ׀у ׀= 1
х² + у²=а
Розв'язання
Якщо а≤0, то система розв'язків не має. Розглянемо випадок, коли а>0:
Графік першого рівняння буде квадрат ABCD довжиною сторони √2 і діагоналлю 2.
Графік другого рівняння – коло з центром у початку координат і радіусом √а, а>0.
Система не має розв'язків, якщо коло і квадрат не мають спільних точок (див. рисунок).
У першому випадку √а>1, а>1, у другому - √а< 1/√2 , а<1/2.
Відповідь: при а<1/2 або а>1.
C
A
D
у
х
1
.
.
.
.
.
B
׀х ׀ + ׀у ׀= 1
х² + у²=а
Розв'язання
Якщо а≤0, то система розв'язків не має. Розглянемо випадок, коли а>0:
Графік першого рівняння буде квадрат ABCD довжиною сторони √2 і діагоналлю 2.
Графік другого рівняння – коло з центром у початку координат і радіусом √а, а>0.
Система не має розв'язків, якщо коло і квадрат не мають спільних точок (див. рисунок).
У першому випадку √а>1, а>1, у другому - √а< 1/√2 , а<1/2.
Відповідь: при а<1/2 або а>1.
C
A
D
у
х
1
Слайд #9
.
.
.
у=а
у=׀х²-6 ׀х׀+8 ׀
Графіком першого рівняння буде пряма паралельна осі х;
Графіком другого рівняння буде парабола,зміщена на три одиниці вправо по осі х та на одиницю вниз по осі у, і відображена відносно осі у та х по модулю. Тобто:
у= |x²-6х+8->у=(x-2)(x-4)->y=(x-3)²-1
Отже
при а<0, розв'язків немає;
при а=0, 4 розв'язки;
при 0<а<1, 8 розв'язків;
при а=1, 6 розв'язків;
при 1<а<8, 4 розв'язки;
при а=8, 3 розв'язки;
при а>8, 2 розв'язки.
1
Знайдіть усі значення параметра а, при яких система рівнянь має розв'язки:
у=а
y=(x-3)²-1
.
.
.
1
.
8
.
3
.
у
х
.
3
.
.
.
.
у=а
у=׀х²-6 ׀х׀+8 ׀
Графіком першого рівняння буде пряма паралельна осі х;
Графіком другого рівняння буде парабола,зміщена на три одиниці вправо по осі х та на одиницю вниз по осі у, і відображена відносно осі у та х по модулю. Тобто:
у= |x²-6х+8->у=(x-2)(x-4)->y=(x-3)²-1
Отже
при а<0, розв'язків немає;
при а=0, 4 розв'язки;
при 0<а<1, 8 розв'язків;
при а=1, 6 розв'язків;
при 1<а<8, 4 розв'язки;
при а=8, 3 розв'язки;
при а>8, 2 розв'язки.
1
Знайдіть усі значення параметра а, при яких система рівнянь має розв'язки:
у=а
y=(x-3)²-1
.
.
.
1
.
8
.
3
.
у
х
.
3
.
.

Слайд #10
Знайдіть кількість розв'язків відносно параметра а:
.
.
.
.
.
׀х ׀ + ׀у ׀= 1
х²+у²=а²
Якщо а≤0, то система розв'язків не має. Розглянемо випадок, коли а>0:
Графік першого рівняння буде квадрат ABCD з довжиною сторони √2, і при перетині його з осями координат утвориться 4 прямокутних рівнобедрених трикутника, висота кожного з них дорівнює радіусу вписаного кола ( якщо б коло дотикалось до сторони квадрата ), то знайдемо довжину радіуса кола, при дотику, або висоту трикутника:
х²+у²=а²=> х²+у²=r²=> r²=а²=> √r²=√а² => r=|a|.
1. АВ²=1²+1², АВ= √2;
2. Висота і медіана у прямокутному рівнобедреному трикутнику дорівнює половині гіпотенузи, тому висота і медіана дорівнюють √2/2 або 1/√2 ;
Оскільки висота і медіана в прямокутному рівнобедреному трикутнику дорівнюють радіусу кола при дотику, то r=a=1/√2;
Тому маємо 5 випадків:
1) a< 1/√2, немає розв'язків;
2) а= 1/√2, 4 розв'язки;
3) 1/√24) a=1, 4 розв'язки;
5) a>1, немає розв'язків.
х
1
C
A
D
B
у
.
.
.
.
.
׀х ׀ + ׀у ׀= 1
х²+у²=а²
Якщо а≤0, то система розв'язків не має. Розглянемо випадок, коли а>0:
Графік першого рівняння буде квадрат ABCD з довжиною сторони √2, і при перетині його з осями координат утвориться 4 прямокутних рівнобедрених трикутника, висота кожного з них дорівнює радіусу вписаного кола ( якщо б коло дотикалось до сторони квадрата ), то знайдемо довжину радіуса кола, при дотику, або висоту трикутника:
х²+у²=а²=> х²+у²=r²=> r²=а²=> √r²=√а² => r=|a|.
1. АВ²=1²+1², АВ= √2;
2. Висота і медіана у прямокутному рівнобедреному трикутнику дорівнює половині гіпотенузи, тому висота і медіана дорівнюють √2/2 або 1/√2 ;
Оскільки висота і медіана в прямокутному рівнобедреному трикутнику дорівнюють радіусу кола при дотику, то r=a=1/√2;
Тому маємо 5 випадків:
1) a< 1/√2, немає розв'язків;
2) а= 1/√2, 4 розв'язки;
3) 1/√2
5) a>1, немає розв'язків.
х
1
C
A
D
B
у

Слайд #11
.
.
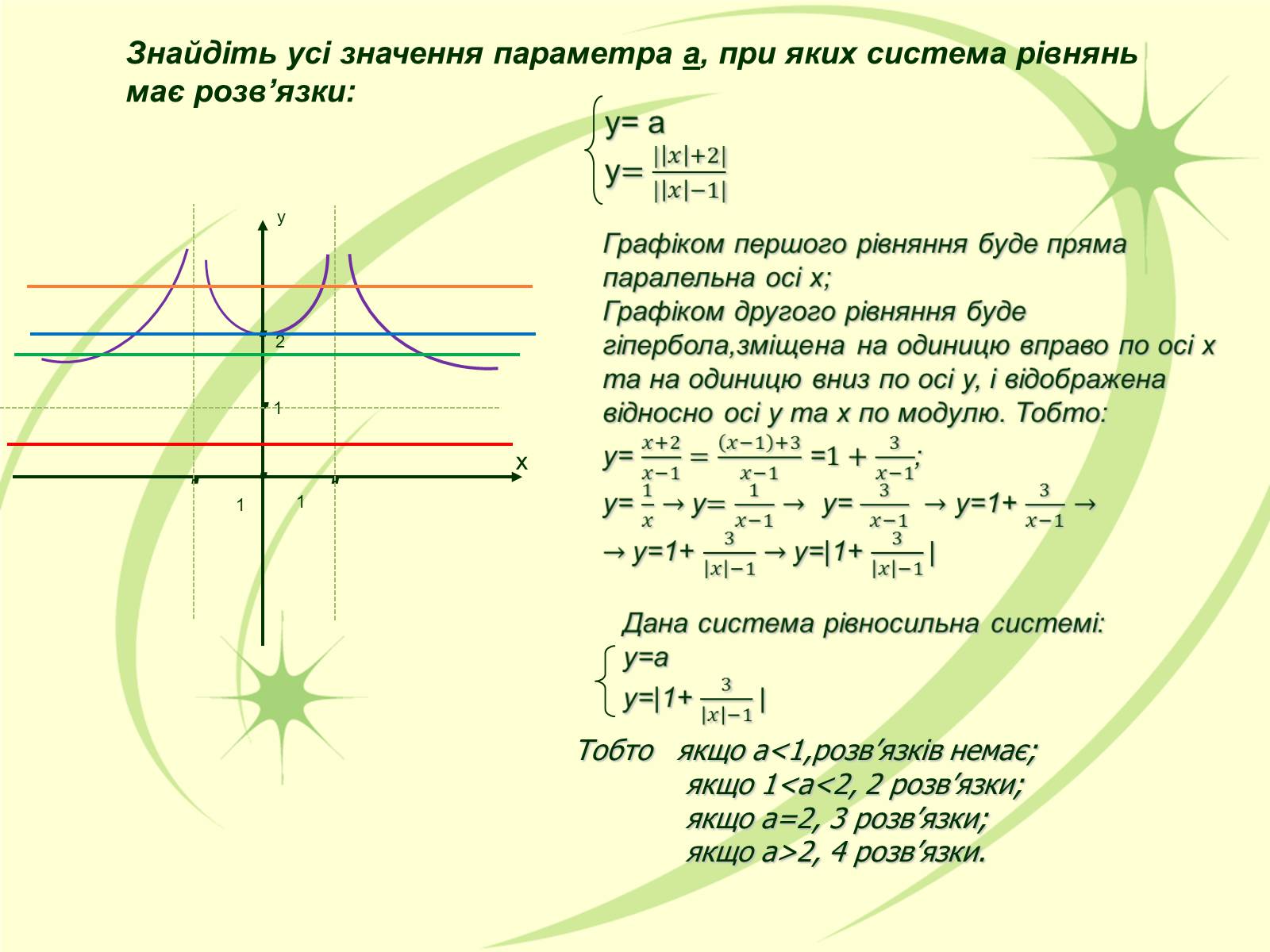
Тобто якщо а<1,розв'язків немає;
якщо 1якщо а=2, 3 розв'язки;
якщо а>2, 4 розв'язки.
1
Знайдіть усі значення параметра а, при яких система рівнянь має розв'язки:
1
.
.
.
2
х
y
1
.
Тобто якщо а<1,розв'язків немає;
якщо 1
якщо а>2, 4 розв'язки.
1
Знайдіть усі значення параметра а, при яких система рівнянь має розв'язки:
1
.
.
.
2
х
y
1
Слайд #12
Скільки розв'язків має система відносно параметра а:
.
.
.
х²+у²+4х=0
х²+у²-2х=а²-2а
Перетворимо дані рівняння системи:
Тому маємо 5 випадків:
1) a>3, немає розв'язків;
2) а=3, 1 розв'язок;
3) 14) a=1, 1 розв'язок;
5) a<1, немає розв'язків.
у
х
1
2
.
.
.
х²+у²+4х=0
х²+у²-2х=а²-2а
Перетворимо дані рівняння системи:
Тому маємо 5 випадків:
1) a>3, немає розв'язків;
2) а=3, 1 розв'язок;
3) 1
5) a<1, немає розв'язків.
у
х
1
2

Слайд #13
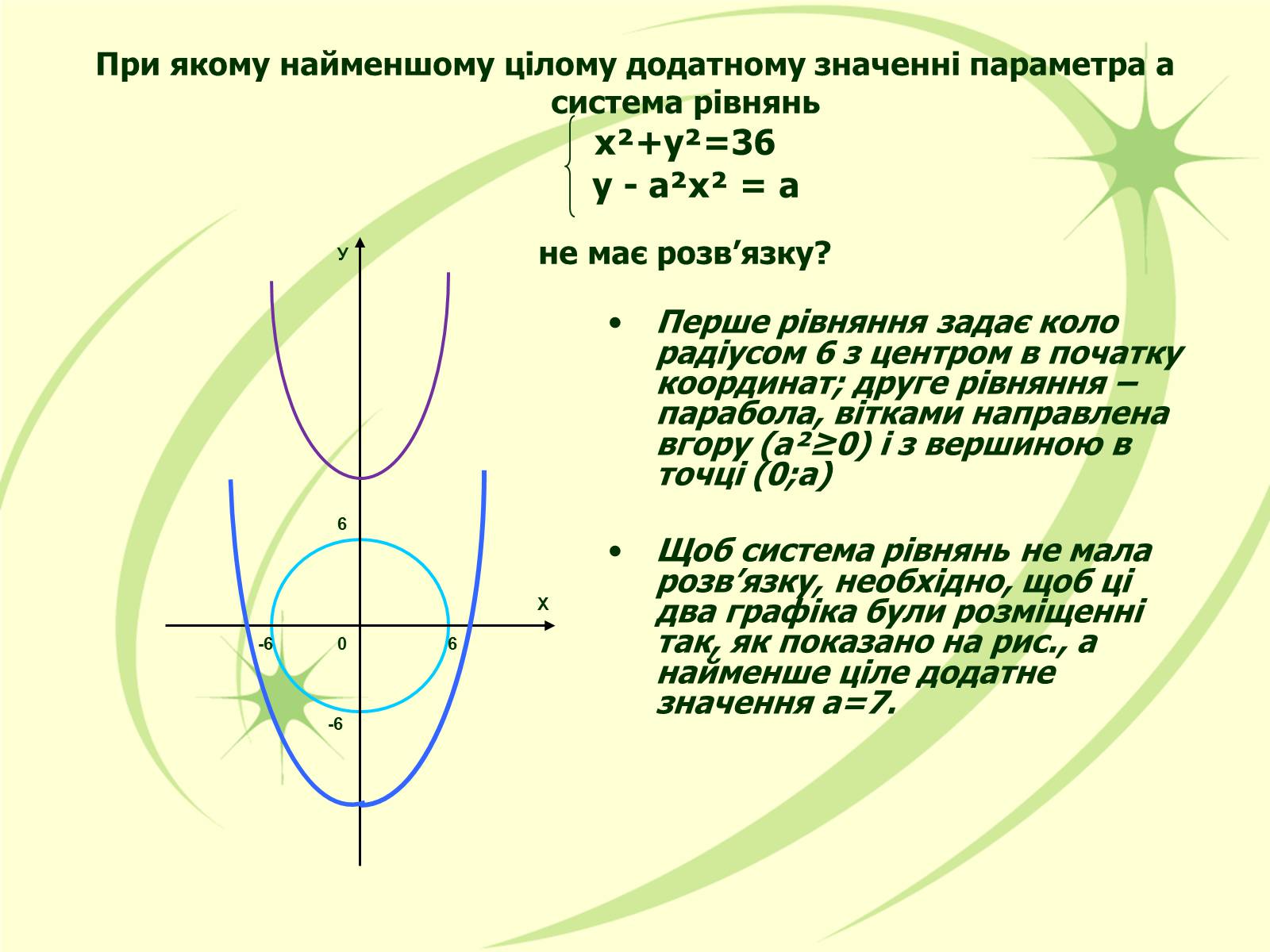
При якому найменшому цілому додатному значенні параметра а система рівняньх²+у²=36 у - а²х² = а не має розв'язку?
Перше рівняння задає коло радіусом 6 з центром в початку координат; друге рівняння – парабола, вітками направлена вгору (а²≥0) і з вершиною в точці (0;а)
Щоб система рівнянь не мала розв'язку, необхідно, щоб ці два графіка були розміщенні так, як показано на рис., а найменше ціле додатне значення а=7.
У
Х
6
6
-6
-6
Перше рівняння задає коло радіусом 6 з центром в початку координат; друге рівняння – парабола, вітками направлена вгору (а²≥0) і з вершиною в точці (0;а)
Щоб система рівнянь не мала розв'язку, необхідно, щоб ці два графіка були розміщенні так, як показано на рис., а найменше ціле додатне значення а=7.
У
Х
6
6
-6
-6
Слайд #14
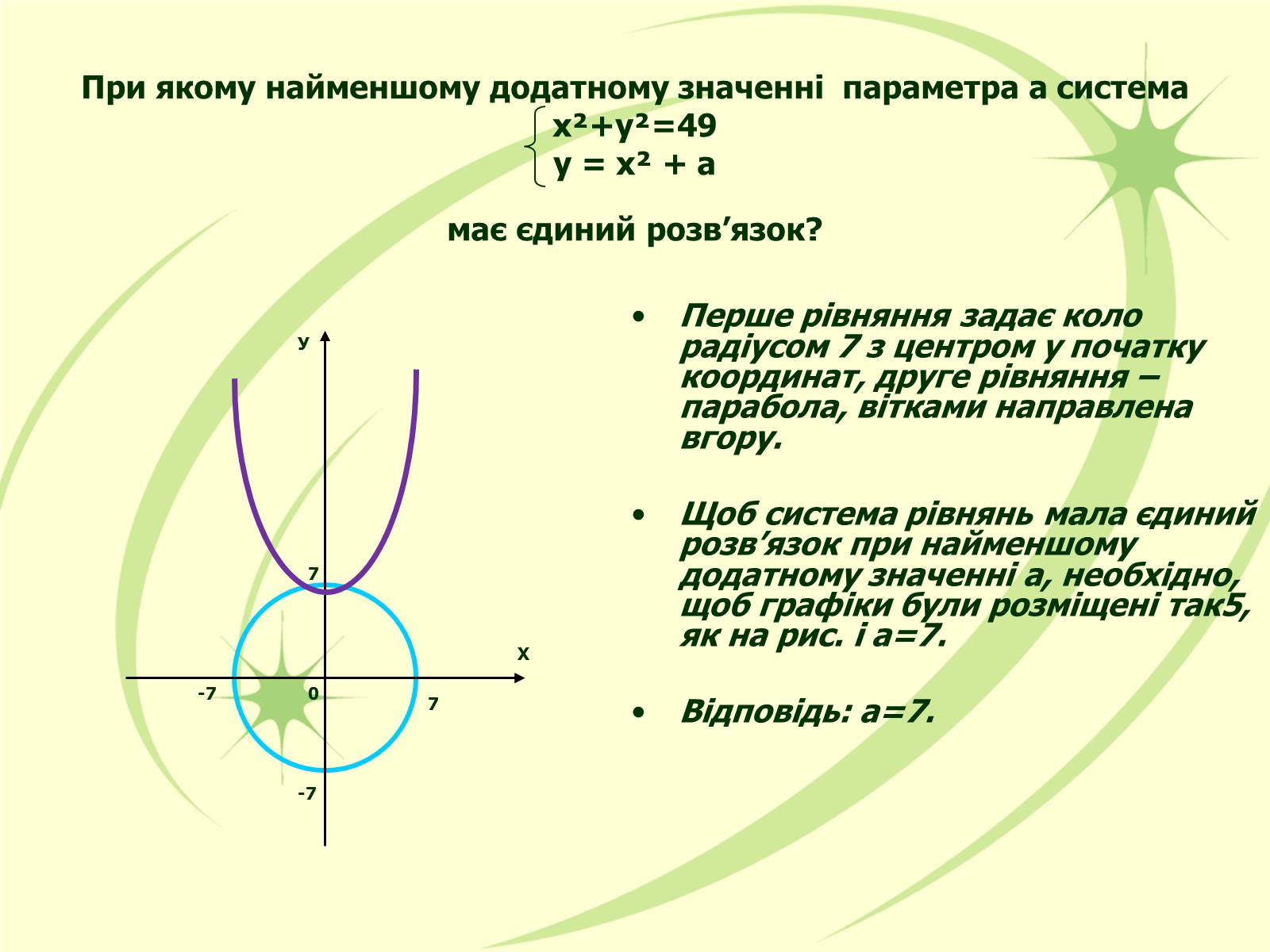
При якому найменшому додатному значенні параметра а система х²+у²=49у = х² + амає єдиний розв'язок?
Перше рівняння задає коло радіусом 7 з центром у початку координат, друге рівняння – парабола, вітками направлена вгору.
Щоб система рівнянь мала єдиний розв'язок при найменшому додатному значенні а, необхідно, щоб графіки були розміщені так5, як на рис. і а=7.
Відповідь: а=7.
7
7
-7
-7
Х
У
Перше рівняння задає коло радіусом 7 з центром у початку координат, друге рівняння – парабола, вітками направлена вгору.
Щоб система рівнянь мала єдиний розв'язок при найменшому додатному значенні а, необхідно, щоб графіки були розміщені так5, як на рис. і а=7.
Відповідь: а=7.
7
7
-7
-7
Х
У
Слайд #15
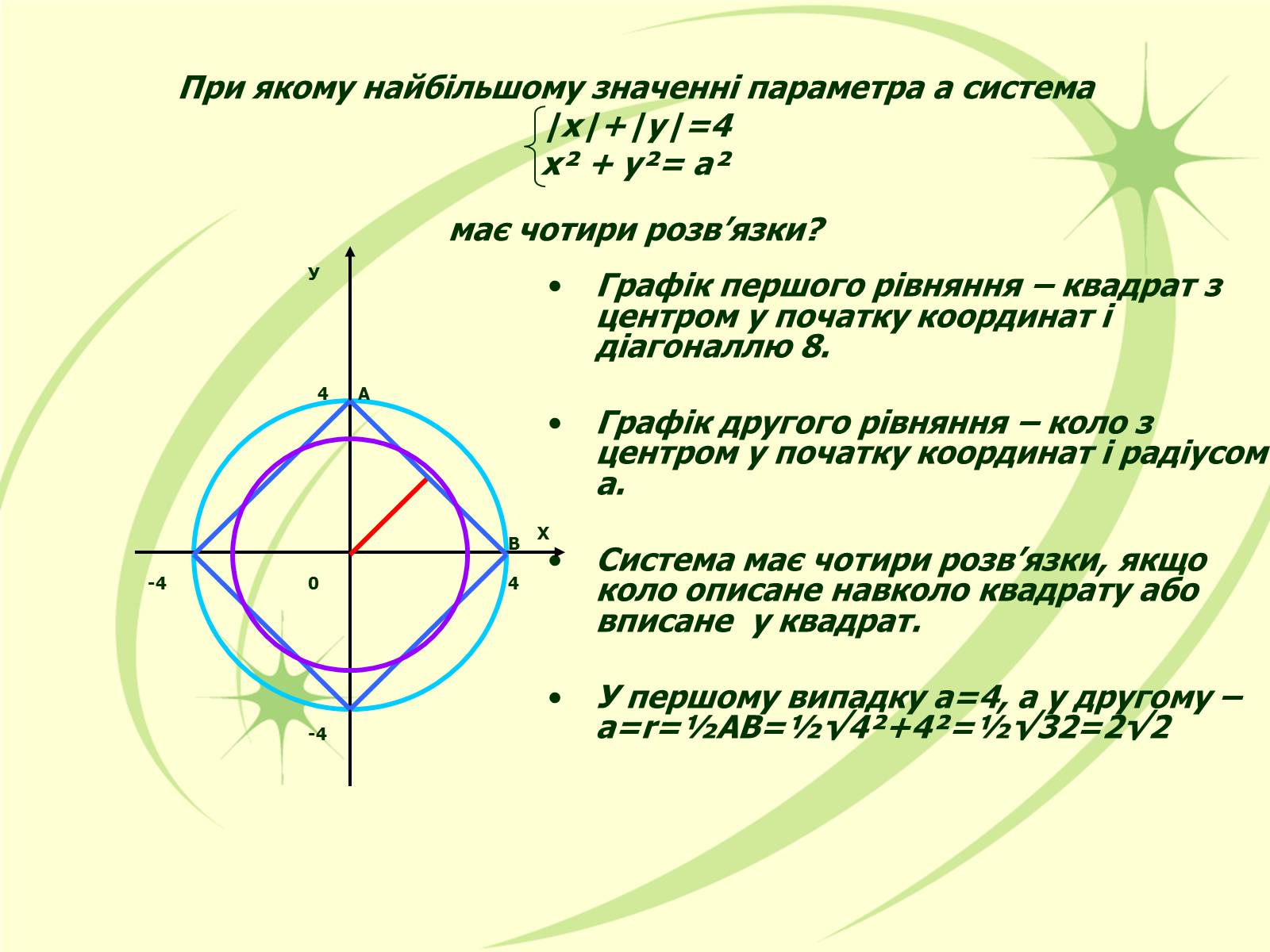
При якому найбільшому значенні параметра а система|x|+|y|=4х² + у²= а²має чотири розв'язки?
Графік першого рівняння – квадрат з центром у початку координат і діагоналлю 8.
Графік другого рівняння – коло з центром у початку координат і радіусом а.
Система має чотири розв'язки, якщо коло описане навколо квадрату або вписане у квадрат.
У першому випадку а=4, а у другому – а=r=½AB=½√4²+4²=½√32=2√2
У
Х
4
4
-4
-4
А
В
Графік першого рівняння – квадрат з центром у початку координат і діагоналлю 8.
Графік другого рівняння – коло з центром у початку координат і радіусом а.
Система має чотири розв'язки, якщо коло описане навколо квадрату або вписане у квадрат.
У першому випадку а=4, а у другому – а=r=½AB=½√4²+4²=½√32=2√2
У
Х
4
4
-4
-4
А
В
Слайд #16
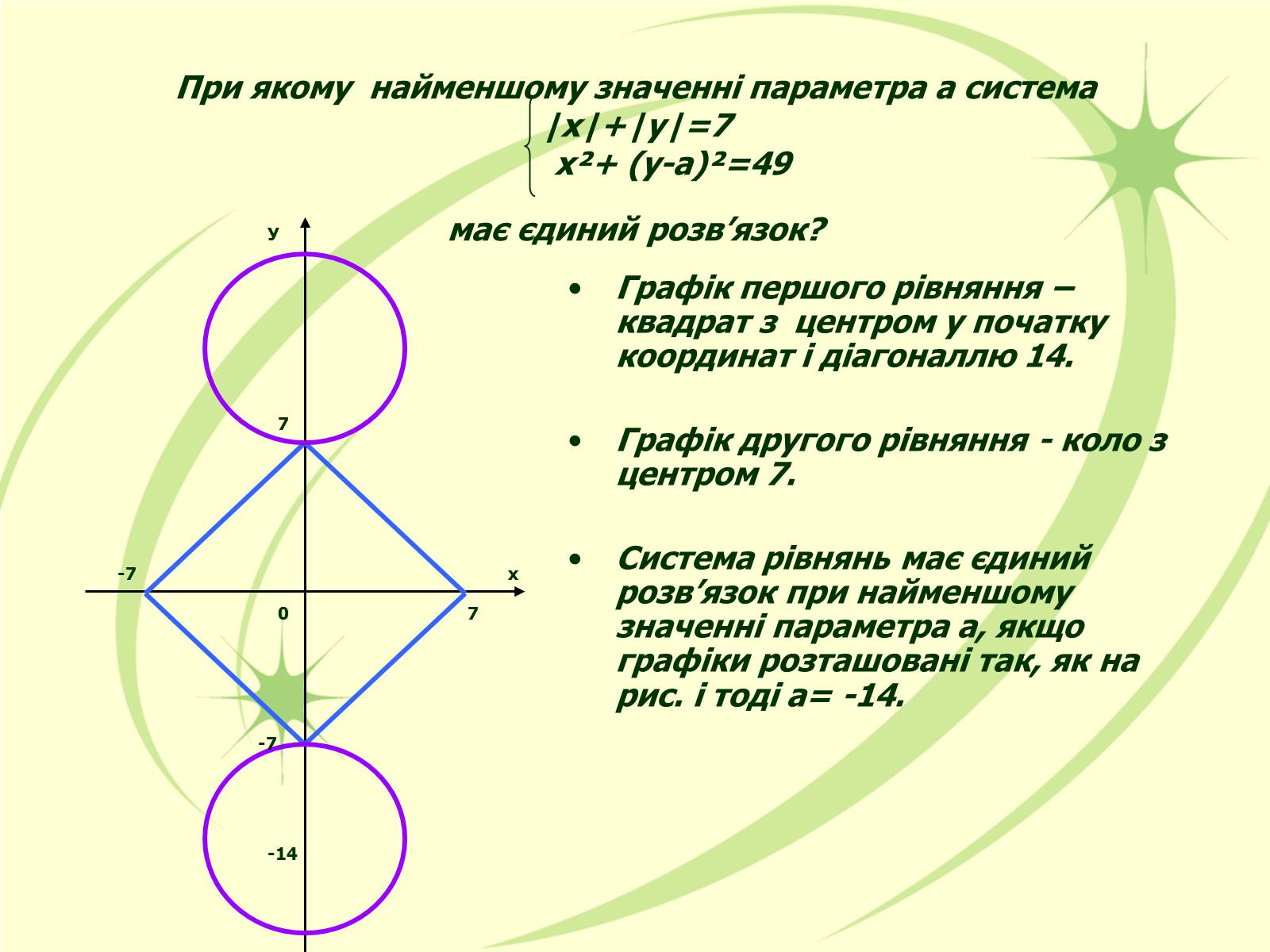
При якому найменшому значенні параметра а система |x|+|y|=7 х²+ (у-а)²=49має єдиний розв'язок?
Графік першого рівняння – квадрат з центром у початку координат і діагоналлю 14.
Графік другого рівняння - коло з центром 7.
Система рівнянь має єдиний розв'язок при найменшому значенні параметра а, якщо графіки розташовані так, як на рис. і тоді а= -14.
У
х
7
7
-7
-7
-14
Графік першого рівняння – квадрат з центром у початку координат і діагоналлю 14.
Графік другого рівняння - коло з центром 7.
Система рівнянь має єдиний розв'язок при найменшому значенні параметра а, якщо графіки розташовані так, як на рис. і тоді а= -14.
У
х
7
7
-7
-7
-14