- Головна
- Готові шкільні презентації
- Презентація на тему «Практичне застосування інтегралів в економіці. Прикладні задачі.»
Презентація на тему «Практичне застосування інтегралів в економіці. Прикладні задачі.»
271
Слайд #1
Практичне застосування інтегралів в економіці. Прикладні задачі.
Підготувала
учениця 11-а класу
Кошина Анна
Підготувала
учениця 11-а класу
Кошина Анна

Слайд #2
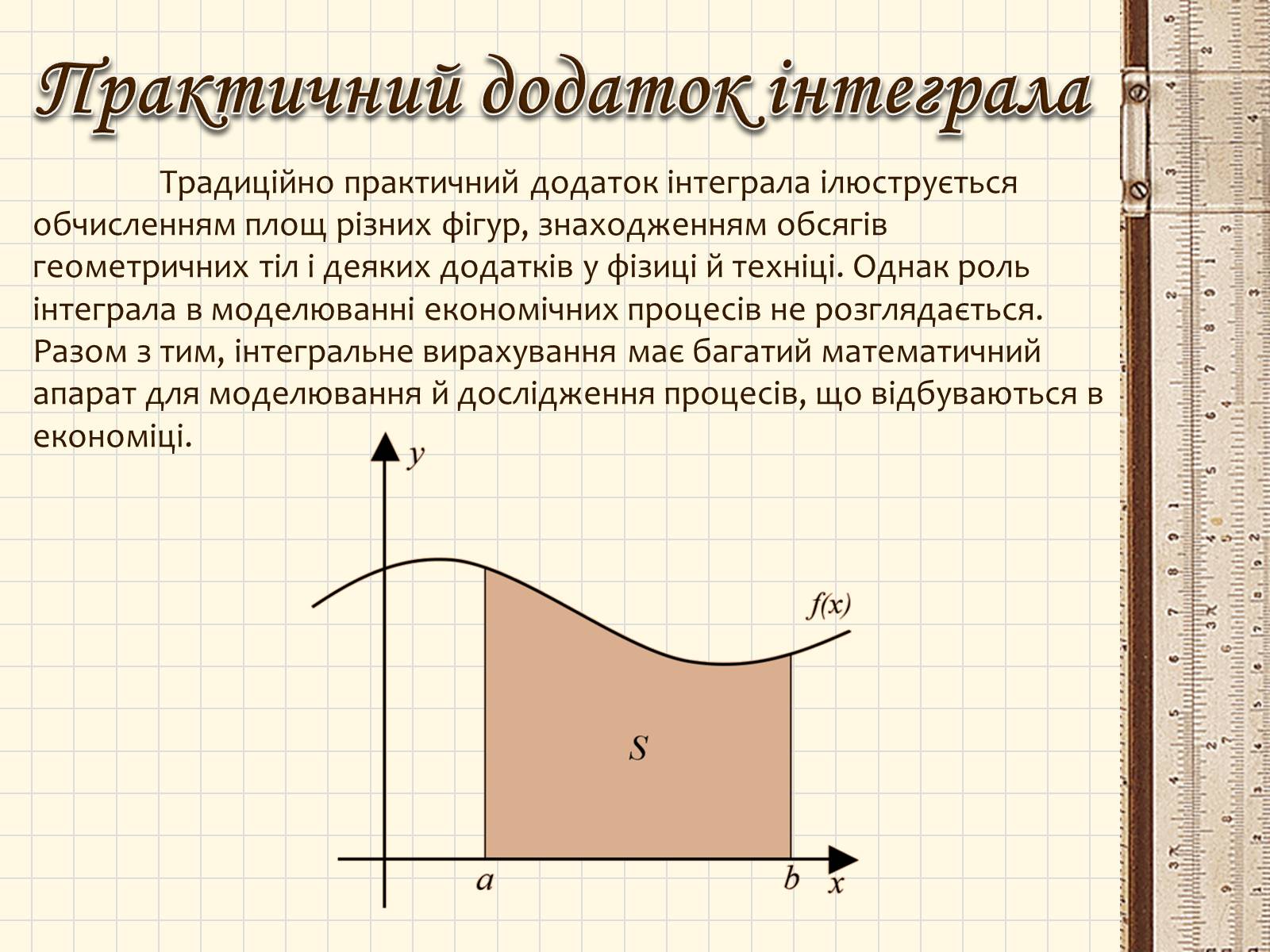
Традиційно практичний додаток інтеграла ілюструється обчисленням площ різних фігур, знаходженням обсягів геометричних тіл і деяких додатків у фізиці й техніці. Однак роль інтеграла в моделюванні економічних процесів не розглядається. Разом з тим, інтегральне вирахування має багатий математичний апарат для моделювання й дослідження процесів, що відбуваються в економіці.
Практичний додаток інтеграла
Практичний додаток інтеграла
Слайд #3
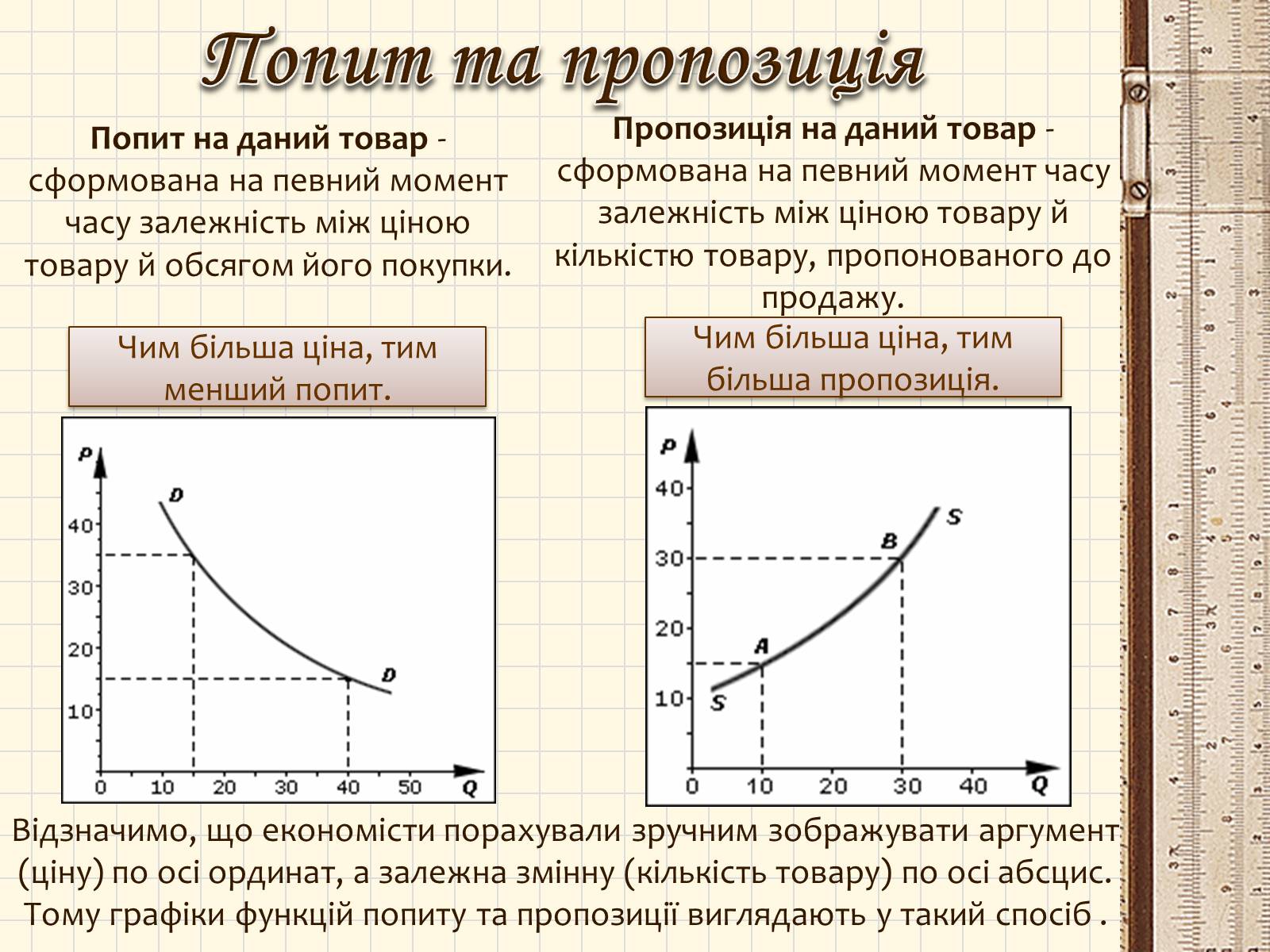
Попит на даний товар - сформована на певний момент часу залежність між ціною товару й обсягом його покупки.
Попит та пропозиція
Пропозиція на даний товар - сформована на певний момент часу залежність між ціною товару й кількістю товару, пропонованого до продажу.
Чим більша ціна, тим менший попит.
Чим більша ціна, тим більша пропозиція.
Відзначимо, що економісти порахували зручним зображувати аргумент (ціну) по осі ординат, а залежна змінну (кількість товару) по осі абсцис. Тому графіки функцій попиту та пропозиції виглядають у такий спосіб .
Попит та пропозиція
Пропозиція на даний товар - сформована на певний момент часу залежність між ціною товару й кількістю товару, пропонованого до продажу.
Чим більша ціна, тим менший попит.
Чим більша ціна, тим більша пропозиція.
Відзначимо, що економісти порахували зручним зображувати аргумент (ціну) по осі ординат, а залежна змінну (кількість товару) по осі абсцис. Тому графіки функцій попиту та пропозиції виглядають у такий спосіб .
Слайд #4
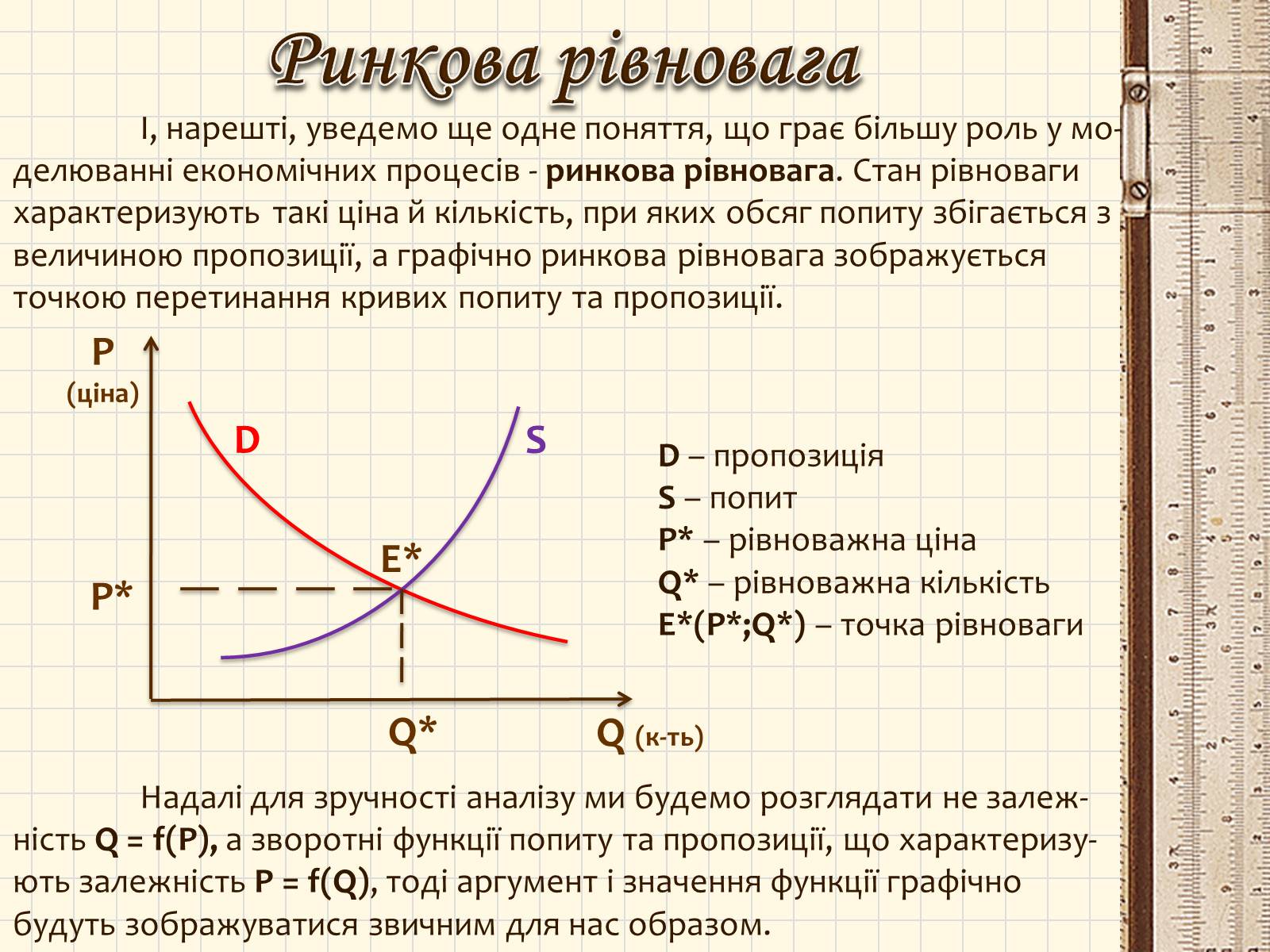
І, нарешті, уведемо ще одне поняття, що грає більшу роль у мо-делюванні економічних процесів - ринкова рівновага. Стан рівноваги характеризують такі ціна й кількість, при яких обсяг попиту збігається з величиною пропозиції, а графічно ринкова рівновага зображується точкою перетинання кривих попиту та пропозиції.
Ринкова рівновага
P
(ціна)
Q (к-ть)
P*
Q*
E*
S
D
D – пропозиція
S – попит
P* – рівноважна ціна
Q* – рівноважна кількість
E*(P*;Q*) – точка рівноваги
Надалі для зручності аналізу ми будемо розглядати не залеж-ність Q = f(P), а зворотні функції попиту та пропозиції, що характеризу-ють залежність P = f(Q), тоді аргумент і значення функції графічно будуть зображуватися звичним для нас образом.
Ринкова рівновага
P
(ціна)
Q (к-ть)
P*
Q*
E*
S
D
D – пропозиція
S – попит
P* – рівноважна ціна
Q* – рівноважна кількість
E*(P*;Q*) – точка рівноваги
Надалі для зручності аналізу ми будемо розглядати не залеж-ність Q = f(P), а зворотні функції попиту та пропозиції, що характеризу-ють залежність P = f(Q), тоді аргумент і значення функції графічно будуть зображуватися звичним для нас образом.
Слайд #5
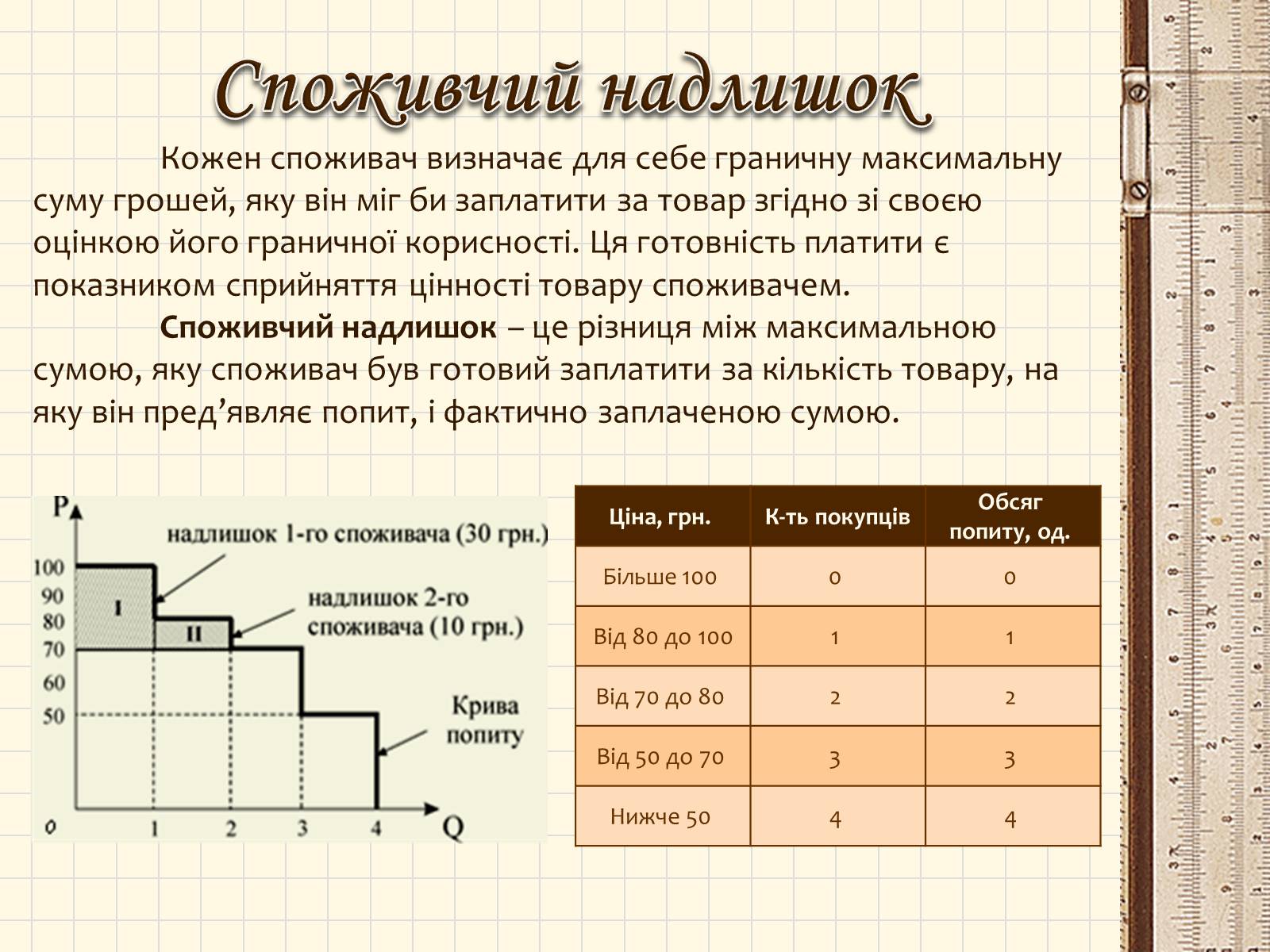
Кожен споживач визначає для себе граничну максимальну суму грошей, яку він міг би заплатити за товар згідно зі своєю оцінкою його граничної корисності. Ця готовність платити є показником сприйняття цінності товару споживачем.
Споживчий надлишок – це різниця між максимальною сумою, яку споживач був готовий заплатити за кількість товару, на яку він пред'являє попит, і фактично заплаченою сумою.
Споживчий надлишок
Ціна, грн.
К-ть покупців
Обсяг попиту, од.
Більше 100
0
0
Від 80 до 100
1
1
Від 70 до 80
2
2
Від 50 до 70
3
3
Нижче 50
4
4
Споживчий надлишок – це різниця між максимальною сумою, яку споживач був готовий заплатити за кількість товару, на яку він пред'являє попит, і фактично заплаченою сумою.
Споживчий надлишок
Ціна, грн.
К-ть покупців
Обсяг попиту, од.
Більше 100
0
0
Від 80 до 100
1
1
Від 70 до 80
2
2
Від 50 до 70
3
3
Нижче 50
4
4
Слайд #6
Перейдемо тепер до розгляду додатків інтегрального аналізу для визначення споживчого надлишку. Для цього зобразимо на графіку зворотну функцію попиту P = f(Q). Допустимо, що ринкова рівновага встановилася в точці E*(q*; p*) (крива пропозиції на графіку відсутній для зручності подальшого аналізу).
Якщо покупець здобуває товар у кількості Q* за рівноважною ціною P*, то очевидно, що загальні витрати на покупку такого товару складуть P*Q*, що дорівнює площі заштрихованої фігури A.
Визначення споживчого надлишку
P
Q
P*
Q*
E*(Q*; P*)
D
A
Якщо покупець здобуває товар у кількості Q* за рівноважною ціною P*, то очевидно, що загальні витрати на покупку такого товару складуть P*Q*, що дорівнює площі заштрихованої фігури A.
Визначення споживчого надлишку
P
Q
P*
Q*
E*(Q*; P*)
D
A

Слайд #7
Але припустимо тепер, що товар у кількості Q* продається продавцями не відразу, а надходить на ринок невеликими партіями Q. Саме таке допущення разом із припущенням про безперервність функції попиту та пропозиції є основним при висновку формули для розрахунку споживчого надлишку. Відзначимо, що дане допущення цілком виправдане, тому що така схема реалізації товару досить поширена на практиці й випливає з мети продавця підтримувати ціну на товар якнайвище.
Визначення споживчого надлишку
Визначення споживчого надлишку

Слайд #8
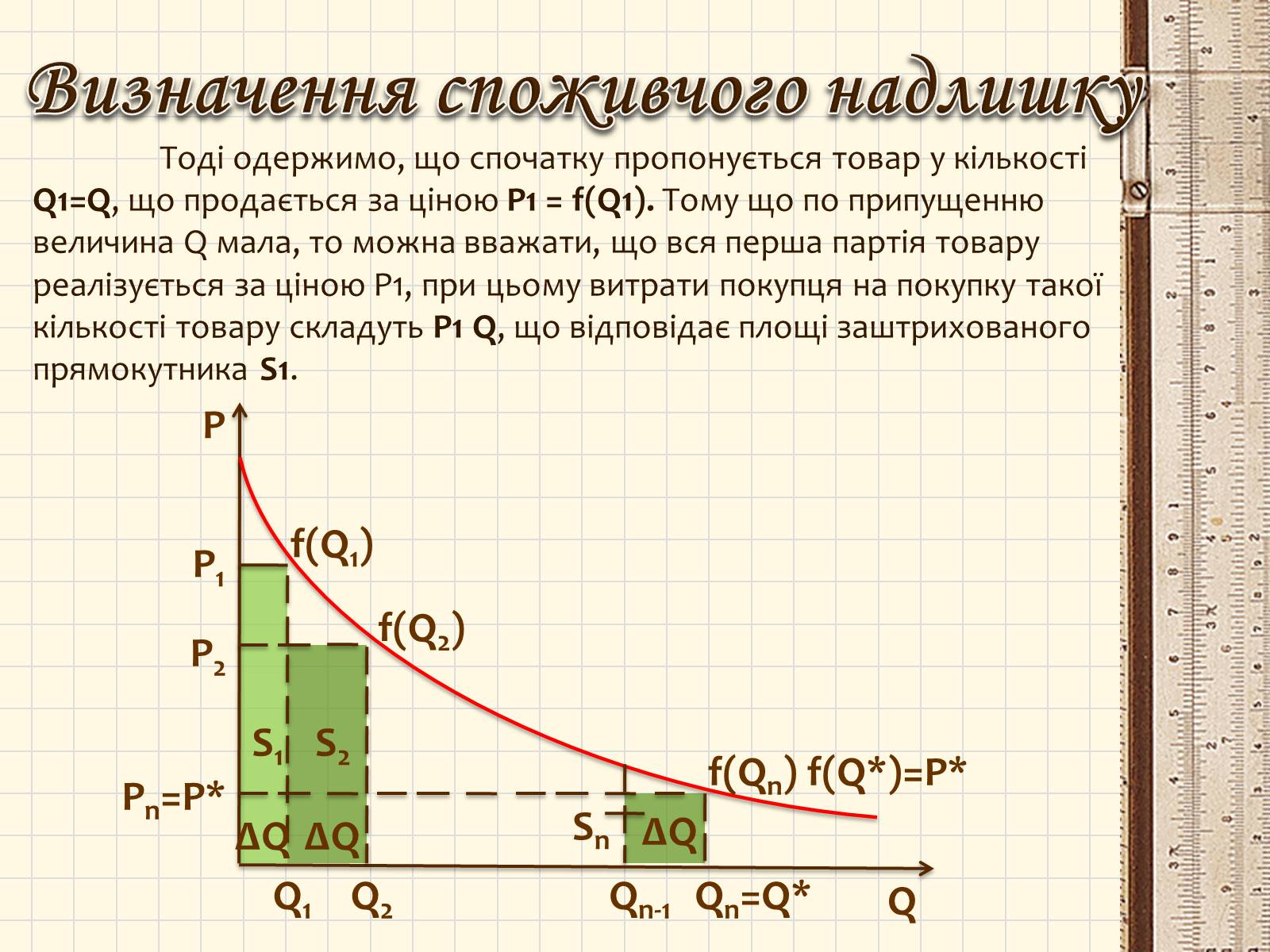
Тоді одержимо, що спочатку пропонується товар у кількості Q1=Q, що продається за ціною P1 = f(Q1). Тому що по припущенню величина Q мала, то можна вважати, що вся перша партія товару реалізується за ціною P1, при цьому витрати покупця на покупку такої кількості товару складуть P1 Q, що відповідає площі заштрихованого прямокутника S1.
Q1
Qn-1
Qn=Q*
P
Q
Pn=P*
Q2
P1
P2
∆Q
∆Q
∆Q
f(Q1)
f(Q2)
f(Qn) f(Q*)=P*
S1
S2
Sn
Визначення споживчого надлишку
Q1
Qn-1
Qn=Q*
P
Q
Pn=P*
Q2
P1
P2
∆Q
∆Q
∆Q
f(Q1)
f(Q2)
f(Qn) f(Q*)=P*
S1
S2
Sn
Визначення споживчого надлишку
Слайд #9
Далі на ринок надходить друга партія товару в тій же кількості, що продається за ціною
P2 = f(Q2), де Q2 = Q1+Q
– загальна кількість реалізованої продукції, а витрати покупця на покупку другої партії складуть P2Q, що відповідає площі прямокутника S2.
Продовжимо процес доти, поки не дійдемо до рівноважної кількості товару Q* = Qn. Тоді стає ясно, якою повинна бути величина Q для того, щоб процес продажу товару закінчився в крапці Q*:
У результаті одержимо, що ціна n-й партії товару Pn = f(Qn) = f(Q*) = P*, а витрати споживачів на покупку цієї останньої партії товару складуть PnQ, або площа прямокутника Sn.
Визначення споживчого надлишку
P2 = f(Q2), де Q2 = Q1+Q
– загальна кількість реалізованої продукції, а витрати покупця на покупку другої партії складуть P2Q, що відповідає площі прямокутника S2.
Продовжимо процес доти, поки не дійдемо до рівноважної кількості товару Q* = Qn. Тоді стає ясно, якою повинна бути величина Q для того, щоб процес продажу товару закінчився в крапці Q*:
У результаті одержимо, що ціна n-й партії товару Pn = f(Qn) = f(Q*) = P*, а витрати споживачів на покупку цієї останньої партії товару складуть PnQ, або площа прямокутника Sn.
Визначення споживчого надлишку

Слайд #10
Таким чином, ми одержимо, що сумарні витрати споживачів при покупці товару дрібними партіями Q рівні Q.
P1∆Q + P2∆Q + …+ Pn∆Q =
= f(Q1)∆Q + f(Q2)∆Q +…+ f(Qn)∆Q =
= S1 + S2 +…+ Sn
Тому що величина Q дуже мала, а функція f(Q) безперервна, тих містимо, що S1 + S2 +…+ Sn приблизно дорівнює площі фігури B, що, як відомо, при малих збільшеннях аргументу Q дорівнює певному інтегралу від зворотної функції попиту при зміні аргументу від 0 до Q*, тобто в підсумку одержимо, що
P
Q
P*
Q*
E*(Q*; P*)
D
B
Визначення споживчого надлишку
P1∆Q + P2∆Q + …+ Pn∆Q =
= f(Q1)∆Q + f(Q2)∆Q +…+ f(Qn)∆Q =
= S1 + S2 +…+ Sn
Тому що величина Q дуже мала, а функція f(Q) безперервна, тих містимо, що S1 + S2 +…+ Sn приблизно дорівнює площі фігури B, що, як відомо, при малих збільшеннях аргументу Q дорівнює певному інтегралу від зворотної функції попиту при зміні аргументу від 0 до Q*, тобто в підсумку одержимо, що
P
Q
P*
Q*
E*(Q*; P*)
D
B
Визначення споживчого надлишку

Слайд #11
Згадавши, що кожна точка на кривій попиту показує, яку суму споживач готовий заплатити за покупку додаткової одиниці продукту, одержимо, що площа фігури B відповідає загальній грошовій сумі, що споживач готовий витратити на покупку Q* одиниць товару. Тоді
SВ - SА = SCS
– споживчий надлишок при покупці даного товару - перевищення загальної вартості, що споживач готовий сплатити за всі одиниці товару, над його реальними витратами на їхнє придбання.
P
Q
P*
Q*
E*(Q*; P*)
D
CS
Визначення споживчого надлишку
P
Q
P*
Q*
E*(Q*; P*)
D
B
P
Q
P*
Q*
E*(Q*; P*)
D
A
SВ - SА = SCS
– споживчий надлишок при покупці даного товару - перевищення загальної вартості, що споживач готовий сплатити за всі одиниці товару, над його реальними витратами на їхнє придбання.
P
Q
P*
Q*
E*(Q*; P*)
D
CS
Визначення споживчого надлишку
P
Q
P*
Q*
E*(Q*; P*)
D
B
P
Q
P*
Q*
E*(Q*; P*)
D
A

Слайд #12
Таким чином, споживчий надлишок можна порахувати за наступною формулою
Визначення споживчого надлишку
CS – споживчий надлишок
f(Q) – функція попиту
P* – рівноважна ціна
Q* – рівноважна кількість
Визначення споживчого надлишку
CS – споживчий надлишок
f(Q) – функція попиту
P* – рівноважна ціна
Q* – рівноважна кількість

Слайд #13
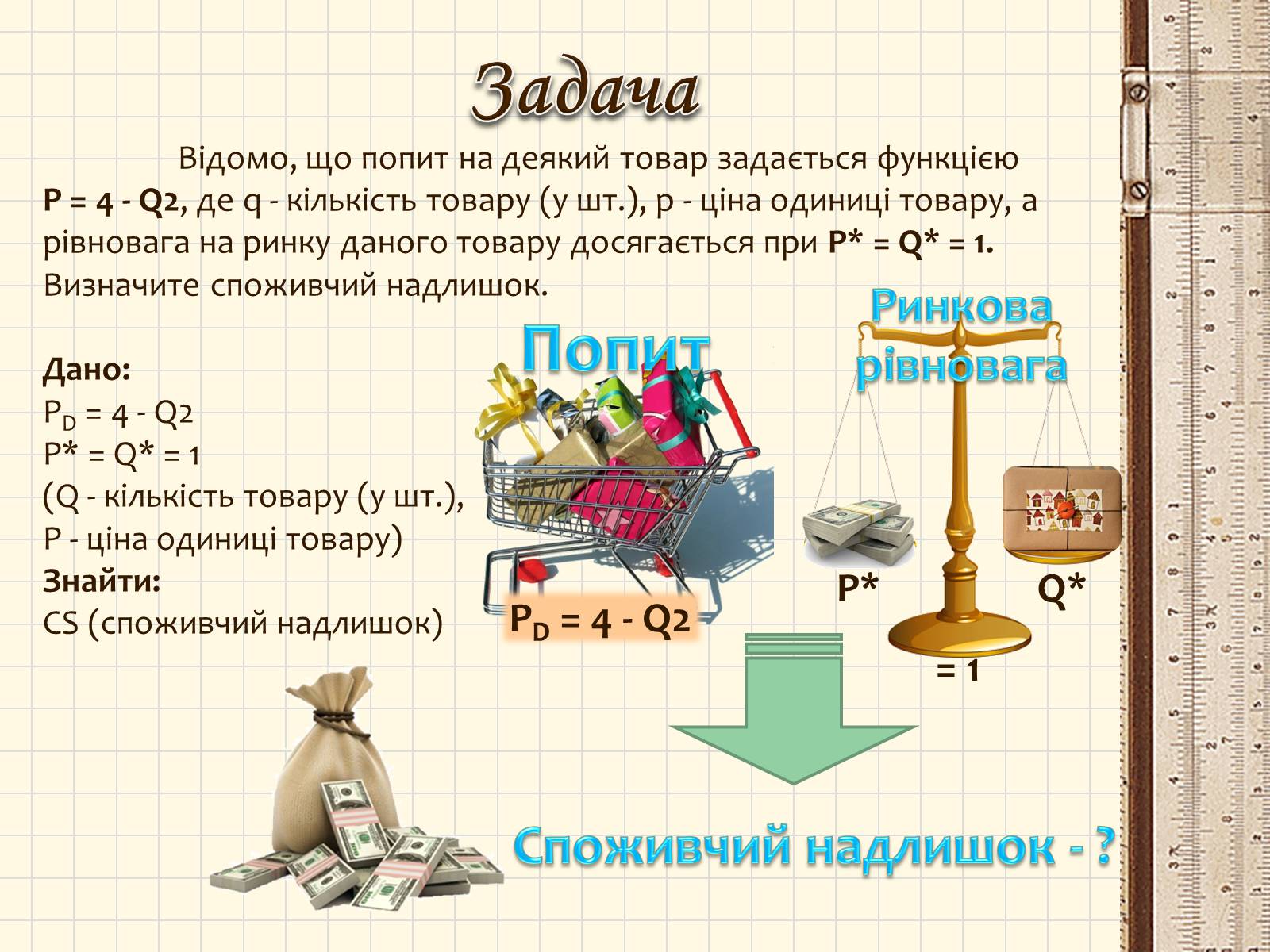
Відомо, що попит на деякий товар задається функцією P = 4 - Q2, де q - кількість товару (у шт.), p - ціна одиниці товару, а рівновага на ринку даного товару досягається при P* = Q* = 1. Визначите споживчий надлишок.
Дано:
PD = 4 - Q2
P* = Q* = 1
(Q - кількість товару (у шт.),
P - ціна одиниці товару)
Знайти:
CS (споживчий надлишок)
Задача
Попит
Ринкова рівновага
P*
Q*
= 1
PD = 4 - Q2
Споживчий надлишок - ?
Дано:
PD = 4 - Q2
P* = Q* = 1
(Q - кількість товару (у шт.),
P - ціна одиниці товару)
Знайти:
CS (споживчий надлишок)
Задача
Попит
Ринкова рівновага
P*
Q*
= 1
PD = 4 - Q2
Споживчий надлишок - ?
Слайд #14
За виведеною формулою визначення споживчого надлишку маємо:
Розв'язання
Отже, за даний товар споживачі готові заплатити на грн. більше за реальні витрати на його придбання.
Відповідь: CS = грн.
Розв'язання
Отже, за даний товар споживачі готові заплатити на грн. більше за реальні витрати на його придбання.
Відповідь: CS = грн.

Слайд #15
Дякую за увагу!
