- Головна
- Готові шкільні презентації
- Презентація на тему «Начальные сведения по стереометрии»
Презентація на тему «Начальные сведения по стереометрии»
269
Слайд #1
Начальные сведения по стереометрии.
Плоскости в пространстве.
Плоскости в пространстве.

Слайд #2
Стереометрия. Примеры пространственных фигур.
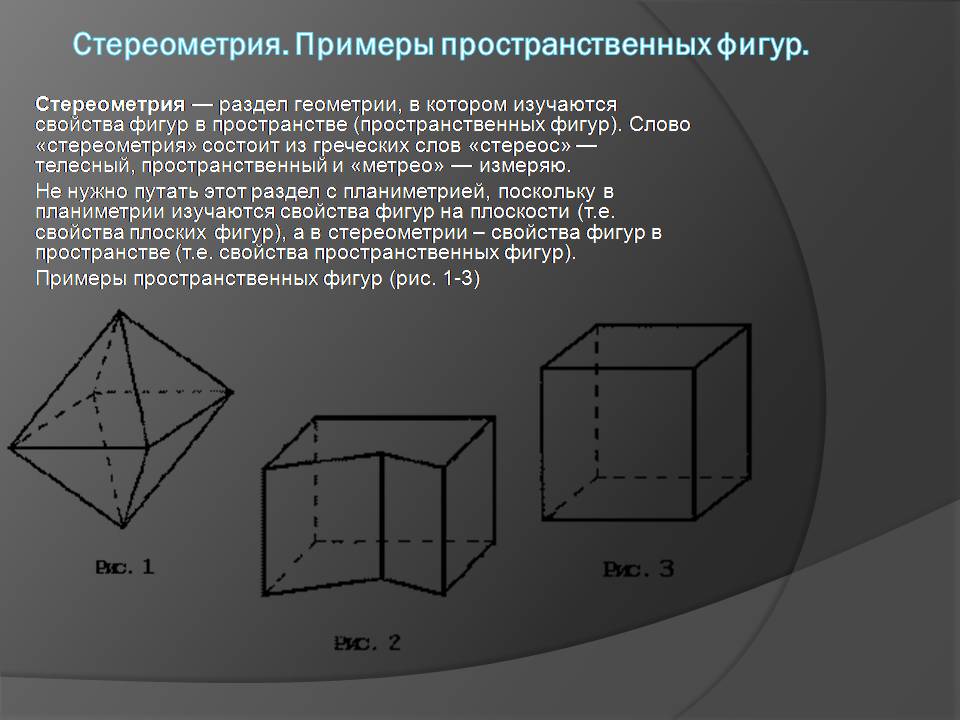
Стереометрия — раздел геометрии, в котором изучаются свойства фигур в пространстве (пространственных фигур). Слово «стереометрия» состоит из греческих слов «стереос» — телесный, пространственный и «метрео» — измеряю.
Не нужно путать этот раздел с планиметрией, поскольку в планиметрии изучаются свойства фигур на плоскости (т.е. свойства плоских фигур), а в стереометрии – свойства фигур в пространстве (т.е. свойства пространственных фигур).
Примеры пространственных фигур (рис. 1-3)
Стереометрия — раздел геометрии, в котором изучаются свойства фигур в пространстве (пространственных фигур). Слово «стереометрия» состоит из греческих слов «стереос» — телесный, пространственный и «метрео» — измеряю.
Не нужно путать этот раздел с планиметрией, поскольку в планиметрии изучаются свойства фигур на плоскости (т.е. свойства плоских фигур), а в стереометрии – свойства фигур в пространстве (т.е. свойства пространственных фигур).
Примеры пространственных фигур (рис. 1-3)
Слайд #3
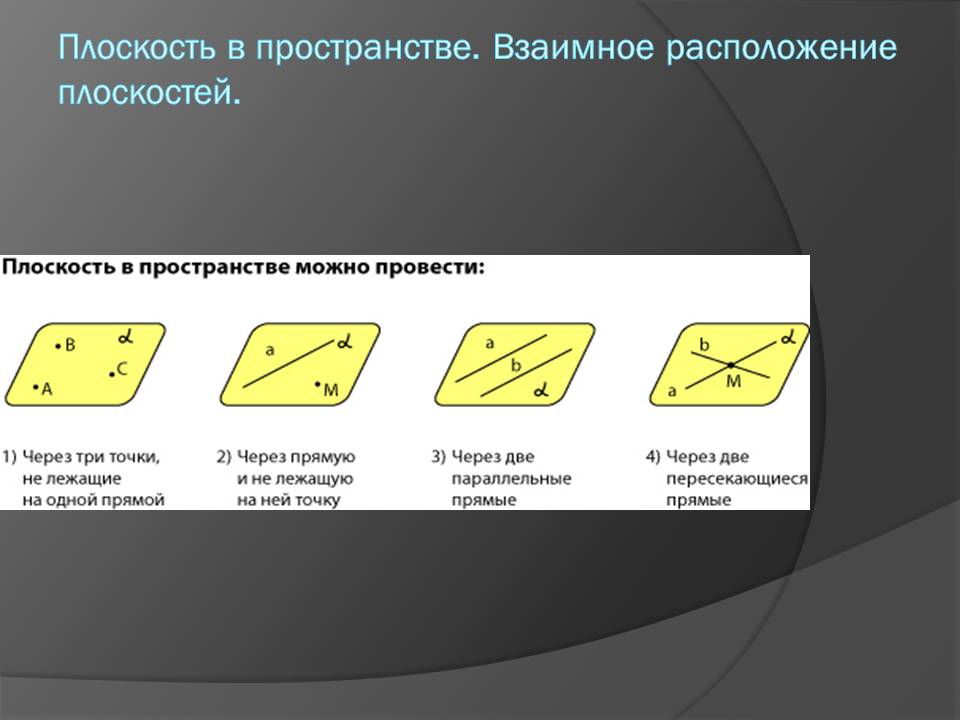
Плоскость в пространстве. Взаимное расположение плоскостей.
Плоскость, прямая, точка — основные понятия геометрии. Нам трудно
дать им четкие определения, однако интуитивно мы понимаем, что это
такое. Плоскость имеет только два измерения. У нее нет глубины.
Прямая имеет лишь одно измерение, а у точки вообще нет размеров —
ни длины, ни ширины, ни высоты.
Плоскость бесконечна. Поэтому в задачах мы рисуем только часть
плоскости.
Плоскость, прямая, точка — основные понятия геометрии. Нам трудно
дать им четкие определения, однако интуитивно мы понимаем, что это
такое. Плоскость имеет только два измерения. У нее нет глубины.
Прямая имеет лишь одно измерение, а у точки вообще нет размеров —
ни длины, ни ширины, ни высоты.
Плоскость бесконечна. Поэтому в задачах мы рисуем только часть
плоскости.

Слайд #4
Плоскость в пространстве. Взаимное расположение плоскостей.
Слайд #5
Плоскость в пространстве. Взаимное расположение плоскостей.
А как предыдущие утверждения выглядят в пространстве?
Очень просто. Лист плотной бумаги послужит «моделью»
плоскости. Можно взять и другой плоский предмет, например, CD-диск, пластиковую карту. Карандаши вполне могут изобразить прямые. Все аксиомы и теоремы стереометрии можно показать «на пальцах», то есть с помощью подручных материалов.
А как предыдущие утверждения выглядят в пространстве?
Очень просто. Лист плотной бумаги послужит «моделью»
плоскости. Можно взять и другой плоский предмет, например, CD-диск, пластиковую карту. Карандаши вполне могут изобразить прямые. Все аксиомы и теоремы стереометрии можно показать «на пальцах», то есть с помощью подручных материалов.

Слайд #6
Плоскость в пространстве. Взаимное расположение плоскостей.
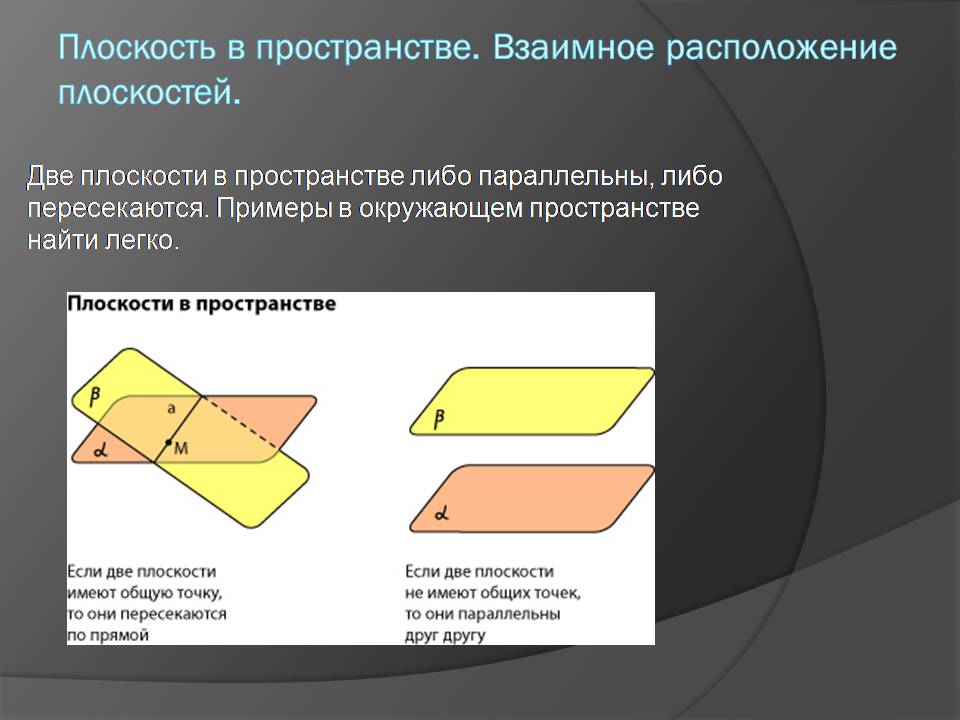
Две плоскости в пространстве либо параллельны, либо пересекаются. Примеры в окружающем пространстве найти легко.
Две плоскости в пространстве либо параллельны, либо пересекаются. Примеры в окружающем пространстве найти легко.
Слайд #7
Прямая призма. Пирамида.
Многогранником называется такое тело, поверхность которого состоит из конечного числа плоских многоугольников.
Прямая призма относится к простейшим многогранникам. Каждая грань (многоугольник, ограничивающий многогранник) многогранника расположена в своей плоскости. Пересечение граней многогранника проходит по линии его ребер.
На рис. 18 — пятигранная прямоугольная призма (в основании призмы лежит пятиугольник). У нее 10 вершин; 5 боковых граней; 2 основания (верхнее и нижнее). Для прямоугольной призмы высотой служит любое ребро, расположенное перпендикулярно основанию.
Многогранником называется такое тело, поверхность которого состоит из конечного числа плоских многоугольников.
Прямая призма относится к простейшим многогранникам. Каждая грань (многоугольник, ограничивающий многогранник) многогранника расположена в своей плоскости. Пересечение граней многогранника проходит по линии его ребер.
На рис. 18 — пятигранная прямоугольная призма (в основании призмы лежит пятиугольник). У нее 10 вершин; 5 боковых граней; 2 основания (верхнее и нижнее). Для прямоугольной призмы высотой служит любое ребро, расположенное перпендикулярно основанию.

Слайд #8
Призма — это многогранник, у которого две грани, называемые основаниями, — равные многоугольники, а все остальные — боковые грани, состоящие из параллелограммов, плоскости которых параллельны одной прямой, называемой ребром многогранника.
Высота призмы — это расстояние между ее основаниями. Для прямой призмы, у которой все ребра перпендикулярны основаниям, — это любое из ребер.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю призмы.
Площадь боковой поверхности призмы равна произведению периметра основания и высоты.
Sбок = p * h
Объем прямой призмы равен произведению площади основания и длины бокового ребра.
V = Sбок * l
Высота призмы — это расстояние между ее основаниями. Для прямой призмы, у которой все ребра перпендикулярны основаниям, — это любое из ребер.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю призмы.
Площадь боковой поверхности призмы равна произведению периметра основания и высоты.
Sбок = p * h
Объем прямой призмы равен произведению площади основания и длины бокового ребра.
V = Sбок * l

Слайд #9
Пирами́да — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д.Пирамида является частным случаем конуса.

Слайд #10
Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды:
Площадь полной поверхности пирамидыПлощадью поверхности пирамиды называется сумма площадей всех ее граней .
Площадь боковой поверхности — сумма площадей всех боковых граней .
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды:
Площадь полной поверхности пирамидыПлощадью поверхности пирамиды называется сумма площадей всех ее граней .
Площадь боковой поверхности — сумма площадей всех боковых граней .

Слайд #11
Конус. Цилиндр. Шар.
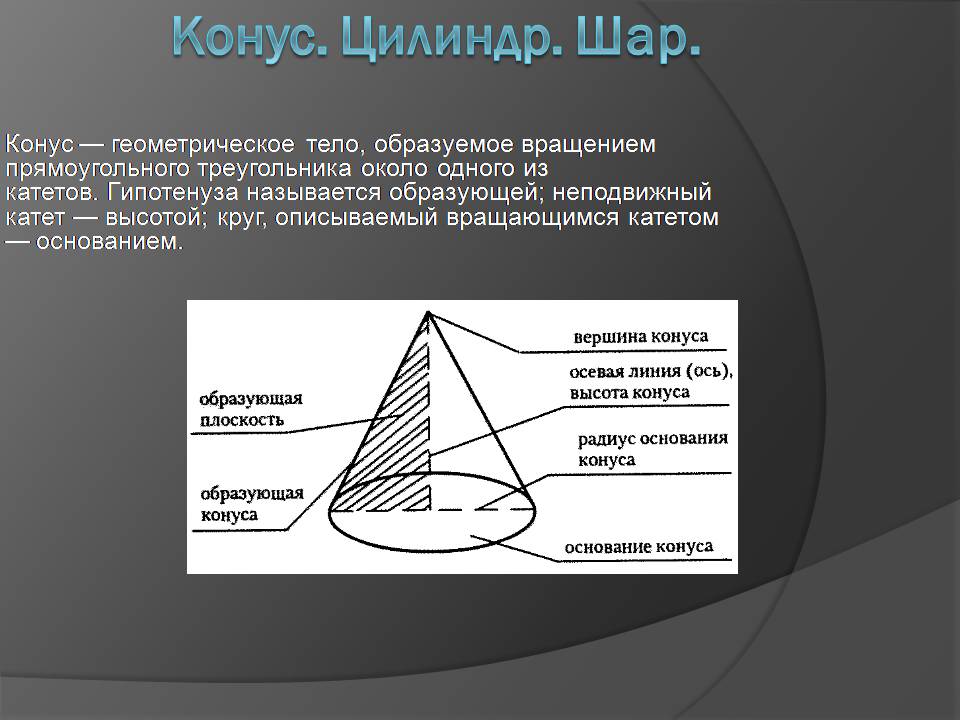
Конус — геометрическое тело, образуемое вращением прямоугольного треугольника около одного из катетов. Гипотенуза называется образующей; неподвижный катет — высотой; круг, описываемый вращающимся катетом — основанием.
Конус — геометрическое тело, образуемое вращением прямоугольного треугольника около одного из катетов. Гипотенуза называется образующей; неподвижный катет — высотой; круг, описываемый вращающимся катетом — основанием.
Слайд #12
Боковая поверхность конуса равна произведению окружности основания на половину образующей.
Объем конуса равен площади основания, умноженной на треть высоты.
Объем конуса равен площади основания, умноженной на треть высоты.

Слайд #13
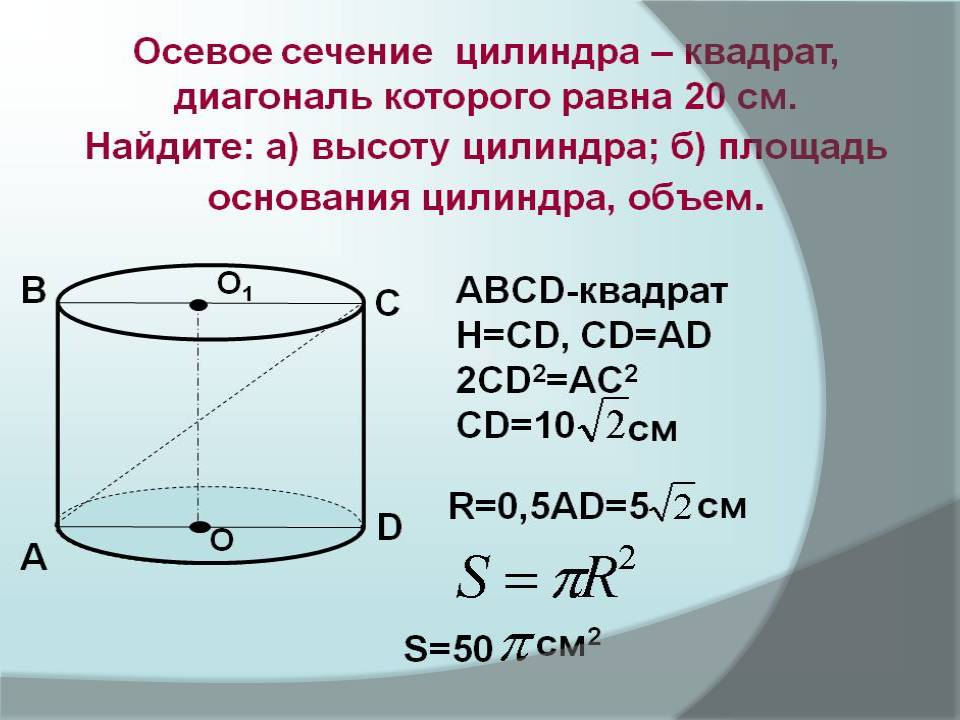
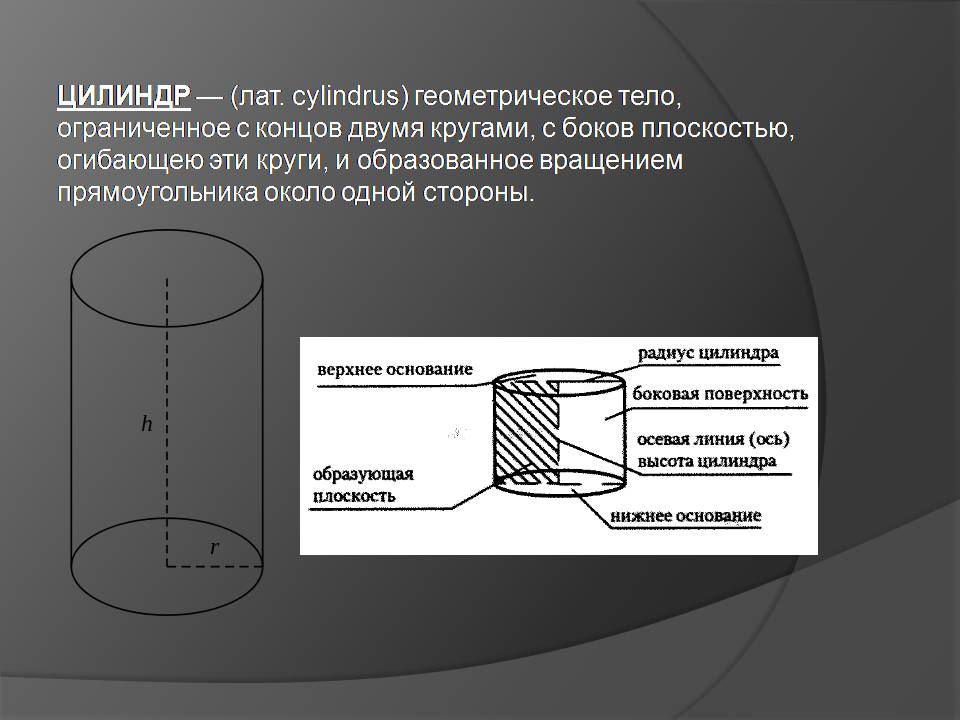
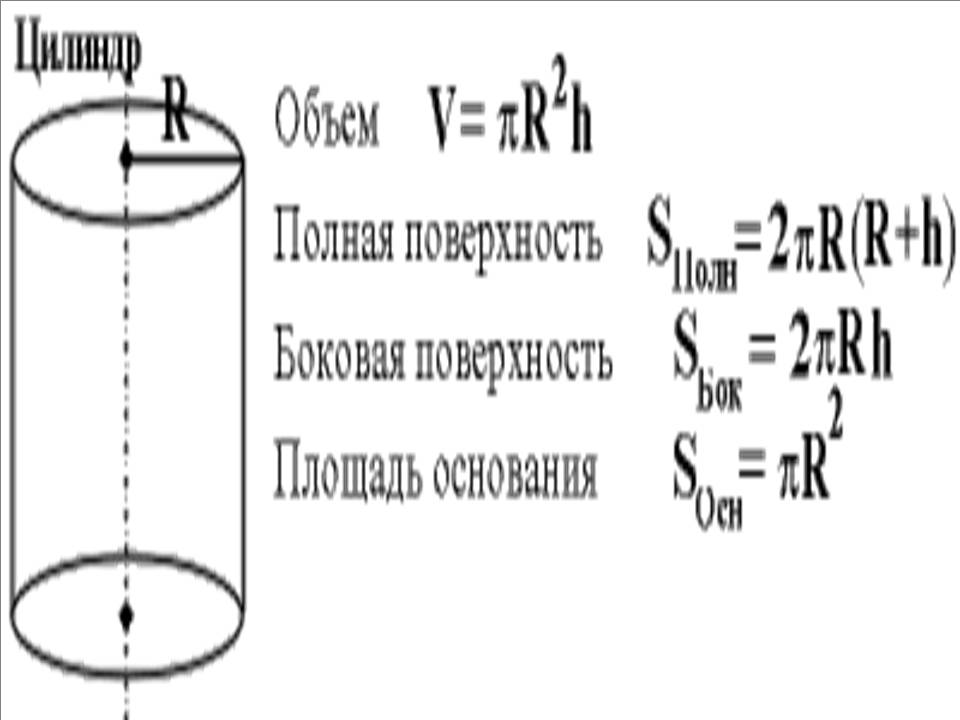
ЦИЛИНДР — (лат. cylindrus) геометрическое тело, ограниченное с концов двумя кругами, с боков плоскостью, огибающею эти круги, и образованное вращением прямоугольника около одной стороны.
Слайд #14
ЦИЛИНДР — (лат. cylindrus) геометрическое тело, ограниченное с концов двумя кругами, с боков плоскостью, огибающею эти круги, и образованное вращением прямоугольника около одной стороны.
Слайд #15
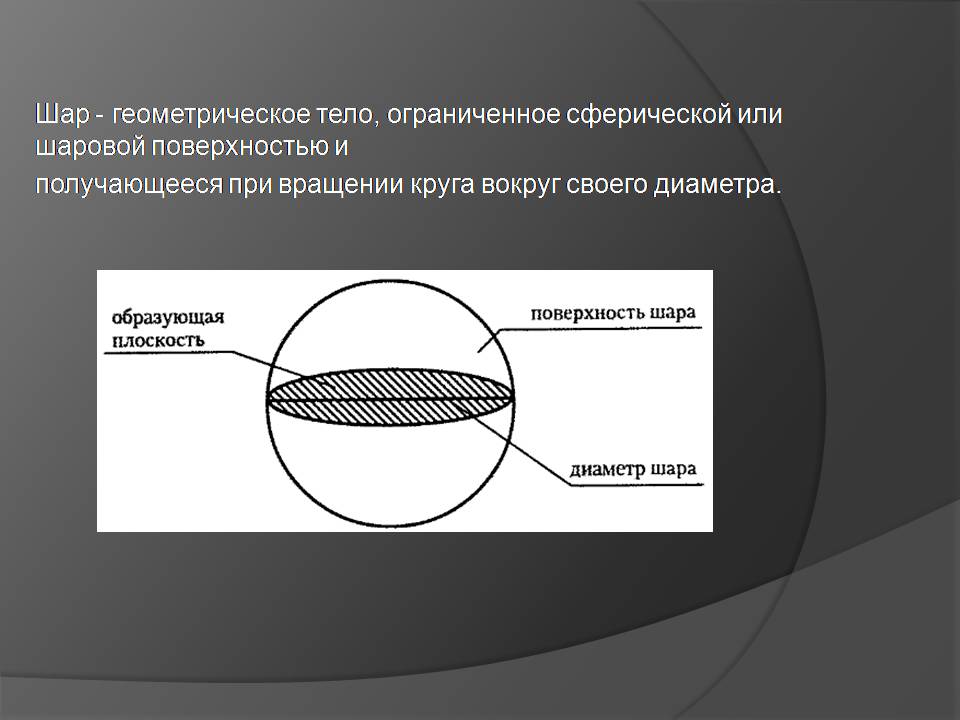
Шар - геометрическое тело, ограниченное сферической или шаровой поверхностью и
получающееся при вращении круга вокруг своего диаметра.
получающееся при вращении круга вокруг своего диаметра.
Слайд #16
Площадь и объем шара.

Слайд #17
Площадь и объем шара.
Слайд #18
Площадь и объем шара.

Слайд #19