- Головна
- Готові шкільні презентації
- Презентація на тему «Функція у = х^2»
Презентація на тему «Функція у = х^2»
269
Слайд #1
Функція у = х2

Слайд #2
Ніякої достоверності нема в науках там, де не можна застосовувати хоча б одну з математичних наук , і в тому, що не має зв'язку з математикою. Леонардо да Вінчі
13.03.2015
2
13.03.2015
2

Слайд #3
формувати навики роботи з графіком функції
формувати вміння відтворювати зміст
вивчених понять
застосовувати графік функції у = х2 для
графічного розв'язання рівнянь
вміти будувати графік функції у = х2
засвоїти властивості функції у = х2
Мета уроку:
формувати вміння відтворювати зміст
вивчених понять
застосовувати графік функції у = х2 для
графічного розв'язання рівнянь
вміти будувати графік функції у = х2
засвоїти властивості функції у = х2
Мета уроку:

Слайд #4
Пригадаймо :
Сформулюйте означення функції.
Що таке область визначення функції ?
Що таке область значень функції ?
Що таке аргумент функції ?
Як можна задавати функцію ?
Що таке графік функції ?
Яка функція називається зростаючою ?
Яка функція називається спадною ?
Сформулюйте означення функції.
Що таке область визначення функції ?
Що таке область значень функції ?
Що таке аргумент функції ?
Як можна задавати функцію ?
Що таке графік функції ?
Яка функція називається зростаючою ?
Яка функція називається спадною ?

Слайд #5
Функція у = х2
графіком є парабола
(0;0) – вершина параболи
вісь у – вісь симетрії
функція спадає при х < 0
функція зростає при х > 0
функція у = х2 –
найпростіша із
квадратичних функцій
графіком є парабола
(0;0) – вершина параболи
вісь у – вісь симетрії
функція спадає при х < 0
функція зростає при х > 0
функція у = х2 –
найпростіша із
квадратичних функцій
Слайд #6
Розв'яжіть графічним способом рівняння :
Розв'язання :
Побудуємо в одній системі
координат графіки функцій
та
Ці графіки перетинаються в точках , абсциси яких дорівнюють -2 і 2. Отже, дане рівняння має два корені х=-2 і х=2.
Відповідь: -2; 2.
6
Розв'язання :
Побудуємо в одній системі
координат графіки функцій
та
Ці графіки перетинаються в точках , абсциси яких дорівнюють -2 і 2. Отже, дане рівняння має два корені х=-2 і х=2.
Відповідь: -2; 2.
6

Слайд #7
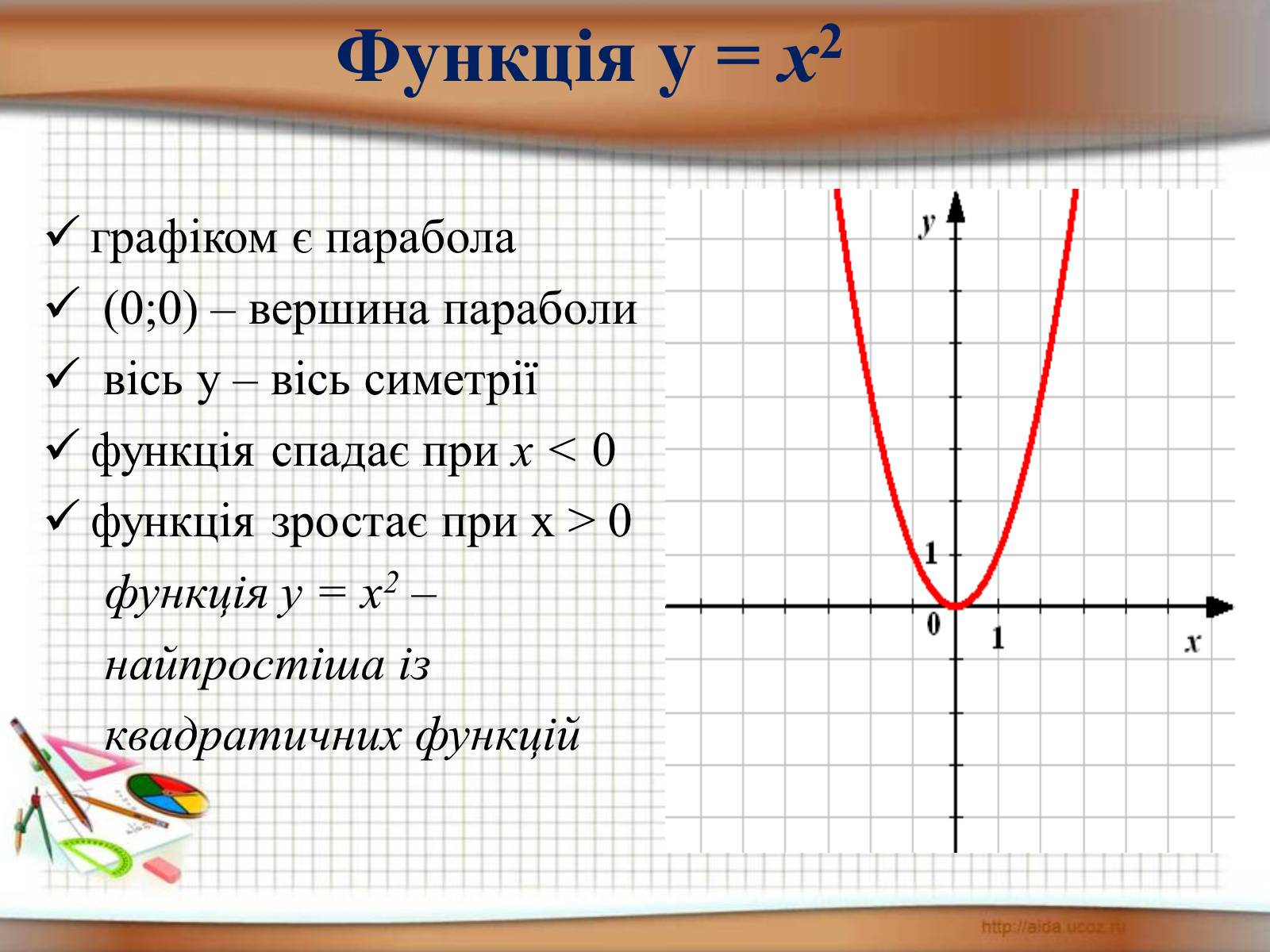
Розв'яжіть графічним способом рівняння :
Розв'язання :
Побудуємо в одній системі
координат графіки функцій
та
Ці графіки перетинаються в точках , абсциси яких дорівнюють -1,3 і 2,2 (можливо, наближено). Отже, дане рівняння має два корені х=-1,3 і х=2,2. Відповідь: -2; 2.
Розв'язання :
Побудуємо в одній системі
координат графіки функцій
та
Ці графіки перетинаються в точках , абсциси яких дорівнюють -1,3 і 2,2 (можливо, наближено). Отже, дане рівняння має два корені х=-1,3 і х=2,2. Відповідь: -2; 2.
Слайд #8
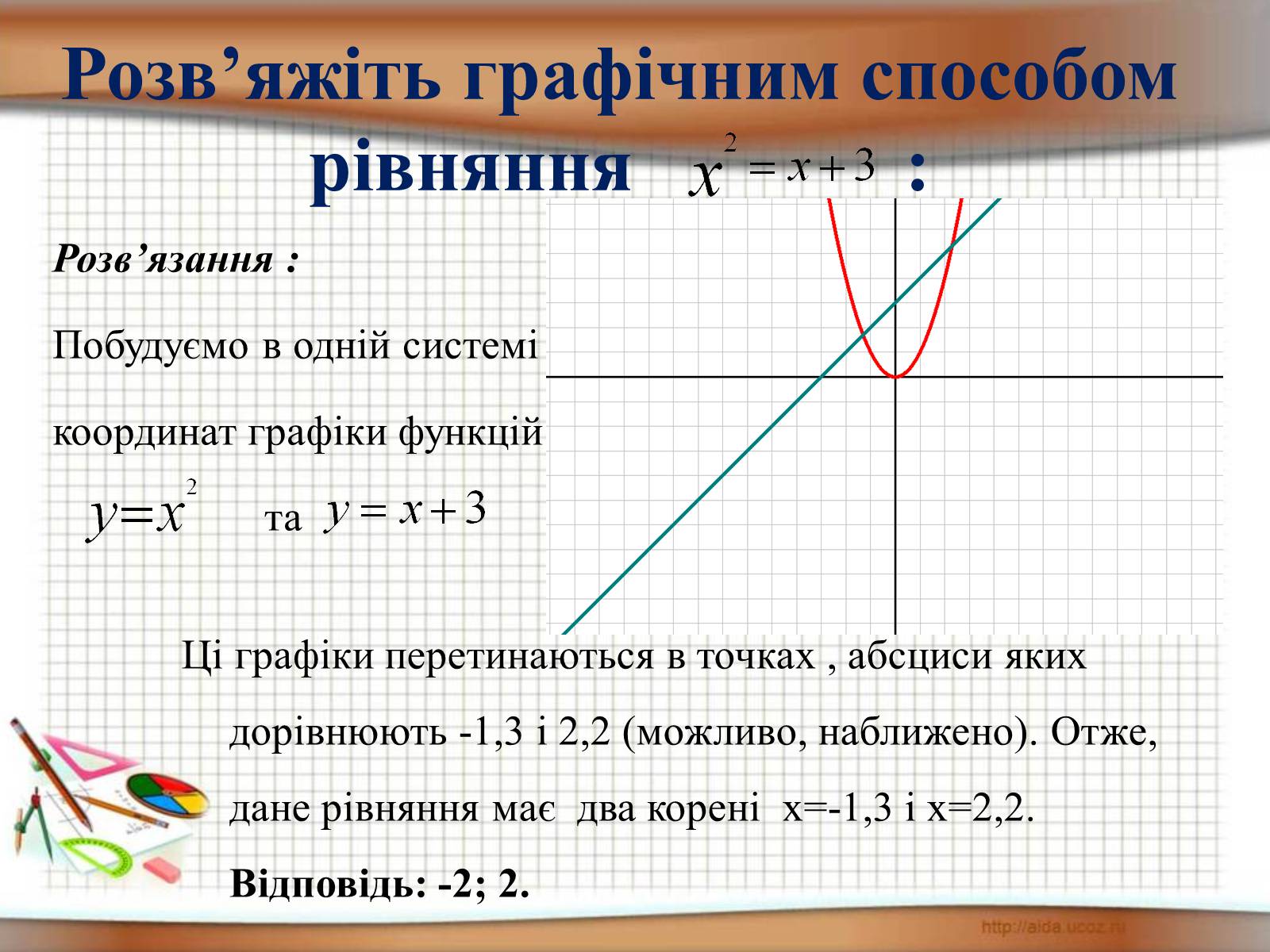
Розв'яжіть графічним способом рівняння :
Розв'язання :
Побудуємо в одній
Системі координат
графіки функцій
та
Ці графіки не перетинаються . Отже, дане рівняння не має коренів. Відповідь: коренів не має.
Розв'язання :
Побудуємо в одній
Системі координат
графіки функцій
та
Ці графіки не перетинаються . Отже, дане рівняння не має коренів. Відповідь: коренів не має.
Слайд #9
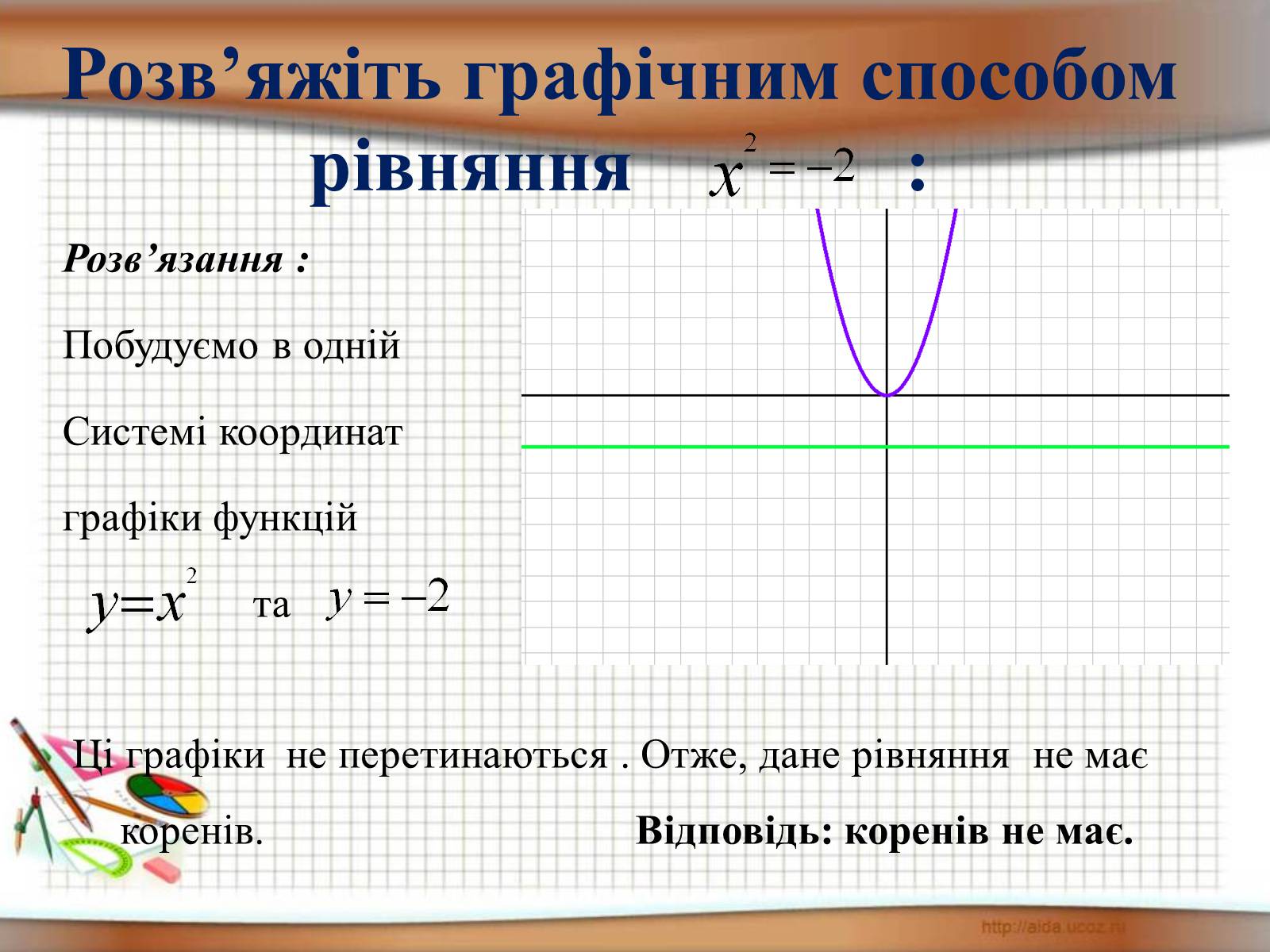
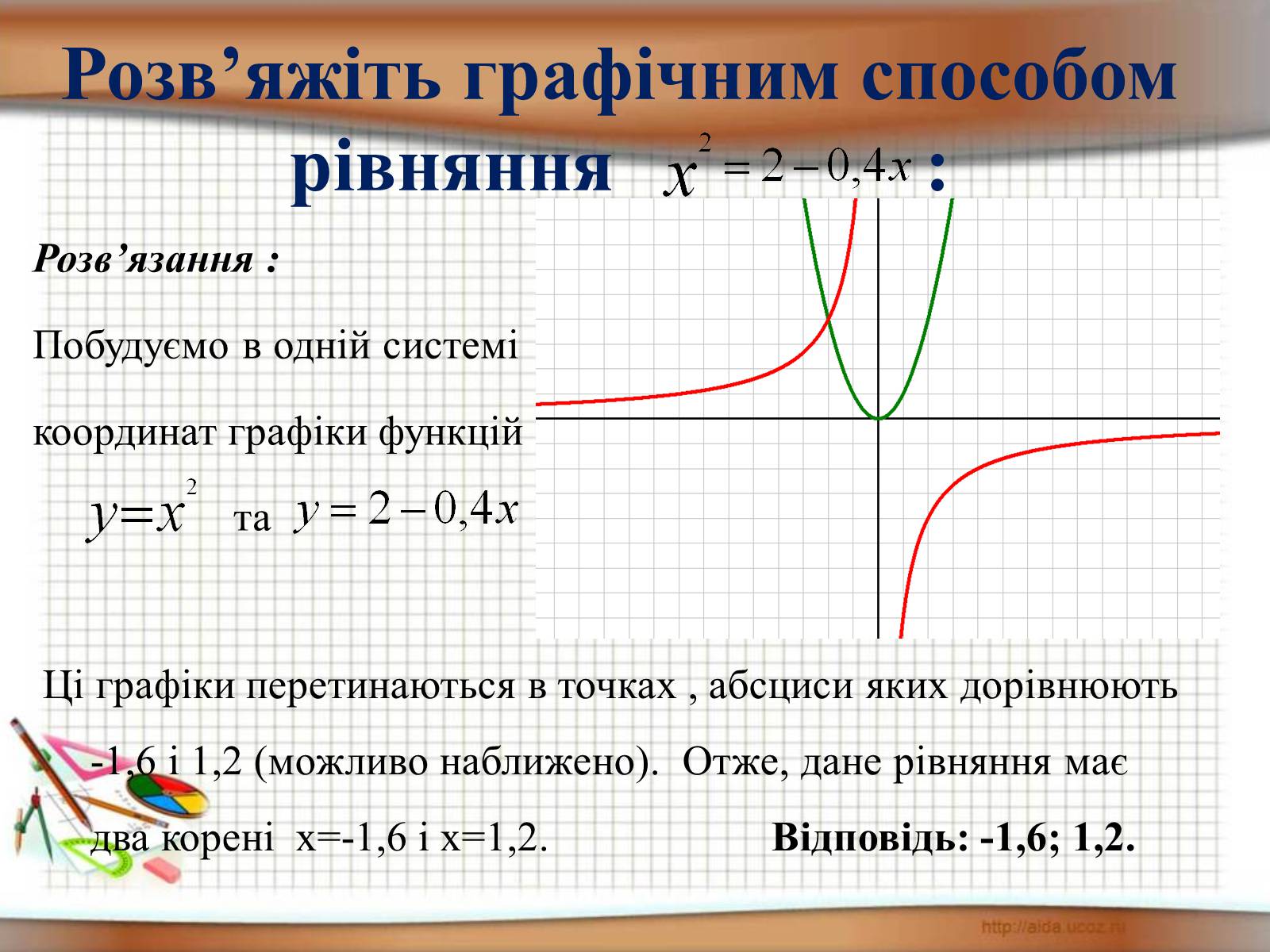
Розв'яжіть графічним способом рівняння :
Розв'язання :
Побудуємо в одній системі
координат графіки функцій
та
Ці графіки перетинаються в точках , абсциси яких дорівнюють -1,6 і 1,2 (можливо наближено). Отже, дане рівняння має два корені х=-1,6 і х=1,2. Відповідь: -1,6; 1,2.
Розв'язання :
Побудуємо в одній системі
координат графіки функцій
та
Ці графіки перетинаються в точках , абсциси яких дорівнюють -1,6 і 1,2 (можливо наближено). Отже, дане рівняння має два корені х=-1,6 і х=1,2. Відповідь: -1,6; 1,2.
Слайд #10
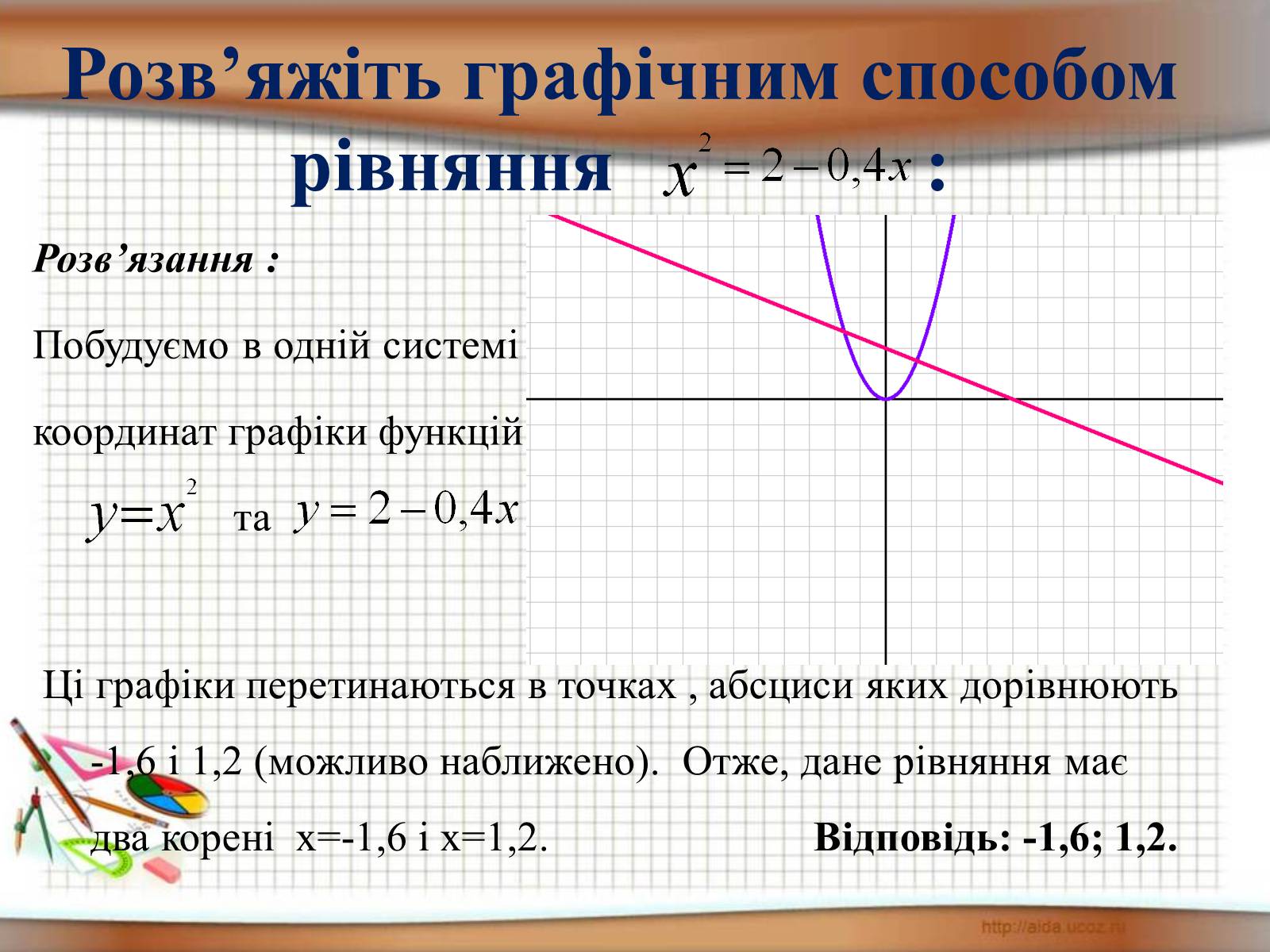
Розв'яжіть графічним способом рівняння :
Розв'язання :
Побудуємо в одній системі
координат графіки функцій
та
Ці графіки перетинаються в точці , абсциса якої дорівнює 1.
Отже, дане рівняння має корінь х=1.
Відповідь: 1.
Розв'язання :
Побудуємо в одній системі
координат графіки функцій
та
Ці графіки перетинаються в точці , абсциса якої дорівнює 1.
Отже, дане рівняння має корінь х=1.
Відповідь: 1.

Слайд #11
Розв'яжіть графічним способом рівняння :
Розв'язання :
Побудуємо в одній системі
координат графіки функцій
та
Ці графіки перетинаються в точках , абсциси яких дорівнюють -1,6 і 1,2 (можливо наближено). Отже, дане рівняння має два корені х=-1,6 і х=1,2. Відповідь: -1,6; 1,2.
Розв'язання :
Побудуємо в одній системі
координат графіки функцій
та
Ці графіки перетинаються в точках , абсциси яких дорівнюють -1,6 і 1,2 (можливо наближено). Отже, дане рівняння має два корені х=-1,6 і х=1,2. Відповідь: -1,6; 1,2.
Слайд #12
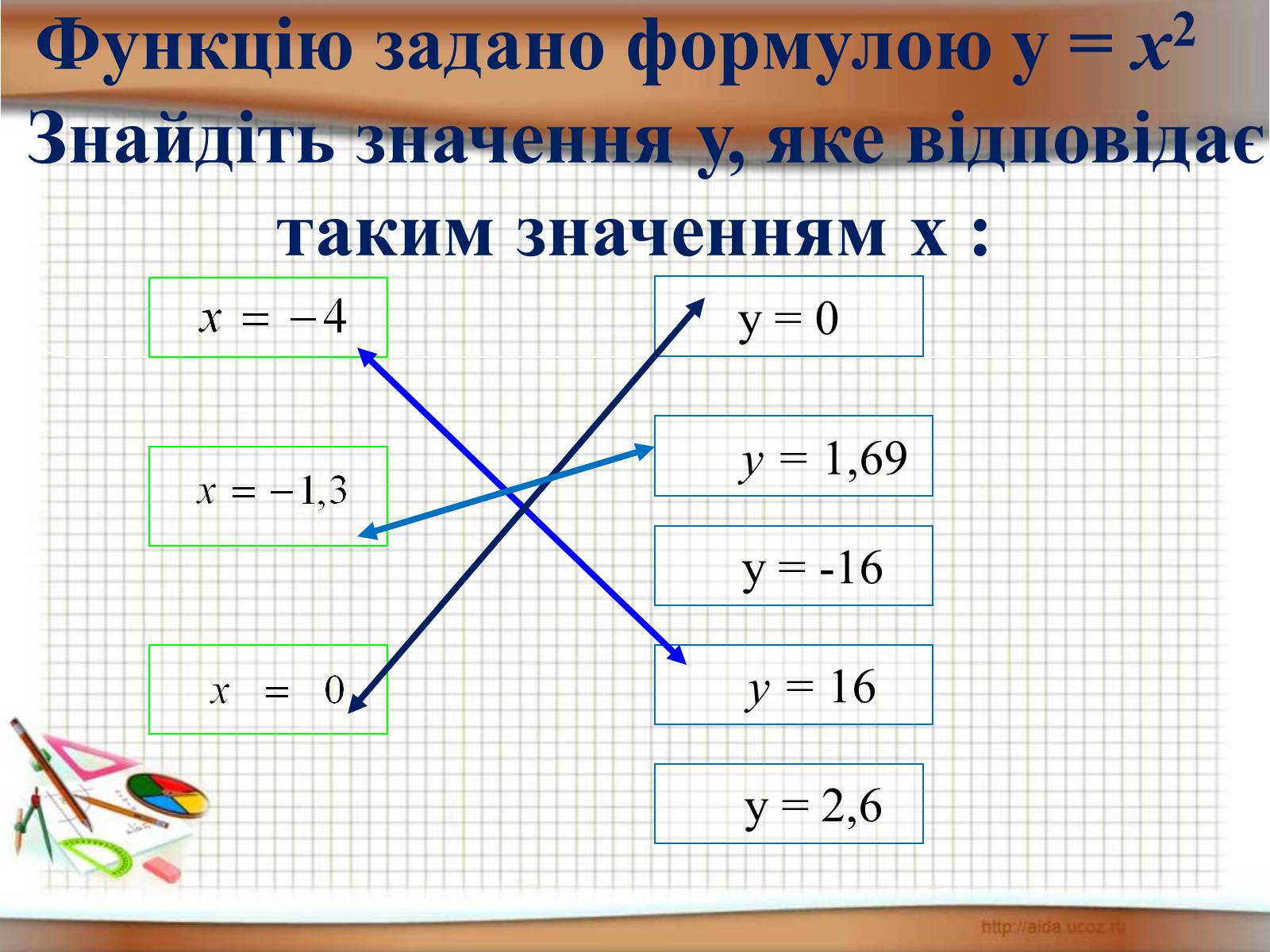
Функцію задано формулою у = х2
Знайдіть значення у, яке відповідає
таким значенням х :
y = 0
у = 1,69
y = -16
y = 2,6
y = 16
Знайдіть значення у, яке відповідає
таким значенням х :
y = 0
у = 1,69
y = -16
y = 2,6
y = 16
Слайд #13
х = 0,2; х=-0,2
х=11; х=-11
х=7
х=11
х=-7 ; х=7
Функцію задано формулою у = х2 Знайдіть значення х, яким відповідають такі значення у :
х=11; х=-11
х=7
х=11
х=-7 ; х=7
Функцію задано формулою у = х2 Знайдіть значення х, яким відповідають такі значення у :

Слайд #14
1,5
5,2
-0,5
4
0,5
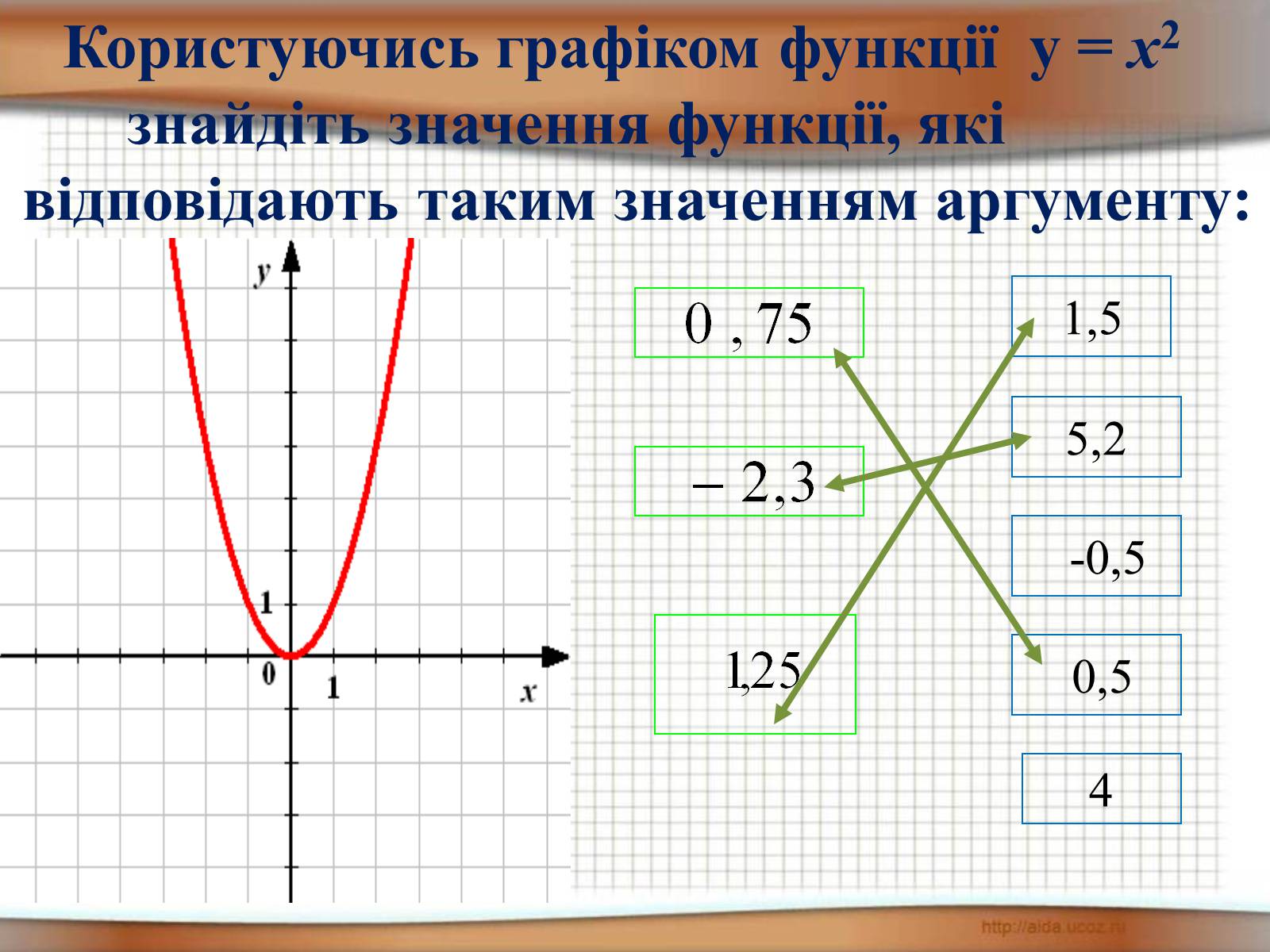
Користуючись графіком функції у = х2
знайдіть значення функції, які
відповідають таким значенням аргументу:
5,2
-0,5
4
0,5
Користуючись графіком функції у = х2
знайдіть значення функції, які
відповідають таким значенням аргументу:
Слайд #15
Графіком якої з наведених функцій є парабола з вершиною в точці О(0;0) :
Відповідь: В
А) у = х – 3 ;
Б) у = ;
В) у = х2 ;
Г) у = | х | + 2 ?
Відповідь: В
А) у = х – 3 ;
Б) у = ;
В) у = х2 ;
Г) у = | х | + 2 ?

Слайд #16
Вкажіть правильне твердження:
Відповідь: Г)
А) областю значень функції у = х2 є множина всіх
дійсних чисел;
Б) функція у = х2 може набувати від'ємних значень ;
В) графіком функції у = х2 є гіпербола ;
Г) графік функції у = х2 симетричний відносно осі у.
Відповідь: Г)
А) областю значень функції у = х2 є множина всіх
дійсних чисел;
Б) функція у = х2 може набувати від'ємних значень ;
В) графіком функції у = х2 є гіпербола ;
Г) графік функції у = х2 симетричний відносно осі у.

Слайд #17
Через яку точку проходить графік функції у = х2
Відповідь: Б)
А) М ( -7; -49),
Б) Р ( 3; 9 ),
В) С ( 0,2 ; 0,4),
Г) В ( 25; 5) ?
Відповідь: Б)
А) М ( -7; -49),
Б) Р ( 3; 9 ),
В) С ( 0,2 ; 0,4),
Г) В ( 25; 5) ?

Слайд #18
Яка із систем має два розв'язки ?
Відповідь: Б
Відповідь: Б

Слайд #19
Графік якої функції не перетинає графік функції у = х2
Відповідь: Г
А) у = 3,
Б) у = 9,
В) у = 0,
Г) у = -2 ?
Відповідь: Г
А) у = 3,
Б) у = 9,
В) у = 0,
Г) у = -2 ?

Слайд #20
Підсумок уроку:“незакінченні речення “
Лінію, що є графіком функції у = х2 , називають …
О(0;0) - … параболи.
Функція у = х2 спадає, якщо х -…
Функція у = х2 зростає, якщо х –…
Областю визначення функції у = х2 є …
Областю значень функції у = х2 є …
Графік функції у = х2 розташований у … координатних чвертях.
Лінію, що є графіком функції у = х2 , називають …
О(0;0) - … параболи.
Функція у = х2 спадає, якщо х -…
Функція у = х2 зростає, якщо х –…
Областю визначення функції у = х2 є …
Областю значень функції у = х2 є …
Графік функції у = х2 розташований у … координатних чвертях.

Слайд #21
Цікаві факти
На фронтах Великої Вітчизняної війни були
застосовані артилерійські снаряди, які називалися
“підкаліберними”. Сила такого бронебойного
снаряда визначається кінетичною енергією .
Інженери, урахувавши цю властивість, зробили
пристрої, що надавали снаряду більшої швидкості і пропорційно її квадрату зростала бронебойна сила снаряда.
На фронтах Великої Вітчизняної війни були
застосовані артилерійські снаряди, які називалися
“підкаліберними”. Сила такого бронебойного
снаряда визначається кінетичною енергією .
Інженери, урахувавши цю властивість, зробили
пристрої, що надавали снаряду більшої швидкості і пропорційно її квадрату зростала бронебойна сила снаряда.

Слайд #22
Рефлексія
Що нового ви дізналися на сьогоднішньому уроці?
Чи досягли поставленої мети ?
Що на уроці було головне ?
Чим поповнили свої знання ?
Що нового ви дізналися на сьогоднішньому уроці?
Чи досягли поставленої мети ?
Що на уроці було головне ?
Чим поповнили свої знання ?

Слайд #23
Домашнє завдання
Опрацювати п.13 (ст.127) .
Рівень А: №№ 583, 585, 589 (с.131) ;
Рівень Б : №№ 592, 595, 600 (с.131).
Опрацювати п.13 (ст.127) .
Рівень А: №№ 583, 585, 589 (с.131) ;
Рівень Б : №№ 592, 595, 600 (с.131).
