- Головна
- Готові шкільні презентації
- Презентація на тему «Формула коренів»
Презентація на тему «Формула коренів»
479
Слайд #1
Формула коренів
квадратного рівняння
квадратного рівняння

Слайд #2
Що таке квадратне рівняння?
Квадратним рівнянням називають рівняння виду
ax2+bx+c=0,
де x – змінна, a, b, c – деякі числа, причому a∉0 .
a, b, c – коефіцієнти квадратного рівняння
a – перший (старший) коефіцієнт;
b – другий коефіцієнт;
с – вільний член.
Квадратним рівнянням називають рівняння виду
ax2+bx+c=0,
де x – змінна, a, b, c – деякі числа, причому a∉0 .
a, b, c – коефіцієнти квадратного рівняння
a – перший (старший) коефіцієнт;
b – другий коефіцієнт;
с – вільний член.

Слайд #3
Що таке квадратне рівняння?
Квадратним рівнянням називають рівняння виду
ax2+bx+c=0,
де x – змінна, a, b, c – деякі числа, причому a∉0 .
a, b, c – коефіцієнти квадратного рівняння
a – перший (старший) коефіцієнт;
b – другий коефіцієнт;
с – вільний член.
Квадратним рівнянням називають рівняння виду
ax2+bx+c=0,
де x – змінна, a, b, c – деякі числа, причому a∉0 .
a, b, c – коефіцієнти квадратного рівняння
a – перший (старший) коефіцієнт;
b – другий коефіцієнт;
с – вільний член.
Слайд #4
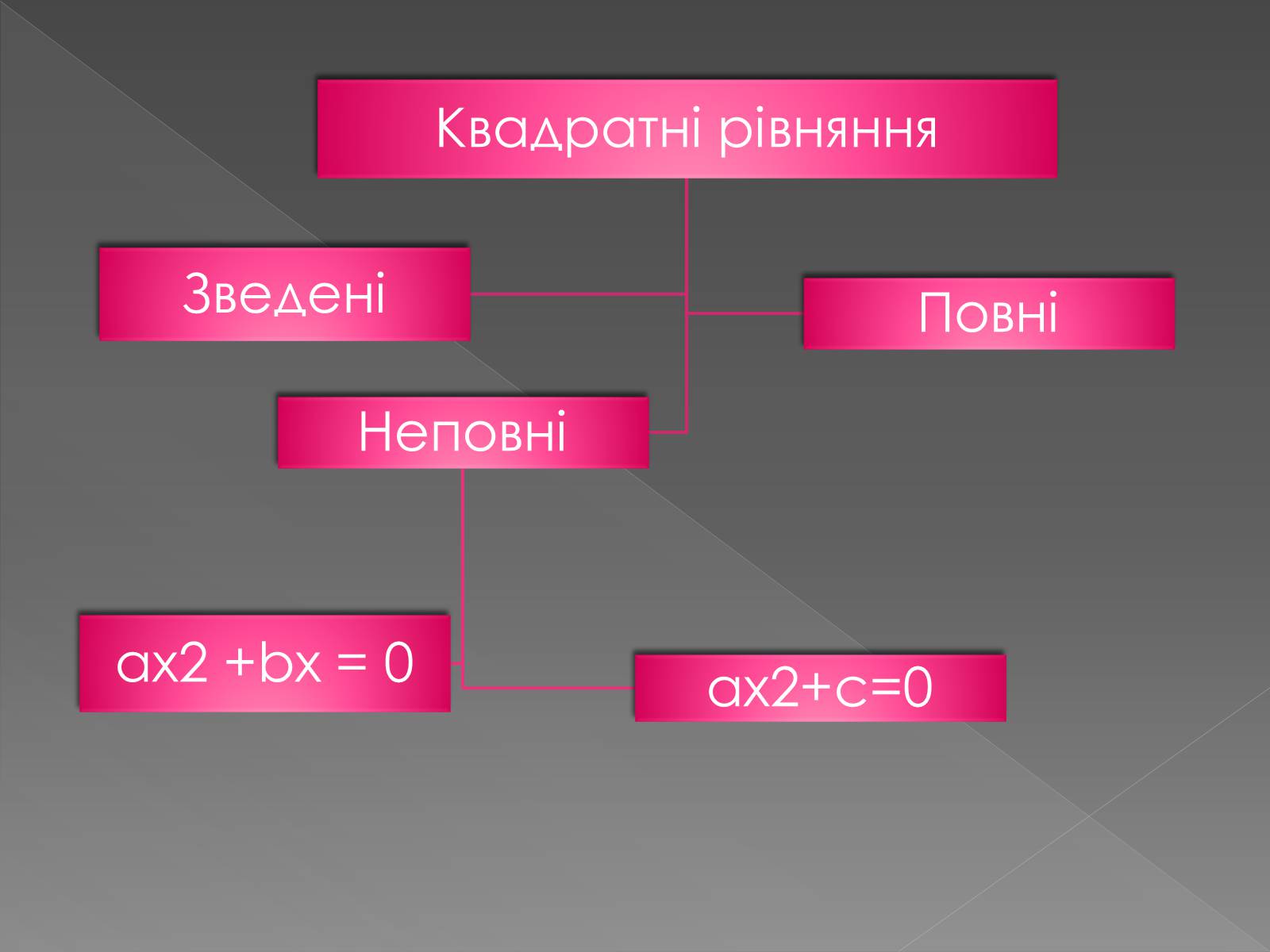
Що таке неповні рівняння?
Неповним квадратним рівнянням, називають рівняння в якому хоча б один коефіцієнт дорівнює 0.
Неповним квадратним рівнянням, називають рівняння в якому хоча б один коефіцієнт дорівнює 0.

Слайд #5
Коли в рівнянні b=0 рівняння має такий вигляд: ax2+c=0
Це рівняння розв'язується так: змінну залишаємо в лівій частині, число переносимо в праву.Наприклад: 2х2-8=0
2х2=8
х2=4
х= +-2
Це рівняння розв'язується так: змінну залишаємо в лівій частині, число переносимо в праву.Наприклад: 2х2-8=0
2х2=8
х2=4
х= +-2

Слайд #6
Якщо в рівнянні с=0, воно має такий вигляд: ax2 +bx = 0.Воно розв'язується так: х виносимо за дужки і прирівнюємо до нуля кожен з множників.
Наприклад: 3х2-6х=0
х(3х-6)=0
х=0 або 3х-6=0
3х=6
х=2
Наприклад: 3х2-6х=0
х(3х-6)=0
х=0 або 3х-6=0
3х=6
х=2

Слайд #7
Рівняння виду х2+bx+с = 0, у якому а=0, називається зведеним.Зведене рівняння розв'язується за теоремою Вієта, в якій х1*х2=с
х1+х2=b
Наприклад: х2-5х+6= 0
х1*х2=6 х1=2 х1+х2=5 х2=3
х1+х2=b
Наприклад: х2-5х+6= 0
х1*х2=6 х1=2 х1+х2=5 х2=3

Слайд #8
Рівняння виду ах2+bx+с=0, називають повним.
Повне рівняння може розв'язуватись двома способами:
- за дискримінантом
-за теоремою Вієта для
повного квадратного
рівняння;
Повне рівняння може розв'язуватись двома способами:
- за дискримінантом
-за теоремою Вієта для
повного квадратного
рівняння;

Слайд #9
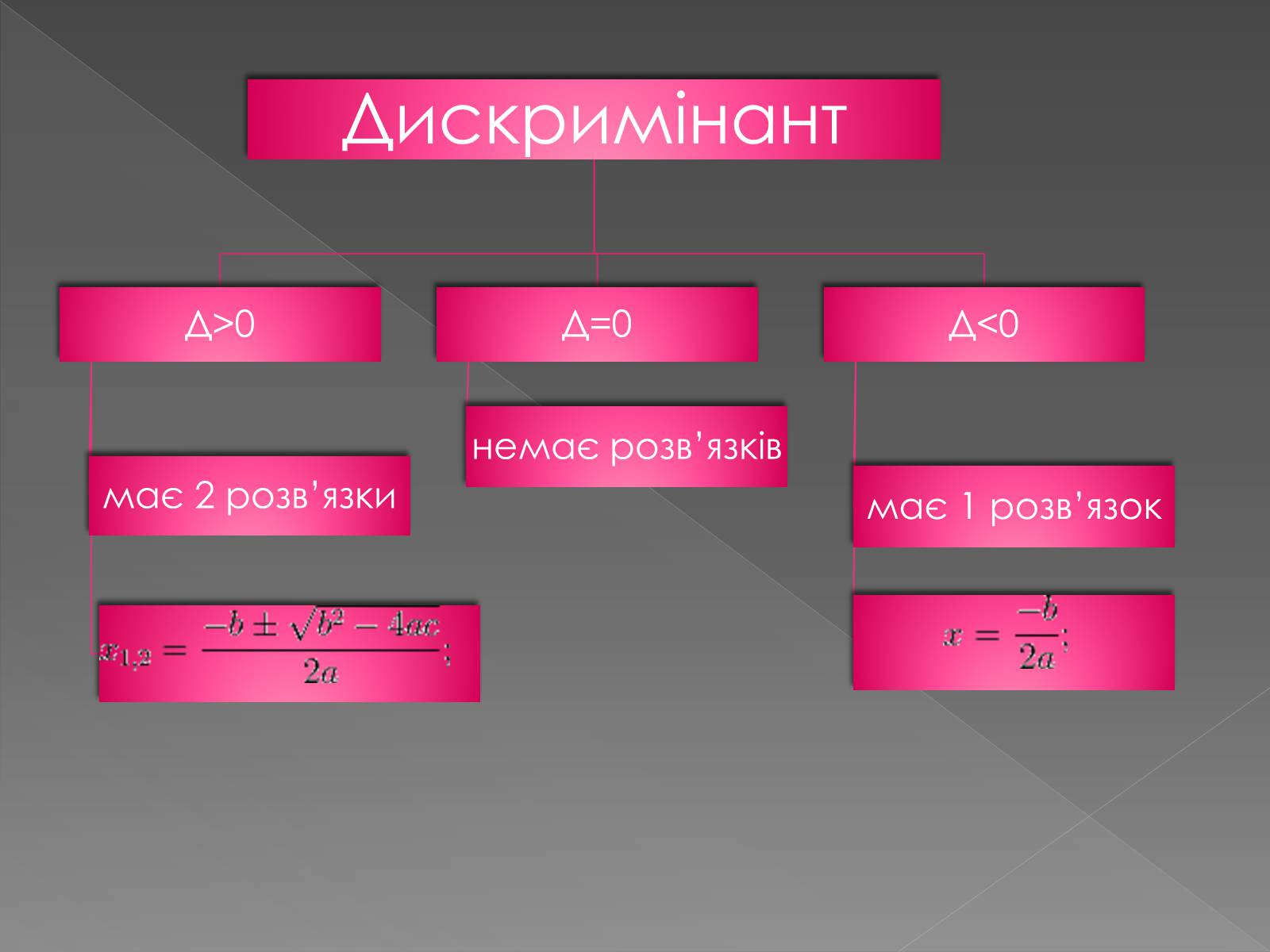
Що показує дискримінант?
Дискримінант показує кількість (наявність) коренів квадратного рівняння.
Дискримінант показує кількість (наявність) коренів квадратного рівняння.

Слайд #10
Що показує дискримінант?
Дискримінант показує кількість (наявність) коренів квадратного рівняння.
Дискримінант показує кількість (наявність) коренів квадратного рівняння.
Слайд #11
Квадратне число, яке має друге парне число
Якщо квадратне рівняння ах²+bх+с=0, має друге парне число, то
b- парне число
b=2m
m= b/2
D1=D/4=m²-ac
Якщо квадратне рівняння ах²+bх+с=0, має друге парне число, то
b- парне число
b=2m
m= b/2
D1=D/4=m²-ac

Слайд #12
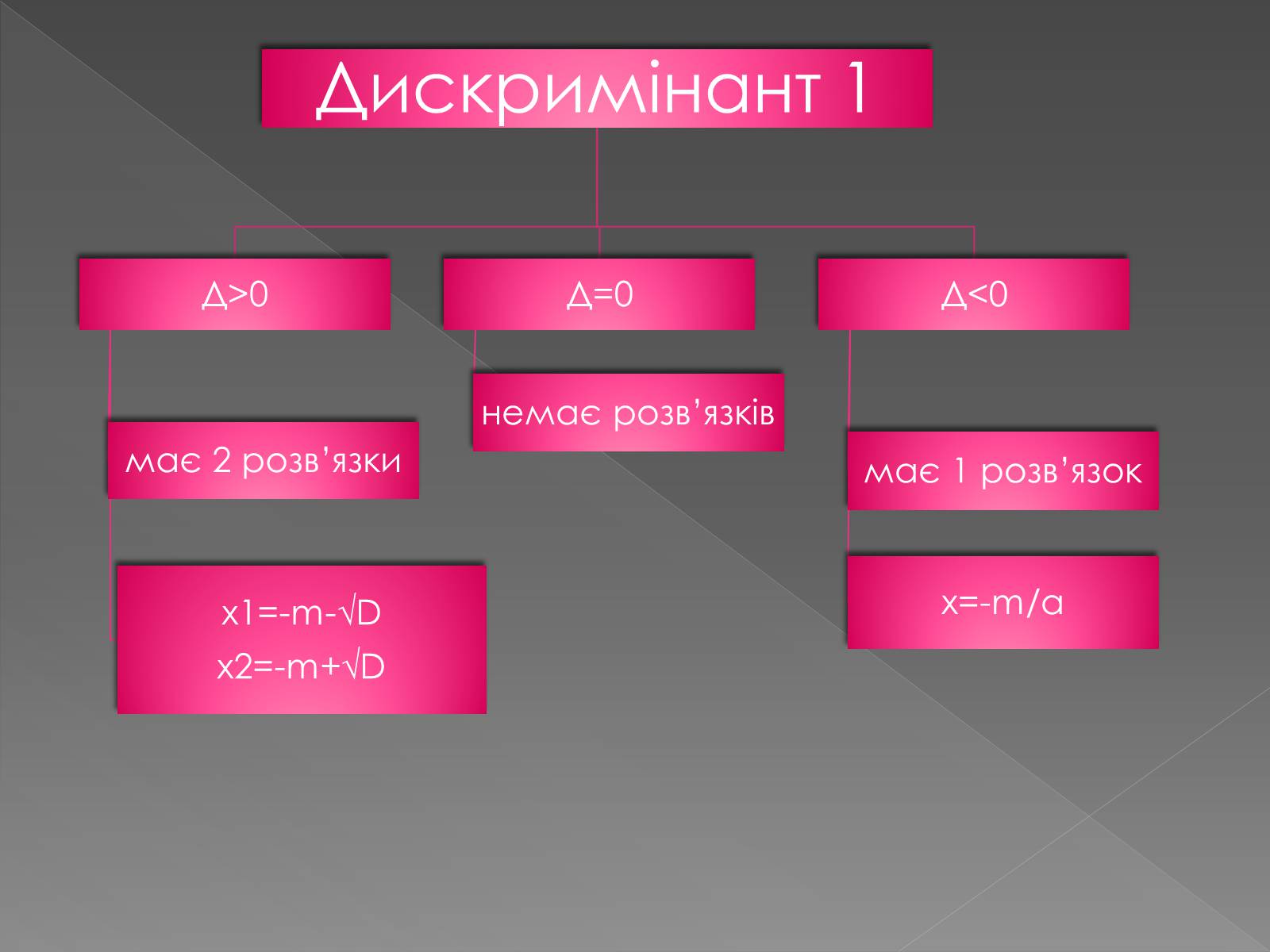
Квадратне число, яке має друге парне число
Якщо квадратне рівняння ах²+bх+с=0, має друге парне число, то
b- парне число
b=2m
m= b/2
D1=D/4=m²-ac
Якщо квадратне рівняння ах²+bх+с=0, має друге парне число, то
b- парне число
b=2m
m= b/2
D1=D/4=m²-ac
Слайд #13
Теорема Вієта для повного квадратного рівняння
ax²+bx+c=0
x1*x2=c/a
x1+x2= -b/aАле за оберненою теоремою, до теореми Вієта легше розв'язувати рівняння
x²+mx+p=0
x1*x2=p
x1+x2=-m
ax²+bx+c=0
x1*x2=c/a
x1+x2= -b/aАле за оберненою теоремою, до теореми Вієта легше розв'язувати рівняння
x²+mx+p=0
x1*x2=p
x1+x2=-m

Слайд #14
Розв'яжіть рівняння
x²-22x-22=0 0.2y²-0.4y+7=0
4x²-6x+3=0 3x²-2x-1=0
2x²-x+3=0 3y²-5y+1=0
x²-4x-5=0 x²-12x+36=0
6x²+36=0 x²-x-36=0
x²-22x-22=0 0.2y²-0.4y+7=0
4x²-6x+3=0 3x²-2x-1=0
2x²-x+3=0 3y²-5y+1=0
x²-4x-5=0 x²-12x+36=0
6x²+36=0 x²-x-36=0

Слайд #15
Дякую за увагу
