Презентація на тему «Правильні многогранники» (варіант 2)
390
Слайд #1
Тема уроку“Правильні многогранники”
Мета уроку:сформувати поняття правильного многогранника, ознайомити учнів з основними видами правильних многогранників, дослідити їх властивості та зв'язок з навколишнім середовищем
Тип уроку :урок засвоєння нових знань, вироблення первинних вмінь
1
“ Математика здає свої фортеці лише сильним, сміливим і кмітливим ”
А.Конфорович
Мета уроку:сформувати поняття правильного многогранника, ознайомити учнів з основними видами правильних многогранників, дослідити їх властивості та зв'язок з навколишнім середовищем
Тип уроку :урок засвоєння нових знань, вироблення первинних вмінь
1
“ Математика здає свої фортеці лише сильним, сміливим і кмітливим ”
А.Конфорович
Слайд #2
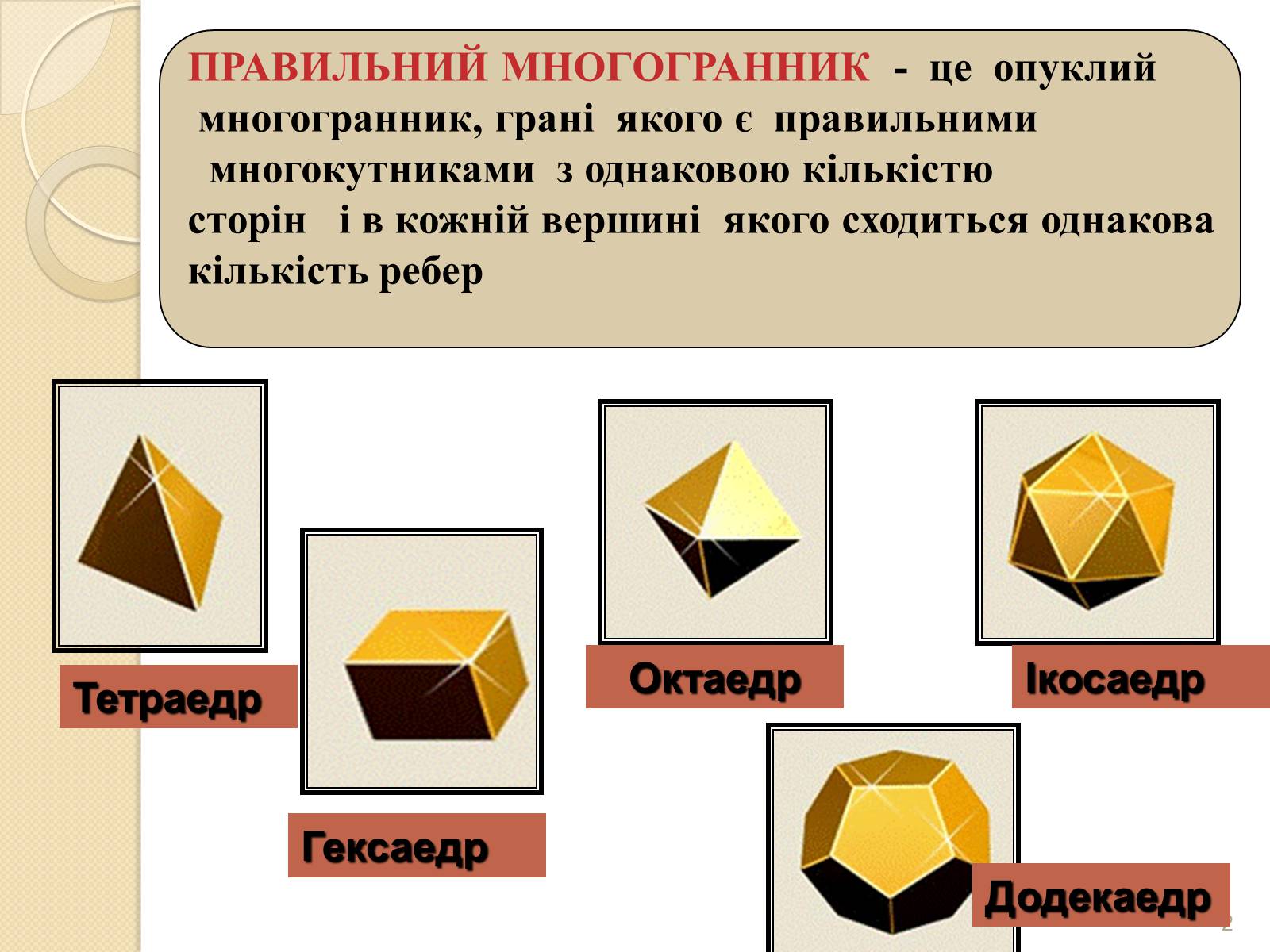
ПРАВИЛЬНИЙ МНОГОГРАННИК - це опуклий многогранник, грані якого є правильними многокутниками з однаковою кількістю сторін і в кожній вершині якого сходиться однакова кількість ребер
2
Тетраедр
Гексаедр
Октаедр
Ікосаедр
Додекаедр
2
Тетраедр
Гексаедр
Октаедр
Ікосаедр
Додекаедр
Слайд #3
Назва многогранника
І частина ІІ частина
«тетра» - 4
«гекса» - 6 «едра» - грань
«окта» - 8
«додека »-12
«ікоса» - 20
3
І частина ІІ частина
«тетра» - 4
«гекса» - 6 «едра» - грань
«окта» - 8
«додека »-12
«ікоса» - 20
3
Слайд #4
Платонові тіла
4
вогонь
тетраедр
вода
ікосаедр
повітря
октаеэдр
земля
гексаедр
всесвіт
додекаедр
4
вогонь
тетраедр
вода
ікосаедр
повітря
октаеэдр
земля
гексаедр
всесвіт
додекаедр
Слайд #5
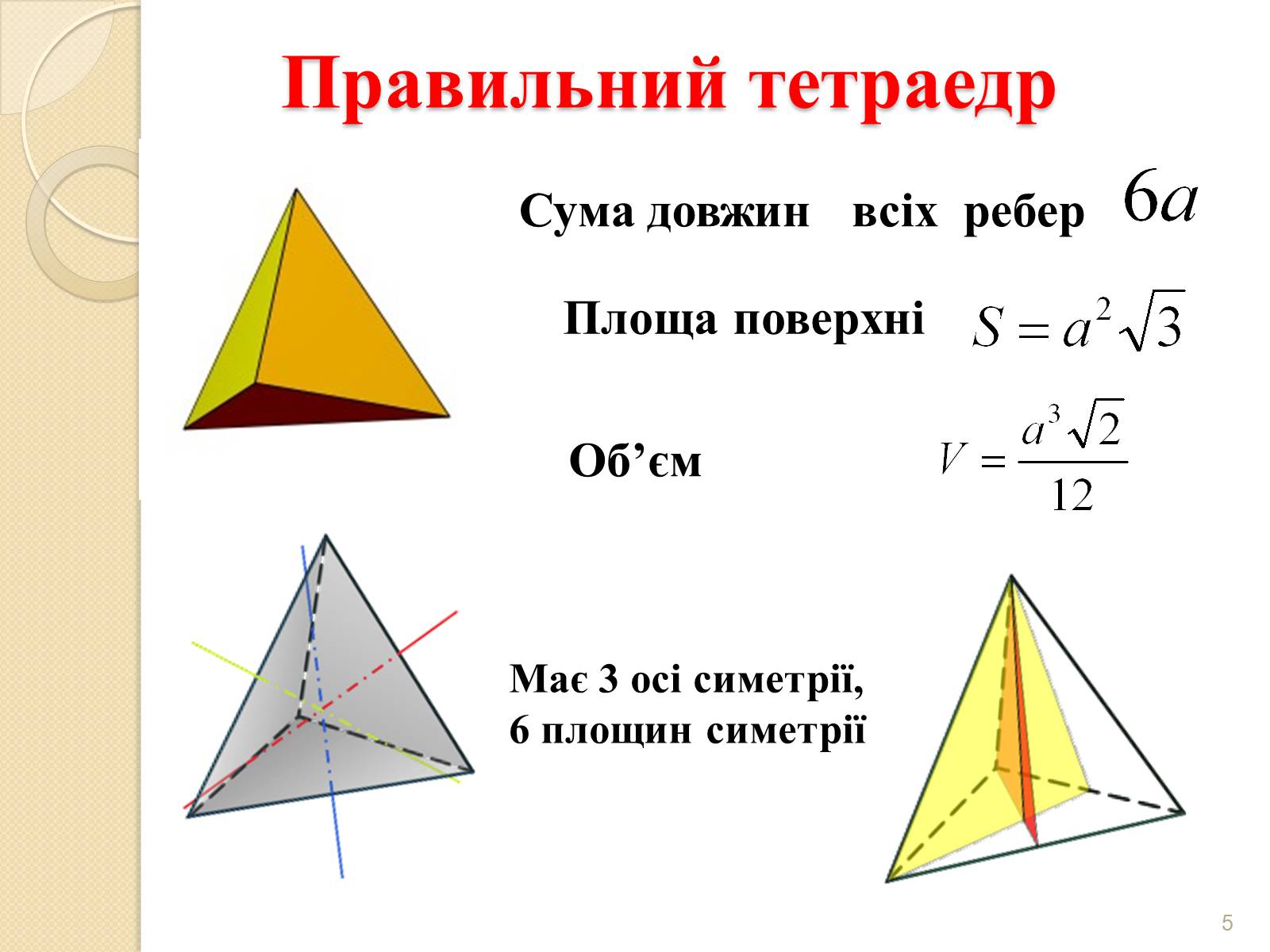
Правильний тетраедр
5
Має 3 осі симетрії,
6 площин симетрії
Сума довжин всіх ребер
Площа поверхні
Об'єм
5
Має 3 осі симетрії,
6 площин симетрії
Сума довжин всіх ребер
Площа поверхні
Об'єм
Слайд #6
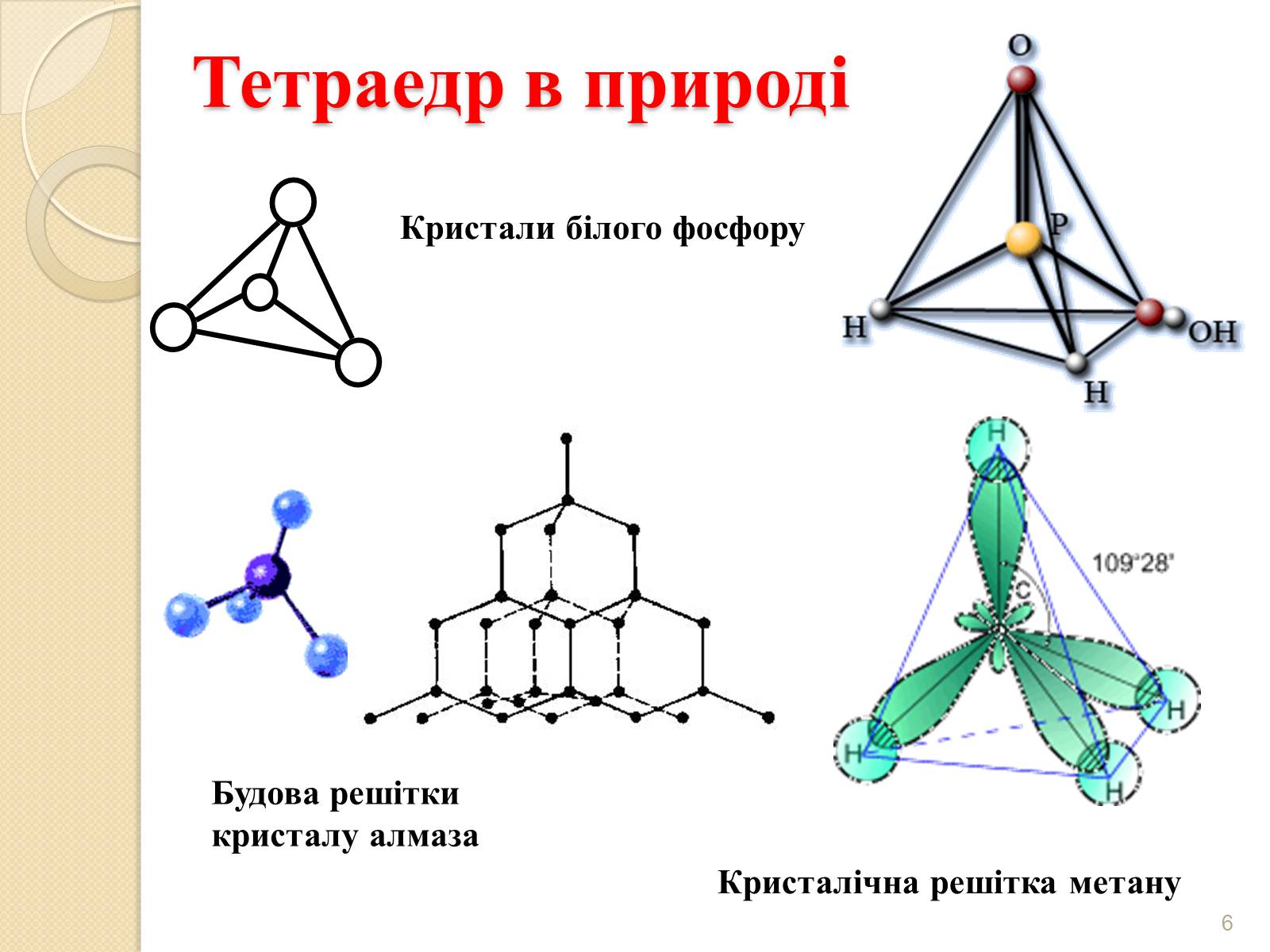
Тетраедр в природі
6
Кристали білого фосфору
Будова решітки кристалу алмаза
Кристалічна решітка метану
6
Кристали білого фосфору
Будова решітки кристалу алмаза
Кристалічна решітка метану
Слайд #7
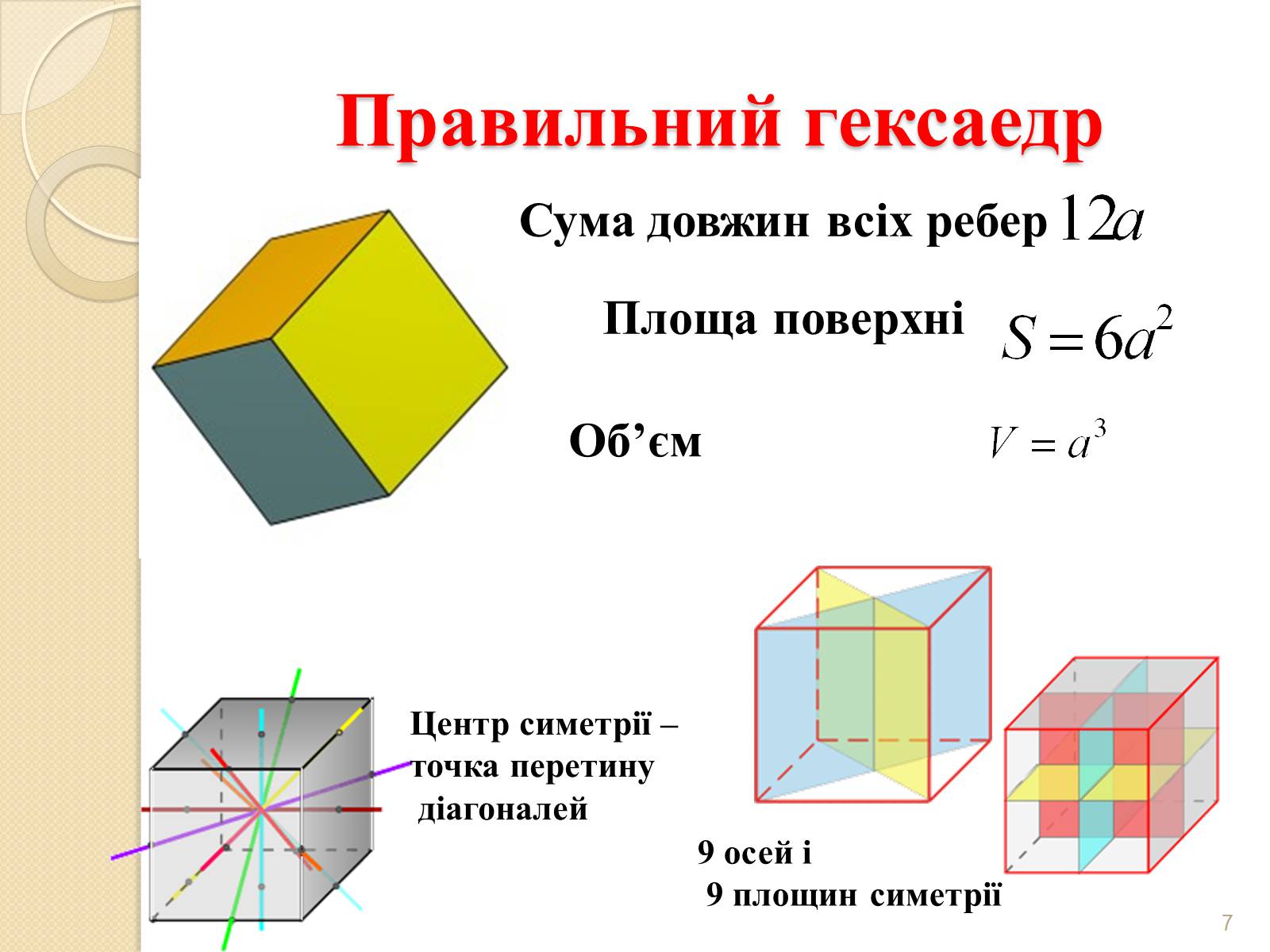
Правильний гексаедр
7
Центр симетрії –
точка перетину
діагоналей
9 осей і
9 площин симетрії
Сума довжин всіх ребер
Площа поверхні
Об'єм
7
Центр симетрії –
точка перетину
діагоналей
9 осей і
9 площин симетрії
Сума довжин всіх ребер
Площа поверхні
Об'єм
Слайд #8
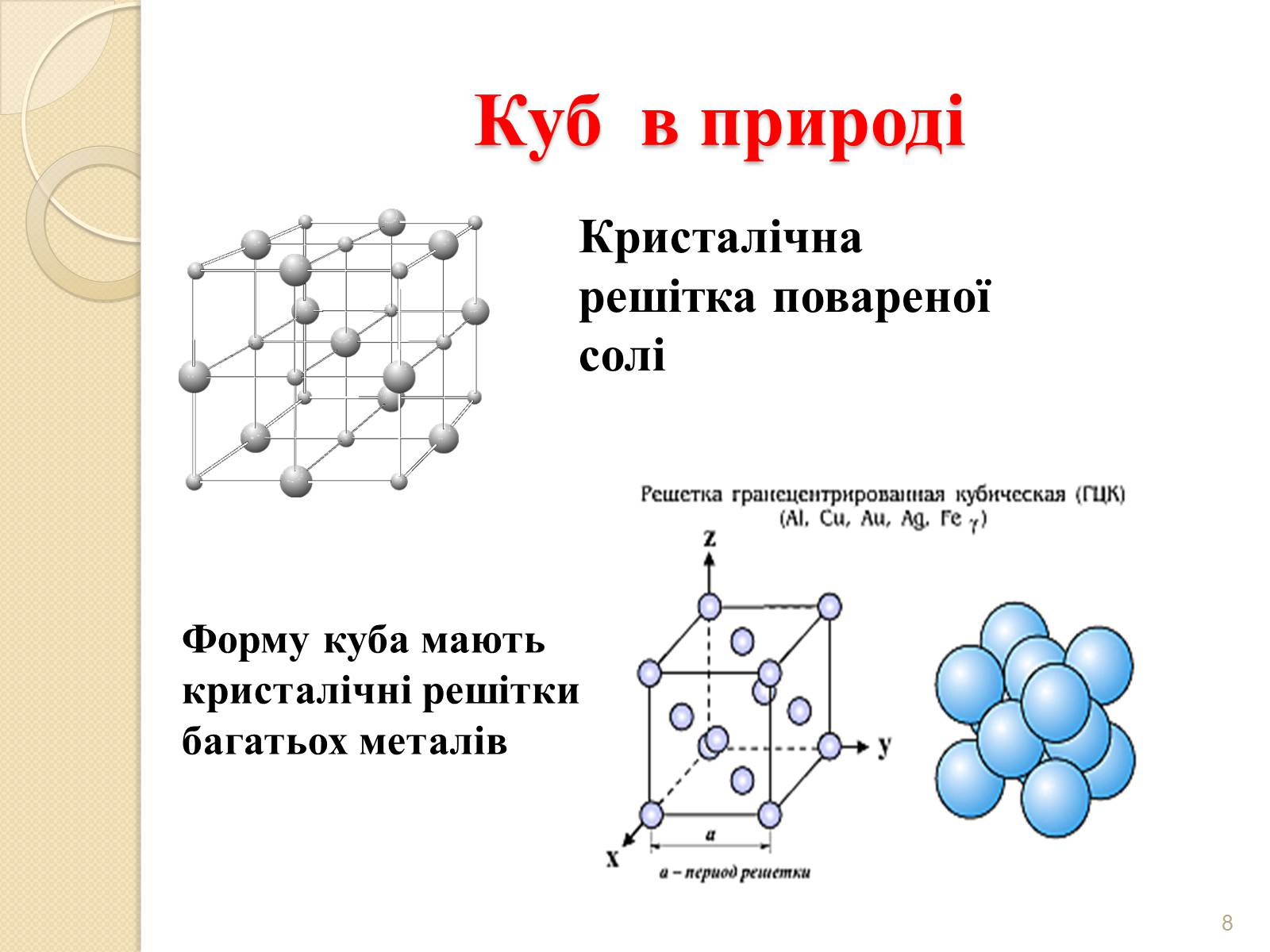
Куб в природі
8
Кристалічна решітка повареної солі
Форму куба мають кристалічні решітки багатьох металів
8
Кристалічна решітка повареної солі
Форму куба мають кристалічні решітки багатьох металів
Слайд #9
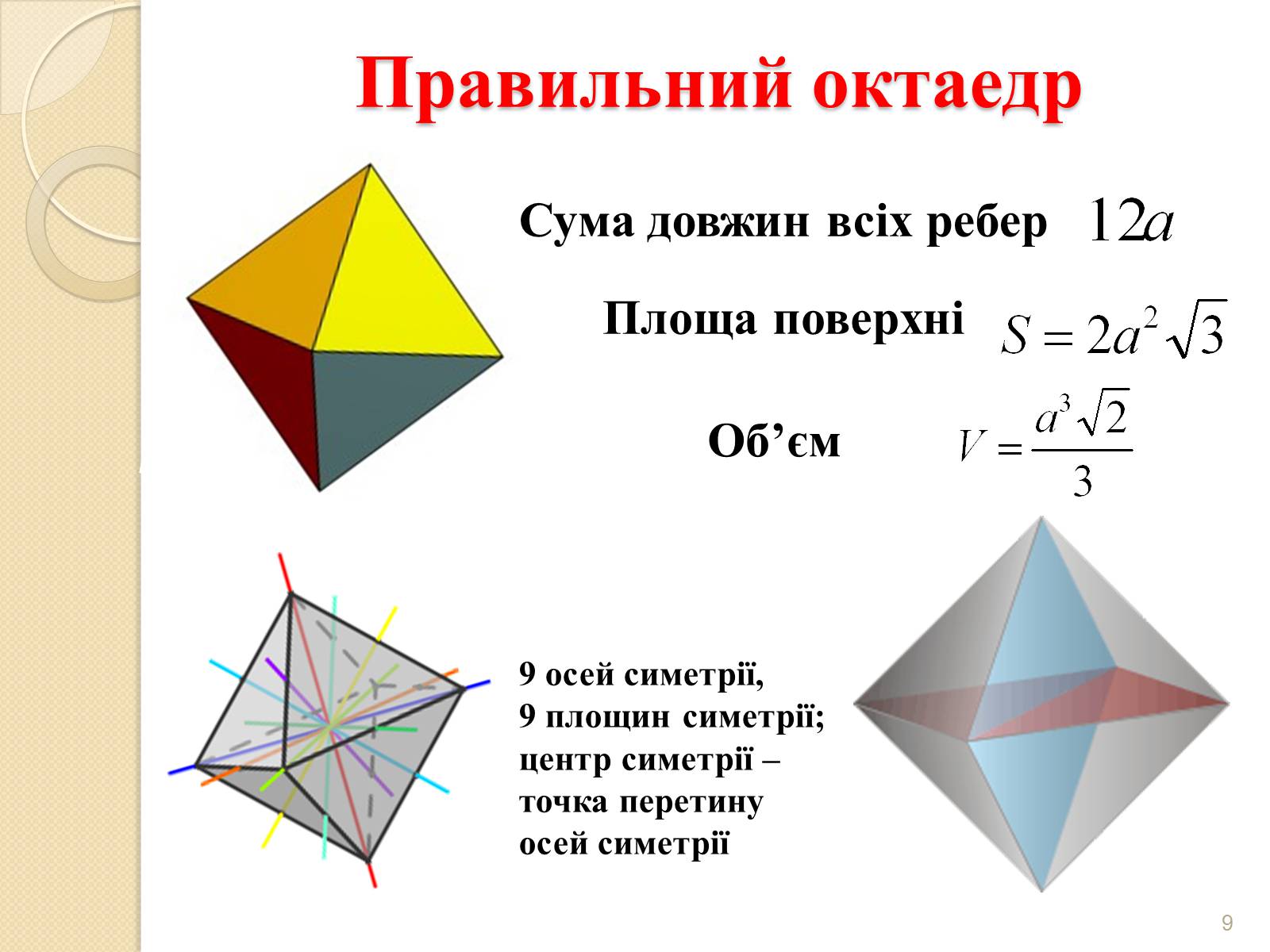
Правильний октаедр
9
Сума довжин всіх ребер
Площа поверхні
Об'єм
9 осей симетрії,
9 площин симетрії;
центр симетрії – точка перетину осей симетрії
9
Сума довжин всіх ребер
Площа поверхні
Об'єм
9 осей симетрії,
9 площин симетрії;
центр симетрії – точка перетину осей симетрії
Слайд #10
Октаедр в природі
10
Вуглець С характеризується структурою октаедра
Кристали алмаза
10
Вуглець С характеризується структурою октаедра
Кристали алмаза
Слайд #11
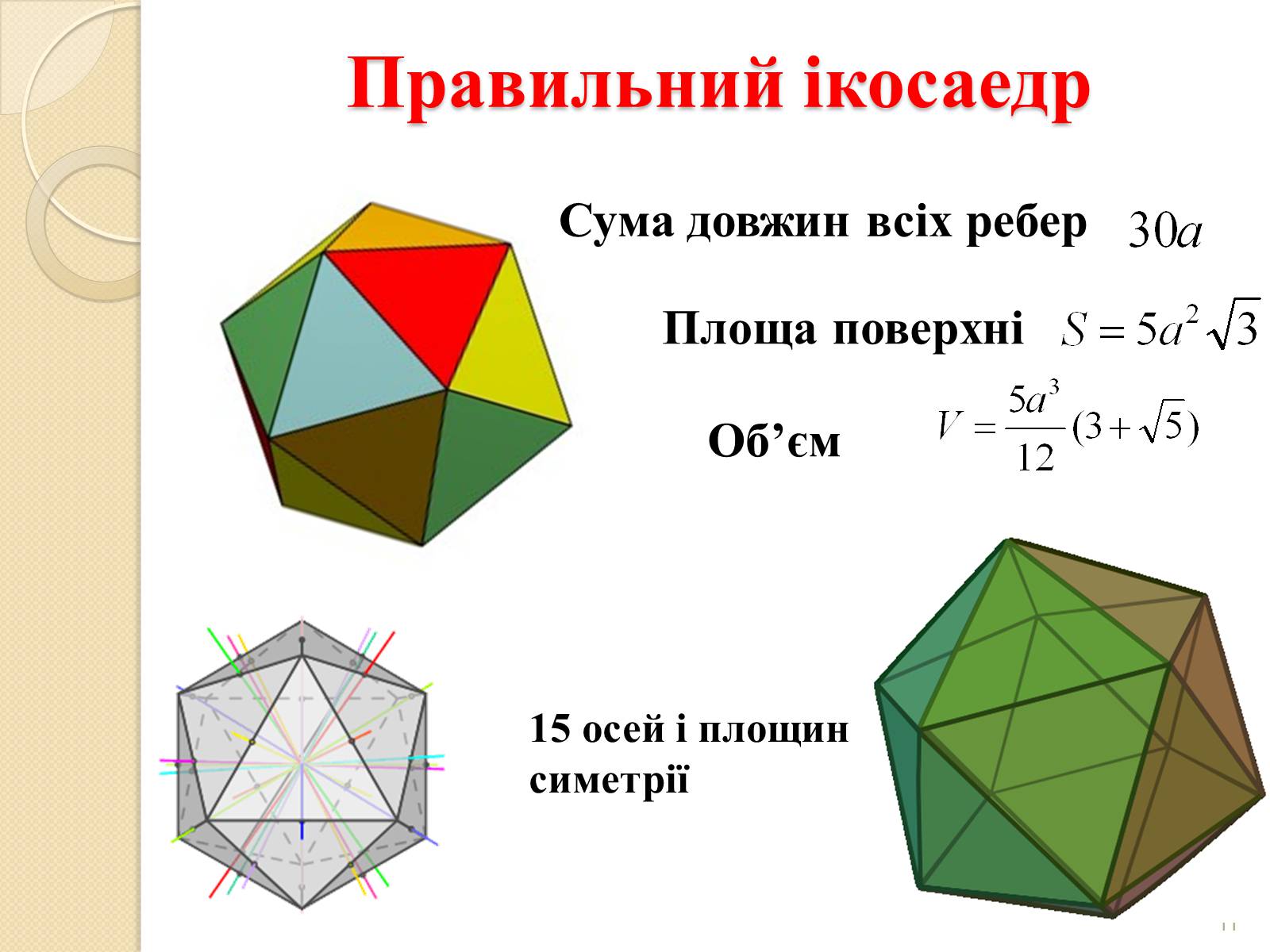
Правильний ікосаедр
11
15 осей і площин симетрії
Сума довжин всіх ребер
Площа поверхні
Об'єм
11
15 осей і площин симетрії
Сума довжин всіх ребер
Площа поверхні
Об'єм
Слайд #12
Ікосаедр в природі
12
Кристал бору має форму ікосаедра
У біології німецький біолог
початку ХХ століття Еге Геккель
дослідив,що одноклітинні
організми – феодарії, точно
передають форму ікосаедра
У фізиці капсиди багатьох вірусів (наприклад бактеріофаги, мімівірус)
12
Кристал бору має форму ікосаедра
У біології німецький біолог
початку ХХ століття Еге Геккель
дослідив,що одноклітинні
організми – феодарії, точно
передають форму ікосаедра
У фізиці капсиди багатьох вірусів (наприклад бактеріофаги, мімівірус)
Слайд #13
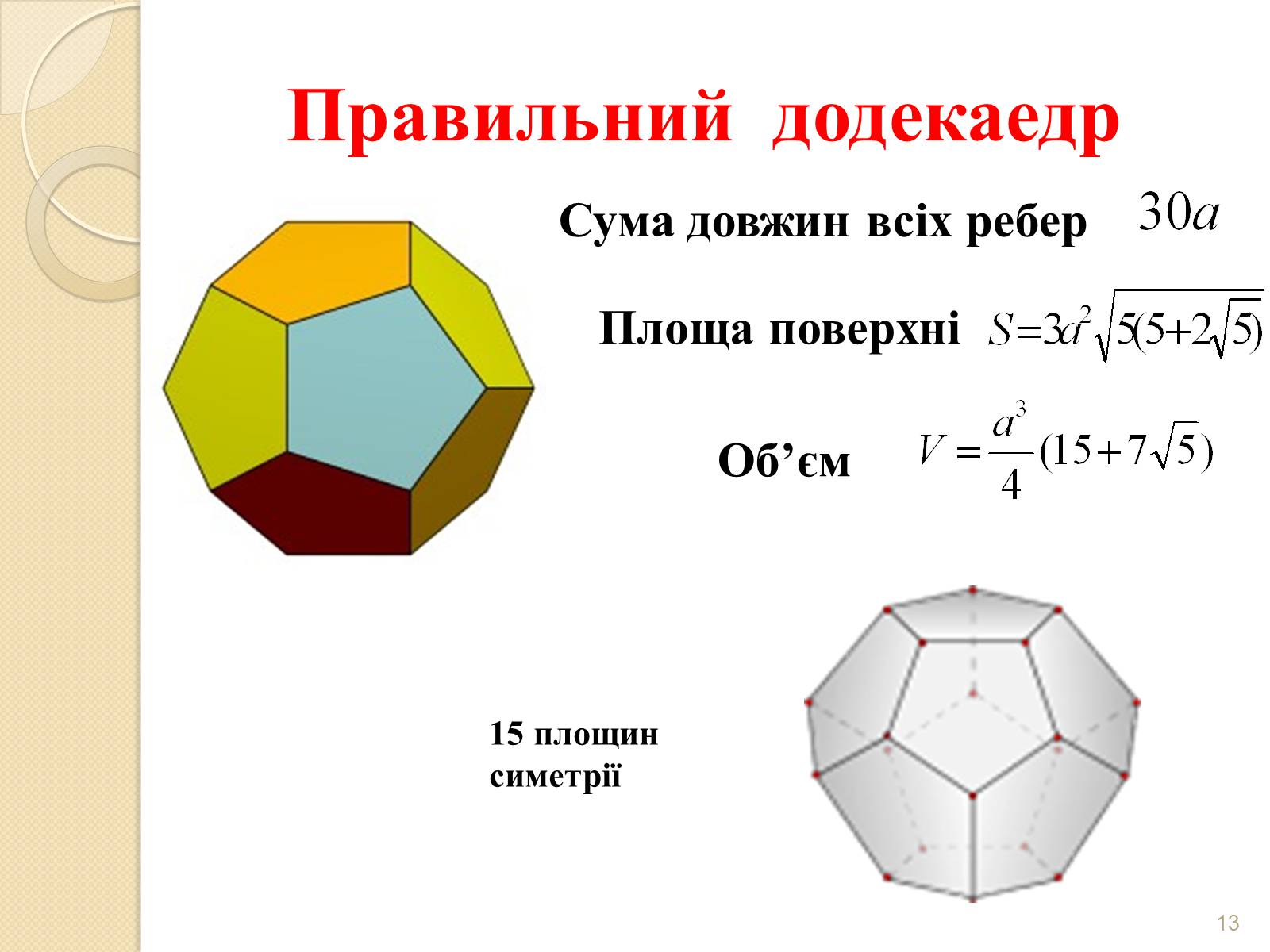
Правильний додекаедр
13
15 площин симетрії
Сума довжин всіх ребер
Площа поверхні
Об'єм
13
15 площин симетрії
Сума довжин всіх ребер
Площа поверхні
Об'єм
Слайд #14
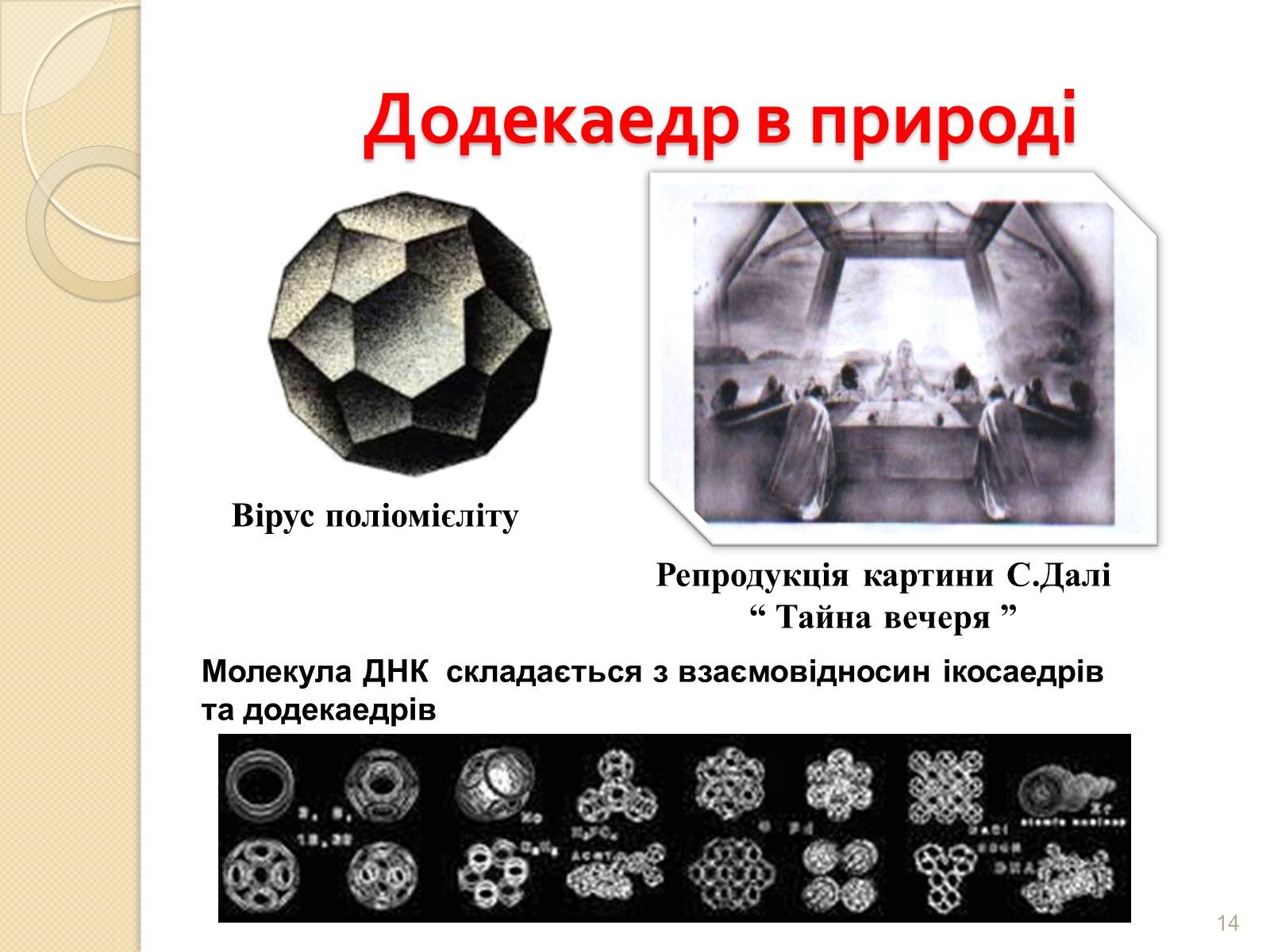
Додекаедр в природі
14
Вірус поліомієліту
Молекула ДНК складається з взаємовідносин ікосаедрів та додекаедрів
Репродукція картини С.Далі
“ Тайна вечеря ”
14
Вірус поліомієліту
Молекула ДНК складається з взаємовідносин ікосаедрів та додекаедрів
Репродукція картини С.Далі
“ Тайна вечеря ”
Слайд #15
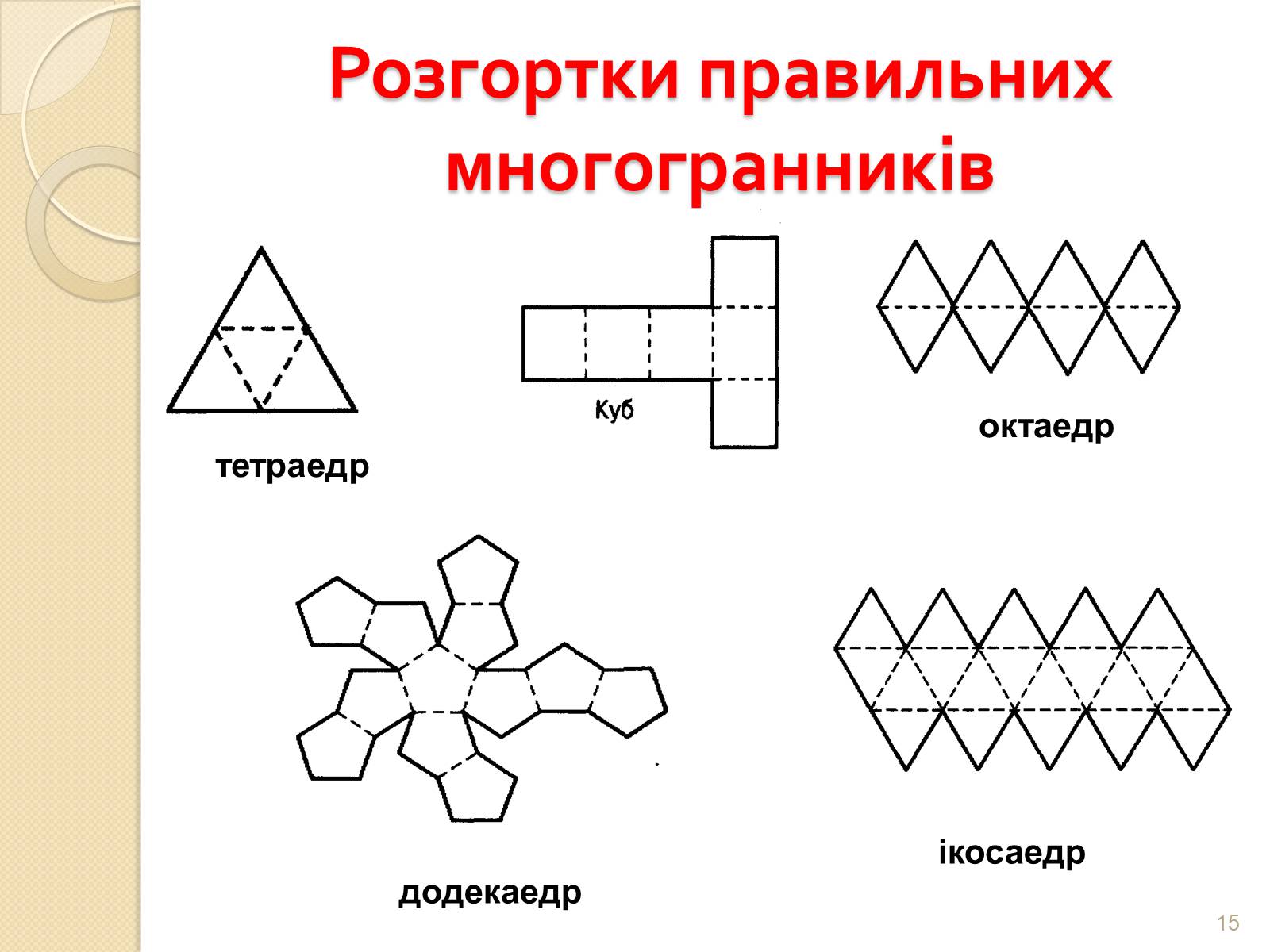
Розгортки правильних многогранників
15
тетраедр
октаедр
ікосаедр
додекаедр
15
тетраедр
октаедр
ікосаедр
додекаедр
Слайд #16
16
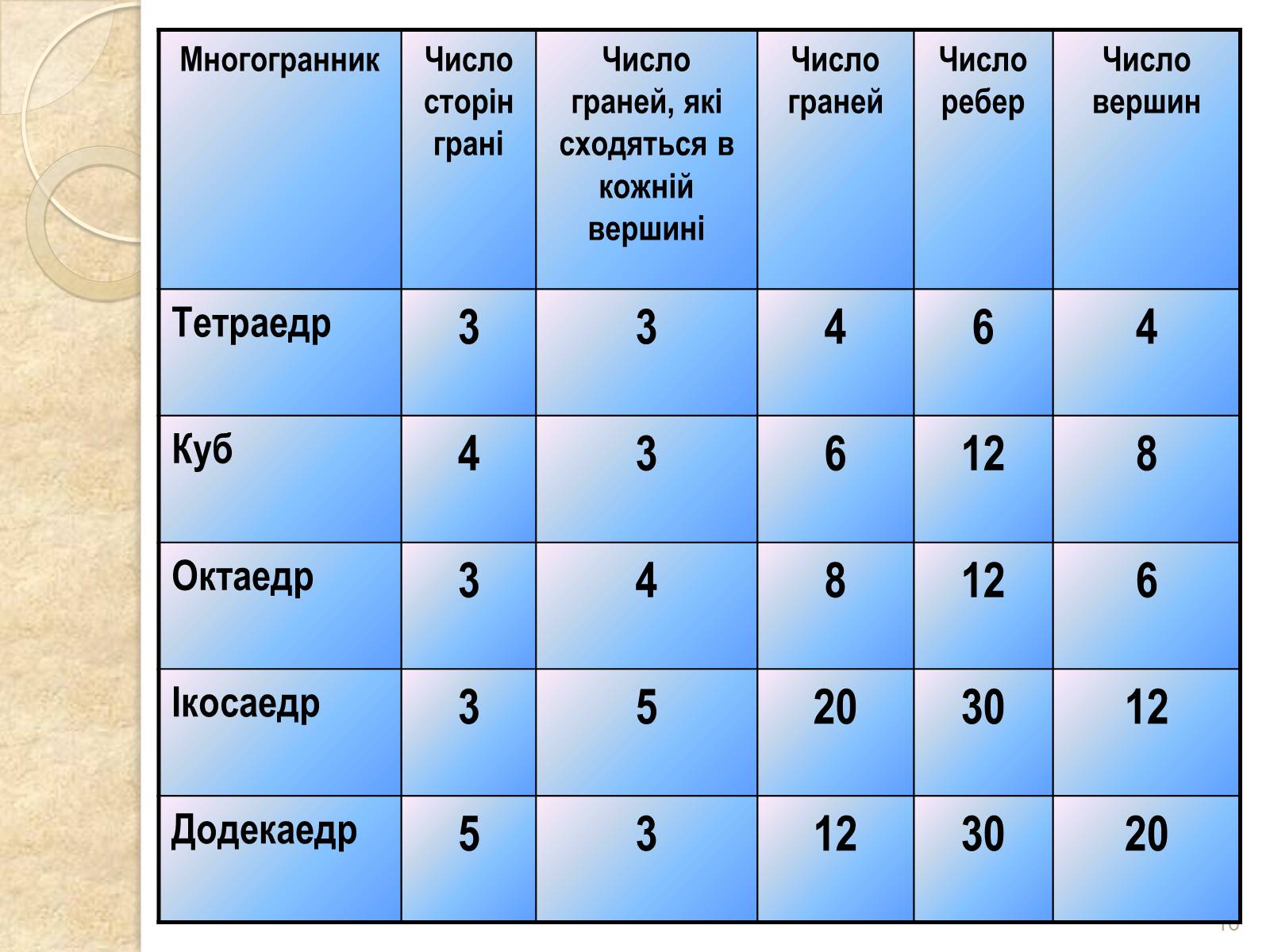
Многогранник
Число сторін грані
Число граней, які сходяться в кожній вершині
Число граней
Число ребер
Число вершин
Тетраедр
3
3
4
6
4
Куб
4
3
6
12
8
Октаедр
3
4
8
12
6
Ікосаедр
3
5
20
30
12
Додекаедр
5
3
12
30
20
Многогранник
Число сторін грані
Число граней, які сходяться в кожній вершині
Число граней
Число ребер
Число вершин
Тетраедр
3
3
4
6
4
Куб
4
3
6
12
8
Октаедр
3
4
8
12
6
Ікосаедр
3
5
20
30
12
Додекаедр
5
3
12
30
20
Слайд #17
Висновки
17
Число вершин плюс
число граней мінус
число ребер дорівнює два
Теорема Ейлера
В + Г – Р = 2
Леонард Ейлер(1707 – 1783 рр.)німецький математик и фізик
17
Число вершин плюс
число граней мінус
число ребер дорівнює два
Теорема Ейлера
В + Г – Р = 2
Леонард Ейлер(1707 – 1783 рр.)німецький математик и фізик
Слайд #18
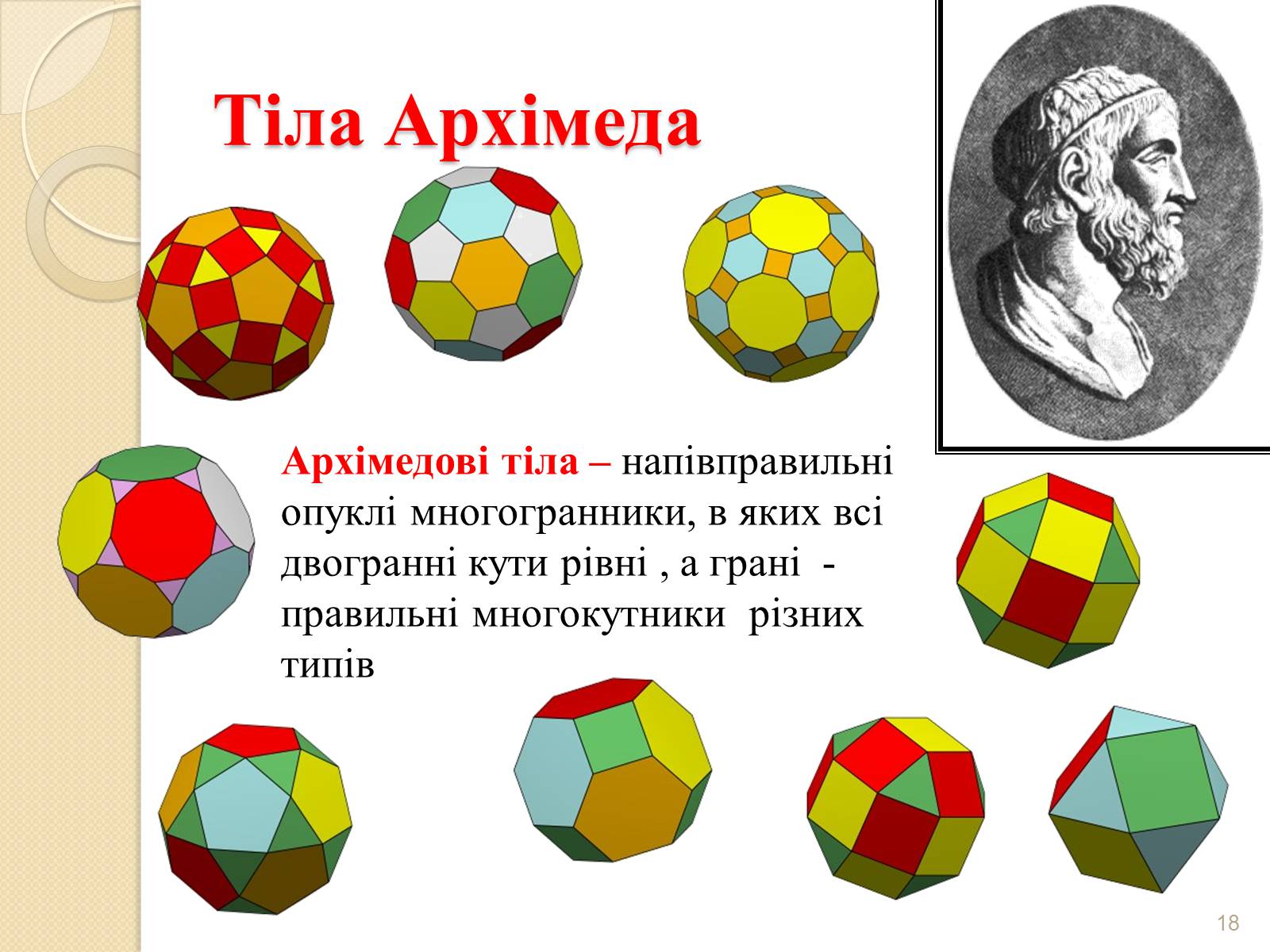
Тіла Архімеда
18
Архімедові тіла – напівправильні опуклі многогранники, в яких всі двогранні кути рівні , а грані - правильні многокутники різних типів
18
Архімедові тіла – напівправильні опуклі многогранники, в яких всі двогранні кути рівні , а грані - правильні многокутники різних типів
Слайд #19
Тіла Пуансона
19
Малий зірковий
додекаедр
Великий зірковий додекаедр
Великий додекаедр
Великий ікосаедр
19
Малий зірковий
додекаедр
Великий зірковий додекаедр
Великий додекаедр
Великий ікосаедр
