- Головна
- Готові шкільні презентації
- Презентація на тему «Застосування інтеграла в економіці»
Презентація на тему «Застосування інтеграла в економіці»
329
Слайд #1
Застосування інтеграла в економіці
Кузніцов Євгеній, 11 клас
Красилівськка ЗОШ №2
Кузніцов Євгеній, 11 клас
Красилівськка ЗОШ №2

Слайд #2
1
Визначити обсяг продукції, виробленої робітником за третю годину робочого дня, якщо продуктивність праці характеризується функцією f(t) = 3/(3t +1) + 4.
Визначити обсяг продукції, виробленої робітником за третю годину робочого дня, якщо продуктивність праці характеризується функцією f(t) = 3/(3t +1) + 4.

Слайд #3
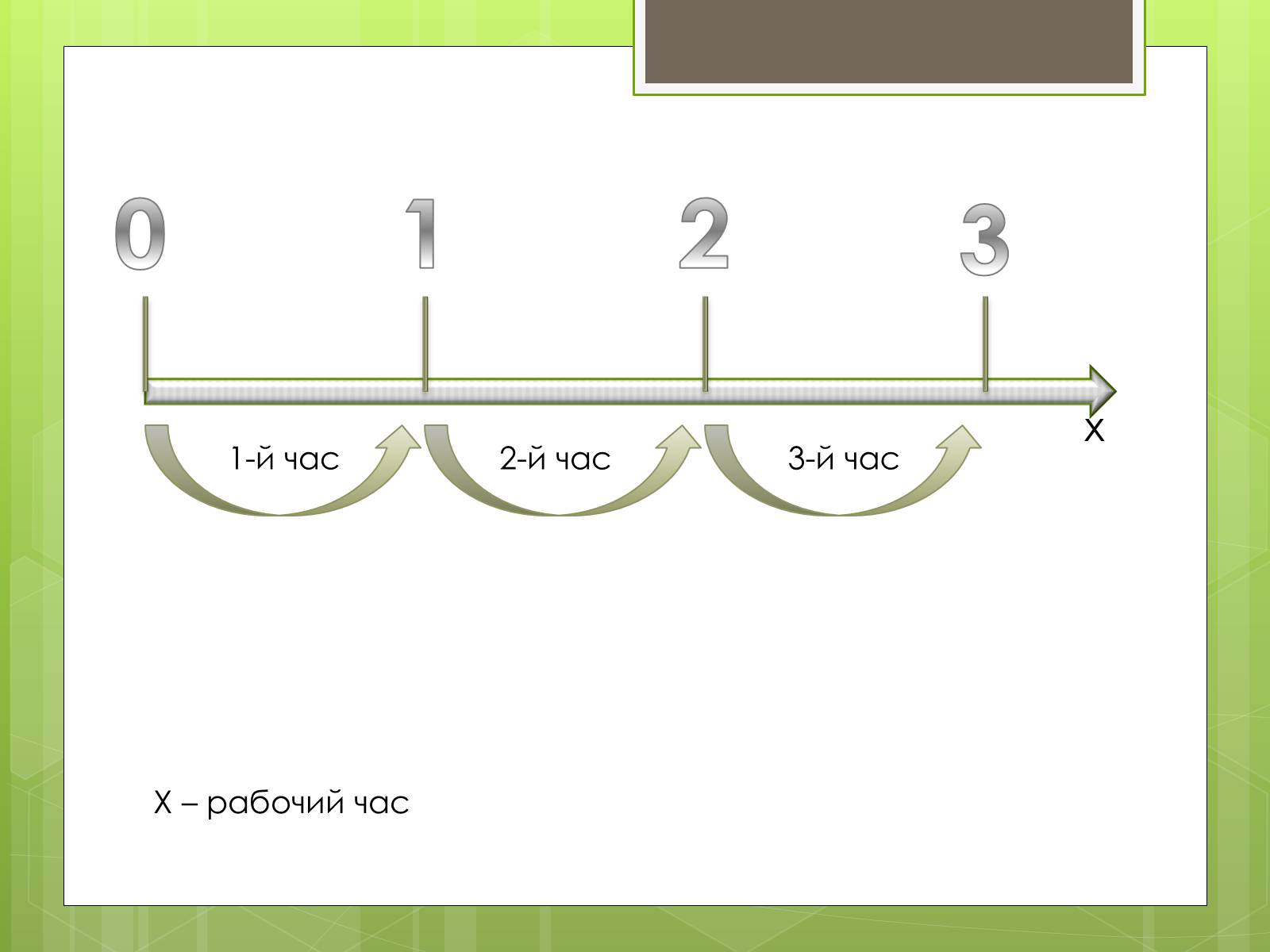
х
Х – рабочий час
1
2
3
3-й час
2-й час
1-й час
Х – рабочий час
1
2
3
3-й час
2-й час
1-й час
Слайд #4
РІШЕННЯ
Якщо f (t) характеризує продуктивність праці робітника залежно від (часу) t, то обсяг продукції, за часу від t1 до t2 буде виражатися формулою:
V=
=(ln(3t+1)+4t)
В нашому випадку:
=
= ln10/7 + 4
V
=dt
=ln10
+ 12
– ln7
– 8
Якщо f (t) характеризує продуктивність праці робітника залежно від (часу) t, то обсяг продукції, за часу від t1 до t2 буде виражатися формулою:
V=
=(ln(3t+1)+4t)
В нашому випадку:
=
= ln10/7 + 4
V
=dt
=ln10
+ 12
– ln7
– 8

Слайд #5
2
Визначити запас товарів у магазині, утворений за три дні, якщо надходження товарів характеризується функцією f(t) = 2t + 5.
Визначити запас товарів у магазині, утворений за три дні, якщо надходження товарів характеризується функцією f(t) = 2t + 5.

Слайд #6
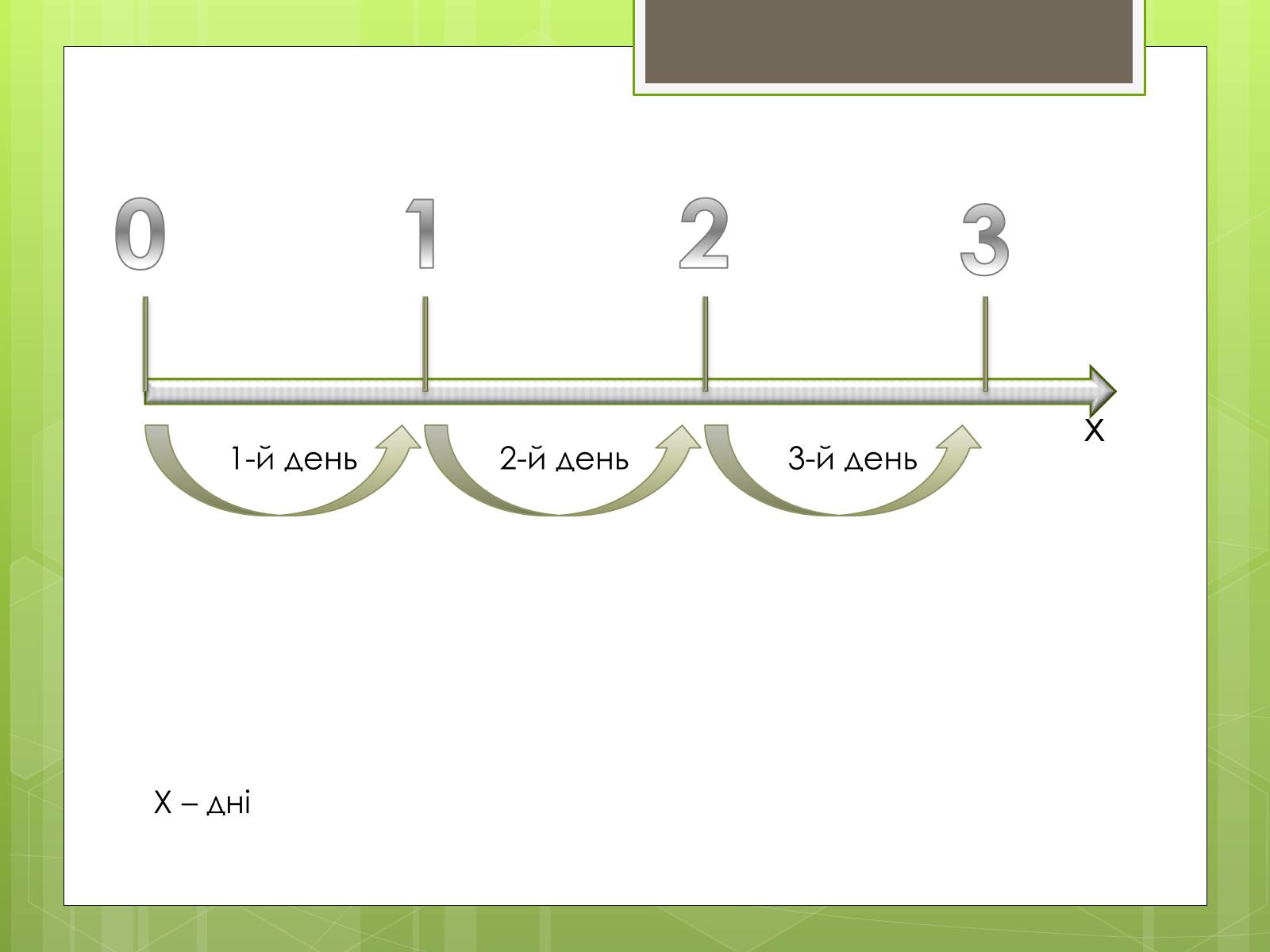
х
Х – дні
1
2
3
3-й день
2-й день
1-й день
Х – дні
1
2
3
3-й день
2-й день
1-й день
Слайд #7
Маємо:
V
=
=(
+ 5t)
= 9
+15
=24
=
=
- 0 - 0
РІШЕННЯ
V
=
=(
+ 5t)
= 9
+15
=24
=
=
- 0 - 0
РІШЕННЯ

Слайд #8
Завдання на визначення надлишку споживача.

Слайд #9
3
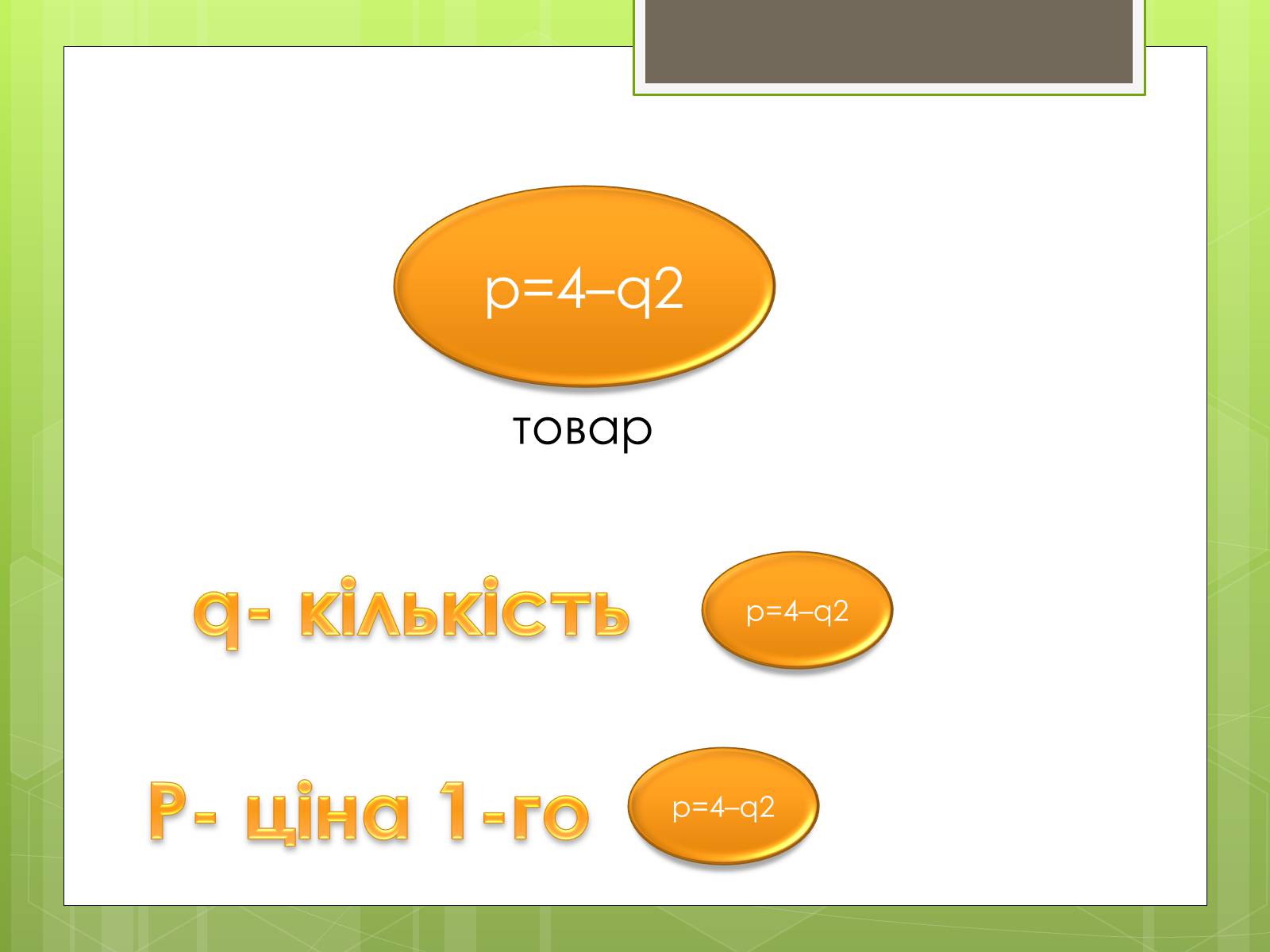
Відомо, що попит на деякий товар задається функцією p = 4-q2, де q-кількість товару (у шт.), P-ціна одиниці товару (у руб.), А рівновага на ринку даного товару досягається при p * = q * = 1. Визначте величину споживчого надлишку.
Відомо, що попит на деякий товар задається функцією p = 4-q2, де q-кількість товару (у шт.), P-ціна одиниці товару (у руб.), А рівновага на ринку даного товару досягається при p * = q * = 1. Визначте величину споживчого надлишку.

Слайд #10
p=4–q2
Р- ціна 1-го
q- кількість
p=4–q2
p=4–q2
товар
Р- ціна 1-го
q- кількість
p=4–q2
p=4–q2
товар
Слайд #11
РІШЕННЯ

Слайд #12
4
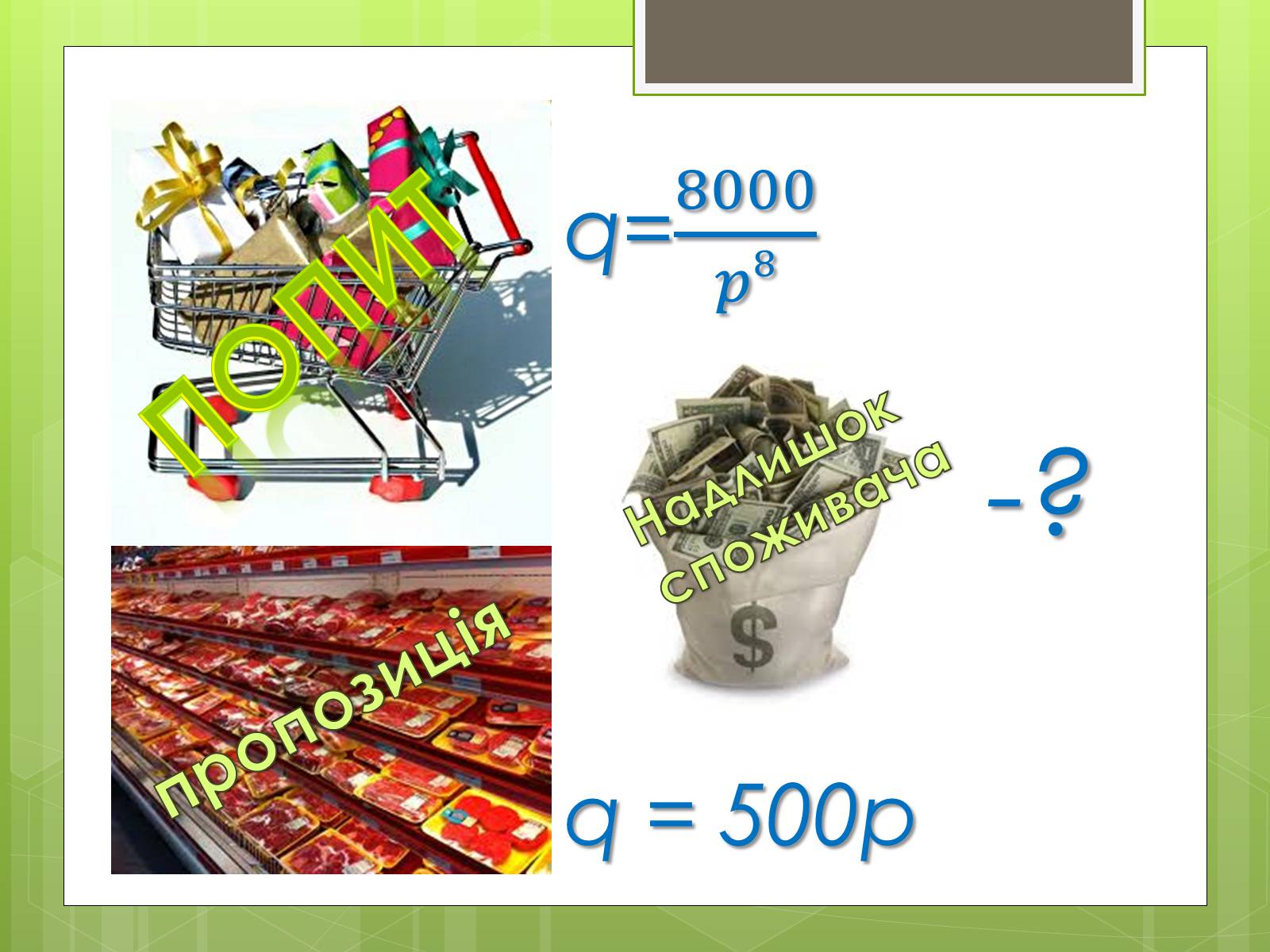
Відомо, що попит на деякий товар описується функцією q= а пропозиція даного товару характеризується функцією q = 500p. Знайдіть величину надлишку споживача при покупці даного товару.
Відомо, що попит на деякий товар описується функцією q= а пропозиція даного товару характеризується функцією q = 500p. Знайдіть величину надлишку споживача при покупці даного товару.

Слайд #13
попит
пропозиція
q=
q = 500p
Надлишок споживача
-?
пропозиція
q=
q = 500p
Надлишок споживача
-?
Слайд #14
1) Для розрахунку надлишку споживача спочатку визначимо параметри ринкової рівноваги(p*; q*):
p*=2
q*=1000
РІШЕННЯ
p*=2
q*=1000
РІШЕННЯ

Слайд #15
2) Формула для обчислення споживчого надлишку:
f(q)-обратная
т. е.
f(q)-обратная
т. е.

Слайд #16
5
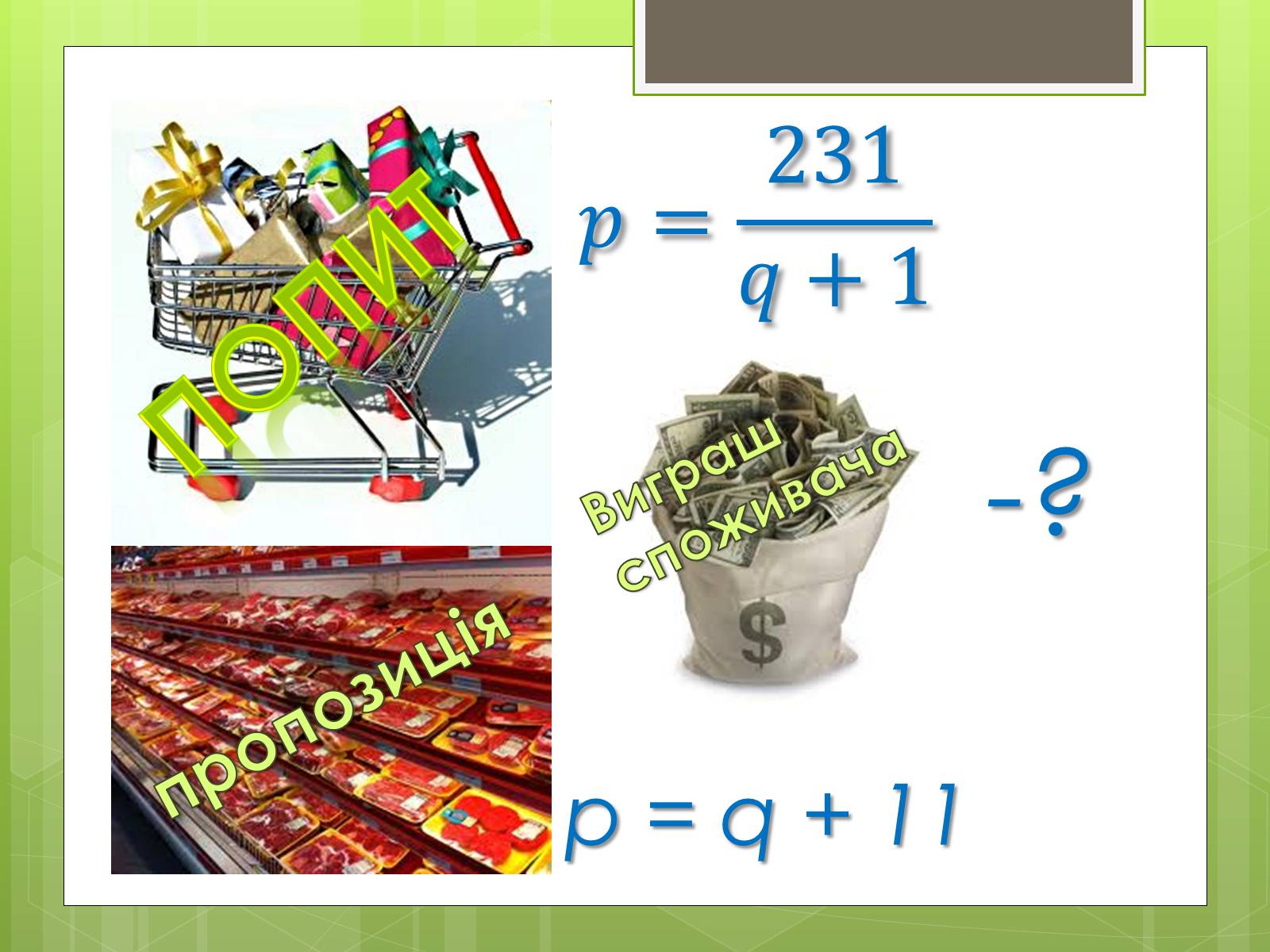
Відомо, що попит на деякий товар задається функцією пропозиція - функцією p = q + 11. Визначте величину виграшу споживача при покупці даного товару.
Відомо, що попит на деякий товар задається функцією пропозиція - функцією p = q + 11. Визначте величину виграшу споживача при покупці даного товару.

Слайд #17
попит
пропозиція
p = q + 11
Виграш споживача
-?
пропозиція
p = q + 11
Виграш споживача
-?
Слайд #18
1) Виграш споживача це споживчий надлишок. Для того, щоб знайти його, визначимо рівноважні значення кількості товару і його ціни:
,
,
.
РІШЕННЯ
,
,
.
РІШЕННЯ

Слайд #19
2) Порахуємо споживчий надлишок:

Слайд #20
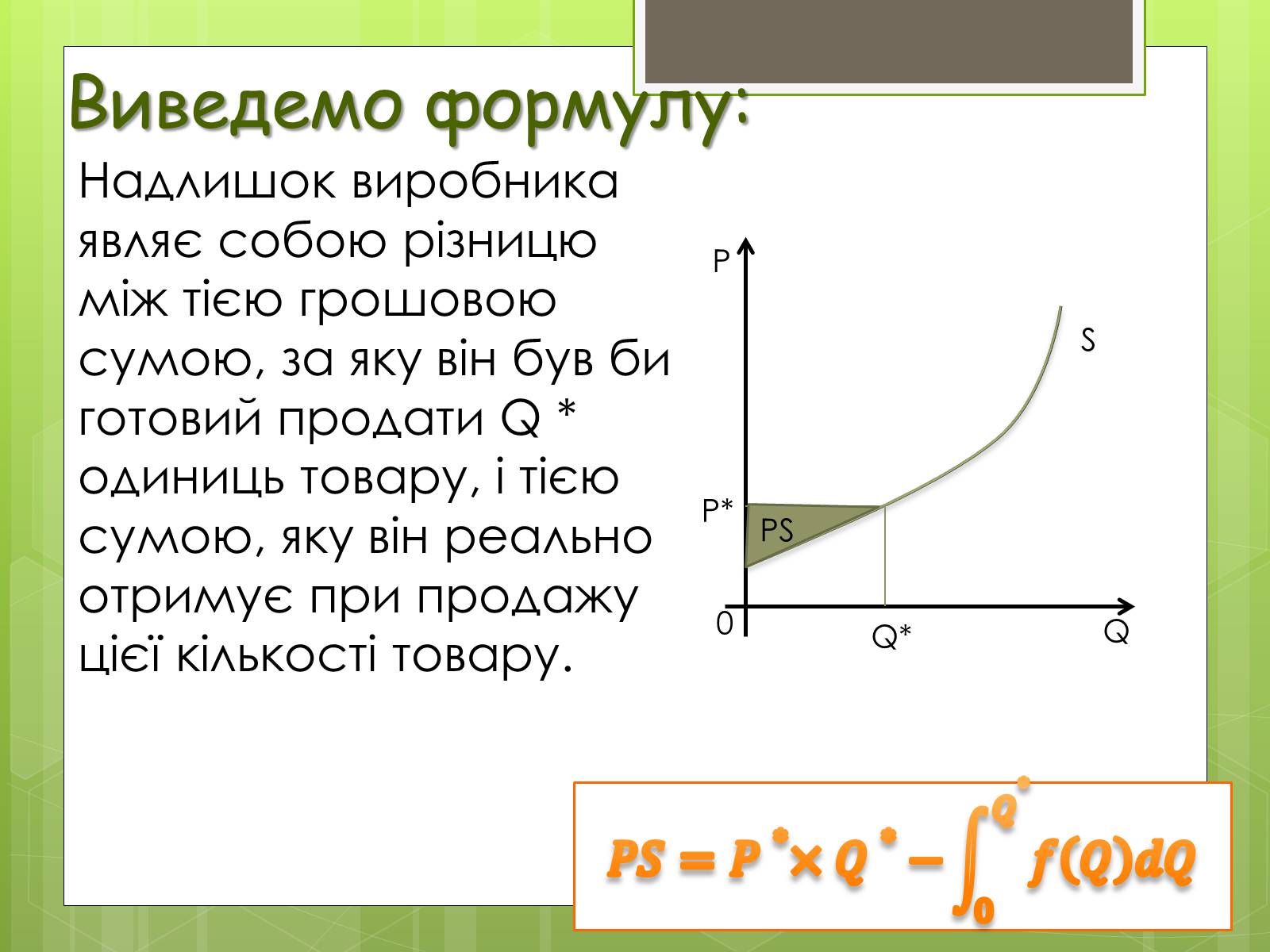
Надлишок виробника являє собою різницю між тією грошовою сумою, за яку він був би готовий продати Q * одиниць товару, і тією сумою, яку він реально отримує при продажу цієї кількості товару.
Виведемо формулу:
P
S
Q
Q*
P*
PS
Виведемо формулу:
P
S
Q
Q*
P*
PS
Слайд #21
6
Відомо, що крива пропозиції деякого товару має вигляд p = 4q3 + 2, а рівновага на ринку даного товару досягається при обсязі продажів Q* = 3. Визначте додаткову вигоду виробника при продажу такої кількості продукції.
Відомо, що крива пропозиції деякого товару має вигляд p = 4q3 + 2, а рівновага на ринку даного товару досягається при обсязі продажів Q* = 3. Визначте додаткову вигоду виробника при продажу такої кількості продукції.

Слайд #22
1) Знайдемо рівноважне значення ціни:
=
4+2
=110
2) Підставимо отримане значення в формулу:
РІШЕННЯ
=
4+2
=110
2) Підставимо отримане значення в формулу:
РІШЕННЯ

Слайд #23
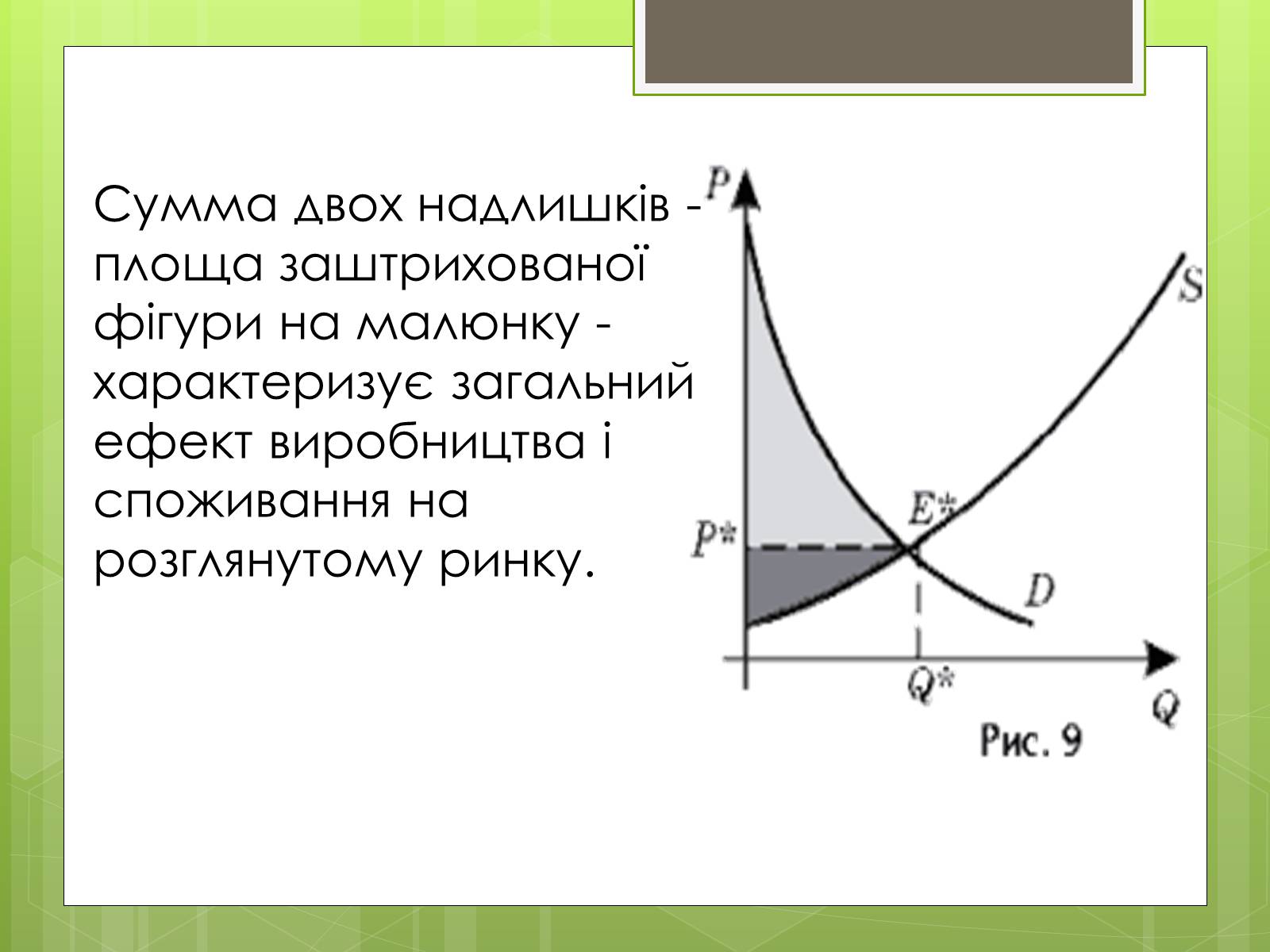
Cумма двох надлишків - площа заштрихованої фігури на малюнку - характеризує загальний ефект виробництва і споживання на розглянутому ринку.
Слайд #24
7
Дана крива попиту . Які грошові втрати споживача при введенні на даний товар податку з одиниці продажів у розмірі 1грн., Якщо відомо, що спочатку ринкова рівновага на даному ринку спостерігалося при ціні P*=2 руб.?
Дана крива попиту . Які грошові втрати споживача при введенні на даний товар податку з одиниці продажів у розмірі 1грн., Якщо відомо, що спочатку ринкова рівновага на даному ринку спостерігалося при ціні P*=2 руб.?

Слайд #25
I СПОСІБ
Для визначення споживчих втрат при збільшенні рівноважної ціни товару з 2 руб. до 3 руб. подивимося, як при цьому змінюється обсяг продажів:
РІШЕННЯ
Для визначення споживчих втрат при збільшенні рівноважної ціни товару з 2 руб. до 3 руб. подивимося, як при цьому змінюється обсяг продажів:
РІШЕННЯ

Слайд #26
=15 (руб.)

Слайд #27
II СПОСІБ
Так як в даному випадку функція попиту лінійна, то розглянуту ситуацію легко представити графічно:
C
14
16
20
Q
E
D
A
B
3
2
10
P
CS=
=15 (руб.)
Так як в даному випадку функція попиту лінійна, то розглянуту ситуацію легко представити графічно:
C
14
16
20
Q
E
D
A
B
3
2
10
P
CS=
=15 (руб.)

Слайд #28
8
Знайти обсяг продукції, виробленої за 4 роки, якщо функція Кобба - Дугласа має вигляд: z(t) = (1 + t)∙ e3t.
Знайти обсяг продукції, виробленої за 4 роки, якщо функція Кобба - Дугласа має вигляд: z(t) = (1 + t)∙ e3t.

Слайд #29
=
(ум. од.)
РІШЕННЯ

Слайд #30
9
За даними досліджень у розподілі доходів в одній з країн крива Джіні ОВА може бути описана рівнянням: у = 1- , де х - частка населення, у - частка доходів населення. Обчислити коефіцієнт Джинні.
За даними досліджень у розподілі доходів в одній з країн крива Джіні ОВА може бути описана рівнянням: у = 1- , де х - частка населення, у - частка доходів населення. Обчислити коефіцієнт Джинні.

Слайд #31
Для аналізу соціально - економічного будови суспільства використовується так звана «крива Джіні» (або «крива Лоренца») розподілу багатства в суспільстві.
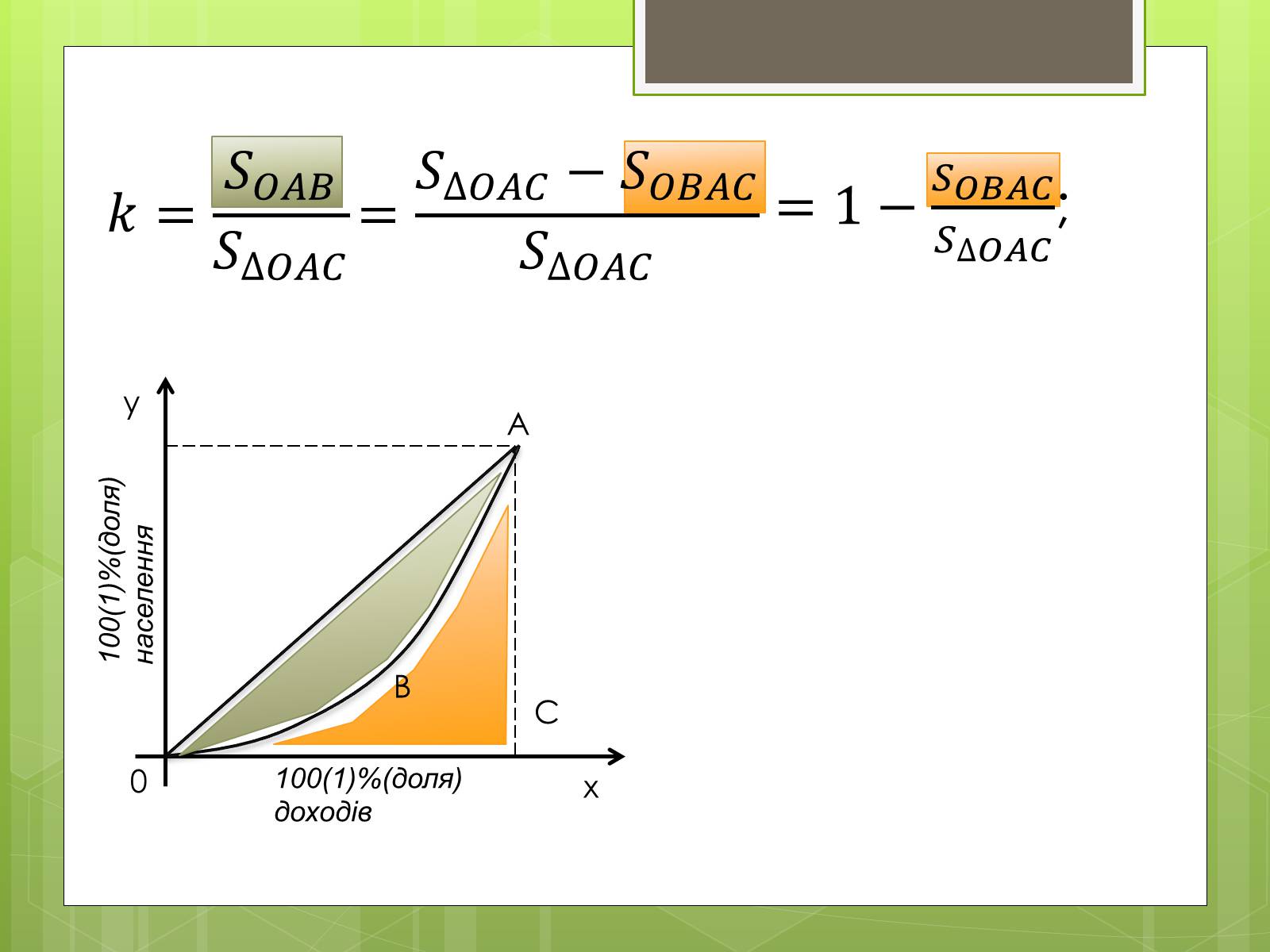
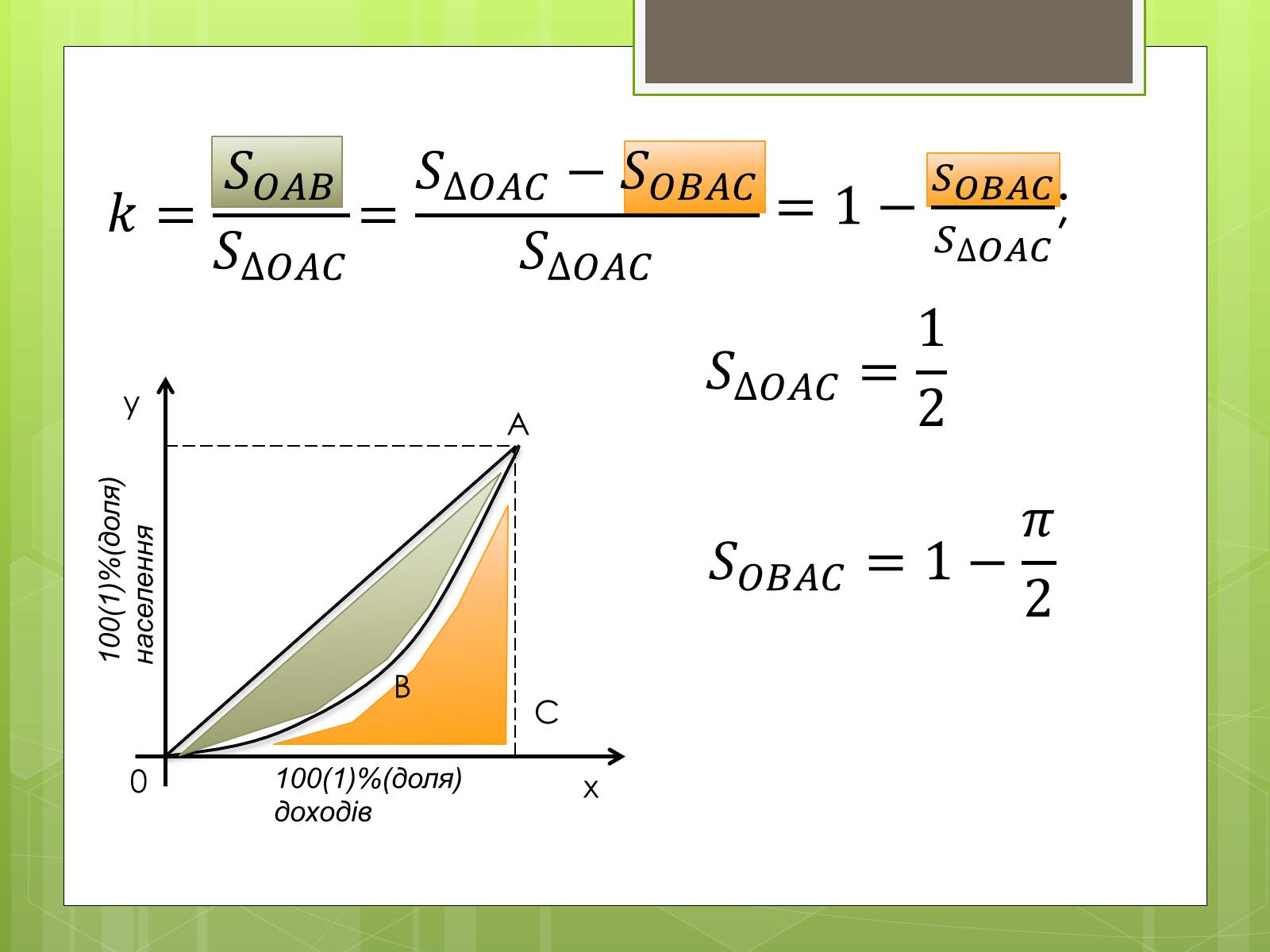
При рівномірному розподілі доходів крива Джіні виражається в пряму - бісектрису ОА, тому площа фігури ОАВ між бісектрисою ОА і кривою Джіні, віднесена до площі трикутника ОАС (коефіцієнт Джіні), характеризує ступінь нерівності в розподілі доходів населення.
РІШЕННЯ
При рівномірному розподілі доходів крива Джіні виражається в пряму - бісектрису ОА, тому площа фігури ОАВ між бісектрисою ОА і кривою Джіні, віднесена до площі трикутника ОАС (коефіцієнт Джіні), характеризує ступінь нерівності в розподілі доходів населення.
РІШЕННЯ

Слайд #32
;
A
x
C
B
y
100(1)%(доля) доходів
100(1)%(доля) населення
Слайд #33

Слайд #34
;
A
x
C
B
y
100(1)%(доля) доходів
100(1)%(доля) населення
Слайд #35
+
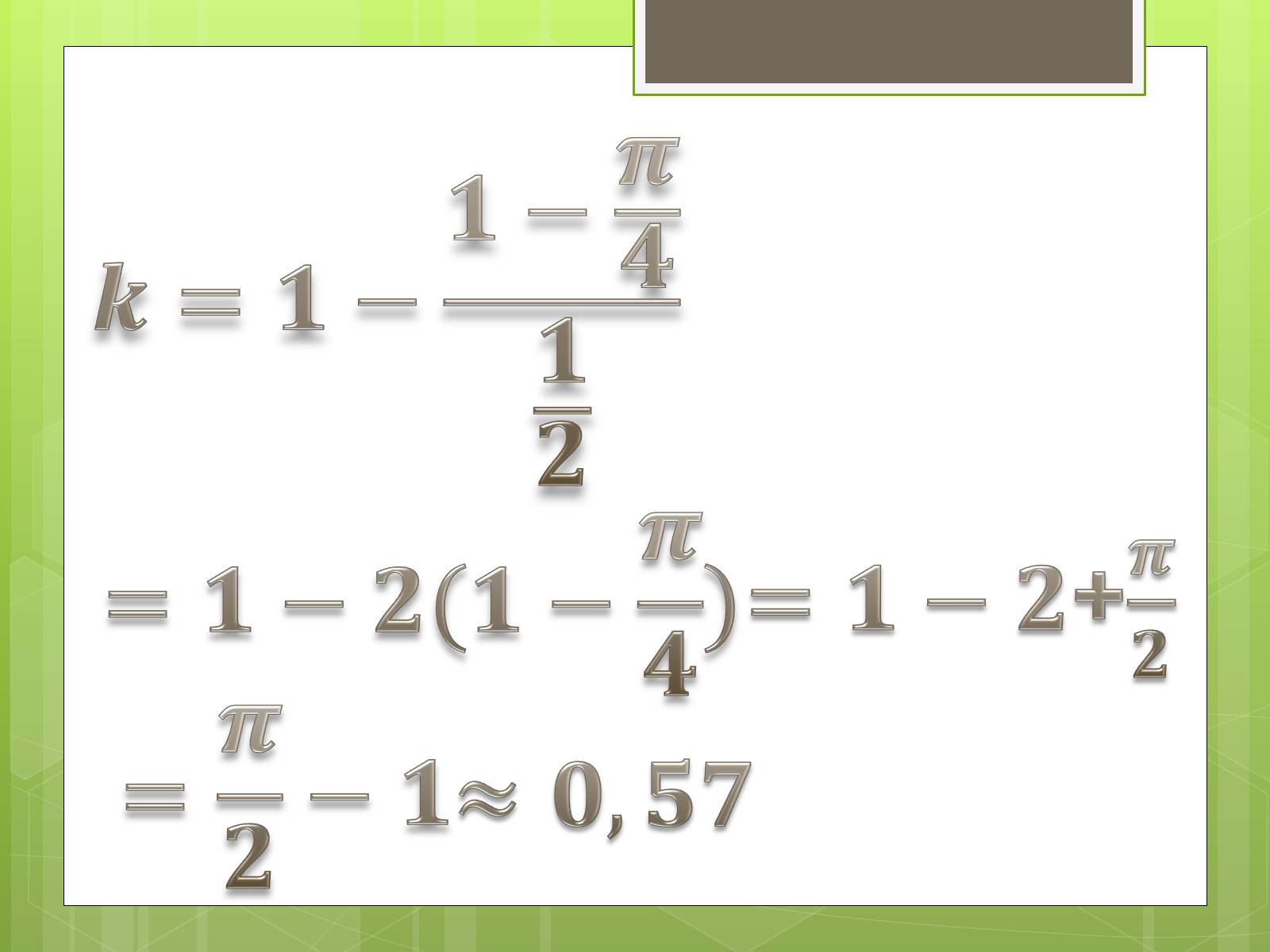
Слайд #36
10
Визначити дисконтований дохід за три роки при процентній ставці 8%, якщо початкові (базові) капіталовкладення склали 10млрд. руб. і намічається щорічно збільшувати капіталовкладення на 1млрд. руб.
Визначити дисконтований дохід за три роки при процентній ставці 8%, якщо початкові (базові) капіталовкладення склали 10млрд. руб. і намічається щорічно збільшувати капіталовкладення на 1млрд. руб.

Слайд #37
1
2
3
+1млрд.
+1млрд.
+1млрд.
8%
=10млрд.$
дисконтованний дохід за 3 роки - ?
2
3
+1млрд.
+1млрд.
+1млрд.
8%
=10млрд.$
дисконтованний дохід за 3 роки - ?

Слайд #38
Капіталовкладення задаються функцією: f (х) = 10 + 1 · t = 10 + t
Питома вага відсотка ставка i = 0,08
=
+
РІШЕННЯ
Питома вага відсотка ставка i = 0,08
=
+
РІШЕННЯ

Слайд #39
Отже, k = 30,5 млрд. руб. Це означає, що для отримання однакової нарощеної суми через 3 роки щорічні капіталовкладення від 10 до 13 млрд. руб. рівносильні одночасним початковим вкладенням 30,5 млрд. руб. при тій же, що нараховується безперервно процентній ставці.
