Презентація на тему «Парадокс близнят»
193
Слайд #1
Парадокс близнят
Слайд #2
Парадокс близнят — суперечлива на перший погляд задача з теорії відносності.
Парадокс близнят сформулював 1911 року Поль Ланжевен. Розв'язок опублікував 1918 року Альберт Ейнштейн.
Парадокс близнят сформулював 1911 року Поль Ланжевен. Розв'язок опублікував 1918 року Альберт Ейнштейн.
Слайд #3
Поль Ланжевен
Слайд #4
Альберт Ейнштейн
Слайд #5
Альберт Ейнштейн
Слайд #6
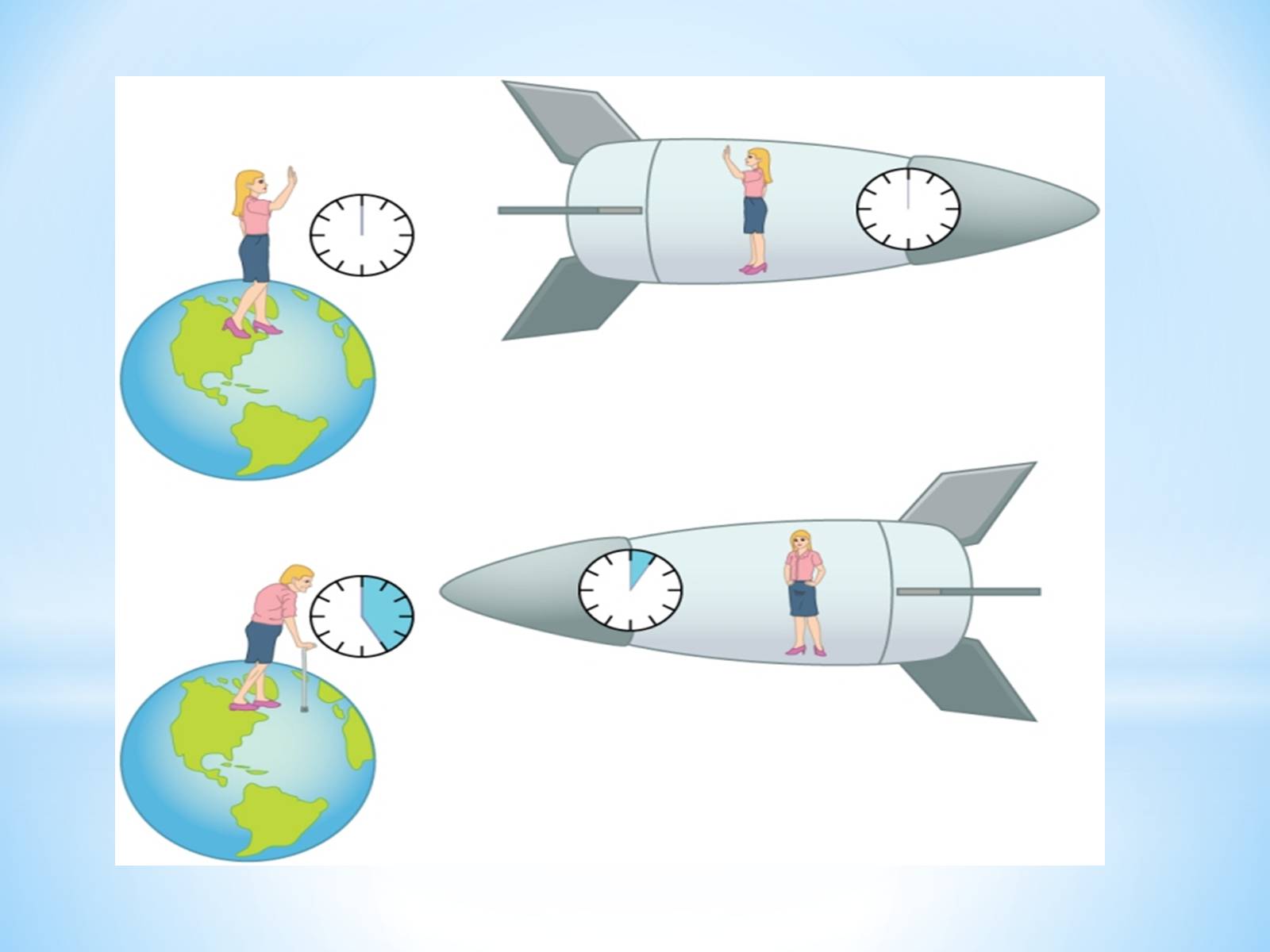
Один із двох близнюків вирушає в космічну подорож до далекої зірки, рухаючись зі швидкістю, близькою до швидкості світла, а потім повертається. Завдяки тому, що час у пов'язаній із космічним кораблем системі відліку йде повільніше, ніж у системі, пов'язаній із Землею, то його брат постарів набагато більше, ніж він сам. Справді, час у системі корабля визначається формулою
Слайд #7
Один із двох близнюків вирушає в космічну подорож до далекої зірки, рухаючись зі швидкістю, близькою до швидкості світла, а потім повертається. Завдяки тому, що час у пов'язаній із космічним кораблем системі відліку йде повільніше, ніж у системі, пов'язаній із Землею, то його брат постарів набагато більше, ніж він сам. Справді, час у системі корабля визначається формулою
Слайд #8
З іншого боку, він може вважати, що залишався непорушним, а Земля спочатку віддалилася від нього, а потім повернулася. Тоді, з його погляду, саме його брат здійснив мандрівку майже зі світловою швидкістю, а, отже, саме його брат повинен залишитися набагато молодшим.
Слайд #9
З іншого боку, він може вважати, що залишався непорушним, а Земля спочатку віддалилася від нього, а потім повернулася. Тоді, з його погляду, саме його брат здійснив мандрівку майже зі світловою швидкістю, а, отже, саме його брат повинен залишитися набагато молодшим.
Слайд #10
У межах спеціальної теорії відносності (СТВ) розв'язати парадокс неможливо. Проте парадокс знаходить своє пояснення у межах загальної теорії відносності (ЗТВ). Слід врахувати, що тільки один з братів рухався з прискоренням, а, отже, ситуація не симетрична. Саме він і має залишитися молодшим свого брата, який перебував у інерційній системі відліку.
Слайд #11
У межах спеціальної теорії відносності (СТВ) розв'язати парадокс неможливо. Проте парадокс знаходить своє пояснення у межах загальної теорії відносності (ЗТВ). Слід врахувати, що тільки один з братів рухався з прискоренням, а, отже, ситуація не симетрична. Саме він і має залишитися молодшим свого брата, який перебував у інерційній системі відліку.
Слайд #12
Перший експеримент, що мав підтвертити відповідний ефект, було поставлено 1971 року[3][4]. В межах похибки вимірів передбачення ЗТВ було підтверджено. Подібні експерименти (із дедалі вищою точністю) також підтвердили правильність розрахунків (із точністю 0,01%).
Слайд #13
Перший експеримент, що мав підтвертити відповідний ефект, було поставлено 1971 року[3][4]. В межах похибки вимірів передбачення ЗТВ було підтверджено. Подібні експерименти (із дедалі вищою точністю) також підтвердили правильність розрахунків (із точністю 0,01%).
Слайд #14
Підготувала: учнениця 9-Б класу
Пилипенко Тетяна
Вчителю: Лисяк
Тетяні Іванівні
Буча
2015
Пилипенко Тетяна
Вчителю: Лисяк
Тетяні Іванівні
Буча
2015
