- Головна
- Готові шкільні презентації
- Презентація на тему «Паралельне проектування та його властивості» (варіант 2)
Презентація на тему «Паралельне проектування та його властивості» (варіант 2)
324
Слайд #1
Паралельне проектування та його властивості
Презинтація Дегтяра Дитра учня 302 групи
Презинтація Дегтяра Дитра учня 302 групи

Слайд #2
Нехай дано площину і пряма l яка перетинає (мал.).
l
А
l1
А1
Візьмемо довільну точку А1, через і. проведемо пряму l1, паралельну прямій l.
Пряма l1, перетне в деякій точці А (мал.).
Утворену таким способом точку А назвемо проекцією точки А1 на площину при проектуванні паралельно прямій l (коротше, точка А - паралельна проекція точки А1).
введення нових понять
l
А
l1
А1
Візьмемо довільну точку А1, через і. проведемо пряму l1, паралельну прямій l.
Пряма l1, перетне в деякій точці А (мал.).
Утворену таким способом точку А назвемо проекцією точки А1 на площину при проектуванні паралельно прямій l (коротше, точка А - паралельна проекція точки А1).
введення нових понять

Слайд #3
мал. 41
Означення
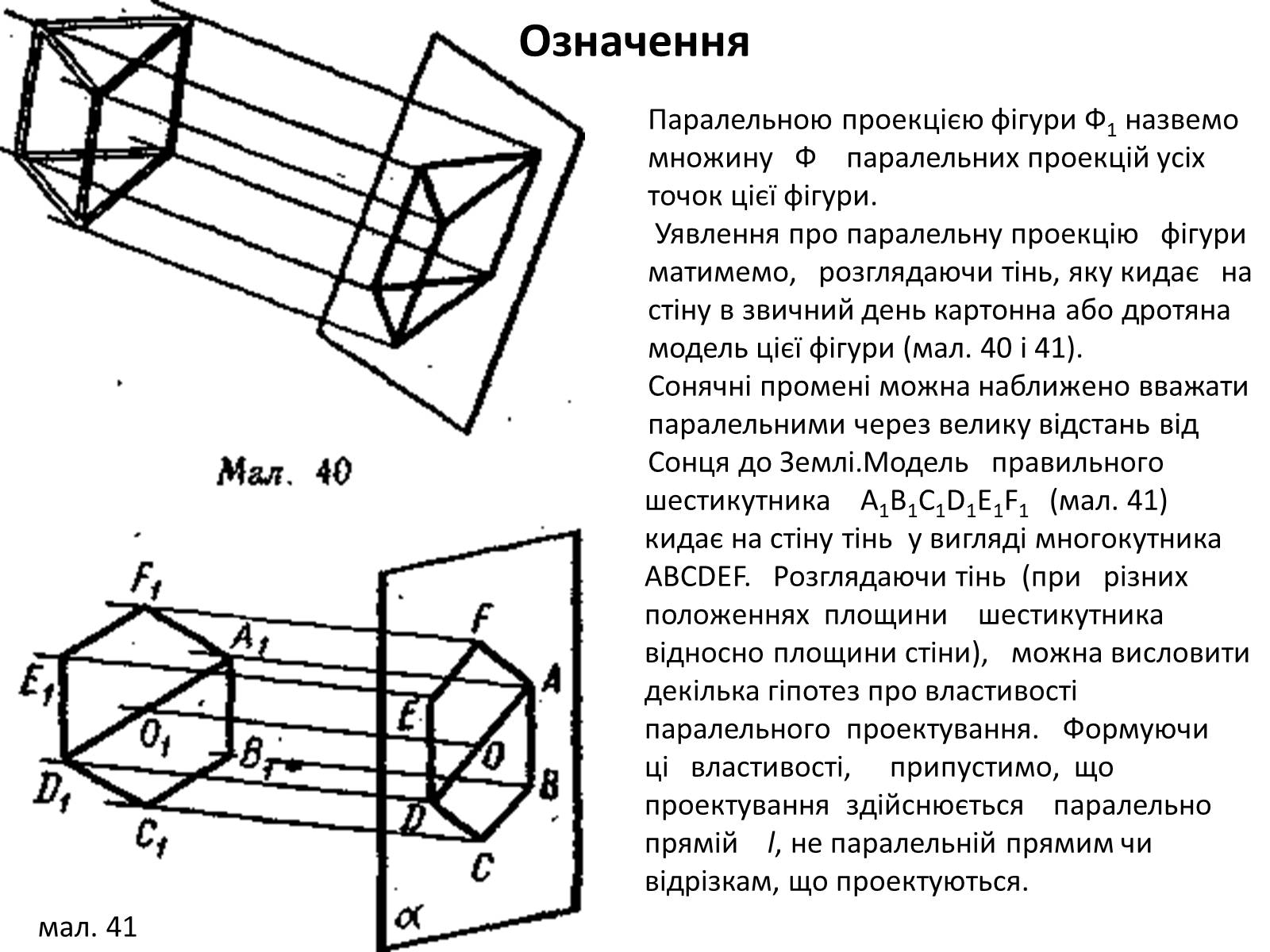
Паралельною проекцією фігури Ф1 назвемо множину Ф паралельних проекцій усіх точок цієї фігури. Уявлення про паралельну проекцію фігури матимемо, розглядаючи тінь, яку кидає на стіну в звичний день картонна або дротяна модель цієї фігури (мал. 40 і 41).Сонячні промені можна наближено вважати паралельними через велику відстань від Сонця до Землі.
Модель правильного шестикутника А1В1С1D1E1F1 (мал. 41) кидає на стіну тінь у вигляді многокутника АВСDЕF. Розглядаючи тінь (при різних положеннях площини шестикутника відносно площини стіни), можна висловити декілька гіпотез про властивості паралельного проектування. Формуючи ці властивості, припустимо, що проектування здійснюється паралельно прямій l, не паралельній прямим чи відрізкам, що проектуються.
Означення
Паралельною проекцією фігури Ф1 назвемо множину Ф паралельних проекцій усіх точок цієї фігури. Уявлення про паралельну проекцію фігури матимемо, розглядаючи тінь, яку кидає на стіну в звичний день картонна або дротяна модель цієї фігури (мал. 40 і 41).Сонячні промені можна наближено вважати паралельними через велику відстань від Сонця до Землі.
Модель правильного шестикутника А1В1С1D1E1F1 (мал. 41) кидає на стіну тінь у вигляді многокутника АВСDЕF. Розглядаючи тінь (при різних положеннях площини шестикутника відносно площини стіни), можна висловити декілька гіпотез про властивості паралельного проектування. Формуючи ці властивості, припустимо, що проектування здійснюється паралельно прямій l, не паралельній прямим чи відрізкам, що проектуються.
Слайд #4
Властивості
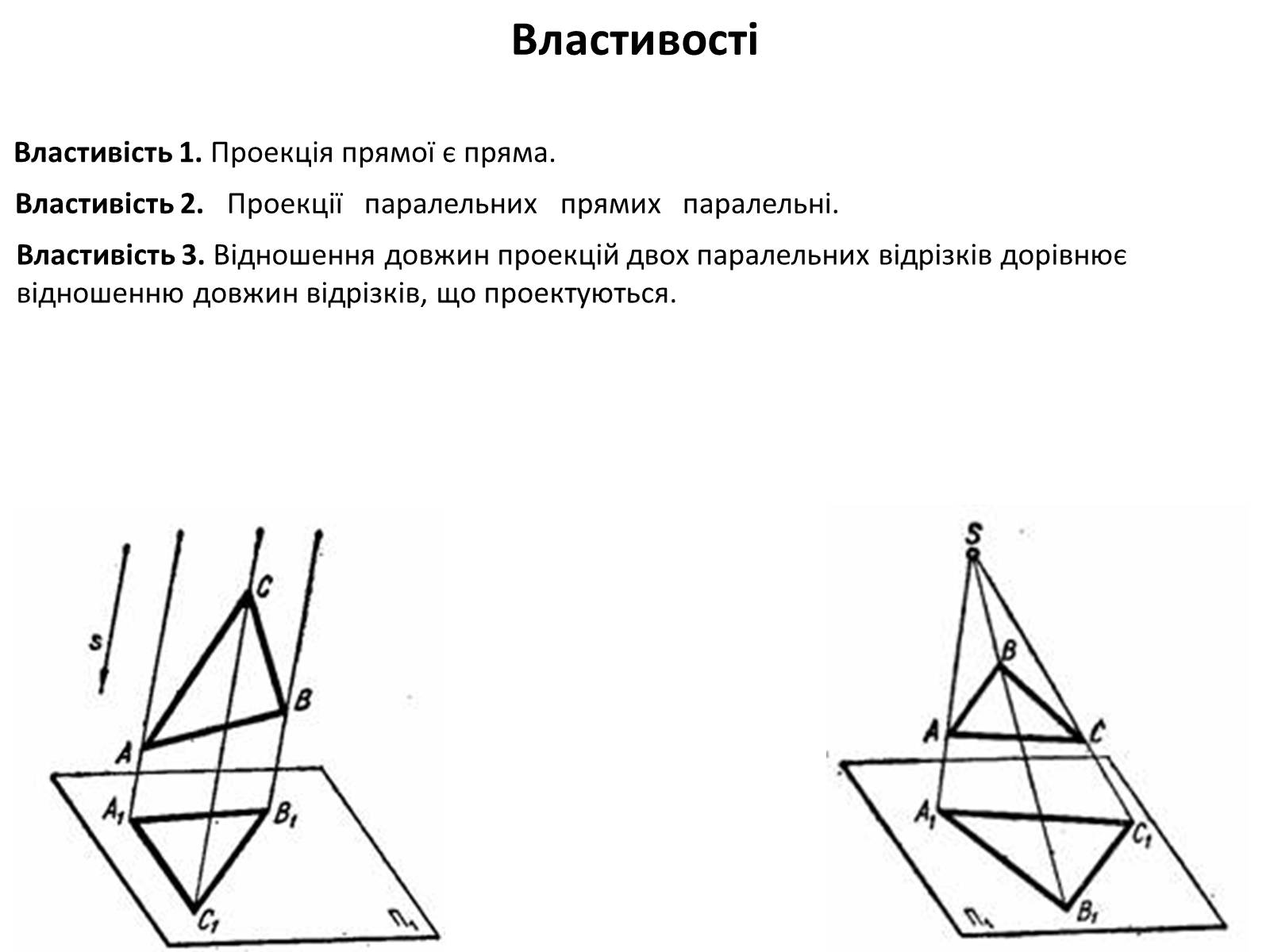
Властивість 1. Проекція прямої є пряма.
Властивість 2. Проекції паралельних прямих паралельні.
Властивість 3. Відношення довжин проекцій двох паралельних відрізків дорівнює відношенню довжин відрізків, що проектуються.
Властивість 1. Проекція прямої є пряма.
Властивість 2. Проекції паралельних прямих паралельні.
Властивість 3. Відношення довжин проекцій двох паралельних відрізків дорівнює відношенню довжин відрізків, що проектуються.
Слайд #5
Властивості зображення просторових фігур на площині
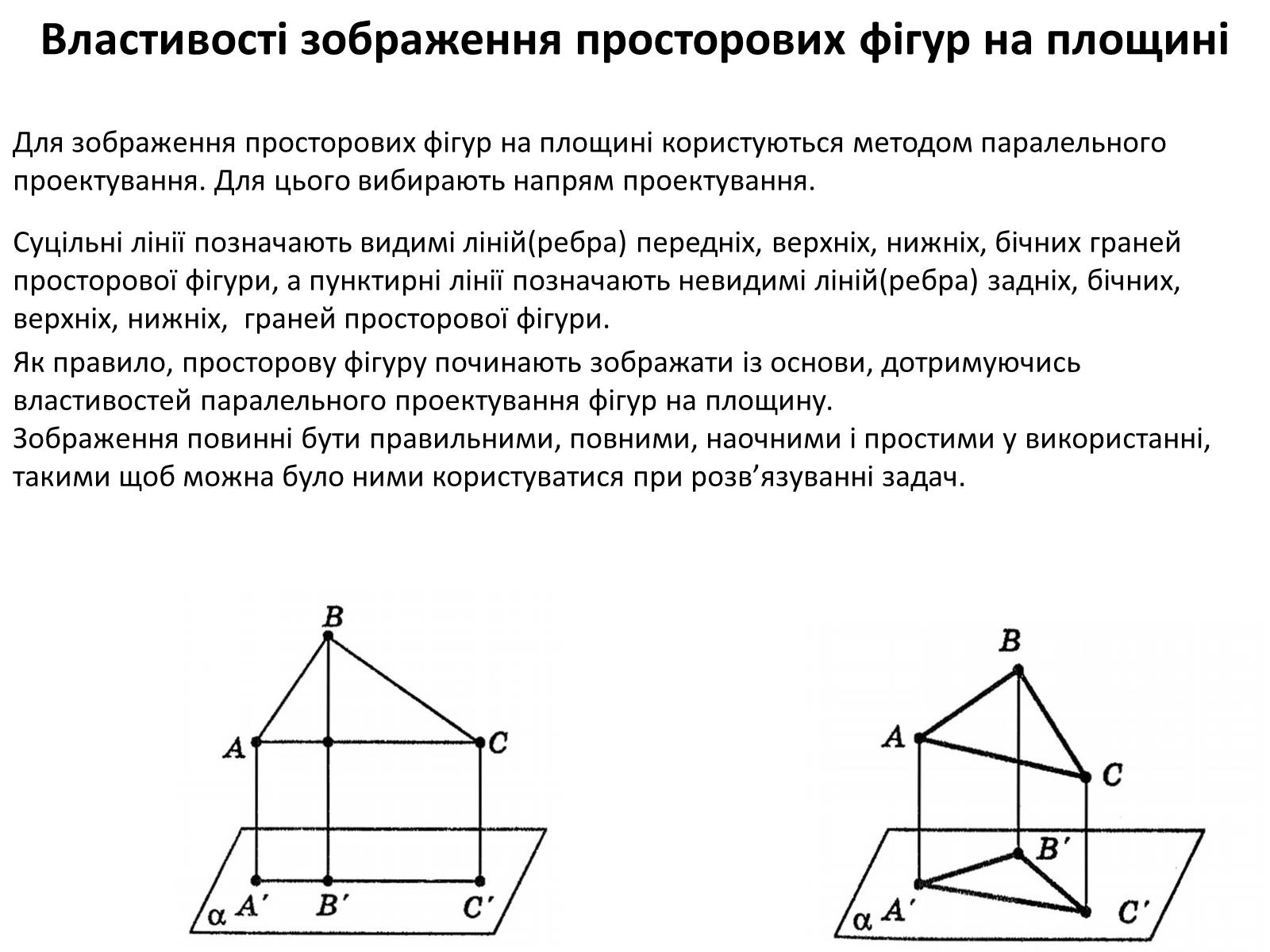
Для зображення просторових фігур на площині користуються методом паралельного проектування. Для цього вибирають напрям проектування.
Суцільні лінії позначають видимі ліній(ребра) передніх, верхніх, нижніх, бічних граней просторової фігури, а пунктирні лінії позначають невидимі ліній(ребра) задніх, бічних, верхніх, нижніх, граней просторової фігури.
Як правило, просторову фігуру починають зображати із основи, дотримуючись властивостей паралельного проектування фігур на площину.
Зображення повинні бути правильними, повними, наочними і простими у використанні, такими щоб можна було ними користуватися при розв'язуванні задач.
Для зображення просторових фігур на площині користуються методом паралельного проектування. Для цього вибирають напрям проектування.
Суцільні лінії позначають видимі ліній(ребра) передніх, верхніх, нижніх, бічних граней просторової фігури, а пунктирні лінії позначають невидимі ліній(ребра) задніх, бічних, верхніх, нижніх, граней просторової фігури.
Як правило, просторову фігуру починають зображати із основи, дотримуючись властивостей паралельного проектування фігур на площину.
Зображення повинні бути правильними, повними, наочними і простими у використанні, такими щоб можна було ними користуватися при розв'язуванні задач.
Слайд #6
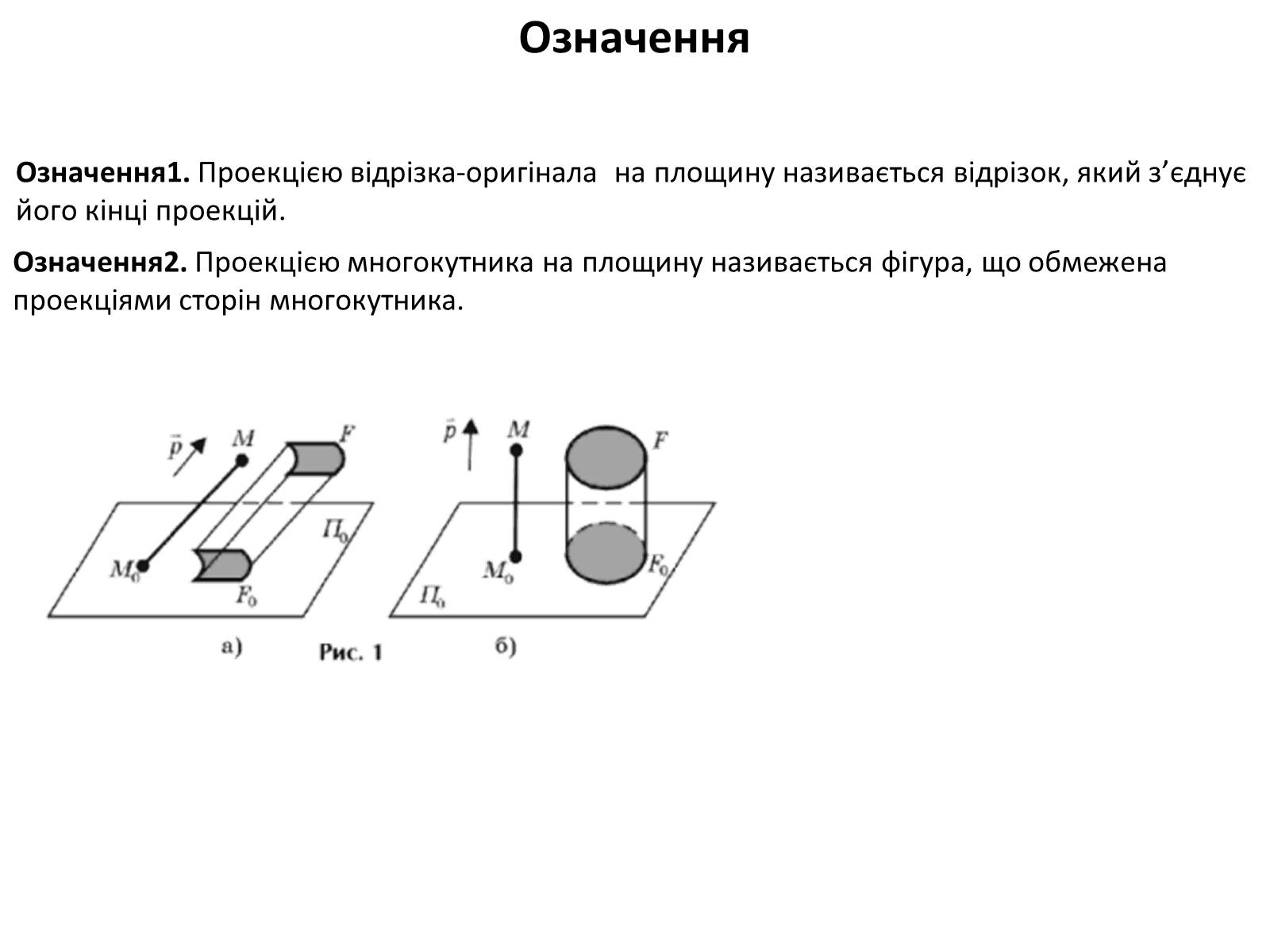
Означення1. Проекцією відрізка-оригінала на площину називається відрізок, який з'єднує його кінці проекцій.
Означення
Означення2. Проекцією многокутника на площину називається фігура, що обмежена проекціями сторін многокутника.
Означення
Означення2. Проекцією многокутника на площину називається фігура, що обмежена проекціями сторін многокутника.
Слайд #7
Властивості
Властивість. Відрізок, що не паралельний напряму проектування на площину креслення, проектується у відрізок, при цьому довжина спроектованого відрізка може не дорівнювати довжині даного відрізка.
Властивість. При паралельному проектуванні на площину паралельність відрізків зберігається.
Властивість. При паралельному проектуванні на площину двох відрізків, що перетинаються(або непаралельні), не зберігається відношення довжин даних відрізків.
Властивість. При паралельному проектуванні на площину відношення відрізків однієї прямої або паралельних відрізків зберігається. Зокрема, середина заданого відрізка проектується в середину його проекції.
Властивість. При паралельному проектуванні на площину паралельні прямі проектуються в паралельні прямі.
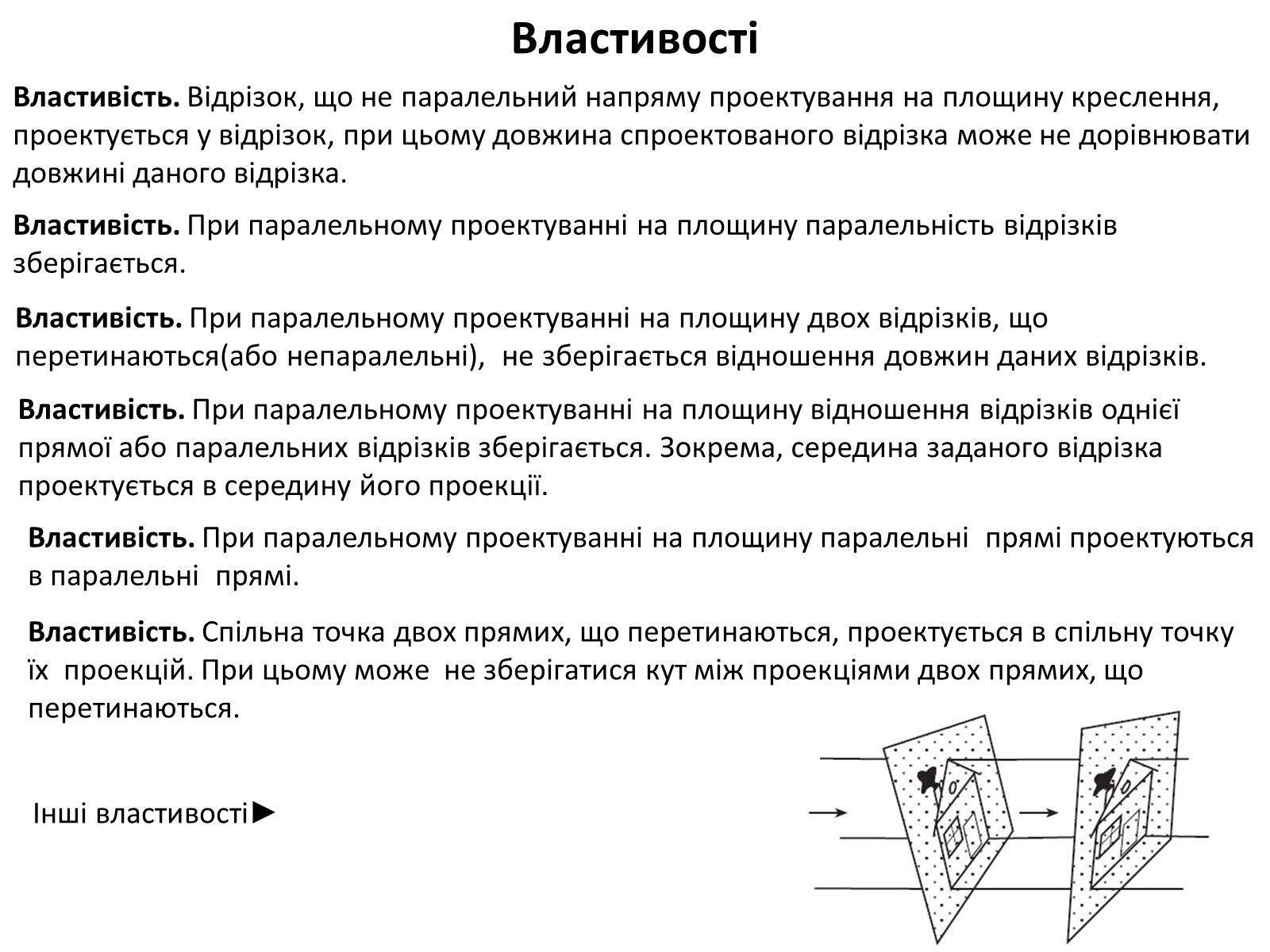
Властивість. Спільна точка двох прямих, що перетинаються, проектується в спільну точку їх проекцій. При цьому може не зберігатися кут між проекціями двох прямих, що перетинаються.
Інші властивості►
Властивість. Відрізок, що не паралельний напряму проектування на площину креслення, проектується у відрізок, при цьому довжина спроектованого відрізка може не дорівнювати довжині даного відрізка.
Властивість. При паралельному проектуванні на площину паралельність відрізків зберігається.
Властивість. При паралельному проектуванні на площину двох відрізків, що перетинаються(або непаралельні), не зберігається відношення довжин даних відрізків.
Властивість. При паралельному проектуванні на площину відношення відрізків однієї прямої або паралельних відрізків зберігається. Зокрема, середина заданого відрізка проектується в середину його проекції.
Властивість. При паралельному проектуванні на площину паралельні прямі проектуються в паралельні прямі.
Властивість. Спільна точка двох прямих, що перетинаються, проектується в спільну точку їх проекцій. При цьому може не зберігатися кут між проекціями двох прямих, що перетинаються.
Інші властивості►
Слайд #8
Властивість. Спільна точка двох прямих, що перетинаються, проектується в спільну точку їх проекцій. При цьому може не зберігатися кут між проекціями двох прямих, що перетинаються.
Властивість. При паралельному проектуванні на площину будь-який трикутник(прямокутний, рівнобедрений, правильний), що не паралельний напряму проектування, має своєю проекцією довільний трикутник(не обов'язково того ж виду). Зображення трикутника робиться у зручному розташуванні.
Якщо трикутник АВС – прямокутний, то зображення напрямків двох його висот (катетів) задано. Довільно зображуються висота, опущена на гіпотенузу і центр вписаного кола. Зображення перпендикуляра, опущеного із заданої точки гіпотенузи на будь-який катет, є відрізком, що паралельний другому катету.
Якщо трикутник АВС – рівнобедрений, то зображення на площині медіани ВМ проекції є зображенням висоти, бісектриси, що проведені до основи даного трикутника. Зображення центра вписаного і описаного кіл належать відрізку ВМ.
Якщо трикутник АВС – рівносторонній, то центри вписаного і описаного кіл співпадають і лежать в точці перетину медіан. Тому побудова зображення цього трикутника не може бути довільним. Точка перетину висот і бісектрис правильного трикутника проектується в точку перетину медіан проекції.
Властивість. Точка перетину медіан трикутника проектується в точку перетину медіан проекції.
Властивість. При паралельному проектуванні на площину будь-який паралелограм(квадрат, ромб, прямокутник), що не паралельний напряму проектування, має своєю проекцією довільний паралелограм(не обов'язково того ж виду).
На зображенні довільного паралелограма зображення його висот, проведених із однієї вершини, можна побудувати довільно. До того ж висоти, проведені з вершин гострого кута паралелограма оригінала лежать поза межами проекції, а висоти, проведені із тупого кута лежать всередині проекції.
Якщо АСВD – ромб, то на зображенні визначається пара взаємно перпендикулярних прямих – це діагоналі ромба АСВD. Тому довільно можна побудувати зображення лише однієї висоти з даної вершини ромба на його сторону. При зображенні другої висоти ромба враховують, що основи цих висот лежать на прямій, паралельній діагоналі ромба. Аналогічно зображуються перпендикуляри, опущені на сторони ромба з будь-якої точки його діагоналі.
Якщо АСВD – квадрат, то його зображення є довільним паралелограм, до того ж зображення висот, бісектрис, кутів, перпендикулярів до сторін будувати довільно не можна.
Властивість. При паралельному проектуванні на площину будь-яка трапеція, що не паралельна напряму проектування, має своєю проекцією довільну трапецію (не обов'язково того ж виду).
Властивість. При паралельному проектуванні на площину будь-яке коло, що не паралельне напряму проектування, має своєю проекцією довільний еліпс. Центром кола на зображенні є точка перетину спряжених діаметрів еліпса. Два діаметри кола(еліпса) називаються спряженими, якщо кожний з них поділяє навпіл всі хорди, паралельні другому діаметру.
Властивість. При паралельному проектуванні на площину будь-який трикутник(прямокутний, рівнобедрений, правильний), що не паралельний напряму проектування, має своєю проекцією довільний трикутник(не обов'язково того ж виду). Зображення трикутника робиться у зручному розташуванні.
Якщо трикутник АВС – прямокутний, то зображення напрямків двох його висот (катетів) задано. Довільно зображуються висота, опущена на гіпотенузу і центр вписаного кола. Зображення перпендикуляра, опущеного із заданої точки гіпотенузи на будь-який катет, є відрізком, що паралельний другому катету.
Якщо трикутник АВС – рівнобедрений, то зображення на площині медіани ВМ проекції є зображенням висоти, бісектриси, що проведені до основи даного трикутника. Зображення центра вписаного і описаного кіл належать відрізку ВМ.
Якщо трикутник АВС – рівносторонній, то центри вписаного і описаного кіл співпадають і лежать в точці перетину медіан. Тому побудова зображення цього трикутника не може бути довільним. Точка перетину висот і бісектрис правильного трикутника проектується в точку перетину медіан проекції.
Властивість. Точка перетину медіан трикутника проектується в точку перетину медіан проекції.
Властивість. При паралельному проектуванні на площину будь-який паралелограм(квадрат, ромб, прямокутник), що не паралельний напряму проектування, має своєю проекцією довільний паралелограм(не обов'язково того ж виду).
На зображенні довільного паралелограма зображення його висот, проведених із однієї вершини, можна побудувати довільно. До того ж висоти, проведені з вершин гострого кута паралелограма оригінала лежать поза межами проекції, а висоти, проведені із тупого кута лежать всередині проекції.
Якщо АСВD – ромб, то на зображенні визначається пара взаємно перпендикулярних прямих – це діагоналі ромба АСВD. Тому довільно можна побудувати зображення лише однієї висоти з даної вершини ромба на його сторону. При зображенні другої висоти ромба враховують, що основи цих висот лежать на прямій, паралельній діагоналі ромба. Аналогічно зображуються перпендикуляри, опущені на сторони ромба з будь-якої точки його діагоналі.
Якщо АСВD – квадрат, то його зображення є довільним паралелограм, до того ж зображення висот, бісектрис, кутів, перпендикулярів до сторін будувати довільно не можна.
Властивість. При паралельному проектуванні на площину будь-яка трапеція, що не паралельна напряму проектування, має своєю проекцією довільну трапецію (не обов'язково того ж виду).
Властивість. При паралельному проектуванні на площину будь-яке коло, що не паралельне напряму проектування, має своєю проекцією довільний еліпс. Центром кола на зображенні є точка перетину спряжених діаметрів еліпса. Два діаметри кола(еліпса) називаються спряженими, якщо кожний з них поділяє навпіл всі хорди, паралельні другому діаметру.

Слайд #9
Презентація учня 302 групи Дегтяра Дмитра
